数据结构-图-最小生成树问题
最小生成树
- 并查集
- 定义
- 举例说明
- 查找某个元素属于哪个集合
- 代码实现
- 路径压缩
- Kruskal
- 算法原理
- 代码实现
- Prim
- 算法原理
- 代码实现
并查集
定义
🚀在一些应用问题中,需要将n个不同的元素分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中,要反复用到查询某一个元素属于哪个集合的运算。适合描述这类问题的抽象数据结构叫做并查集。
🚀由于每个集合就是一颗树形结构,一个并查集内存在多个集合,所以并查集是一个森林。
🚀通常用数组来充当这种数据结构,采用双亲表示法的方式,即子节点存储父节点的指针。
举例说明
🚀例如,有10名同学,它们的编号分别为0-9,它们来自三个班级(1班,2班,3班),其中0,3,4号同学来自一班,1,7,9同学来自2班,2,5,6,8号同学来自3班。
初始结构:每个元素各自独立为一个集合。
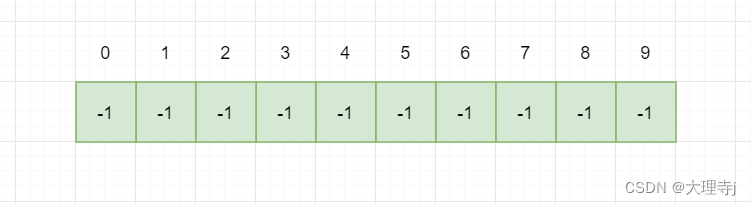
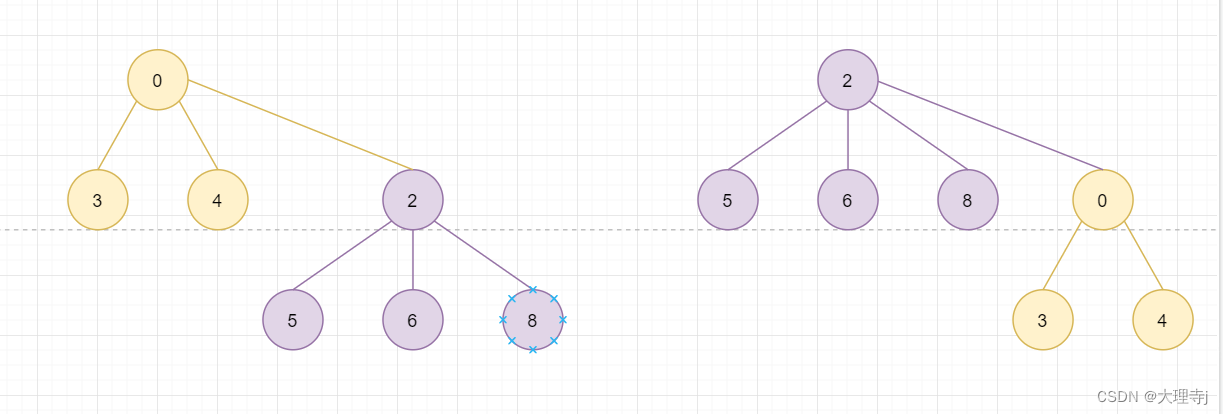
元素的合并:相同班级的同学合并为同一个集合。
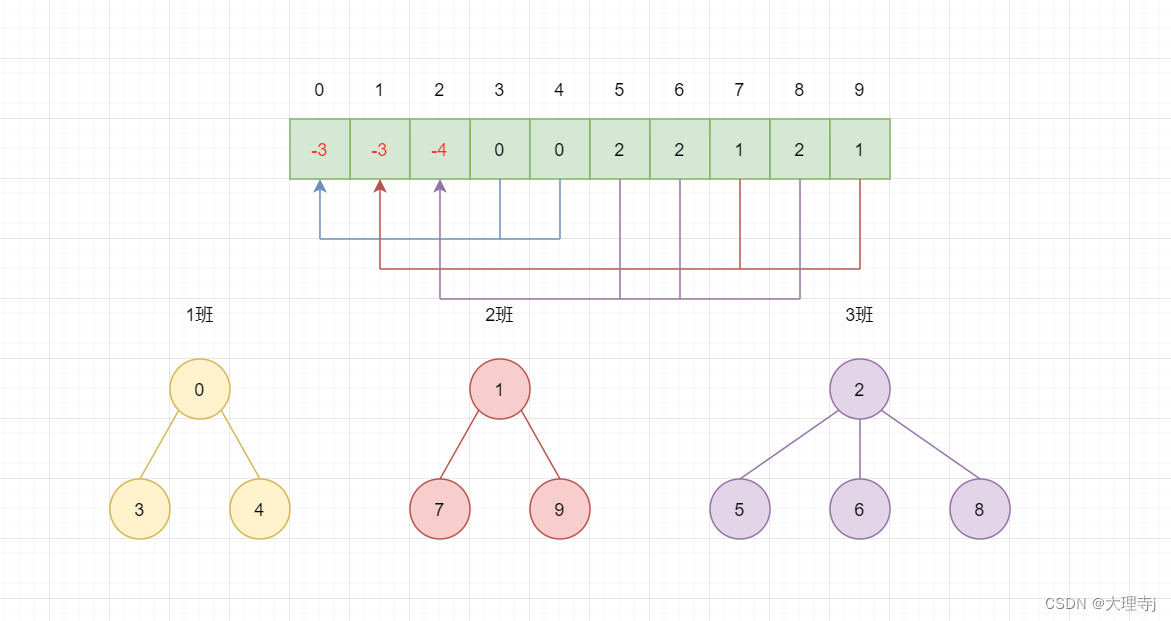
🚀合并规则:
将子节点的数据加到父节点的数据中,将字节点的数据改为父节点的指针。这样父节点中的数据的绝对值就是此集合中元素个数,各个子节点存储的都是指向父节点的指针。
🚀合并的优化:
在合并时,最好将集合内元素数量较少的集合合并到集合内元素数量多的集合。这样在查找某个元素属于哪个集合时可以减少时间消耗。例如,将1班和3班合并,优先是将1班合并到3班,这样第三层的结点数量比较少,相比于将3班合并到1班。
查找某个元素属于哪个集合
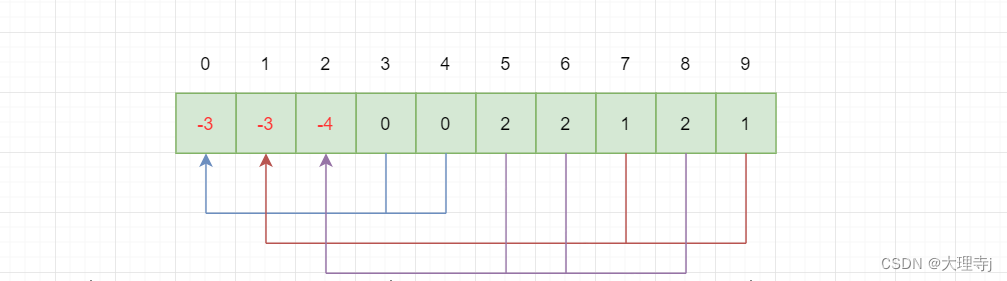
🚀例如查找n号下元素属于哪个集合,只需要判断n号位置的元素是否为负数,如果为负数说明n号位置就是这个集合的根节点(用根节点的下标来标识集合),如果不是负数就顺着父节点向上访问,直到根节点为止。
代码实现
#pragma once#include <vector>
#include <iostream>/*
* 并查集
* 1.核心采用双亲表示法,孩子结点存储的是父节点的下表
* 2.采用类似堆的结构表示---在数组中存储
*/
class UnionFindSet {
private:std::vector<int> _ufs;
public:UnionFindSet(size_t n) :_ufs(n,-1) {}int FindRoot(int x) {int parent = x;//一直向上找到存储负数的结点while (_ufs[parent] >= 0) {parent = _ufs[parent];}return parent;}void Union(int x1, int x2) {int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 == root2) { return; } //本身就在一个集合当中if (abs(_ufs[root1]) < abs(_ufs[root2])) {std::swap(root1, root2);}_ufs[root1] += _ufs[root2]; //将root2结点的数据加到root1结点的数据上_ufs[root2] = root1; //将root2结点的数据修改为root1(根结点的下标)}size_t SetSize() const {size_t cnt = 0;for (auto& e : _ufs) {if (e < 0) { cnt++; } //结点数据为0的就表示为根结点,能够代表一个集合}return cnt;}bool InSet(int x1, int x2) {int root1 = FindRoot(x1);int root2 = FindRoot(x2);return root1 == root2;}
};
路径压缩
🚀在经过多次集合合并时,可能会出现某个集合的树形结构深度很深,从而导致查询某个元素的集合时时间消耗比较大,所以可以对树形结构的路径进行压缩。
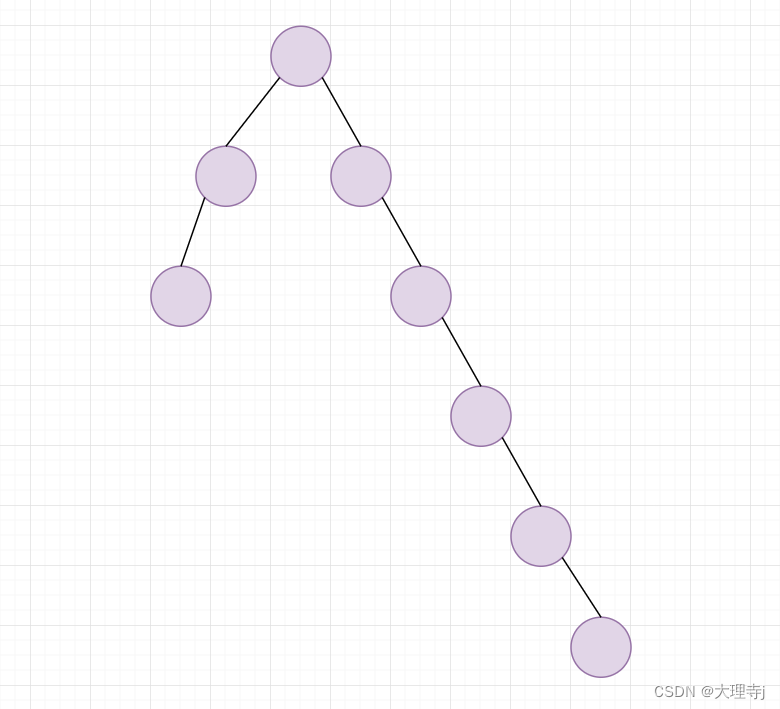
上图只是个示例,通常来说数据量很大的时候才需要路径压缩。
压缩策略:
在查找某个元素属于哪个集合时进行路径的压缩,在找到某个元素的根节点后不着急返回,而是依次将此路径上的该元素的父节点合并到根结点处,完成路径压缩。这样下次再查找某个元素属于哪个集合时,就可以提高效率。
int FindRoot(int x) {int parent = x;//一直向上找到存储负数的结点while (_ufs[parent] >= 0) {parent = _ufs[parent];}//核心代码int cur = x;while (_ufs[cur] >= 0) {int tmp = cur;cur = _ufs[cur];_ufs[tmp] = parent;}return parent;
}
Kruskal
最小生成树
🚀最小生成树就是在图的所有生成树中找出各个路径权值和最小的那个路径。
算法原理
🚀克鲁斯卡尔算法是求图的最小生成树的一个经典算法,其采用全局贪心的思想,每次都去选权值最小的边(可以将所有边放在一个小根堆中每次获取堆顶元素)去构成最小生成树(不能重复选取某一个边),但是这种贪心方式可能会造成环路的产生,所以在每选一个边之前都要判断一下选取这个边后会不会构成环路。而判环的这个步骤使用并查集是非常适合的,可以将已经选取出来的构成最小生成树的顶点放在一个集合S中,在添加某个边时,如果这个边的两个顶点均位于集合S中,说明构成了环路这条边是不能选取的。
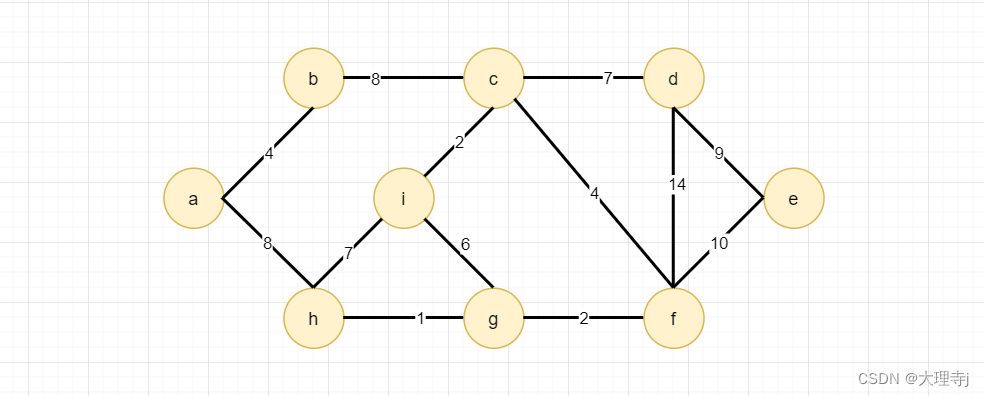
选取边的过程:
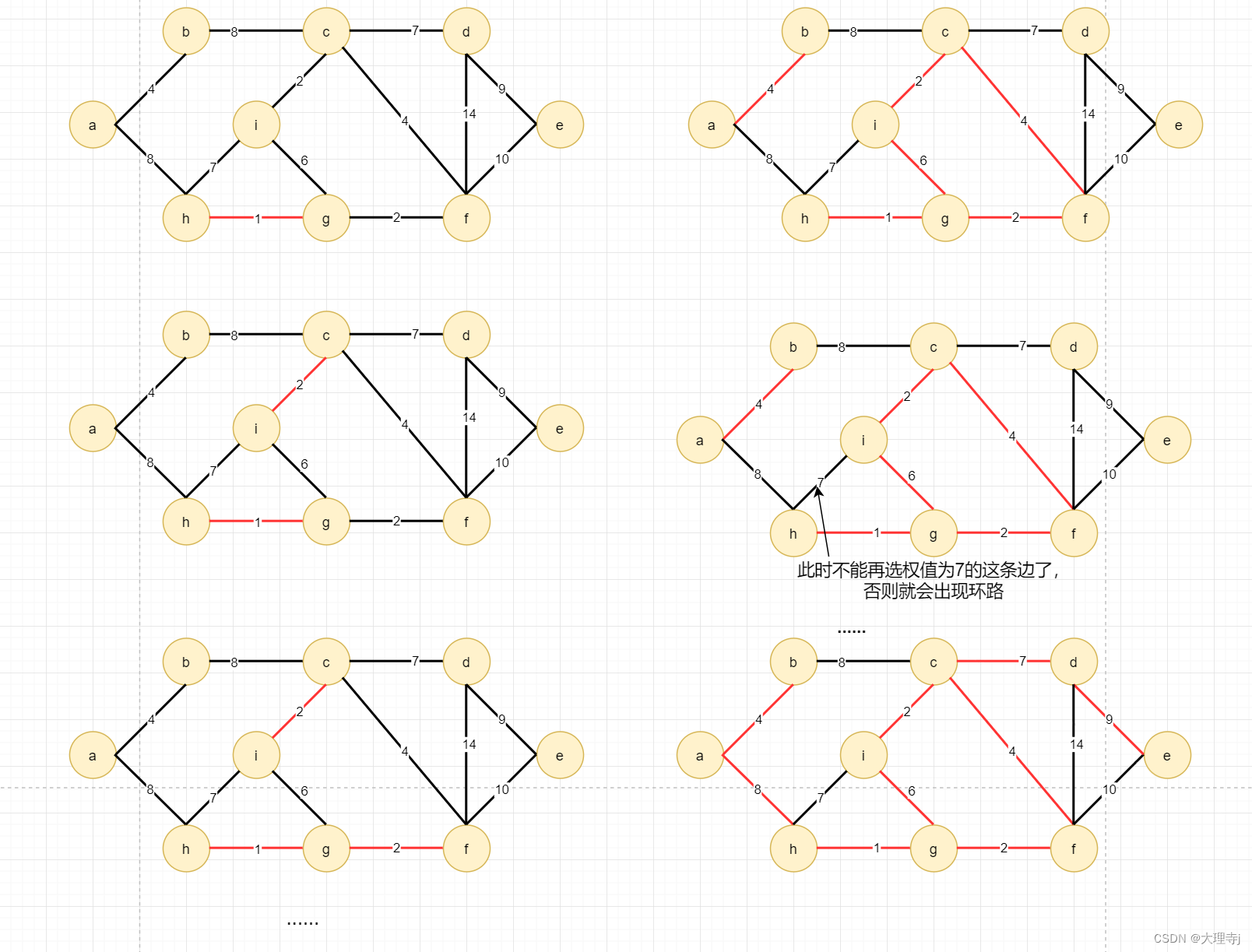
🚀最小生成树的结果并不唯一,例如上图中有两个权值为8的边,上面的选法中是选取了ah这条边,选取bc这条边也是没有问题的。
代码实现
struct Edge {size_t _srci;size_t _dsti;W _weight;Edge(size_t srci,size_t dsti,const W& weight) :_srci(srci),_dsti(dsti),_weight(weight) {}bool operator > (const Edge& e) const {return _weight > e._weight;}
};W Kruskal(self& min_tree) {size_t n = _vertex.size();min_tree._vertex = _vertex;min_tree._index_map = _index_map;//初始化矩阵min_tree._matrix.resize(n, std::vector<W>(n, W_MAX));//开始计算最小生成树std::priority_queue<Edge,std::vector<Edge>,std::greater<Edge>> pq;for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (i < j && _matrix[i][j] != W_MAX) { //i<j在无向图中避免同一条边添加两次pq.push(Edge(i, j, _matrix[i][j]));}}}W total = W();//记录权值和size_t size = 0;//记录挑选出的边的个数UnionFindSet ufs(n);while (size < n - 1 && !pq.empty()) {Edge eg = pq.top();pq.pop();if (ufs.InSet(eg._srci, eg._dsti) == false) {min_tree._AddEdge(eg._srci, eg._dsti, eg._weight);ufs.Union((int)eg._srci, (int)eg._dsti);total += eg._weight;++size;}}if (size != n - 1) {return W();}return total;
}
Prim
算法原理
🚀Prim算法与Krunskal算法都是采用贪心的策略,但是Prim算法采用的是局部贪心的策略,在Prim算法中会将图的顶点分类到两个集合X,Y中,对于已经选入到最小生成树的边相连的顶点放在X集合中,没有选进最小生成树的顶点放入Y集合。而在贪心选取权值最小的边时,是在一个顶点位于X集合另一个顶点位于Y集合的所有边中去选择的。所以Prim算法需要指定一个起始顶点。当某个顶点被添加到X集合后,要将与其相连的边放入到优先级队列中,放入优先级队列的边也是有要求的就是它另一个顶点必须是在Y集合中的(如果采用优先级队列的方式存储边,仍然会出现环路情况,所以在选边的同时也要注意判环操作)
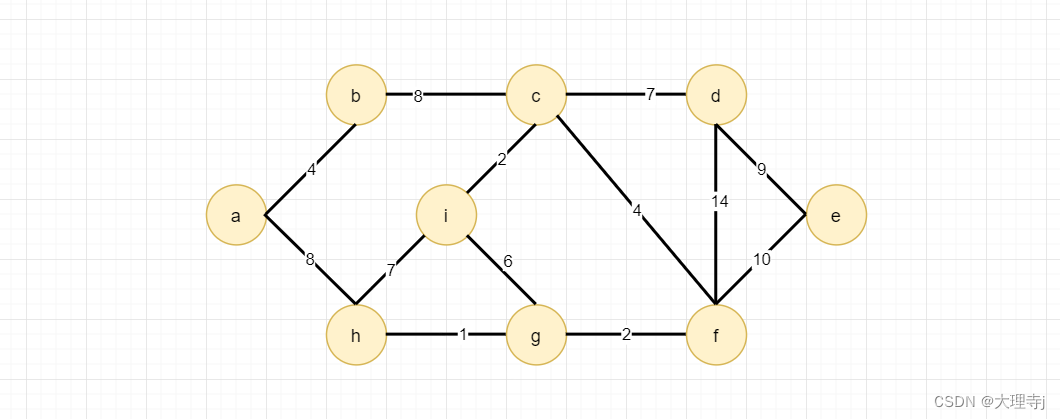
选取边的过程
假设起始顶点为a:
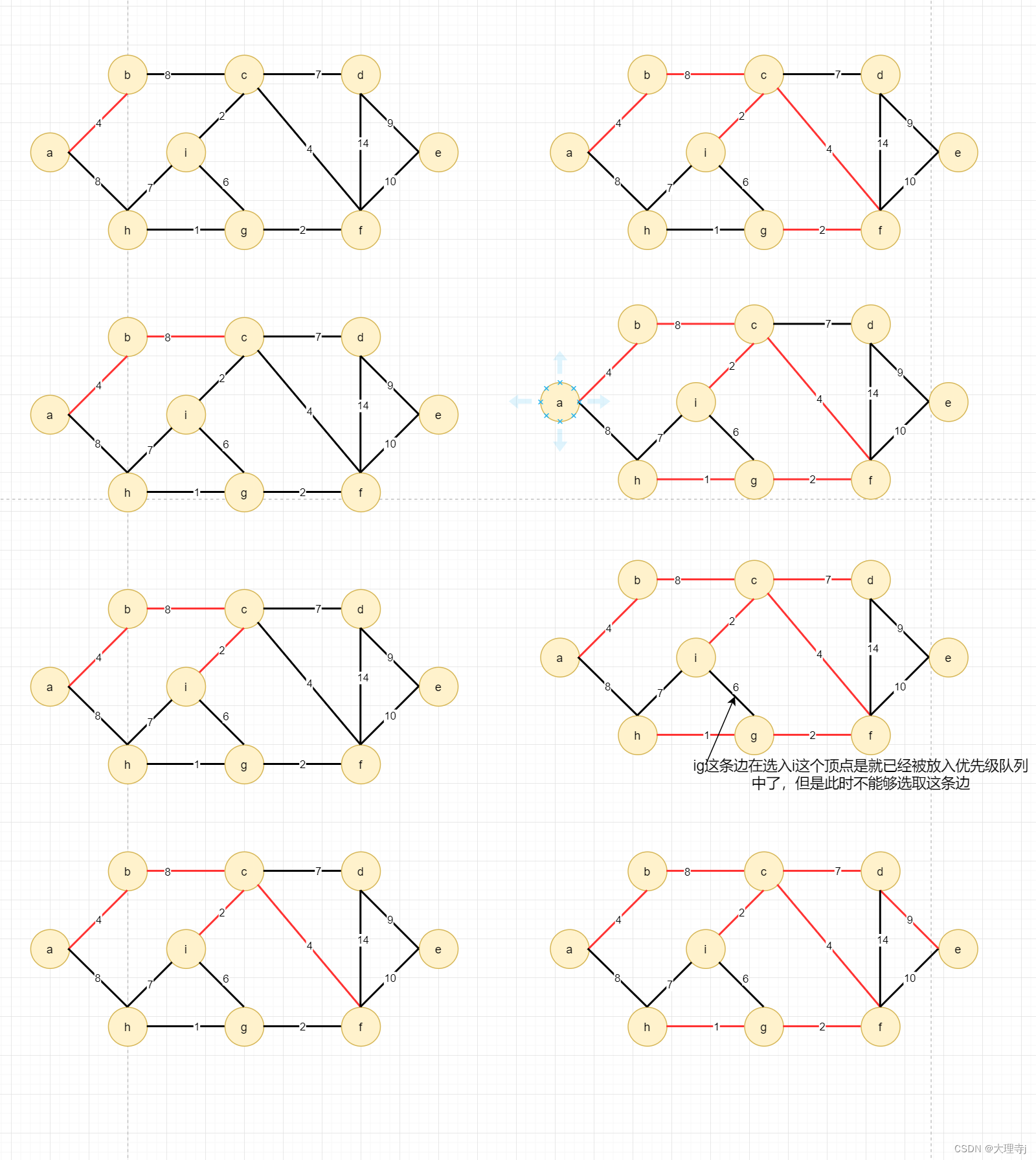
代码实现
W Prim(self& min_tree, const V& src) {size_t n = _vertex.size();min_tree._vertex = _vertex;min_tree._index_map = _index_map;//初始化矩阵min_tree._matrix.resize(n, std::vector<W>(n, W_MAX));//将所有的顶点划分为两个集合 X Y,已经选择的点放入X集合中,没有选择的点在Y集合中size_t srci = this->GetVertexIndex(src);std::vector<bool> X(n, false);std::vector<bool> Y(n, true);X[srci] = true;Y[srci] = false;//将与X集合中所有顶点相连的边存入优先级队列,以供贪心选择std::priority_queue<Edge, std::vector<Edge>, std::greater<Edge>> pq;for (size_t i = 0; i < n; ++i) {if (_matrix[srci][i] != W_MAX) {pq.push(Edge(srci, i, _matrix[srci][i]));}}size_t size = 0;W total_w = W();while (size < n - 1 && !pq.empty()) {Edge eg = pq.top();pq.pop();//防止选出的边构成环if (true == X[eg._dsti]) {continue;}X[eg._dsti] = true;Y[eg._dsti] = false;min_tree._AddEdge(eg._srci, eg._dsti, eg._weight);++size;total_w += eg._weight;//std::cout << _vertex[eg._srci] << "->" << _vertex[eg._dsti] << ":" << eg._weight << std::endl;//将以dsti点为起点的边加入到队列中for (size_t i = 0; i < n; i++) {//存在边且终点位于Y集合中if (_matrix[eg._dsti][i] != W_MAX && Y[i]) {pq.push(Edge(eg._dsti, i, _matrix[eg._dsti][i]));}}}if (size != n - 1) {return W();}return total_w;
}
相关文章:

数据结构-图-最小生成树问题
最小生成树 并查集定义举例说明查找某个元素属于哪个集合代码实现路径压缩 Kruskal算法原理代码实现 Prim算法原理代码实现 并查集 定义 🚀在一些应用问题中,需要将n个不同的元素分成一些不相交的集合。开始时,每个元素自成一个单元素集合&…...
使用vite+npm封装组件库并发布到npm仓库
组件库背景:使用elementplusvue封装了一个通过表单组件。通过JSX对el-form下的el-input和el-button等表单进行统一封装,最后达到,通过数据即可一键生成页面表单的功能。 1.使用vite创建vue项目 npm create vitelatest elementplus-auto-form…...

85.最大矩形
单调栈,时间复杂度o(mn),空间复杂度o(mn) class Solution { public:int maximalRectangle(vector<vector<char>>& matrix) {int mmatrix.size();if(m0){return 0;}int nmatrix[0].size();//记录矩阵中每个元素左边连续1的数量vector<…...
Windows服务器 开机自启动服务
1、新建txt,并粘贴下面脚本 start cmd /k "cd /d D:\ahjd&&java -jar clips-admin.jar" start cmd /k "cd /d D:\ahjd\dist&&simple-http-server.exe -i -p 8000"说明,脚本格式为:start cmd /k “cd /d…...

《算法通关之路》chapter17一些通用解题模板
《算法通关之路》学习笔记,记录一下自己的刷题过程,详细的内容请大家购买作者的书籍查阅。 1 二分法 1.1 普通二分法 # 查找nums数组中元素值为target的下标。如果不存在,则返回-1def bs(nums: list[int], target: int) -> int :l, h …...
常用求解器安装
1 建模语言pyomo Pyomo是一个Python建模语言,用于数学优化建模。它可以与不同的求解器(如Gurobi,CPLEX,GLPK,SCIP等)集成使用,以求解各种数学优化问题。可以使用Pyomo建立数学优化模型…...
)
第三章:最新版零基础学习 PYTHON 教程(第一节 - Python 运算符)
在Python编程中,运算符一般用于对值和变量进行操作。这些是用于逻辑和算术运算的标准符号。在本文中,我们将研究不同类型的Python 运算符。 运算符:这些是特殊符号。例如- + 、 * 、 / 等。操作数:它是应用运算符的值。目录 Python 中的运算符类型 Python 中的算术运算符…...
细粒度特征提取和定位用于目标检测:PPCNN
1、简介 近年来,深度卷积神经网络在计算机视觉上取得了优异的性能。深度卷积神经网络以精确地分类目标信息而闻名,并采用了简单的卷积体系结构来降低图层的复杂性。基于深度卷积神经网络概念设计的VGG网络。VGGNet在对大规模图像进行分类方面取得了巨大…...

【STM32单片机】数学自动出题器设计
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用STM32F103C8T6单片机控制器,使用按键、IIC OLED模块等。 主要功能: 系统运行后,OLED液晶显示出题器开机界面,默认结果范围为100,可按…...
C语言之动态内存管理篇(1)
目录 为什么存在动态内存分配 动态内存函数的介绍 malloc free calloc realloc 常见的动态内存错误 今天收假了,抓紧时间写几篇博客。我又来赶进度了。今天我们来讲解动态内存管理。🆗🆗 为什么存在动态内存分配 假设我们去实现一个…...
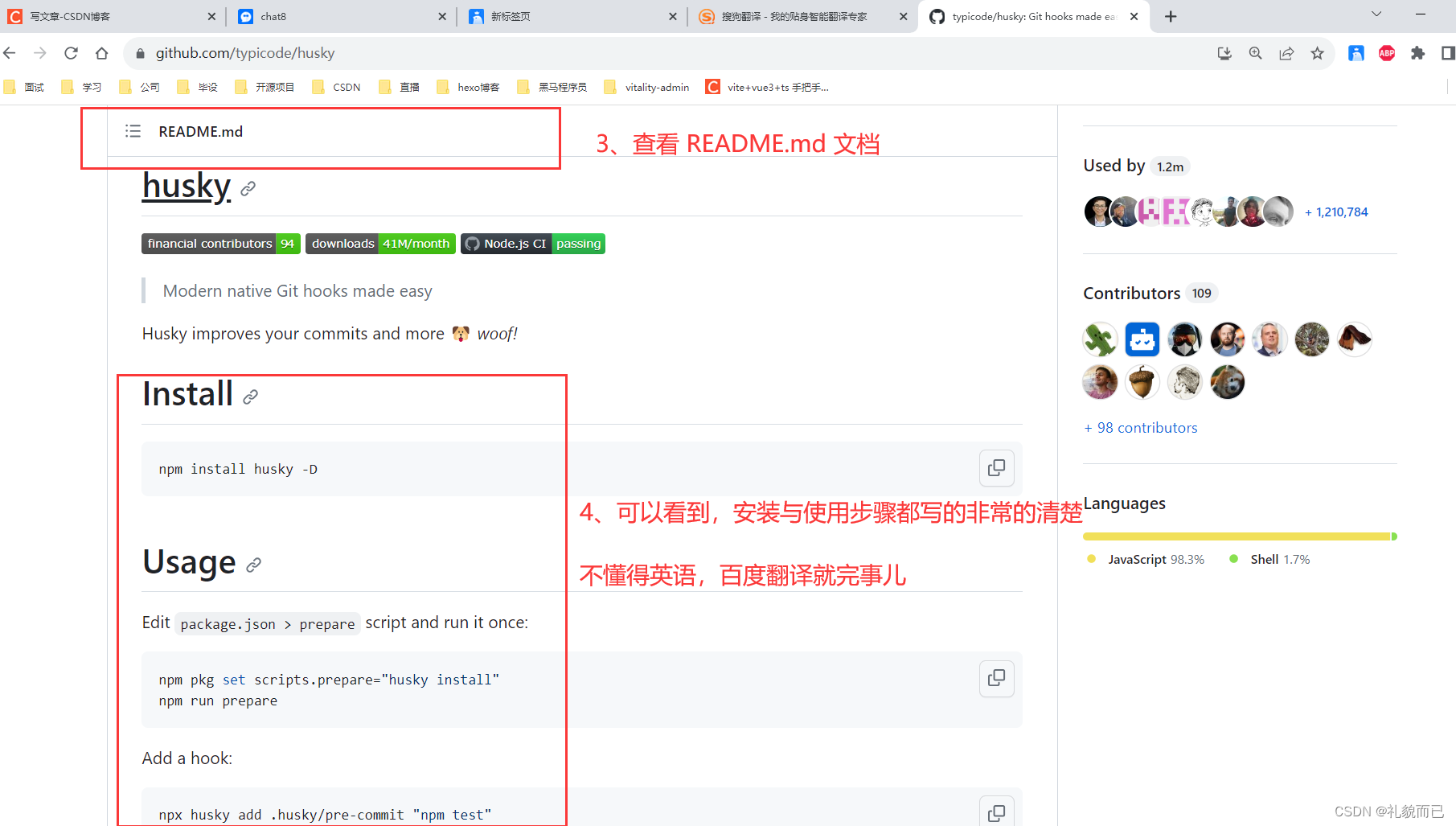
React18入门(第二篇)——React18+Ts项目配置husky、eslint、pretttier、commitLint
前言 我的项目版本如下: React: V18.2.0Node.js: V16.14.0TypeScript:最新版工具: VsCode 本文将采用图文详解的方式,手把手带你快速完成在React项目中配置husky、prettier、commitLint,实现编码规范的统…...
【VINS】苹果手机采集单目相机+IMU数据离线运行VINS-Mono
0.准备工作 开个新坑,之前用Android手机做过离线采集数据的实验,这次用IPhone来测试! 1.虚拟机配置Mac OS 下载一个Mac OS 的ios镜像,打开虚拟机按照跟Ubuntu差不多的方式安装,但是发现没有Mac OS的入口。 因为VMwa…...
数据结构 2.1 单链表
1.单链表 线性表:1.有限的序列 2.序列中的每一个元素都有唯一的前驱和后继,除了开头和结尾的两个节点。 顺序表:分配一块连续的内存去存放这些元素,eg、数组 链表:内存是不连续的,元素会各自被分配一块内…...
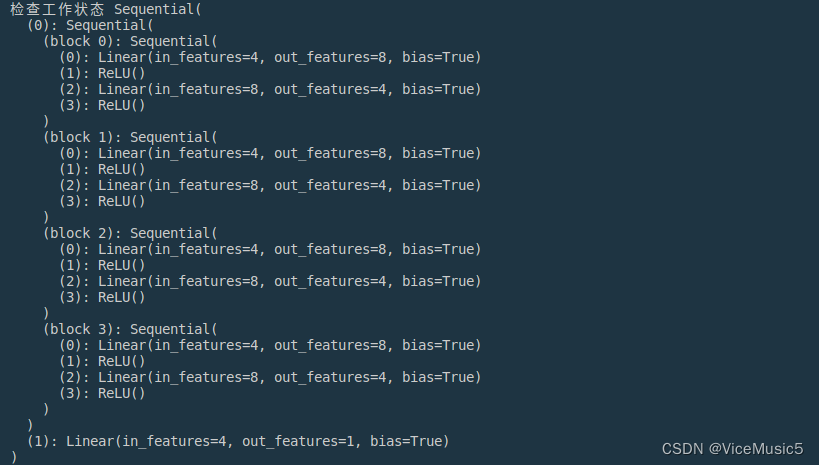
[Machine Learning]pytorch手搓一个神经网络模型
因为之前虽然写过一点点关于pytorch的东西,但是用的还是他太少了。 这次从头开始,尝试着搓出一个神经网络模型 (因为没有什么训练数据,所以最后的训练部分使用可能不太好跑起来的代码作为演示,如果有需要自己连上数据…...
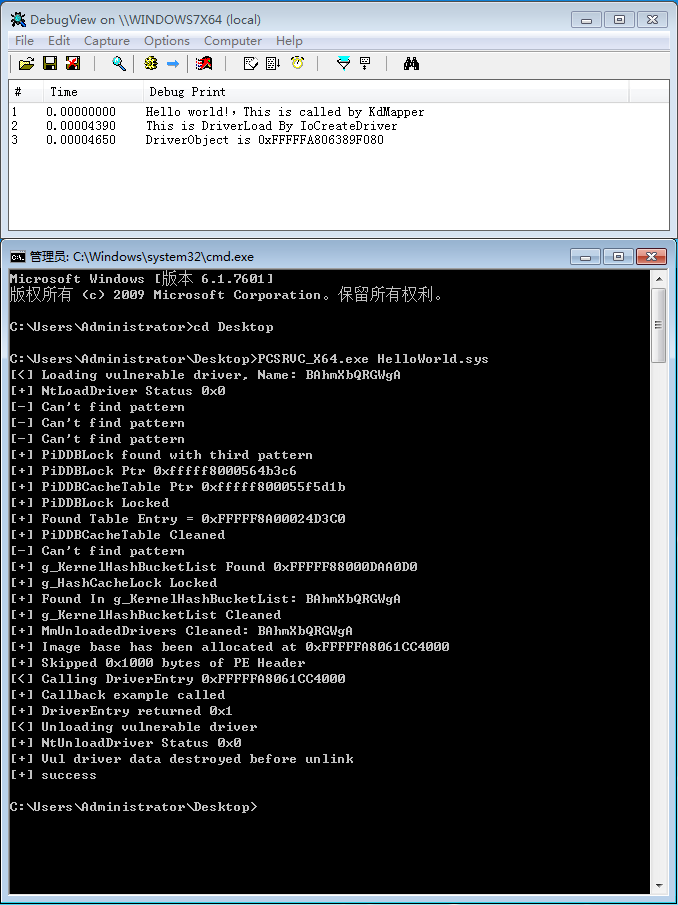
KdMapper扩展实现之Dell(pcdsrvc_x64.pkms)
1.背景 KdMapper是一个利用intel的驱动漏洞可以无痕的加载未经签名的驱动,本文是利用其它漏洞(参考《【转载】利用签名驱动漏洞加载未签名驱动》)做相应的修改以实现类似功能。需要大家对KdMapper的代码有一定了解。 2.驱动信息 驱动名称pcds…...

python和go相互调用的两种方法
前言 Python 和 Go 语言是两种不同的编程语言,它们分别有自己的优势和适用场景。在一些项目中,由于团队内已有的技术栈或者某一部分业务的需求,可能需要 Python 和 Go 相互调用,以此来提升效率和性能。 性能优势 Go 通常比 Python 更高效&…...

c# 分部视图笔记
Html.Partial("**", 1) public ActionResult **(int page) { ViewBag.page page; return PartialView("**"); }...

Vue3最佳实践 第七章 TypeScript 中
Vue组件中TypeScript 在Vue组件中,我们可以使用TypeScript进行各种类型的设置,包括props、Reactive和ref等。下面,让我们详细地探讨一下这些设置。 设置描述设置props在Vue中,props本身就具有类型设定的功能。但如果你希望使用Ty…...
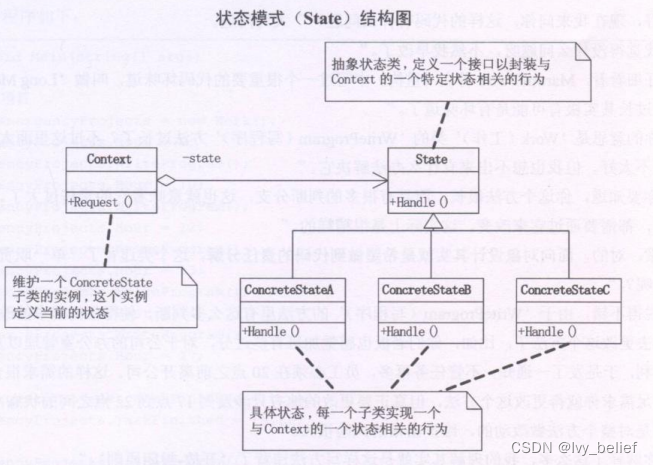
(三)行为模式:8、状态模式(State Pattern)(C++示例)
目录 1、状态模式(State Pattern)含义 2、状态模式的UML图学习 3、状态模式的应用场景 4、状态模式的优缺点 (1)优点 (2)缺点 5、C实现状态模式的实例 1、状态模式(State Pattern&#x…...
)
nginx的配置文件概述及简单demo(二)
默认配置文件 当安装完nginx后,它的目录下通常有默认的配置文件 #user nobody; worker_processes 1;#error_log logs/error.log; #error_log logs/error.log notice; #error_log logs/error.log info;#pid logs/nginx.pid;events {worker_connection…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...