面试 | 移位妙解递归乘法【细节决定成败】

不用[ * ]如何使两数相乘❓
- 一、题目明细
- 二、思路罗列 & 代码解析
- 1、野蛮A * B【不符合题意】
- 2、sizeof【可借鉴】
- 解析
- 3、简易递归【推荐】
- ① 解析(递归展开图)
- ② 时间复杂度分析
- 4、移位<<运算【有挑战性💪】
- ① 思路顺理
- ② 算法图解
- ③ 代码分析
- ④ 调试分析
- 📺视频解说
- 三、总结与提炼
一、题目明细
原题传送门

- 可能有读者会说为什么那么简单的题目也要写个题解?
- 答:【细节决定成败,不可忽视细枝末节】,对算法题的思考尽量要做到多维度考虑、多思考,继而找出最优解👑
二、思路罗列 & 代码解析
下面会列出我所AC的所有解,有些可能不符合题意
1、野蛮A * B【不符合题意】
本以为不让使用【*】运算符,但是试了一下,竟然也可以过😮
int multiply(int A, int B){return A * B;
}

2、sizeof【可借鉴】
这个方法我觉得还是比较巧妙,如果题目没有指定说要使用递归来进行求解,可以考虑
int multiply(int A, int B){char a[A][B];return sizeof(a);
}

解析
- 有很多学习完C语言的同学在使用
sizeof()的时候都会觉得它是一个函数,但真的是吗?其实可以去cpluplus中看看。就可以观测到无论是搜索多久都不会有结果

- 其实对于
sizeof()来说是一个操作符,而且是一个单目操作符,如果不清楚的可以看看我的操作符汇总大全。用来计算某一个数据类型的变量所占的字节大小。不要和Pascal中的sizeof()混淆了,在这门语言中是作为【函数】来看待的
在 Pascal 语言中,sizeof() 是一种内存容量度量函数,功能是返回一个变量或者类型的大小(以字节为单位);在 C语言中,sizeof() 是一个判断数据类型或者表达式长度的运算符《来源于百度百科》
- 所以在这道题中,其实我们利用两数相乘的这个逻辑,去定义一个字符型的二维数组,然后将这个数组当做是长方体,那对于长方体的面积来说就是
长 * 宽,那对于二维数组这个矩阵来说其实就是去计算它在内存中所占地字节数是多少,这样就可以很轻易地想到使用sizeof()去进行求解 - 这里要注意的是需定义为【字符数组】,因为
char类型的变量在内存中只占一个字节,若是定义为整型数组,算出来就是结果的4倍了!

3、简易递归【推荐】
这才是最符合题意的做法,使用递归去进行求解
class Solution {
public:int Mul(int big, int small){if(small == 0) return 0; //与0相乘一定为0if(small == 1) return big; //与1相乘一定为自身return big + Mul(big, small - 1); //small个big相加,small递减}int multiply(int A, int B) {//首先区分两者中的大的那个和小的那个int big = A > B ? A : B;int small = A < B ? A : B;return Mul(big, small);}
};

① 解析(递归展开图)
递归对有些同学来说可能不好理解,因此讲说一下代码逻辑
- 首先题目说到,两个数相乘不可以使用【*】号,那其实我们其看一下两个数相乘的原理也就是从加法转化过来的,
例1:3 * 4 == 4 + 4 + 4 | 例2:2 * 5 == 5 + 5 - 选取到小的那个数作为相加的次数
- 选取大的那个数作为相加的数字
- 在递归的函数中,若是发现
small == 0,那直接return 0即可,因为任何数和0相乘都是0 - 若是发现
small == 1,那就直接返回big,因为任何数和1相乘都是1 - 若是都不满足,则进行递归调用,注意要保留当前层的big,然后再产生递归让
small - 1即可
若是感觉有点抽象的话,就通过递归展开图来看看吧

② 时间复杂度分析
- 对于上面这种方法的时间复杂度为
O(N)。准确点来说是O(small),相当于一个线性阶。如果对时间复杂度如何计算不是很懂,可以看看我的这篇文章——> 时间与空间复杂度就看这篇了 - 那有没有更优的方法呢?就来看看下面这种吧
4、移位<<运算【有挑战性💪】
若是你搞懂了上面这种方法,那便来看看这种
移位<<这种方法吧,会让你更上一层楼
int Mul(int big, int small)
{if(small == 0) return 0;if(small == 1) return big;int half_small = small >> 1; //右移运算符,每次使small缩小一半//递归算出每一半的乘积int half_Sum = Mul(big, half_small); //判断每一层的递归中的small为偶数还是奇数if(small % 2 == 0){return half_Sum + half_Sum; //若为偶数直接是double倍}else{return half_Sum + half_Sum + big; //若为奇数则还需加上一个big}
}int multiply(int A, int B){//1.划分二者的大小int big = A > B ? A : B;int small = A < B ? A :B;int ret = Mul(big, small);return ret;
}

① 思路顺理
- 首先对于主接口函数还是一样,区分两者中谁大谁小,然后传入递归函数中
- 在递归函数中,我的思路是这样的,既然在上一题中想到了
线性阶,那便想要优化为对数阶,那对于对数阶而言一定存在一个二分的关系,然后就可以想到一半的关系 - 所以对于small个big相乘,其实并不需要加small次,加
small/2次即可,对于small/2次,其实也只需要加small/2次即可,那么这就相当于是一个递归的问题,要求出8个10的和,先求出4个10的和;要求出4个10的和,先求出2个10的和,要求出2个10的和,就先求出1个10,最后再进行层层回调,便可以算出small个big的和为多少了 - 不过这个small的情况还是判断其为奇数还是偶数:对于偶数来说就是一个二分,但是对于奇数来说就不一样了,因为÷2之后相当于是一个整除,
所以会漏掉一次的big相加,要在求当前和的最后加上一个big - 对于上述这种算法的时间复杂度很明显可以看出来是O(log2small)
② 算法图解
经过思路的讲解与分析,可能你还有些云里雾里😵那就通过算法分解图来看看吧
- small为偶数的情况

- small为奇数的情况

③ 代码分析
通过算法图的展示之后,相信你一定很清楚该如何去解决这个问题了,我们再来回顾一下代码
- 若是small进来直接为0,那么直接
return 0便可
if(small == 0) return 0;
- 这句便是算出当前层small的一半为多少,使用的便是移位运算符,
右移是缩小1/2
int half_small = small >> 1; //右移运算符,每次使small缩小一半
- 求出当前层small的一半之后,就继续进行递归,
//递归算出每一半的乘积
int half_Sum = Mul(big, half_small);
- 若是当递归调用的时候
small == 1了,便return big进行回调
if(small == 1) return big;
- 在回调之后,便会进行当前层一半总数的计算,这里就是我说的要对small进行奇偶数分类的情况
//判断每一层的递归中的small为偶数还是奇数
if(small % 2 == 0){return half_Sum + half_Sum; //若为偶数直接是double倍
}else{return half_Sum + half_Sum + big; //若为奇数则还需加上一个big
}
④ 调试分析
通过调试再来看看程序到底是如何运行的
- 以
big = 6, small = 4为例,进到递归函数中

- 通过右移运算符
>>便算出small的一半

- 继续递归,直到
small == 1为止

- 此时small便为1,执行
return big

- 递归回来之后便计算当前层的总和,因为
small == 2为偶数所以无需再加上big

- 此时继续回调,算出
small == 4这一层的总和

- 最后便通过递归计算出了【4 * 6】的和为24

为了更好地对照算法图,也来测试一下奇数的情况
- 这次的对比是运算是
big = 8, small = 6

- 可以看到,出现了
small为奇数的情况

- 继续递归,直到
small == 1为止

- 然后开始计算每一层的总和,注意:回到
small == 3的递归层时,要进入第二个if分支

- 此时就需要加上整除之后遗漏的那个big了

- 回到
small == 6的递归层时继续计算当前层的总和

- 最后就算出了
6 * 8 = 48的结果

📺视频解说
本文的题解都是通过看下面这位UP主写出来的,可以看看他的讲解——> 主页
leetcode 面试题 08.05. 递归乘法
三、总结与提炼
最后来总结一下本文所学习的内容📖
- 【递归乘法】这道题是LeetCode上的一道面试题,虽然题目看起来比较简单,但是递归对很多同学来说还是比较困难,所以我在这里做一个细致的讲解
- 主要是详细解说了有关递归的两种解法,对于简易递归来说就是本题的答案,但是我们要像在面试中胜出,就必须要想到更好、更优的解法;对于第二种
sizeof的解法,可供读者参考,也是比较巧妙的方法,不过要清楚sizeof是一个操作符,而不是一个函数
学会不断思考,不断突破自己,才是最大的进步

相关文章:

面试 | 移位妙解递归乘法【细节决定成败】
不用[ * ]如何使两数相乘❓一、题目明细二、思路罗列 & 代码解析1、野蛮A * B【不符合题意】2、sizeof【可借鉴】解析3、简易递归【推荐】① 解析(递归展开图)② 时间复杂度分析4、移位<<运算【有挑战性💪】① 思路顺理② 算法图解…...
项目缓存问题处理
1、public/index.html文件头部配置 <meta http-equiv"pragram" content"no-cache"> <meta http-equiv"cache-control" content"no-cache,no-store,must-revalidate"> <meta http-equiv"expires" content&…...

DS期末复习卷(八)
一、选择题(30分) 1.字符串的长度是指( C )。 (A) 串中不同字符的个数 (B) 串中不同字母的个数 (C ) 串中所含字符的个数 (D) 串中不同数字的个数 2.建立一个长度为n的有序单链表的时间复杂度为( C ) (A) O(n) (B) O(1) © …...

第50讲:SQL优化之LIMIT分页查询的优化
文章目录 1.LIMIT分页查询的优化概念2.LIMIT分页查询优化前后的效果2.1.LIMIT分页查询优化前2.2.LIMIT分页查询优化后1.LIMIT分页查询的优化概念 当表中数据量小时,分页查询基本上没有什么压力,查询速度也会很快,但是一般当表的数据量很庞大时,上千万条数据,此时分页查询…...

做独立开发者,能在AppStore赚到多少钱?
成为一名独立开发者,不用朝九晚五的上班,开发自己感兴趣的产品,在AppStore里赚美金,这可能是很多程序员的梦想,今天就来盘一盘,这个梦想实现的概率有多少。 先来了解一些数据: 2022年5月26日&am…...
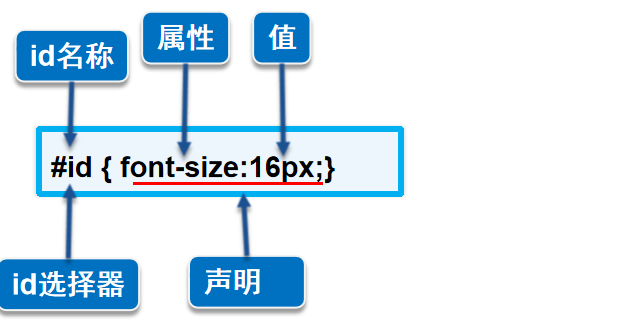
CSS 基础【快速掌握知识点】
目录 一、什么是CSS 二、CSS发展史 三、CSS基本语法结构 1、语法 2、例如 四、style标签 五、HTML中引入CSS样式 1、行内样式 2、内部样式表 3、外部样式表 六、CSS基本选择器 1、标签选择器 2、类选择器 3、ID选择器 4、总结 5、基本选择器的优先级 七、CSS的…...

Linux 驱动基础
注册驱动模块时给模块传递参数 在一些情况下,我们要动态的改变驱动中某个变量的值,那么就可以在注册时给驱动模块传递参数。 给驱动模块中传递参数,需要定义好接受参数值的全局变量,并调用module_param 来引用它,具体…...
)
linux 共享内存操作(shm_open、mmap、编译链接库:-lz -lrt -lm -lc都是什么库)
文章目录linux 共享内存操作(shm_open)一、背景二、函数使用说明shm_openftruncate(改变文件大小)mmap共享内存三、示例代码创建内存共享文件并写入数据打开内存共享文件读数据四、问题总结shm_write.c:(.text0x18): undefined re…...

做出改变:农业科技和区块链在为地球的未来而战中的力量
到2050年,全球有100亿人需要养活,全世界都在关注区块链和农业信息化,以推动发展中国家的技术革新。 自成立以来,区块链技术已经找到了多样化和有价值的应用,以帮助提高效率和激励社区在不同领域和行业的参与。 农业是…...

树莓派介绍
文章目录一.树莓派介绍二.树莓派分类一.树莓派介绍 树莓派,(英语:Raspberry Pi,简写为RPi,别名为RasPi / RPI)是为学习计算机编程教育而设计,只有信用卡大小的微型电脑,其系统基于L…...
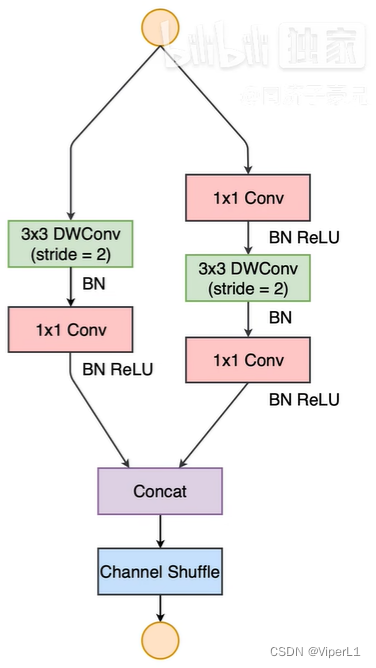
[神经网络]基干网络之VGG、ShuffleNet
一、VGG VGG是传统神经网络堆叠能达到的极限深度。 VGG分为VGG16和VGG19,其均有以下特点: ①按2x2的Pooling层,网络可以分成若干段 ②每段之内由若干same卷积操作构成,段内Feature Map数量固定不变; ③Feature Map按2的…...

Java 日期时间与正则表达式,超详细整理,适合新手入门
目录 1、java.time.LocalDate类表示日期; 2、java.time.LocalTime类表示时间; 3、java.time.LocalDateTime类表示日期和时间; 4、java.time.format.DateTimeFormatter类用于格式化日期和时间; 5、创建正则表达式对象 6、匹配…...

用Netty实现物联网04:自定义通信协议
上一讲咱们澄清了Netty的一些基本概念,然后也写了一个服务端与客户端通信的简单应答程序。从这一讲开始,就来一步步搭建一个Netty物联网应用。 大多数硬件电子产品,都自带了嵌入式软件,或者说固件。这些嵌入式软件/固件基本上都是用C/C++编写的。由于这些小微电子设备资源极…...
「smardaten」上架钉钉应用中心!让进步再一次发生
使用钉钉的团队小伙伴们,smardaten给您送来福利啦~为了给更多团队提供更优质的应用开发体验,方便用户在线、快速使用无代码,数睿数据近期在【钉钉应用中心】发布smardaten在线版本。继与华为云、亚马逊云建立战略合作之后,smardat…...
3、Maven安装
前言:工具下载地址阿里云盘:Maven:https://www.aliyundrive.com/s/SgHKjQ5doSp提取码: ml40一、什么是maven?Apache Maven是个项目管理和自动构建工具,基于项目对象模型(POM)的概念。作用:完成…...

tkinter
# 隐藏控件 tl.pack_forget() tb.pack_forget() # 显示控件 tl.pack() tb.pack() 如果您使用 grid 布局管理器,则可以使用 grid_remove() 方法将控件隐藏,使用 grid() 方法将控件显示。例如: # 隐藏控件 tl.grid_remove() tb.grid_remove() #…...
:HTTP状态码)
Servlet笔记(6):HTTP状态码
1、状态码 代码消息描述100 Continue只有请求的一部分已经被服务器接收,但只要它没有被拒绝,客户端应继续该请求。101 Switching Protocols服务器切换协议。200 OK请求成功。201 Created该请求是完整的,并创建一个新的资源。202 Accepted该请…...
RocketMQ 延迟队列
什么是延迟队列指消息发送到某个队列后,在指定多长时间之后才能被消费。应用场景RocketMQ 延迟队列定时消息(延迟队列)是指消息发送到broker后,不会立即被消费,等待特定时间投递给真正的topic。broker有配置项messageD…...

【精准计时】北斗GPS卫星时钟同步改变精准计时年代
【精准计时】北斗GPS卫星时钟同步改变精准计时年代 【精准计时】北斗GPS卫星时钟同步改变精准计时年代 北斗GPS成精确计时先锋 北斗GPS精确时间自动校准技术,是一种简便的获取北斗GPS精确时间信息的专利技术,具有灵敏度高、不受时间及地域限制等特点…...

【C#基础】C# 面向对象编程
序号系列文章5【C#基础】C# 运算符总结6【C#基础】C# 常用语句讲解7【C#基础】C# 常用数据结构文章目录前言面向对象的 C#1,类的概念2,类的定义3,类成员4,对象5,继承6,多态性结语前言 😊大家好&…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
