数据结构与算法入门
目录
- 数据结构概述
- 逻辑结构
- 存储结构
- 算法概述
- 如何理解“大O记法”
- 时间复杂度
- 空间复杂度
数据结构概述
- 数据结构可以简单的理解为数据与数据之间所存在的一些关系,数据的结构分为数据的存储结构和数据的逻辑结构。
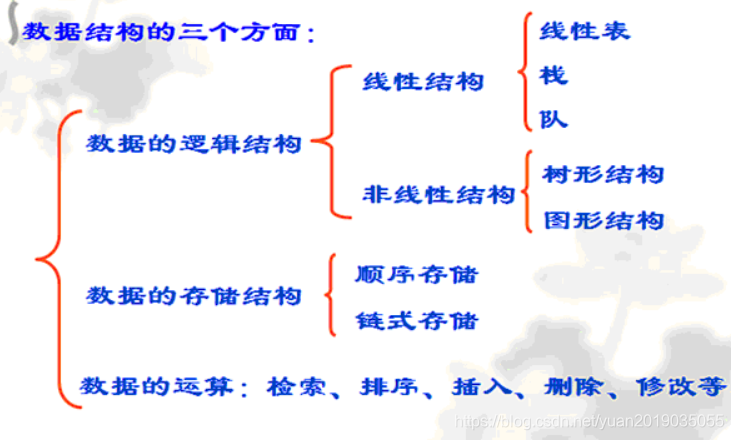
逻辑结构
- 集合结构:数据元素同属于一个集合,他们之间是并列关系,无其他的关系;可以理解为中学时期学习的集合,在一个范围之内,有很多的元素,元素间没有什么关系
- 线性结构:元素之间存在着一对一的关系;可以理解为每个学生对应着一个学号,学号与姓名就是线性结构
- 树形结构:元素之间存在着一对多的关系,可以简单理解为家庭族谱一样,一代接一代
- 图形结构:元素之间存在多对多的关系,每一个元素可能对应着多个元素,或被多个元素对应,网状图
存储结构
- 顺序存储结构:就是将数据进行连续的存储,我们可以将它比喻成学校食堂打饭排队一样,一个接着一个;
- 链式存储结构:不是按照顺序存储的,后一个进来的数只需要将他的地址告诉前一个节点,前一个节点中就存放了它后面那个数的地址,所以最后一个数的存储地址就是为null;可以将这种结构比喻成商场吃饭叫号,上面的号码比喻成是地址,你可以之后后面的地址是什么,上面的其他内容就是该节点的内容;
- 区别:
- 顺序存储的特点是查询快,插入或者删除慢
- 链式存储的特点是查询慢,插入或者删除快
算法概述
- 同一问题不同解决方法
- 通过时间和空间复杂度判断算法的优劣
- 算法没有最好的,只有最合适的,学习算法是为了积累学习思路,掌握学习思路,并不是为了解决某问题去记住某种算法;对于时间复杂度与空间复杂度,现在大多数开发情况下,我们都在使用以空间换时间,耗费更多的内存,来保证拥有更快的速度。
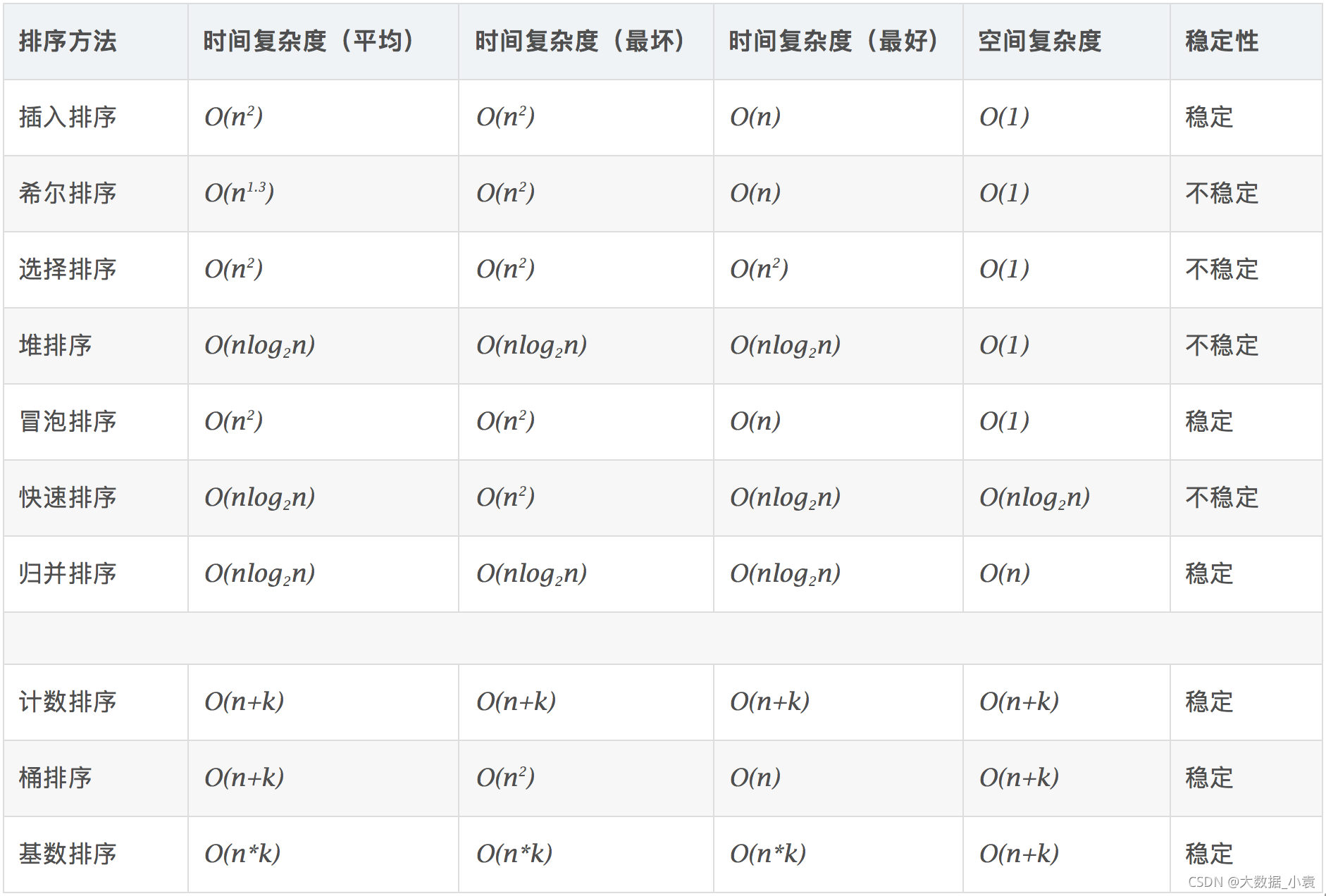
- 各排序算法复杂度及稳定性:
如何理解“大O记法”
对于算法进行特别具体的细致分析虽然很好,但在实践中的实际价值有限。对于算法的时间性质和空间性质,最重要的是其数量级和趋势,这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。例如,可以认为 3n^2 和 100n^2 属于同一个量级,如果两个算法处理同样规模实例的代价分别为这两个函数,就认为它们的效率“差不多”,都为n^2级。
时间复杂度
一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。算法中的语句执行次数称为语句频度或时间频度,记为T(n)。n 称为问题的规模,当 n 不断变化时,时间频度T(n)也会不断变化。但有时我们想知道它变化时呈现什么规律。为此,我们引入时间复杂度概念。
一般情况下,算法中基本操作重复执行的次数是问题规模 n 的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当 n 趋近于无究大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n))为算法的渐进时间复杂度,简称时间复杂度。
有时候,算法中基本操作重复执行的次数还随问题的输入数据集不同而不同,如在冒泡排序中,输入数据有序而无序,结果是不一样的。此时,我们计算平均值。
时间复杂度基本计算规则:
- 基本操作,即只有常数项,认为其时间复杂度为O(1)
- 顺序结构,时间复杂度按加法进行计算
- 循环结构,时间复杂度按乘法进行计算
- 分支结构,时间复杂度取最大值
- 判断一个算法的效率时,往往只需要关注操作数量的最高次项,其它次要项和常数项可以忽略
- 在没有特殊说明时,我们所分析的算法的时间复杂度都是指最坏时间复杂度
常用时间复杂度:
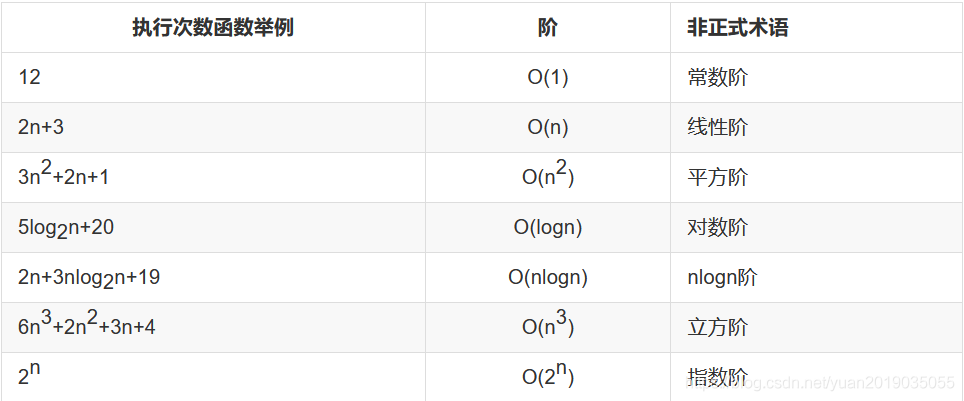
注意:经常将log2n(以2为底的对数)简写成logn
常见时间复杂度之间的关系:
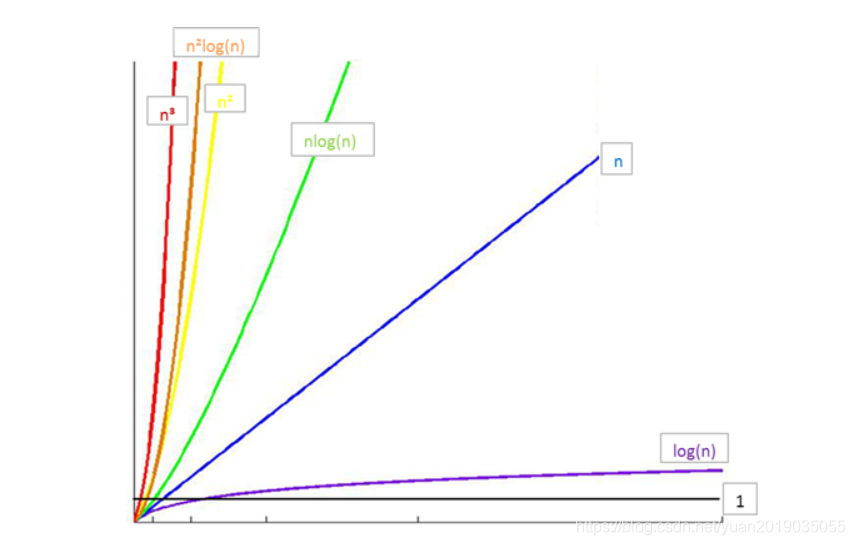
- 所以时间消耗由小到大为:
O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(2^n) < O(n!) < O(n^n)
案例1:
count = 0; (1)for(i = 0;i <= n;i++) (2)for(j = 0;j <= n;j++) (3)count++; (4)
- 语句(1)执行1次
- 语句(2)执行n次
- 语句(3)执行n^2次
- 语句(4)执行n^2次
- 时间复杂度为:
T(n) = 1+n+n^2+n^2 = O(n^2)
案例2:
a = 1; (1)
b = 2; (2)
for(int i = 1;i <= n;i++) { (3)int s = a + b; (4)b = a; (5)a = s; (6)
}
- 语句(1)、(2)执行1次
- 语句(3)执行n次
- 语句(4)、(5)、(6)执行n次
- 时间复杂度为:
T(n) = 1+1+4n = o(n)
案例3:
i = 1; (1)
while(i<n) {i = i*2; (2)
}
- 语句(1)的频度是1
- 设语句(2)的频度是
f(n),则2f(n)<=n;f(n)<=log2n,取最大值f(n) = log2n - 时间复杂度为:
T(n) = O(log2n)
空间复杂度
-
算法的空间复杂度计算公式:
S(n) = 0( f(n) ),其中 n 为输入规模,f(n)为语句关于 n 所占存储空间的函数 -
一个算法在计算机存储器上所占用的存储空间,包括三个方面
- 存储算法本身所占用的存储空间
- 算法的输入输出数据所占用的存储空间
- 算法在运行过程中临时占用的存储空间
案例:指定的数组进行反转,并返回反转的内容
解法一:
public static int[] reverse1(int[] arr) {int n = arr.length; //申请4个字节int temp; //申请4个字节for (int start = 0, end = n - 1; start <= end; start++, end--) {temp = arr[start];arr[start] = arr[end];arr[end] = temp;}return arr;
}
- 空间复杂度为:
S(n) = 4+4 = O(8) = O(1)
解法二:
public static int[] reverse2(int[] arr) {int n = arr.length; //申请4个字节int[] temp = new int[n]; //申请n*4个字节+数组自身头信息开销24个字节for (int i = n - 1; i >= 0; i--) {temp[n - 1 - i] = arr[i];}return temp;
}
- 空间复杂度为:
S(n) = 4+4n+24 = O(n+28) = O(n)
根据大O推导法则,算法一的空间复杂度为0(1),算法二的空间复杂度为0(n),所以从空间占用的角度讲,算法一要优于算法二。
由于java中有内存垃圾回收机制,并且jvm对程序的内存占用也有优化(例如即时编译) , 我们无法精确的评估一个java程序的内存占用情况,但是了解了java的基本内存占用,使我们可以对java程序的内存占用情况进行估算。
由于现在的计算机设备内存一般都比较大,基本上个人计算机都是4G起步,大的可以达到32G ,所以内存占用一般情况下并不是我们算法的瓶颈,普通情况下直接说复杂度,默认为算法的时间复杂度。
但是,如果你做的程序是嵌入式开发,尤其是一些传感器设备上的内置程序,由于这些设备的内存很小, 一般为几kb,这个时候对算法的空间复杂度就有要求了,但是一般做java开发的,基本上都是服务器开发, 一般不存在这样的问题。
相关文章:

数据结构与算法入门
目录数据结构概述逻辑结构存储结构算法概述如何理解“大O记法”时间复杂度空间复杂度数据结构概述 数据结构可以简单的理解为数据与数据之间所存在的一些关系,数据的结构分为数据的存储结构和数据的逻辑结构。 逻辑结构 集合结构:数据元素同属于一个集…...

【OpenAI】基于 Gym-CarRacing 的自动驾驶练习项目 | 路径训练功能的实现 | GYM-Box2D CarRacing
限时开放,猛戳订阅! 👉 《一起玩蛇》🐍 💭 写在前面: 本篇是关于多伦多大学自动驾驶专业项目的博客。GYM-Box2D CarRacing 是一种在 OpenAI Gym 平台上开发和比较强化学习算法的模拟环境。它是流行的 Box2…...

亚马逊、沃尔玛测评自养号测评、退款、撸卡撸货怎么做?
大家好,有很多的测评工作室做亚马逊测评、沃尔玛测评自养号大额退款,撸卡撸货的找到我,问我有什么方式可以解决成本,效率,纯净度,便捷性等问题,测评养号系统从最早的模拟器,虚拟机到…...
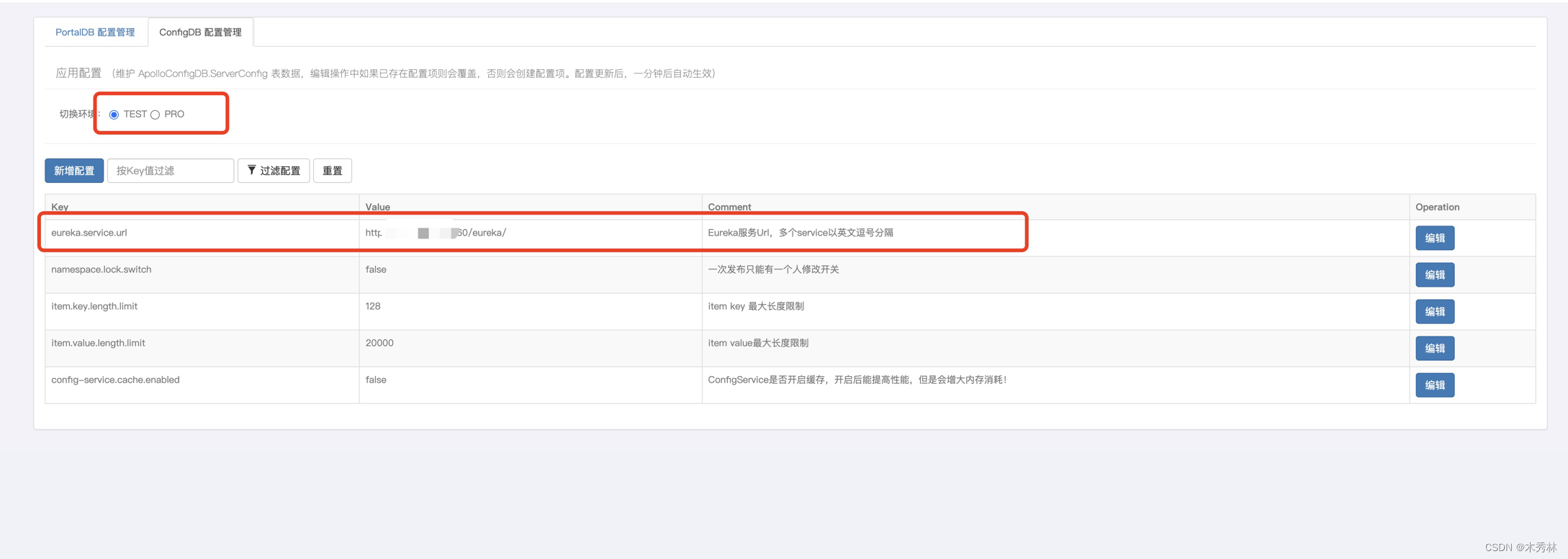
Apollo 2.1.0最新版docker 部署多环境 与java spring boot 接入demo (附带一键部署脚本)
最新Apollo 版本发布2.1.0 https://www.apolloconfig.com/#/zh/design/apollo-design 环境说明 ecs 主机一台数据库mysql 8.0docker 环境 apollo 是内网可信应用,最好是部署在内网里面,外网不可使用,避免配置信息泄漏,这里为了方…...
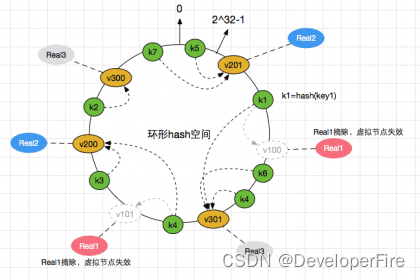
分布式算法 - 一致性Hash算法
一致性Hash算法是个经典算法,Hash环的引入是为解决单调性(Monotonicity) 的问题;虚拟节点的引入是为了解决 平衡性(Balance) 问题。一致性Hash算法引入在分布式集群中,对机器的添加删除,或者机器故障后自动脱离集群这些操作是分布…...
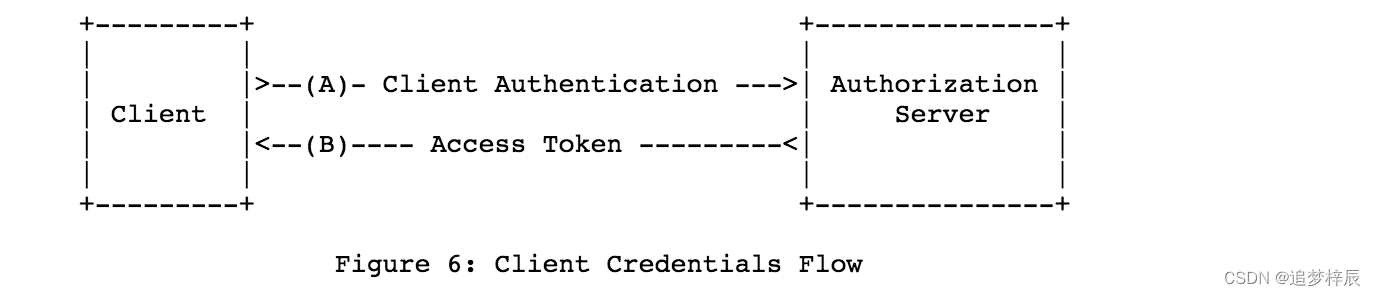
OAuth2.0入门
什么是OAuth2.0 OAuth(Open Authorization)是一个关于授权(authorization)的开放网络标准,允许用户授权第三方应用访问他们存储在另外的服务提供者上的信息,而不需要将用户名和密码提供给第三方移动应用或…...

【HTTP——了解HTTP协议及状态码】
一, 什么是通信通信,就是信息的传递和交换。通信三要素:通信的主体,通信的内容,通信的方式现实生活中的通信:我打电话叫小明来我家吃饭【其中通信的主体是,我,小明。通信内容是&…...

骨传导耳机靠谱吗,骨传导耳机的原理是什么
很多人刚开始接触骨传导耳机时都会具有一个疑问,骨传导耳机是不是真的靠谱,是不是真的不伤害听力?骨传导耳机传输声音的原理是什么? 下面就给大家讲解一下骨传导耳机传输声音的原理以及骨传导耳机对听力到底有没有伤害。 骨传导…...
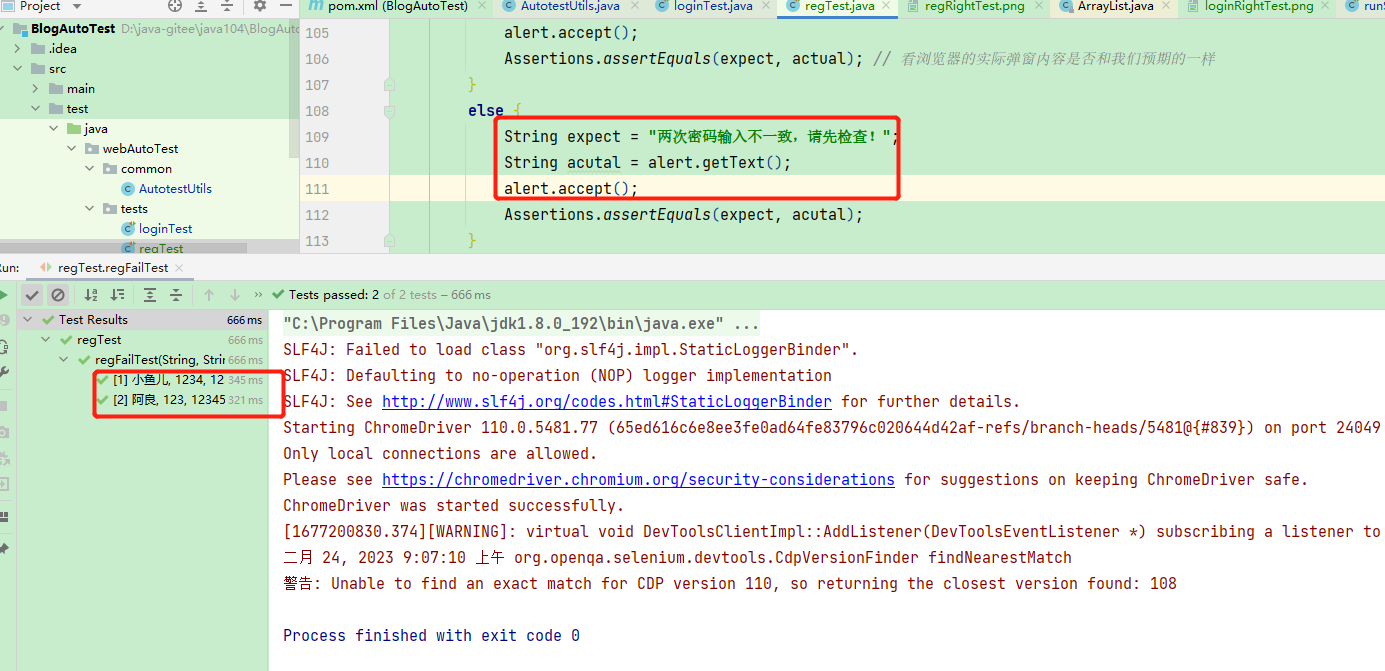
对个人博客系统进行web自动化测试(包含测试代码和测试的详细过程)
目录 一、总述 二、登录页面测试 一些准备工作 验证页面显示是否正确 验证正常登录的情况 该过程中出现的问题 验证登录失败的情况 关于登录界面的总代码 测试视频 三、注册界面的自动化测试 测试代码 过程中出现的bug 测试视频 四、博客列表页测试(…...

[ 2204听力 ] 五
[ 第五次课 对话1 ] Narrator Listen to a conversation between a student and her Ecology professor (woman) Hi, professor, did you want to talk about my paper? I didn’t get a grade. (man) Ah, yes, I think you might have done the wrong assignment. assign…...
嵌入式常问问题和知识
12、并发和并行的区别? 最本质的区别就是:并发是轮流处理多个任务,并行是同时处理多个任务。 你吃饭吃到一半,电话来了,你一直到吃完了以后才去接,这就说明你不支持并发也不支持并行。 你吃饭吃到一半&…...

【数据结构】空间复杂度
🚀write in front🚀 📜所属专栏:初阶数据结构 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论,是对…...

湖南中创教育提醒校外培训留意这几点,避免维权
校外教育培训机构是市场经济发展的必然产物,有需求就有市场,这个无可厚非。而校外教育培训机构的火热,正是反映出人民群众对教育发展的需求在不断增强。 培训机构分类中有面对大学生参加公务员招考、教师考编等考证考试的培训机构࿱…...

docker 配置私有/本地镜像仓库
docker 配置私有/本地镜像仓库docker pull registry mkdir -p /usr/local/docker/registry-data docker tag registry 192.168.28.132:5000/registry docker run -di -p 5000:5000 --namelocal_registry --restartalways --privilegedtrue --log-drivernone -v /usr/local/d…...

每日学术速递2.23
Subjects: Robotics 1.On discrete symmetries of robotics systems: A group-theoretic and data-driven analysis 标题:关于机器人系统的离散对称性:群论和数据驱动分析 作者:Daniel Ordonez-Apraez, Mario Martin, Antonio Agudo, F…...

LeetCode 232. 用栈实现队列
LeetCode 232. 用栈实现队列 难度:easy\color{Green}{easy}easy 题目描述 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(pushpushpush、poppoppop、peekpeekpeek、emptyemptyempty): 实现 MyQueueM…...

AI算法创新赛-人车目标检测竞赛总结04
队伍:AI000038 小组成员:杨志强,林松 1. 算法介绍 1.1 相关工作 当前流行的目标检测算法主要分为三种,一阶段算法:SSD,FCOS,Scaled,YOLO系列等;二阶段算法:…...

【C语言进阶】动态内存管理详解与常见动态内存错误以及柔性数组使用与介绍
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C语言进阶 🎯长路漫漫浩浩,万事皆有期待 文章目录1.动态内存1.1 概述…...

【C++】string的模拟实现
文章目录1. string的模拟实现1.构造函数使用new开辟空间优化成全缺省的构造函数2. C_str3. operator[]4.拷贝构造浅拷贝深拷贝5. 赋值三种情况6. 迭代器7.比较(ASCII值)大小8. reserve(扩容)9. push_back(尾插字符)10. append(尾插字符串)11. (字符/字符串)12. insert在pos位置…...
前端借助Canvas实现压缩base64图片两种方法
一、具体代码 1、利用canvas压缩图片方法一 // 第一种压缩图片方法(图片base64,图片类型,压缩比例,回调函数)// 图片类型是指 image/png、image/jpeg、image/webp(仅Chrome支持)// 该方法对以上三种图片类型都适用 压缩结果的图片base64与原类型相同// …...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
