归并排序与非比较排序详解

W...Y的主页 😊
代码仓库分享 💕

🍔前言:
上篇博客我们讲解了非常重要的快速排序,相信大家已经学会了。最后我们再学习一种特殊的排序手法——归并排序。话不多说我们直接上菜。
目录
归并排序
基本思想
递归思路
算法思路
代码思路以及实现
非递归思路
算法思路编辑
代码思路以及实现
归并排序的特性总结
非比较排序
计数排序
算法思路以及代码实现
计数排序总结
八大排序总结
归并排序
基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
递归思路
算法思路
归并排序的思路就是先分再合。
1.我们将一个数组进行平分,然后继续递归进行更细小的划分秒,直到每个数组如同一个数组时,然后再进行返回。
2.返回时每个小数组中的数必须排列为有序的数。
3.然后合并每个小数组,然后继续进行排序直到数组有序即可。
我们可以展示一下归并排序的动图,让大家更好的理解:

代码思路以及实现
不难看出递归的过程非常像二叉树的后序遍历数组,如果左右区间都无序,我们进行向下递归,直到有序再返回合并。(只有一个数时,我们可以看作其有序)
所以我们的代码思路也与二叉树后序代码有点相似。
具体思路:
1.创建一个与原数组相同空间大小的数组用来拷贝已经排序好的子数组。
2.创建一个函数来进行递归调用,如果使用有malloc的函数,递归时会重复开辟空间导致空间浪费,函数的参数传入原数组,新建数组与排序的起始位置与终止位置。
3.进行数组的递归调用。
4.创建临时遍历begin1、end1、begin2、end2,控制子数组的区间,然后进行比较排序成为有序子数组。
5.将有序的数组先放入新数组中,然后拷贝到原数组中进行覆盖,变为有序数组即可。
代码实现:
void _MergeSort(int* a, int* tmp, int begin, int end)
{if (end <= begin)return;int mid = (end + begin) / 2;//[begin, min][min + 1, end]_MergeSort(a, tmp, begin, mid);_MergeSort(a, tmp, mid + 1, end);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int index = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, tmp, 0, n - 1);free(tmp);
}
易错点:
在拷贝时,我们不一定是从头进行拷贝,拷贝的都是与数组头的相对位置,所以在参数中我们要添加begin。
非递归思路
为什么要进行非递归,与快速排序的原因相同,就是因为递归占用的是栈空间,而栈空间的内存非常小,所以我们要进行非递归的算法学习。而非递归与斐波那契切数的思路相当,就是已知前两个然后去推后面的数,而归并的非递归也是如此,将思路进行正向整理,从最小的开始进行即可。
算法思路

我们先创建一个gap数进行子数组大小记录,gap为1则进行一一比较排序,gap = 2则进行两个两个比较以此类推。后面与递归思路基本相同。
代码思路以及实现
实现思路:
1.模拟递归最后一层进行比较排序。
2.每次gap *= 2.
3.当gap>=n时停止递归。
4.将有序数组进行拷贝
代码实现:
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int*) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int index = i;if (begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}printf("[%d][%d][%d][%d] ", begin1, end1, begin2, end2);while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}printf("\n");gap *= 2;}free(tmp);
} 注意:当我们进行排序时,我们就会进行分组。但是有些数组中的元素个数不一定够组成一组。当我们一个一个进行分组时,我们可以将所以元素分为一组,但是当个数为奇数时,我们进行归并后进行两个一组时,就会有一个剩余。四个进行分组时也会有其中一组或两组没有分满的情况,所以我们如果不进行控制,就会出现数组越界的情况,程序就会报错。
我们将每一次的递归区间进行打印即可看出区间越界的问题:
 但是我们进行修改后就不会出现越界情况:
但是我们进行修改后就不会出现越界情况:

其中越界的有end2、begin2、end1。begin1是不会越界的。那我们将其进行边界的修正,这样即不会影响正常的归并,也不会将出错的情况算入其中。
处理方法:
如果end2越界,则将其修改为n-1。
如果begin2和end1越界,则将其修正为不存在的区间,不存在则直接跳出了归并的过程。
共用三种出界情况.
但是如果begin2越界或end1越界程序直接break即可,其实直接写begin2就可以涵盖所有情况,所以我们可以将begin1>n省略。
归并排序的特性总结
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定
非比较排序
非比较排序的思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中
计数排序
计数排序是一种比较新奇的排序思路,它没有两两数之间的比较,而是统计每个数出现的次数,然后进行排序。
这种方法适合于数目比较集中的情况,且整型数据。
时间复杂度:O(N + range) 空间复杂度:O(range)
算法思路以及代码实现
思路:
1.先寻找数组中出现的最大数与最小数。
2.开辟最大数-最小数差值的数组空间大小
3.遍历数组,统计数组中每个数出现的次数放入开辟好的数组中去。
4.遍历新建数组中的内容,每个数出现几次,就在旧数组中打印几次,覆盖掉原数组的内容。
代码实现:
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (size_t i = 0; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);printf("range:%d\n", range);if (count == NULL){perror("malloc fail");return;}memset(count, 0, sizeof(int) * range);// 统计数据出现次数for (int i = 0; i < n; i++){count[a[i] - min]++;}// 排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}注意:我们统计的数组不一定从0开始,所以我们在统计出数组中的最小值时一定要在默认在每个下标后加最小值才可以得到原数组中的内容。
计数排序总结
计数排序的特性总结:
1. 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
2. 时间复杂度:O(MAX(N,范围))
3. 空间复杂度:O(范围)
八大排序总结
总结:几种常见易错且重要的排序在这里就讲述完了,我们要合理引用,发挥出排序的优点,舍弃其缺点。最后我将这些排序的复杂度以及稳定性进行了总结,我们可以适度观看。 
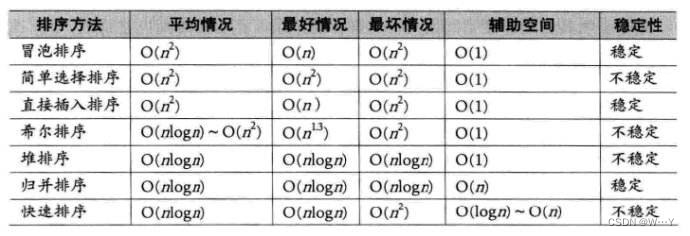
以上就是本次博客全部内容,感谢大家观看!!!
相关文章:

归并排序与非比较排序详解
W...Y的主页 😊 代码仓库分享 💕 🍔前言: 上篇博客我们讲解了非常重要的快速排序,相信大家已经学会了。最后我们再学习一种特殊的排序手法——归并排序。话不多说我们直接上菜。 目录 归并排序 基本思想 递归思路…...
第85步 时间序列建模实战:CNN回归建模
基于WIN10的64位系统演示 一、写在前面 这一期,我们介绍CNN回归。 同样,这里使用这个数据: 《PLoS One》2015年一篇题目为《Comparison of Two Hybrid Models for Forecasting the Incidence of Hemorrhagic Fever with Renal Syndrome i…...
【MATLAB源码-第36期】matlab基于BD,SVD,ZF,MMSE,MF,SLNR预编码的MIMO系统误码率分析。
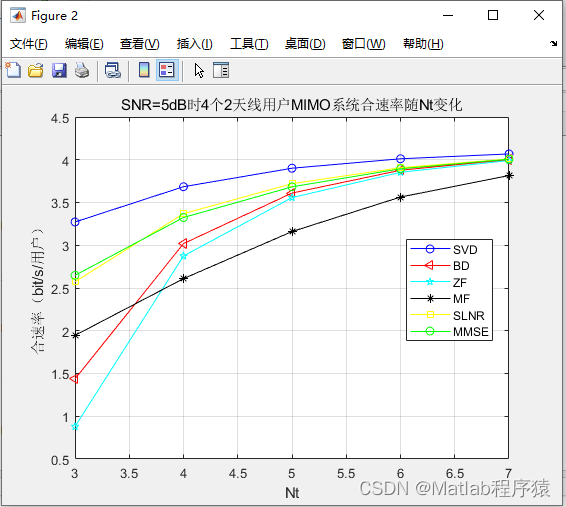
1、算法描述 1. MIMO (多输入多输出):这是一个无线通信系统中使用的技术,其中有多个发送和接收天线。通过同时发送和接收多个数据流,MIMO可以增加数据速率和系统容量,同时提高信号的可靠性。 2. BD (块对角化):这是一…...

Uniapp 新手专用 抖音登录 获取用户头像、名称、openid、unionid、anonymous_openid、session_key
TC-dylogin 一定请选择 源码授权版 教程 第一步 将代码拷贝至您所需要的页面 该代码位置:pages/index.vue 第二步 修改appid和secret 第三步 获取appid和secret 获取appid和secret链接 注意事项 为了安全,我将默认的自己的appid和secret在云函数中删…...

openssl引擎开发踩坑小记
前言 在开发openssl引擎过程中,引擎莫名其妙的加载不上,错误如下图: 大概意思就是加载引擎动态库时失败了。 在网上一顿搜索后,也没找到想要的答案。 原因 许多引擎都是基于第三方动态库开发的,引擎本身在开发时&a…...
ubuntu 设置x11vnc服务
Ubuntu 18.04 设置x11vnc服务 自带的vino-server也可以用但是不好用,在ubuntu论坛上看见推荐的x11vnc(ubuntu关于vnc的帮助页面),使用设置一下,结果发现有一些坑需要填,所以写下来方便下次使用 转载请说明…...

物理备份xtrabackup
物理备份: 直接复制数据库文件,适用于大型数据库环境,不受存储引擎的限制,但不能恢复到不同的MySQL版本。 1.完全备份-----完整备份: 每次都将所有数据(不管自第一次备份以来有没有修改过)&am…...
1.springcloudalibaba nacos2.2.3部署
前言 nacos是springcloudalibaba体系的注册中心,演示如何搭建最新稳定版本的linux搭建。 前置条件,安装好jdk1.8 一、二进制压缩包下载 1.1 下载压缩包 nacos下载 点击下载下载后得到二进制包如下 nacos-2.2.3.tar.gz二、安装步骤 2.1.解压二进制…...
Linux 查看是否安装memcached
telnet 127.0.0.1 11211这样的命令连接上memcache,然后直接输入stats就可以得到memcache服务器的版本 安装memcached : sudo apt-get install memcached...
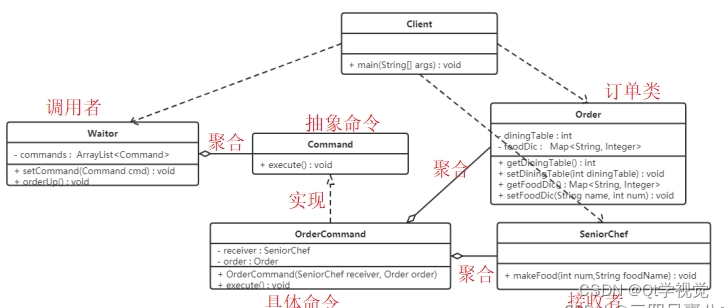
设计模式14、命令模式 Command
解释说明:命令模式(Command Pattern)是一种数据驱动的设计模式,它属于行为型模式。请求以命令的形式包裹在对象中,并传递给调用对象。调用对象寻找可以处理该命令的合适对象,并把该命令传给相应的对象&…...

【Go】excelize库实现excel导入导出封装(一),自定义导出样式、隔行背景色、自适应行高、动态导出指定列、动态更改表头
前言 最近在学go操作excel,毕竟在web开发里,操作excel是非常非常常见的。这里我选择用 excelize 库来实现操作excel。 为了方便和通用,我们需要把导入导出进行封装,这样以后就可以很方便的拿来用,或者进行扩展。 我参…...
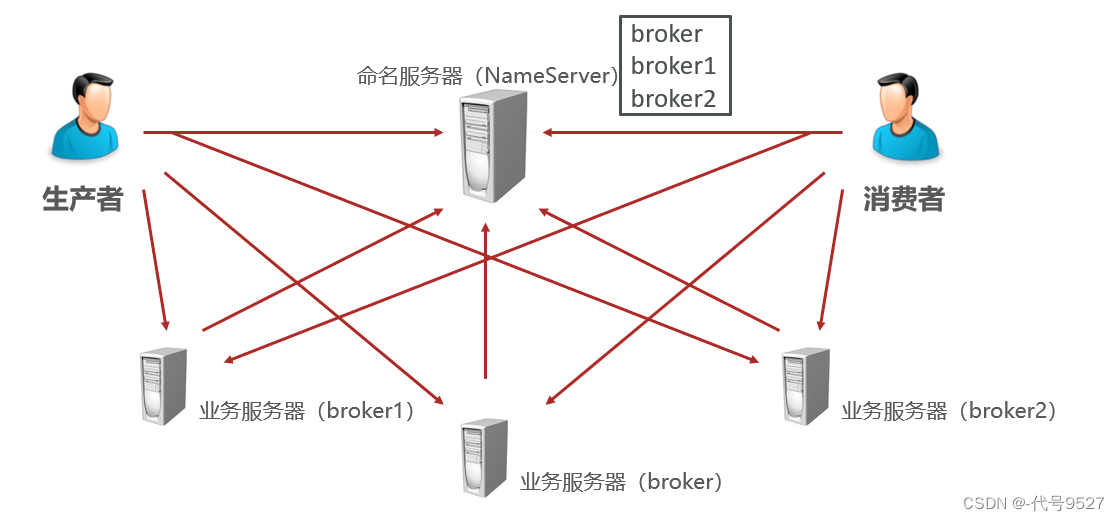
【开发篇】二十、SpringBoot整合RocketMQ
文章目录 1、整合2、消息的生产3、消费4、发送异步消息5、补充:安装RocketMQ 1、整合 首先导入起步依赖,RocketMQ的starter不是Spring维护的,这一点从starter的命名可以看出来(不是spring-boot-starter-xxx,而是xxx-s…...

OpenCV实现求解单目相机位姿
单目相机通过对极约束来求解相机运动的位姿。参考了ORBSLAM中单目实现的代码,这里用opencv来实现最简单的位姿估计. mLeftImg cv::imread(lImg, cv::IMREAD_GRAYSCALE); mRightImg cv::imread(rImg, cv::IMREAD_GRAYSCALE); cv::Ptr<ORB> OrbLeftExtractor …...

深入解析PostgreSQL:命令和语法详解及使用指南
文章目录 摘要引言基本操作安装与配置连接和退出 数据库操作创建数据库删除数据库切换数据库 表操作创建表删除表插入数据查询数据更新数据删除数据 索引和约束创建索引创建约束 用户管理创建用户授权用户修改用户密码 备份和恢复备份数据库恢复数据库 高级特性结语参考文献 摘…...

Elasticsearch数据搜索原理
Elasticsearch 是一个开源的、基于 Lucene 的分布式搜索和分析引擎,设计用于云计算环境中,能够实现实时的、可扩展的搜索、分析和探索全文和结构化数据。它具有高度的可扩展性,可以在短时间内搜索和分析大量数据。 Elasticsearch 不仅仅是一个…...
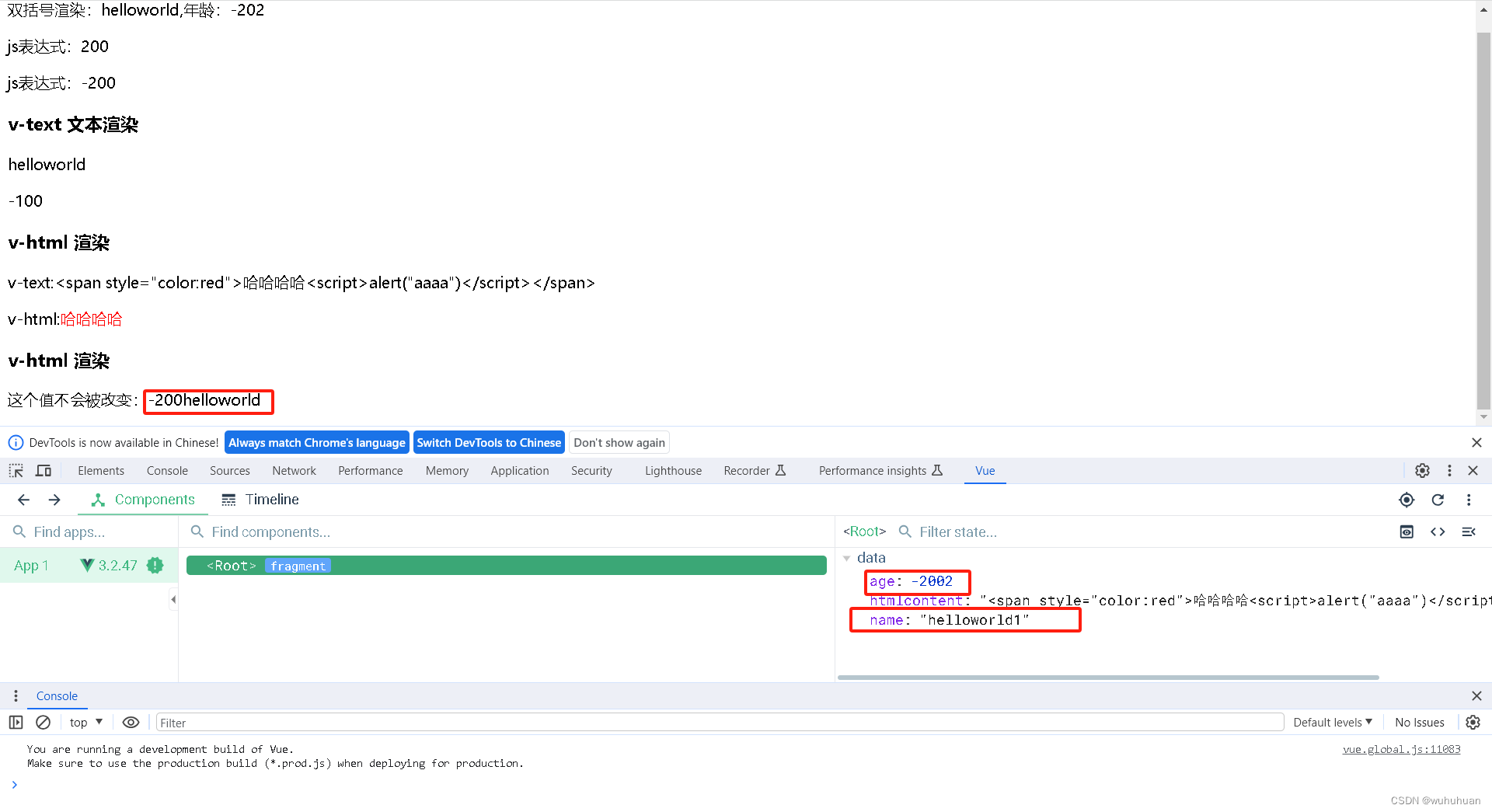
vue模版语法-{{}}/v-text/v-html/v-once
一、{{}}双括号:用于文本渲染 1、 {{变量名}}:data中返回对象的变量名 2、{{js表达式}}:可以直接进行js表达式处理 3、注意:双大括号中不要写等式书写 二、v-text 指令,用于文本渲染 1、为了解决双大括号渲染数据出现闪烁问题 三、v-cloak …...

前端埋点上传
没事看看: 从用户行为到数据:数据采集全景解析 | 人人都是产品经理 搭建前端监控,采集用户行为的 N 种姿势-前端监控设备 创业公司做数据分析(三)用户行为数据采集系统-CSDN博客...
)
第11章 Redis(一)
11.1 谈谈你对Redis的理解 难度:★★★ 重点:★★ 白话解析 对Redis的理解无非从三个方面去说一说:背景,是什么,特性。 背景:数据直接存磁盘太慢了,虽然MySQL用到了BufferPool等缓存,但是为了保证数据不丢失,MySQL采用的RedoLog依然要直接写磁盘。所以,数据的存储就…...

freertos信号量之二值信号量
freertos信号量之二值信号量 简介例程 简介 FreeRTOS的二值信号量(Binary Semaphore)是用于实现进程间同步和临界资源保护的重要工具。以下是一些二值信号量的常用函数及其说明: 1)xSemaphoreCreateBinary() 创建一个二值信号量…...
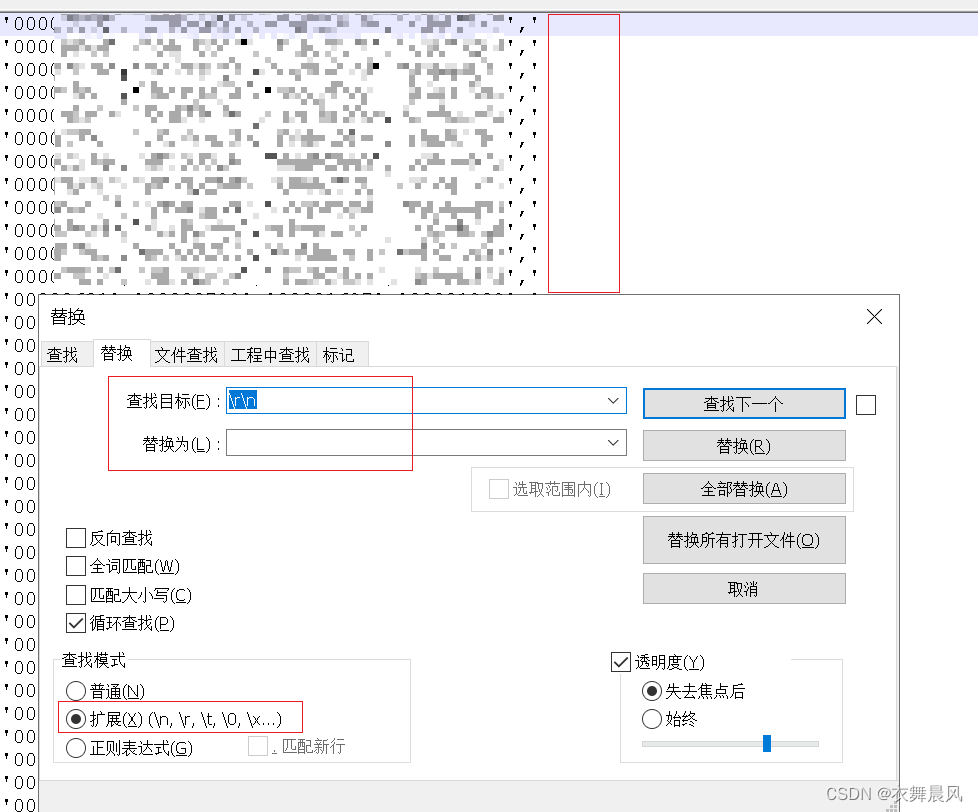
notepad++ 如何去除换行
选中下方的“扩展” “查找目标”输入:\r\n,替换为:空白 最后全部替换。...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

