代理IP与Socks5代理在多领域的卓越应用
随着数字化时代的到来,网络工程师在跨界电商、爬虫、出海业务、网络安全和游戏等多个领域中扮演着至关重要的角色。在这些领域中,代理IP与Socks5代理技术已经成为网络工程师的得力助手,本文将深入探讨它们在技术世界中的卓越应用。
1. 跨界电商:解锁全球市场的大门
跨界电商需要企业能够迅速扩展到不同国家和地区,而代理IP技术可帮助企业模拟不同地区的用户访问,更好地了解市场需求、竞争态势,从而优化产品和服务。此外,代理IP还可用于绕过地理位置限制,访问受限制的内容和服务,为企业拓展全球市场提供有力支持。
2. 爬虫应用:数据采集的得力工具
在信息时代,数据是企业决策的基石。爬虫应用需要频繁地访问各种网站,抓取数据,但频繁的请求可能导致IP被封禁。代理IP技术可以帮助分散请求,降低被封禁的风险,确保数据采集的稳定性和连续性。这对于市场研究、竞争情报收集以及战略规划至关重要。
3. 出海业务:连接世界的纽带
出海业务对网络工程师提出更高的网络性能和安全性要求。代理IP技术可用于确保稳定的全球连接,同时保护企业的数据隐私。通过使用代理IP,网络工程师可以轻松绕过地理位置限制,访问目标市场的特定内容和服务,促进出海业务的发展。
4. 网络安全:保护数字世界的城墙
网络工程师在网络安全领域发挥着关键作用。代理IP技术可以用于建立安全的通信通道,确保敏感数据的传输安全。同时,Socks5代理技术可绕过网络审查和防火墙,访问被封锁的网站和服务,提高网络的可访问性。这些技术为保护企业免受网络威胁提供了有力支持。
5. 游戏领域:提升游戏体验的关键
在游戏领域,网络工程师需要保障网络的稳定性和低延迟。Socks5代理技术帮助玩家降低游戏延迟,提高游戏体验。通过连接到最近的游戏服务器节点,玩家可以减少数据包传输时间,确保游戏的流畅性。
总结而言,代理IP与Socks5代理技术在多个领域中展现了卓越的应用潜力。它们为企业拓展市场、实现数据采集、扩展国际业务、保障网络安全和提升游戏体验提供了有力支持。网络工程师的任务是不断学习、创新和适应新的技术趋势,以满足不断增长的技术需求,确保网络的稳定性、数据的安全性以及用户体验的提升。在技术不断演进的时代,代理IP和Socks5代理技术将继续在各个领域中发挥其关键作用。
相关文章:

代理IP与Socks5代理在多领域的卓越应用
随着数字化时代的到来,网络工程师在跨界电商、爬虫、出海业务、网络安全和游戏等多个领域中扮演着至关重要的角色。在这些领域中,代理IP与Socks5代理技术已经成为网络工程师的得力助手,本文将深入探讨它们在技术世界中的卓越应用。 1. 跨界电…...
的?)
kafka怎么实现零拷贝(Zero-Copy)的?
Kafka 实现零拷贝(Zero-Copy)主要依赖于操作系统和底层网络库的支持,而不是特定的算法。这是因为零拷贝是一种优化数据传输的技术,通常是通过操作系统和硬件来实现的。以下是 Kafka 如何实现零拷贝的一般原理: 直接内存…...
函数-单行函数】)
Hive【Hive(四)函数-单行函数】
函数 函数简介 方便完成我们一些复杂的操作,就好像我们 Spark 中的 UDF 函数,避免用户反复写逻辑。 Hive 提供了大量的内置函数,主要可以分为以下几类: 单行函数聚合函数炸裂函数窗口函数 下面的命令可以查看内置函数的相关…...
C语言学生成绩录入系统
一、系统概述 该系统是一个由链表创建主菜单的框架,旨在快速创建学生成绩录入系统的主菜单结构。其主要任务包括: 实现链表的创建、插入和遍历功能,用于存储和展示学生成绩录入系统各个模块的菜单项。 2. 提供用户友好的主菜单界面…...
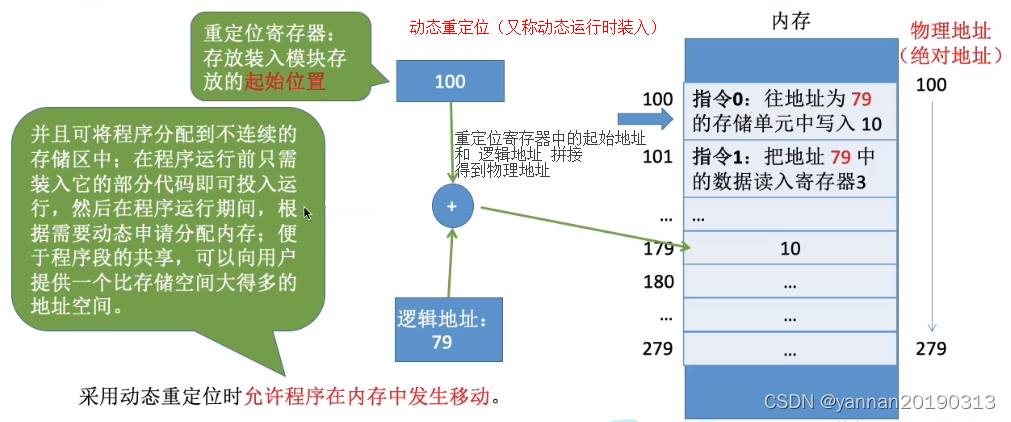
操作系统对内存的管理:分配与回收,虚拟内存,内存容量的扩充,内存保护,补充(链接方式、装入方式)
内存:即内存条,也称主存储器(简称主存),用于存放数据。 为了缓和CPU和外存(磁盘)的速度矛盾,外存的程序先放入内存才能被CPU处理。 内存地址从0开始,每个内存地址对应一…...
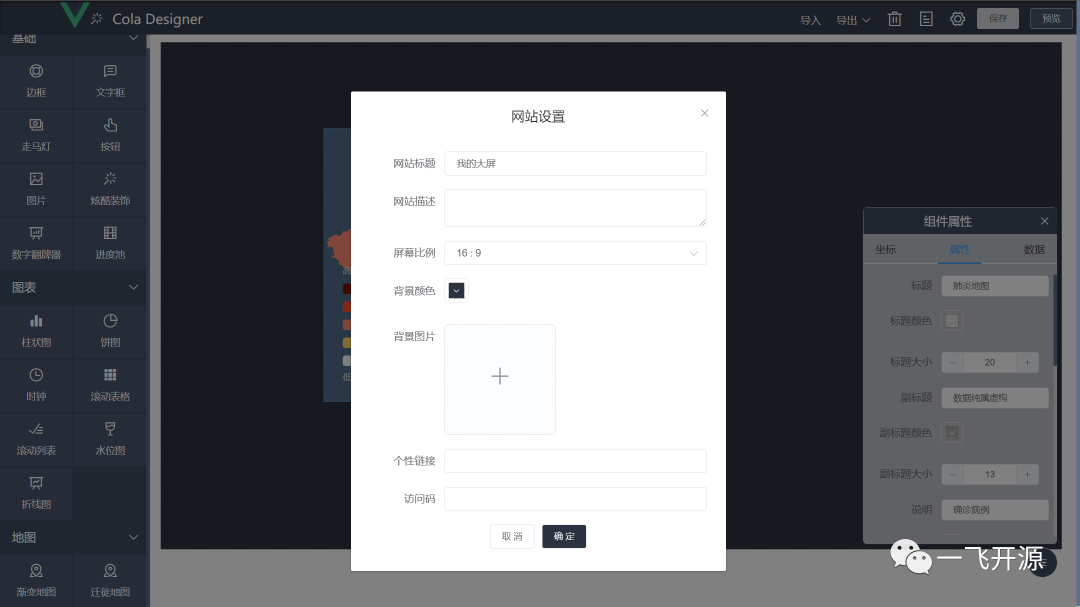
[开源]基于Vue的拖拽式数据报表设计器,为简化开发提高效率而生
一、开源项目简介 Cola-Designer 是一个 基于VUE,实现拖拽 配置方式生成数据大屏,为简化开发、提高效率而生。 二、开源协议 使用GPL-2.0开源协议 三、界面展示 概览 部分截图: 四、功能概述 特性 0 代码 实现完全拖拽 配置式生成…...
微信小程序——CSS3渐变
SS3 渐变(gradients)可以在两个或多个指定的颜色之间显示平稳的过渡。CSS3 定义了两种类型的渐变(gradients): 说明 1、线性渐变(Linear Gradients)- 向下/向上/向左/向右/对角方向࿱…...

CCF中国开源大会专访|毛晓光:“联合”是开源走向“共赢”的必由之路
受访嘉宾 | 毛晓光 记者 | 朱珂欣 2023 CCF 中国开源大会( CCF ChinaOSC )拟于 2023 年 10 月 21 日至 22 日在湖南省长沙市北辰国际会议中心召开。 作为第二届 CCF 中国开源大会,本届大会将组织特邀报告、高峰论坛和领域分论坛等不同类…...

多校联测11 8ady
题目大意 有一个排列 a 1 , a 2 , … , a n a_1,a_2,\dots,a_n a1,a2,…,an,我们现在进行如下操作: for(int i1;i<n-m1;i) sort(ai,aim);设最后的结果为 b 1 , b 2 , ⋯ , b n b_1,b_2,\cdots,b_n b1,b2,⋯,bn,求满足条件的…...
【软考】9.1 顺序表/链表/栈和队列
《线性结构》 顺序存储和链表存储 每个元素最多只有一个出度和一个入度,表现为一条线状链表存储结构:每个节点有两个域,即数据,指针域(指向下一个逻辑上相邻的节点) 时间复杂度:与其数量级成正…...

来 来 来 国家开放大学模拟题型 训练
试卷代号:2110 行政法与行政诉讼法 参考试题 一、单项选择题(每小题只有一项正确答案,请将正确答案的序号填在括号内。每小题2分,共20分) 1.下列案件中属于行政诉讼受案范围的是( )。 A.因人民政府对某工作人员的…...
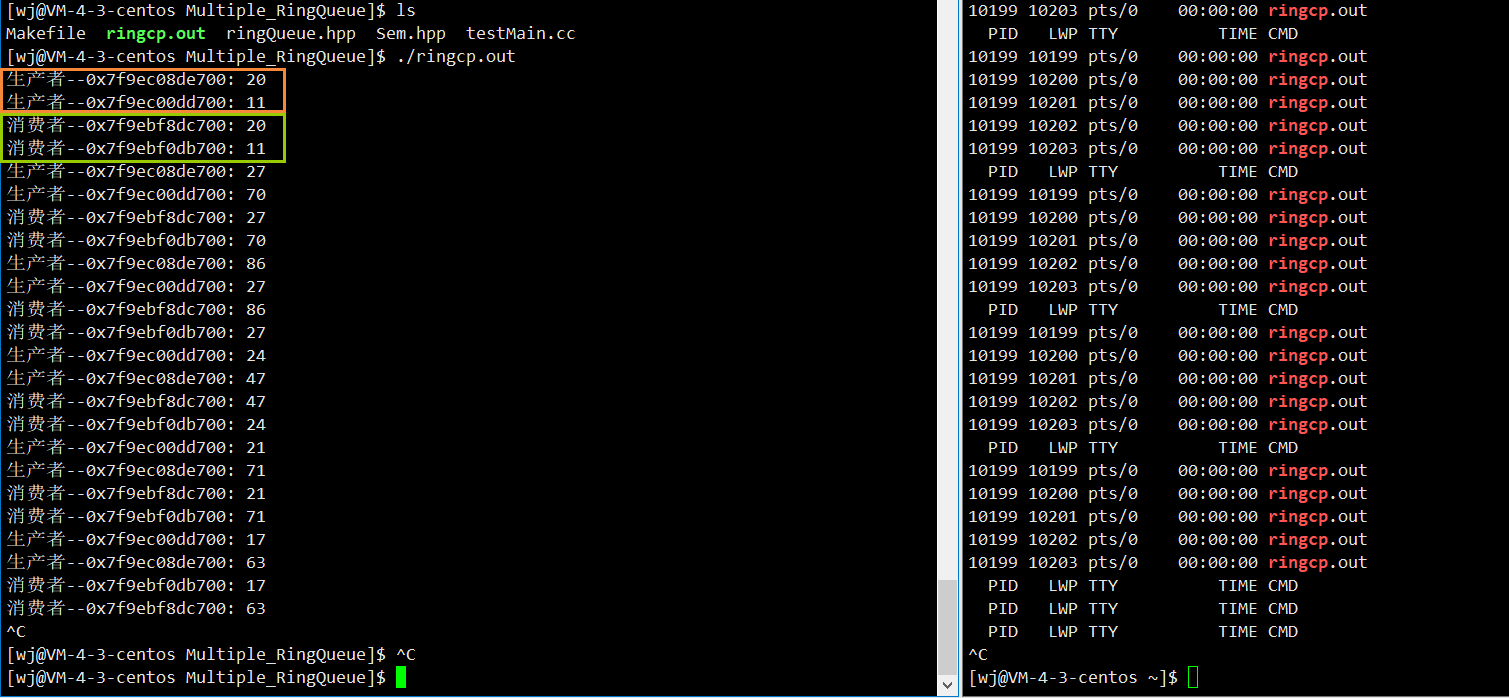
【ONE·Linux || 多线程(二)】
总言 多线程:生产者消费者模型与两种实现方式(条件变量、信号量)、线程池。 文章目录 总言4、生产者消费者模型4.1、基本概念4.2、基于BlockingQueue的生产者消费者模型(理解条件变量)4.2.1、单生产者单消费者模式&am…...

pandas.DataFrame.to_excel:在同一个sheet内追加数据
参考了这篇文章的方法 pandas to_excel:写入数据,在同一个sheet中追加数据,写入到多个sheet里,基本逻辑是: 通过数据框获取到该Excel表的行数 df_rows,然后将需要存储的数据,限制开始写入的行数,…...

基于卷积神经网络的图像识别技术研究与实践
基于卷积神经网络的图像识别技术研究与实践 卷积神经网络(CNN)是一种深度学习模型,它在图像识别领域取得了显著的成果。本文旨在探讨基于卷积神经网络的图像识别技术研究与实践。 一、卷积神经网络概述 卷积神经网络是一种深度学习模型&am…...

Linux防火墙之--SNAT和DNAT
1.SNAT是什么 SNAT又称源地址转换。源地址转换是内网地址向外访问时,发起访问的内网ip地址转换为指定的ip地址(可指定具体的服务以及相应的端口或端口范围),这可以使内网中使用保留ip地址的主机访问外部网络,即内网的多…...

Bean注入方式:@Autowired、@Resource的区别
Autowired 和 Resource 的区别是什么? Autowired 属于 Spring 内置的注解,默认的注入方式为 byType(根据类型进行匹配),也就是说会优先根据接口类型去匹配并注入 Bean (接口的实现类)。 这会有…...

软件设计原则 1小时系列 (C++版)
文章目录 前言基本概念 Design Principles⭐单一职责原则(SRP) Single Responsibility PrincipleCode ⭐里氏替换原则(LSP) Liskov Substitution PrincipleCode ⭐开闭原则(OCP) Open Closed PrincipleCode ⭐依赖倒置原则(DIP) Dependency Inversion PrincipleCode ⭐接口隔离…...
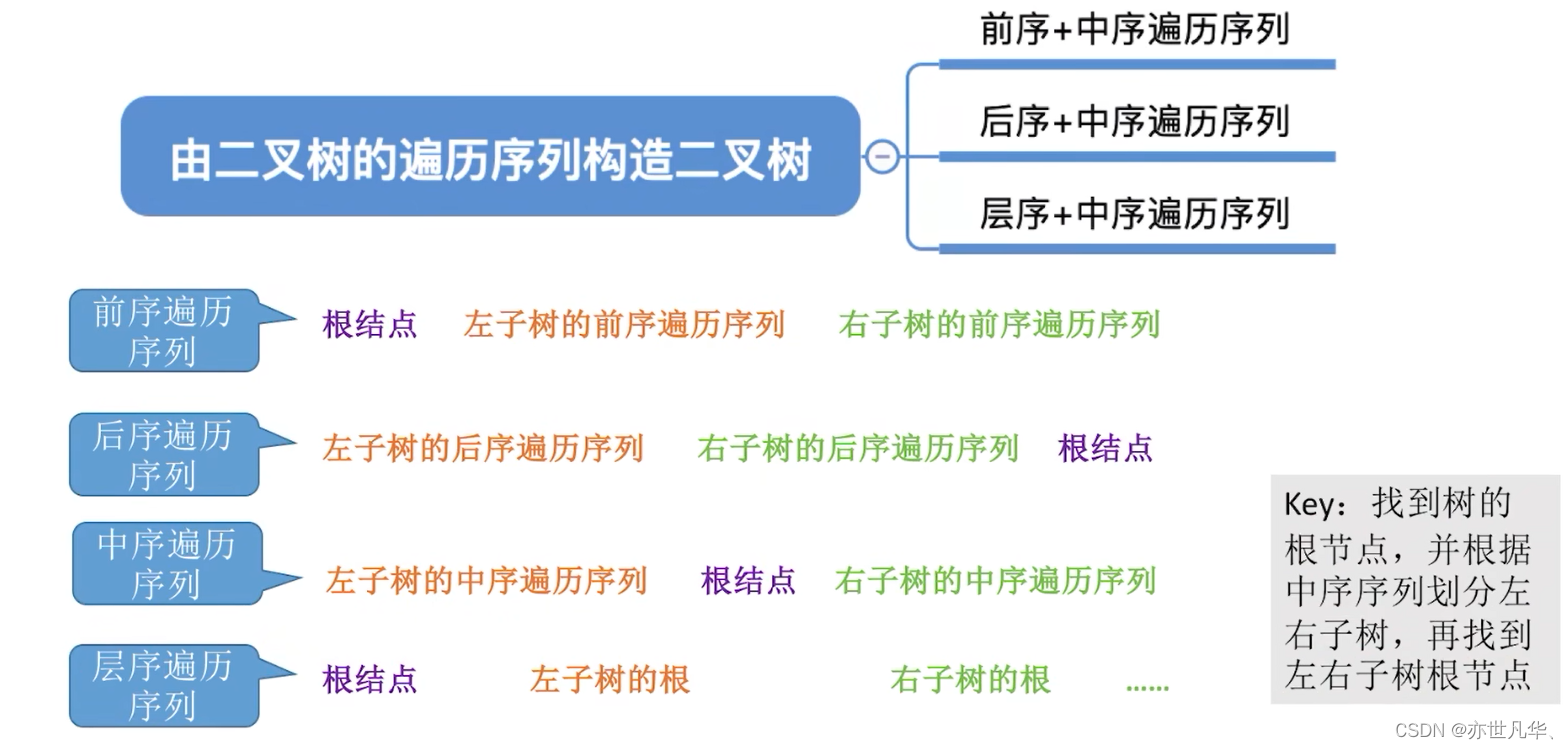
数据结构--》解锁数据结构中树与二叉树的奥秘(一)
数据结构中的树与二叉树,是在建立非线性数据结构方面极为重要的两个概念。它们不仅能够模拟出生活中各种实际问题的复杂关系,还常被用于实现搜索、排序、查找等算法,甚至成为一些大型软件和系统中的基础设施。 无论你是初学者还是进阶者&…...
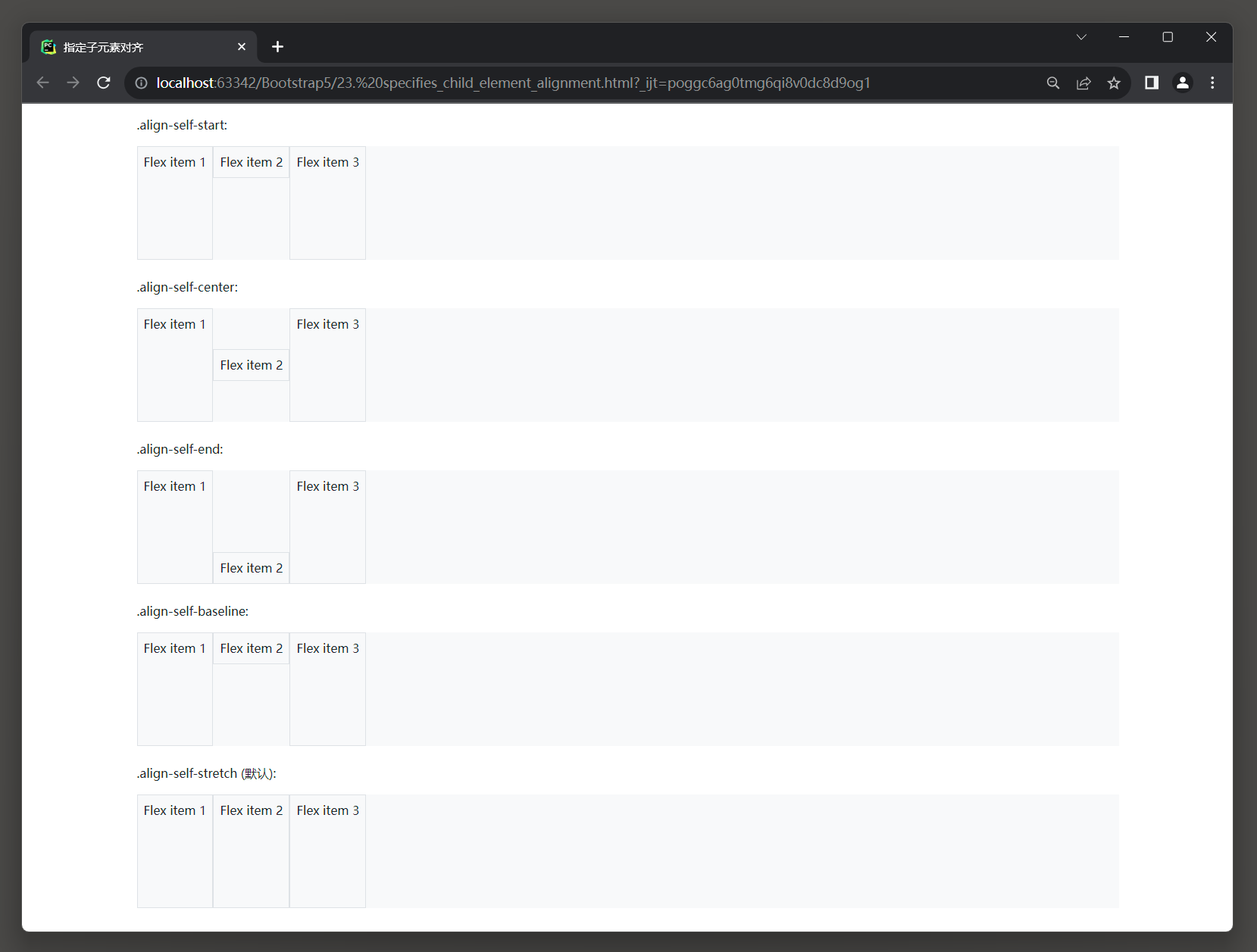
23.4 Bootstrap 框架5
1. 背景颜色 1.1 背景颜色样式 在Bootstrap 5中, 可以使用以下类来设置背景颜色: * 1. .bg-primary: 设置为主要的背景颜色(#007bff, 深蓝色). * 2. .bg-secondary: 设置为次要的背景颜色(#6c757d, 灰色). * 3. .bg-success: 设置为成功的背景颜色(#28a745, 绿色). * 4. …...
Spring源码解析——IOC属性填充
正文 doCreateBean() 主要用于完成 bean 的创建和初始化工作,我们可以将其分为四个过程: 最全面的Java面试网站 createBeanInstance() 实例化 beanpopulateBean() 属性填充循环依赖的处理initializeBean() 初始化 bean 第一个过程实例化 bean在前面一篇…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...
