多校联测11 8ady
题目大意
有一个排列 a 1 , a 2 , … , a n a_1,a_2,\dots,a_n a1,a2,…,an,我们现在进行如下操作:
for(int i=1;i<=n-m+1;i++) sort(a+i,a+i+m);
设最后的结果为 b 1 , b 2 , ⋯ , b n b_1,b_2,\cdots,b_n b1,b2,⋯,bn,求满足条件的 a a a中字典序第 k k k小的 a a a。
1 ≤ n ≤ 1 0 6 , m ≤ n , 1 ≤ k ≤ 1 0 18 1\leq n\leq 10^6,m\leq n,1\leq k\leq 10^{18} 1≤n≤106,m≤n,1≤k≤1018, b i b_i bi是 1 1 1到 n n n的一个排列。
题解
由题意可得 b i b_i bi是 a 1 , a 2 , … , a min ( i + m − 1 , n ) a_1,a_2,\dots,a_{\min(i+m-1,n)} a1,a2,…,amin(i+m−1,n)中,满足不在 b 1 , b 2 , … , b i − 1 b_1,b_2,\dots,b_{i-1} b1,b2,…,bi−1中的最小的数。
那么,当 b i − 1 > b i b_{i-1}>b_i bi−1>bi,就一定有 a i + m − 1 = b i a_{i+m-1}=b_i ai+m−1=bi。
把这些已经确定的 b i b_i bi去掉,剩下的问题等价于 n n n变小, m , k m,k m,k不变, b i = i b_i=i bi=i的子问题。
下面,我们假设 b i = i b_i=i bi=i。
考虑从小到大将每一个 i i i填入 a a a中,易得 i i i需要填在 [ 1 , min ( i + m − 1 , n ) ] [1,\min(i+m-1,n)] [1,min(i+m−1,n)]中任意没填过的位置,那么填 i i i的方案数为 min ( m , n − i + 1 ) \min(m,n-i+1) min(m,n−i+1)。
然而,因为方案数很大,而 k k k相对没那么大,所以 a a a有一个前缀都满足 a i = i a_i=i ai=i。
设 f i f_i fi表示满足上面条件的前缀为 n − i n-i n−i,也就是后面有最多 i i i个数不满足,那么
f i = f i − 1 × min ( m , i ) f_i=f_{i-1}\times \min(m,i) fi=fi−1×min(m,i)
当 m = 1 m=1 m=1时,显然只有一个答案。因为保证有解,这种情况下 k = 1 k=1 k=1。
当 m > 1 m>1 m>1时, f i ≥ 2 i − 1 f_i\geq 2^{i-1} fi≥2i−1,可得 f 62 ≥ k f_{62}\geq k f62≥k
那么,我们只需取最后 min ( n , 62 ) \min(n,62) min(n,62)个位置,后面用一个状压维护状态,再枚举每一位填什么即可。细节见代码。
时间复杂度为 O ( n + v 3 ) O(n+v^3) O(n+v3),其中 v = min ( n , 62 ) v=\min(n,62) v=min(n,62)。
code
#include<bits/stdc++.h>
using namespace std;
int n,m,a[1000005],b[1000005],c[1000005],num[1000005],z[1000005];
long long k;
long long gt(int t,int w,long long now){long long re=1;for(int i=1;i<=t;i++){if((now>>i-1)&1){if(re>k/(min(i+m-1,t)-w)+1) return k+1;re=re*(min(i+m-1,t)-w);if(re>k) return k+1;++w;}}return re;
}
void dd(int l,int t){long long now=(1ll<<t)-1;for(int i=1;i<=l-t;i++) c[i]=num[i];for(int i=t;i>=1;i--){for(int j=1;j<=t;j++){if((now>>j-1)&1){long long vt=gt(t,t-i+1,now^(1ll<<j-1));if(k>=vt) k-=vt;else{c[l-i+1]=num[l-t+j];now^=(1ll<<j-1);break;}}}}
}
int main()
{scanf("%d%d%lld",&n,&m,&k);--k;for(int i=1;i<=n;i++){scanf("%d",&b[i]);}int lst=b[1],cnt=0;for(int i=2;i<=n;i++){if(lst>b[i]){a[i+m-1]=b[i];z[b[i]]=1;}else lst=b[i];}for(int i=1;i<=n;i++){if(!z[i]) num[++cnt]=i;}dd(cnt,min(cnt,62));int now=1;for(int i=1;i<=n;i++){if(!a[i]){a[i]=c[now];++now;}printf("%d ",a[i]);}return 0;
}
相关文章:

多校联测11 8ady
题目大意 有一个排列 a 1 , a 2 , … , a n a_1,a_2,\dots,a_n a1,a2,…,an,我们现在进行如下操作: for(int i1;i<n-m1;i) sort(ai,aim);设最后的结果为 b 1 , b 2 , ⋯ , b n b_1,b_2,\cdots,b_n b1,b2,⋯,bn,求满足条件的…...
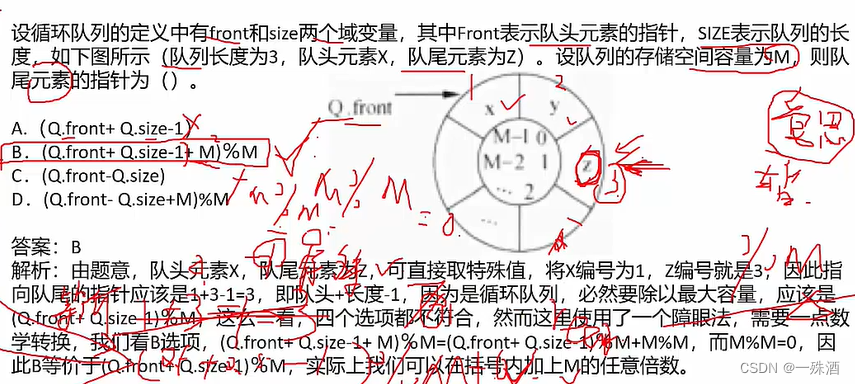
【软考】9.1 顺序表/链表/栈和队列
《线性结构》 顺序存储和链表存储 每个元素最多只有一个出度和一个入度,表现为一条线状链表存储结构:每个节点有两个域,即数据,指针域(指向下一个逻辑上相邻的节点) 时间复杂度:与其数量级成正…...

来 来 来 国家开放大学模拟题型 训练
试卷代号:2110 行政法与行政诉讼法 参考试题 一、单项选择题(每小题只有一项正确答案,请将正确答案的序号填在括号内。每小题2分,共20分) 1.下列案件中属于行政诉讼受案范围的是( )。 A.因人民政府对某工作人员的…...
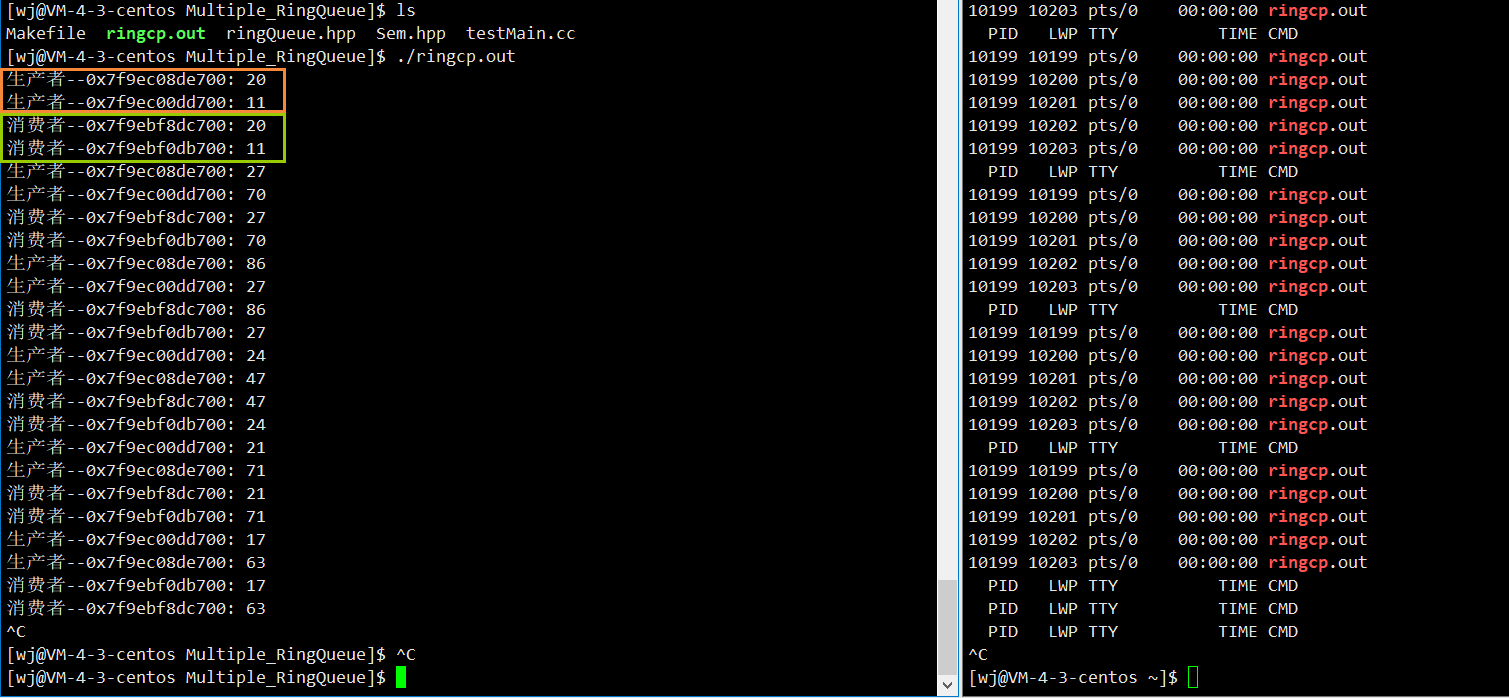
【ONE·Linux || 多线程(二)】
总言 多线程:生产者消费者模型与两种实现方式(条件变量、信号量)、线程池。 文章目录 总言4、生产者消费者模型4.1、基本概念4.2、基于BlockingQueue的生产者消费者模型(理解条件变量)4.2.1、单生产者单消费者模式&am…...

pandas.DataFrame.to_excel:在同一个sheet内追加数据
参考了这篇文章的方法 pandas to_excel:写入数据,在同一个sheet中追加数据,写入到多个sheet里,基本逻辑是: 通过数据框获取到该Excel表的行数 df_rows,然后将需要存储的数据,限制开始写入的行数,…...

基于卷积神经网络的图像识别技术研究与实践
基于卷积神经网络的图像识别技术研究与实践 卷积神经网络(CNN)是一种深度学习模型,它在图像识别领域取得了显著的成果。本文旨在探讨基于卷积神经网络的图像识别技术研究与实践。 一、卷积神经网络概述 卷积神经网络是一种深度学习模型&am…...

Linux防火墙之--SNAT和DNAT
1.SNAT是什么 SNAT又称源地址转换。源地址转换是内网地址向外访问时,发起访问的内网ip地址转换为指定的ip地址(可指定具体的服务以及相应的端口或端口范围),这可以使内网中使用保留ip地址的主机访问外部网络,即内网的多…...

Bean注入方式:@Autowired、@Resource的区别
Autowired 和 Resource 的区别是什么? Autowired 属于 Spring 内置的注解,默认的注入方式为 byType(根据类型进行匹配),也就是说会优先根据接口类型去匹配并注入 Bean (接口的实现类)。 这会有…...

软件设计原则 1小时系列 (C++版)
文章目录 前言基本概念 Design Principles⭐单一职责原则(SRP) Single Responsibility PrincipleCode ⭐里氏替换原则(LSP) Liskov Substitution PrincipleCode ⭐开闭原则(OCP) Open Closed PrincipleCode ⭐依赖倒置原则(DIP) Dependency Inversion PrincipleCode ⭐接口隔离…...
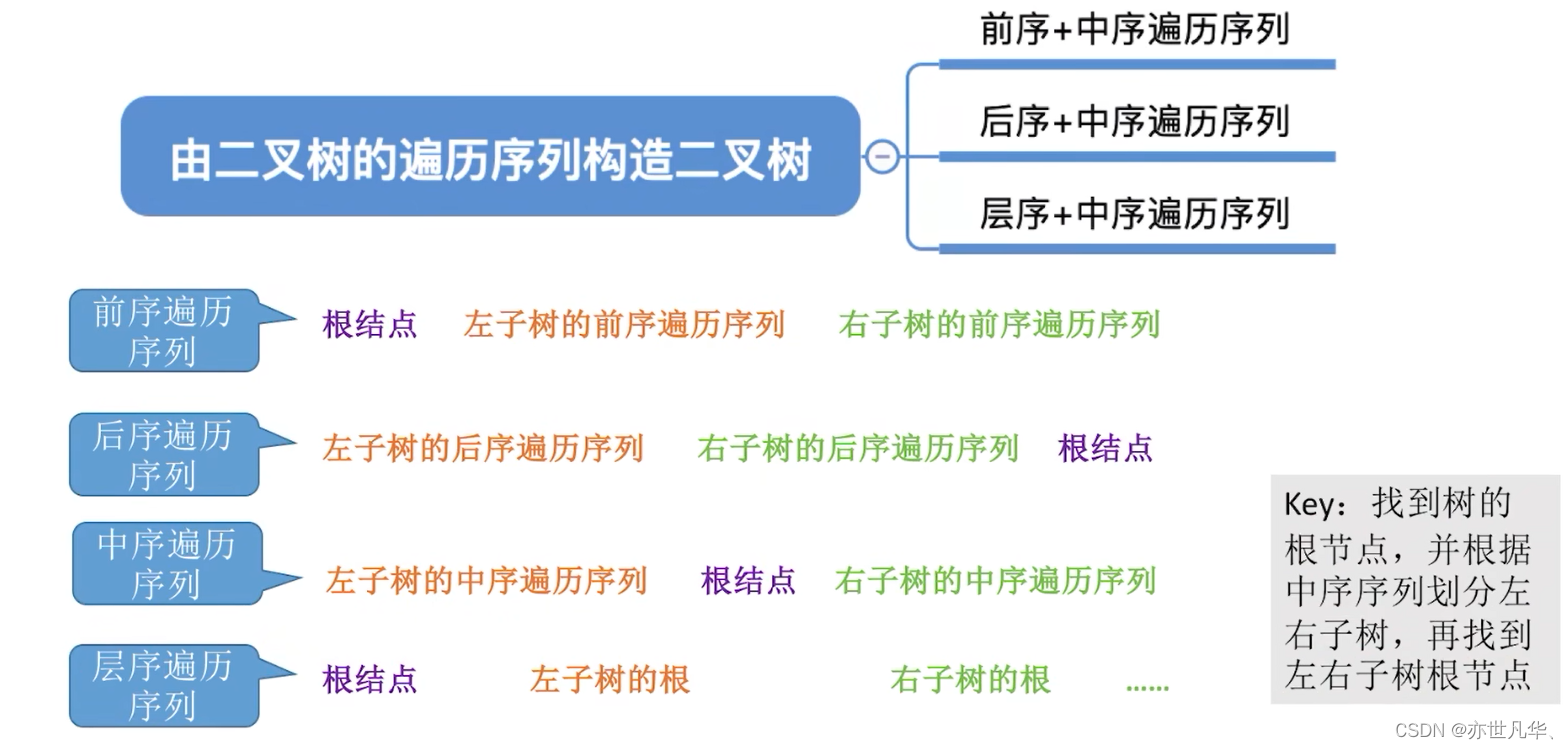
数据结构--》解锁数据结构中树与二叉树的奥秘(一)
数据结构中的树与二叉树,是在建立非线性数据结构方面极为重要的两个概念。它们不仅能够模拟出生活中各种实际问题的复杂关系,还常被用于实现搜索、排序、查找等算法,甚至成为一些大型软件和系统中的基础设施。 无论你是初学者还是进阶者&…...
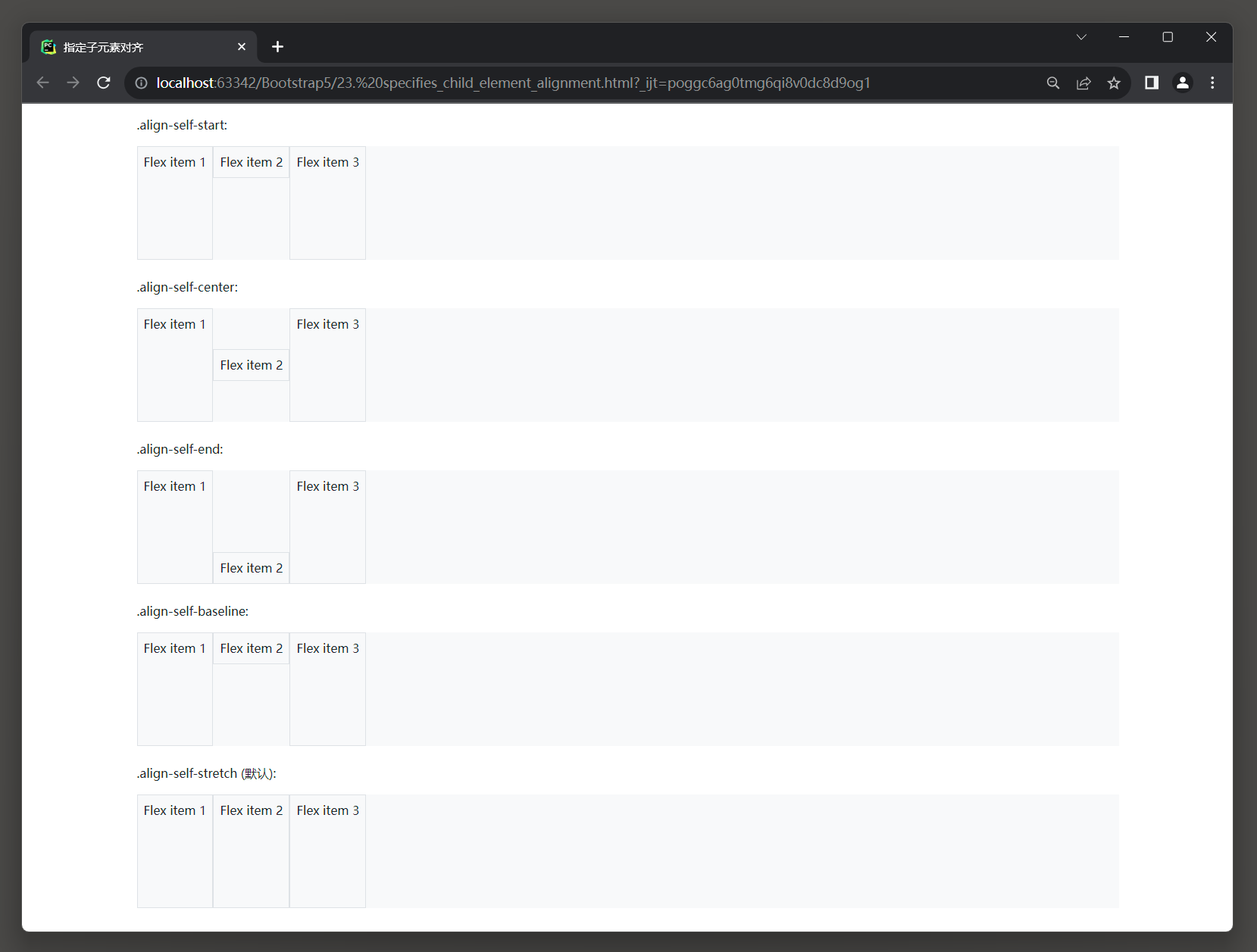
23.4 Bootstrap 框架5
1. 背景颜色 1.1 背景颜色样式 在Bootstrap 5中, 可以使用以下类来设置背景颜色: * 1. .bg-primary: 设置为主要的背景颜色(#007bff, 深蓝色). * 2. .bg-secondary: 设置为次要的背景颜色(#6c757d, 灰色). * 3. .bg-success: 设置为成功的背景颜色(#28a745, 绿色). * 4. …...
Spring源码解析——IOC属性填充
正文 doCreateBean() 主要用于完成 bean 的创建和初始化工作,我们可以将其分为四个过程: 最全面的Java面试网站 createBeanInstance() 实例化 beanpopulateBean() 属性填充循环依赖的处理initializeBean() 初始化 bean 第一个过程实例化 bean在前面一篇…...

寒露到了,冬天还会远吗?
寒露惊秋晚,朝看菊渐黄。 日复一日间,光影如梭,我们便很快将告别了秋高气爽,白日将变得幽晦, 天寒夜长,风气萧索,雾结烟愁。 还没好好体会秋高气爽,寒露就到了。 今天晚上9点多,我们…...

科普②| 大数据有什么用?大数据技术的应用领域有哪些?
1、提供个性服务很多人觉得大数据好像离我们很远,其实我们在日常所使用的智能设备,就需要大数据的帮助。比如说我们运动时候戴的运动手表或者是运动手环,就可以在我们平时运动的时候,帮助我们采集运动数据及热量消耗情况。进入睡眠…...

golang的切片使用总结二
如果没看golang切片的第一篇总结博客 golang的切片使用总结一-CSDN博客 ,请浏览之 举例9:make([]int, a, b)后访问下标a的元素 s : make([]int, 10, 12) v : s[10] fmt.Printf("v:%v", v) 打印结果: panic: runtime error: index …...
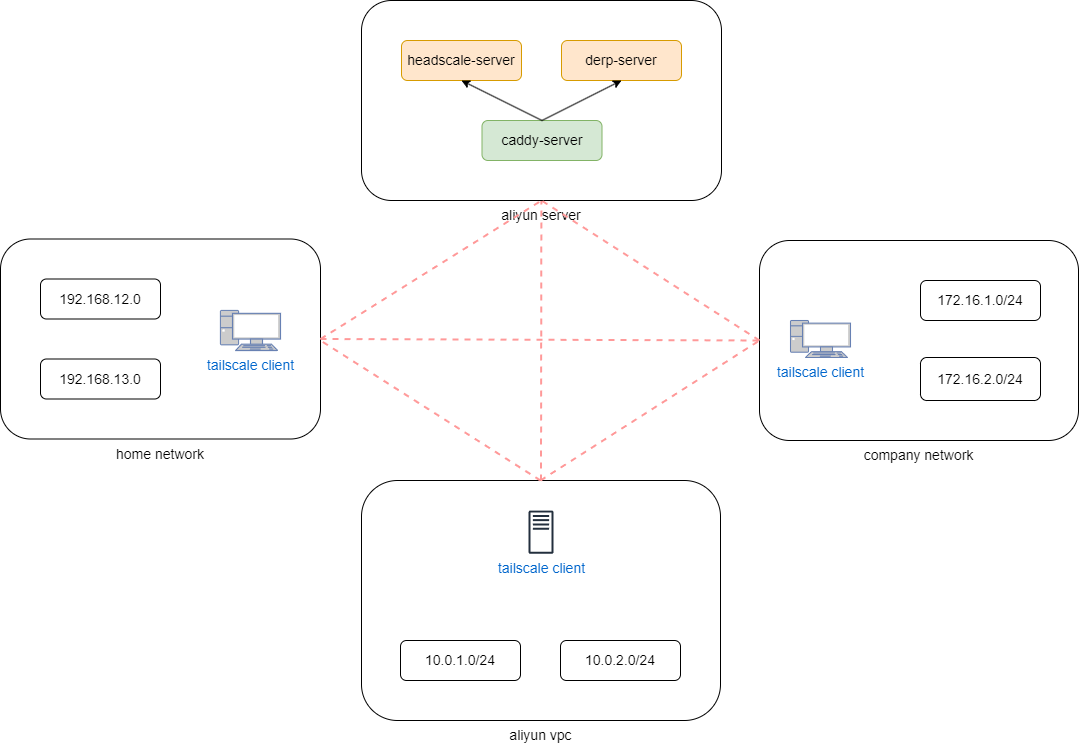
tailscale自建headscale和derp中继
tailscale derp中继服务简介 tailscale是一个基于WireGuard的零配置软件,它可以轻松地在多台设备之间建立点对点加密连接。 derp服务器是tailscale网络的重要组成部分。它作为tailscale客户端之间的中继,帮助客户端找到并连接到其他客户端设备。 但Tailscale 官方…...
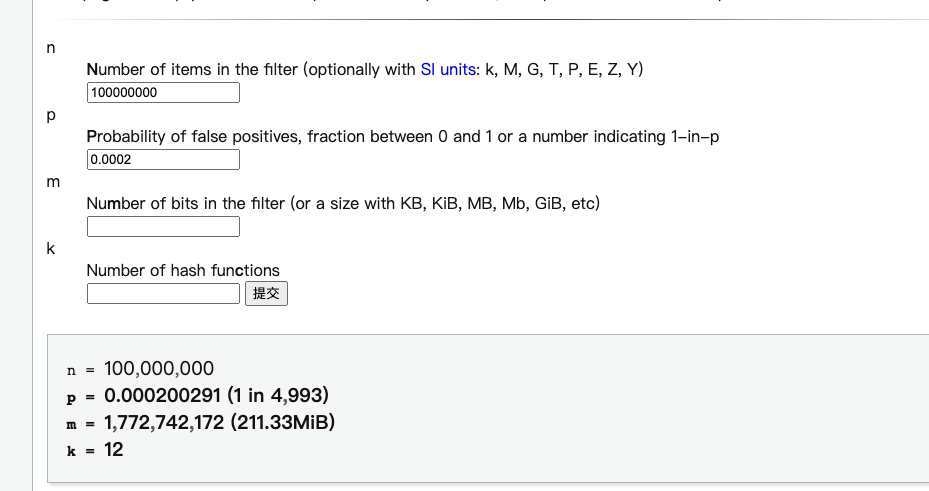
布隆过滤器的使用
布隆过滤器简介 Bloom Filter(布隆过滤器)是一种多哈希函数映射的快速查找算法。它是一种空间高效的概率型数据结构,通常应用在一些需要快速判断某个元素是否属于集合,但是并不严格要求100%正确的场合。 布隆过滤器的优势在于,利用很少的空…...

Web开发-单例模式
目录 单例模式介绍代码实现单例模式 单例模式介绍 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点。单例模式可以通过private属性实现。通过将类的构造函数设为private,可以防止类在外部被实例化。单例模式通…...
MySQL:温备份和恢复-mysqldump (4)
介绍 温备:同样是在数据库运行的时候进行备份的,但对当前数据库的操作会产生影响。(只可以读操作,不可以写操作) 温备份的优点: 1.可在表空间或数据文件级备份,备份时间短。 2.备份时数据库依然…...
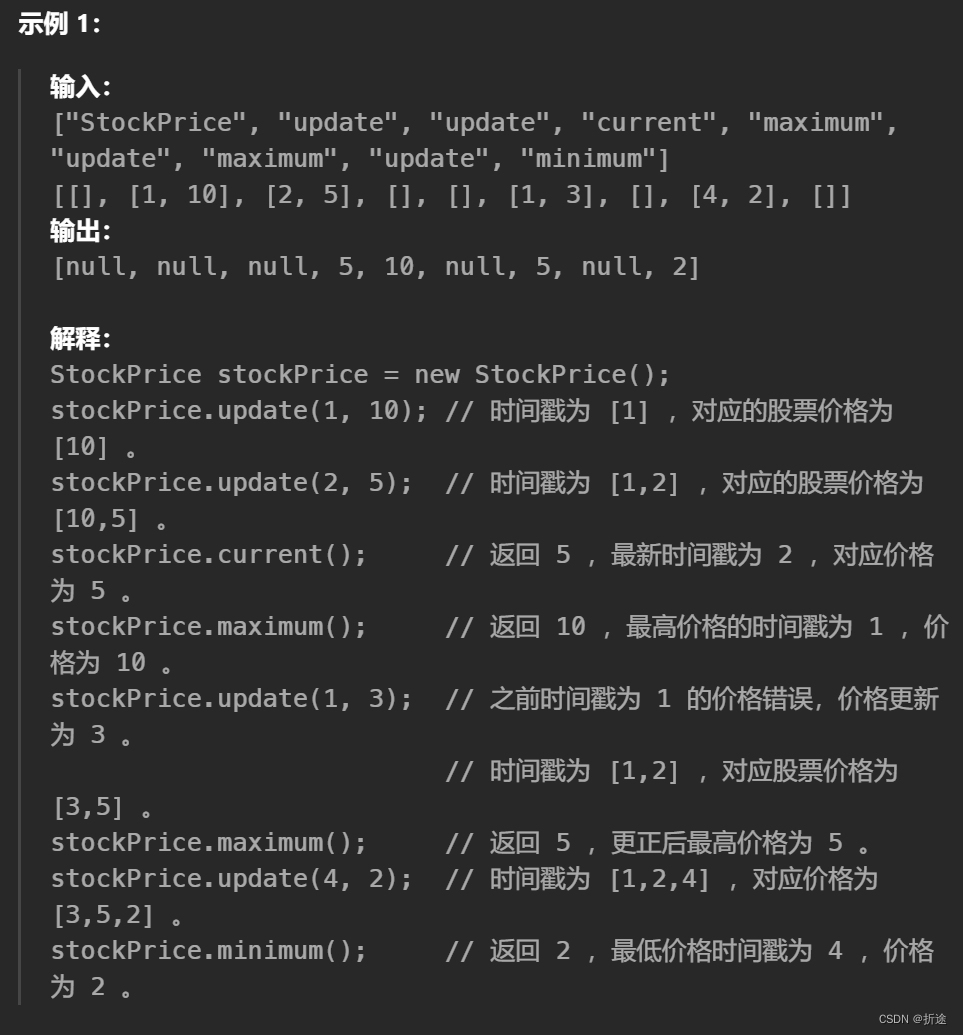
【力扣每日一题】2023.10.8 股票价格波动
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题是程序设计题,要我们实现一个类,一共是四个功能,第一个是给一个时间戳和价格,表示该…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
