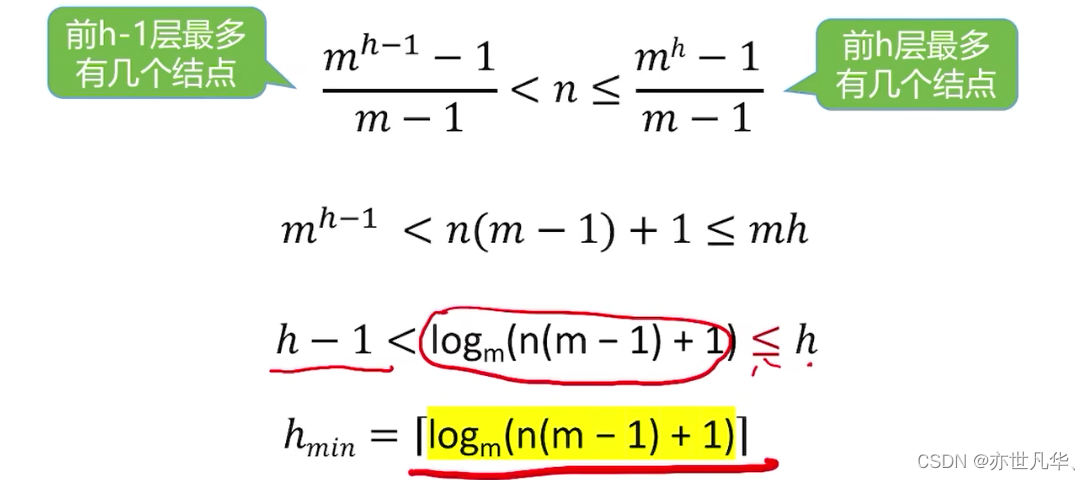数据结构--》解锁数据结构中树与二叉树的奥秘(一)
数据结构中的树与二叉树,是在建立非线性数据结构方面极为重要的两个概念。它们不仅能够模拟出生活中各种实际问题的复杂关系,还常被用于实现搜索、排序、查找等算法,甚至成为一些大型软件和系统中的基础设施。
无论你是初学者还是进阶者,本文将为你提供简单易懂、实用可行的知识点,帮助你更好地掌握树和二叉树在数据结构和算法中的重要性,进而提升算法解题的能力。接下来让我们开启数据结构与算法的奇妙之旅吧。
目录
树和森林的概念
树的常考性质
二叉树的定义及其性质
二叉树的表示
二叉树遍历
树和森林的概念
树的定义:树是一种非线性的数据结构,它由节点(node)和边(edge)组成。树的基本概念是以层次结构来组织和表示数据。
在树中,有一个特殊的节点被称为根节点(root),它是树的顶层节点,所有其他节点都直接或间接地与根节点相连。除了根节点外,每个节点可以有零个或多个子节点(child),子节点又可以有自己的子节点,形成了树的分支结构。没有子节点的节点被称为叶节点(leaf)或叶子节点,它们位于树的最底层。节点之间的连接称为边,边描述了节点之间的关系。每个节点可以有零条到多条边连接到其子节点。任意两个节点之间都存在唯一的路径,通过路径可以从一个节点到达另一个节点。
树的结构具有以下特点:
- 一个树可以由零个或多个节点组成。
- 有且只有一个根节点,它是树的起点。
- 每个节点可以有零个或多个子节点。
- 节点之间通过边相连,形成层次结构。
- 每个节点除了根节点外,都有且只有一个父节点。

树的基本术语:
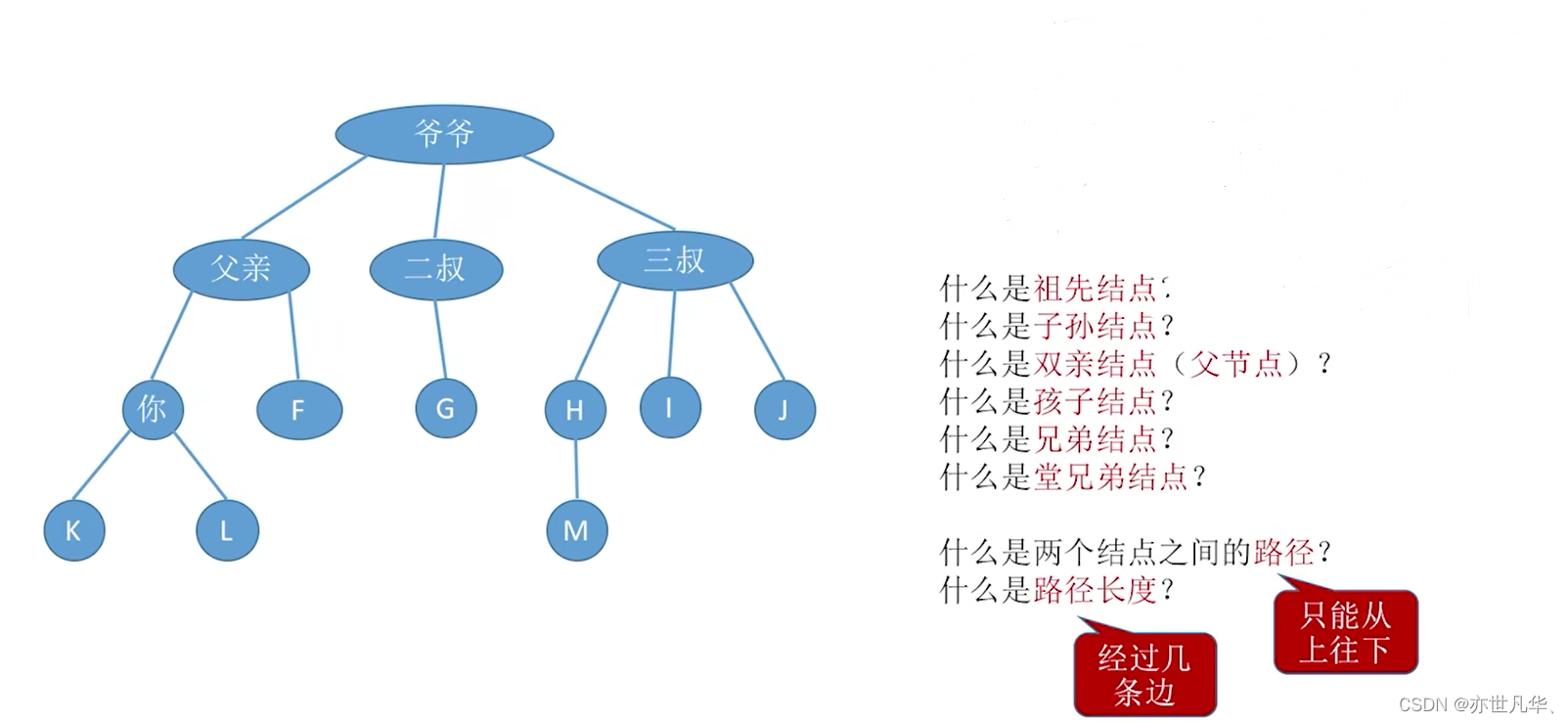
结点之间的关系描述
根节点(Root Node):树的顶层节点称为根节点。根节点是树的起点,它没有父节点,其他所有节点都直接或间接地与根节点相连。
祖先节点(Ancestor Node):对于一个节点,它的所有上级节点(包括父节点、父节点的父节点等等)都被称为该节点的祖先节点。
子孙节点(Descendant Node):对于一个节点,它的所有下级节点(包括子节点、子节点的子节点等等)都被称为该节点的子孙节点。
父节点(Parent Node):一个节点的直接上一级节点称为其父节点。每个节点都可以有零个或多个子节点,但只能有一个父节点(除了根节点)。
子节点(Child Node):一个节点直接连接的下一级节点称为其子节点。一个节点可以有零个或多个子节点。
兄弟节点(Sibling Node):具有相同父节点的节点称为兄弟节点。兄弟节点在同一层级上。
叶节点(Leaf Node):也称为叶子节点,是没有子节点的节点,位于树的最底层。
层级(Level):根节点在第一层,其直接子节点在第二层,以此类推。一个节点所在的层级数即为该节点的层级。
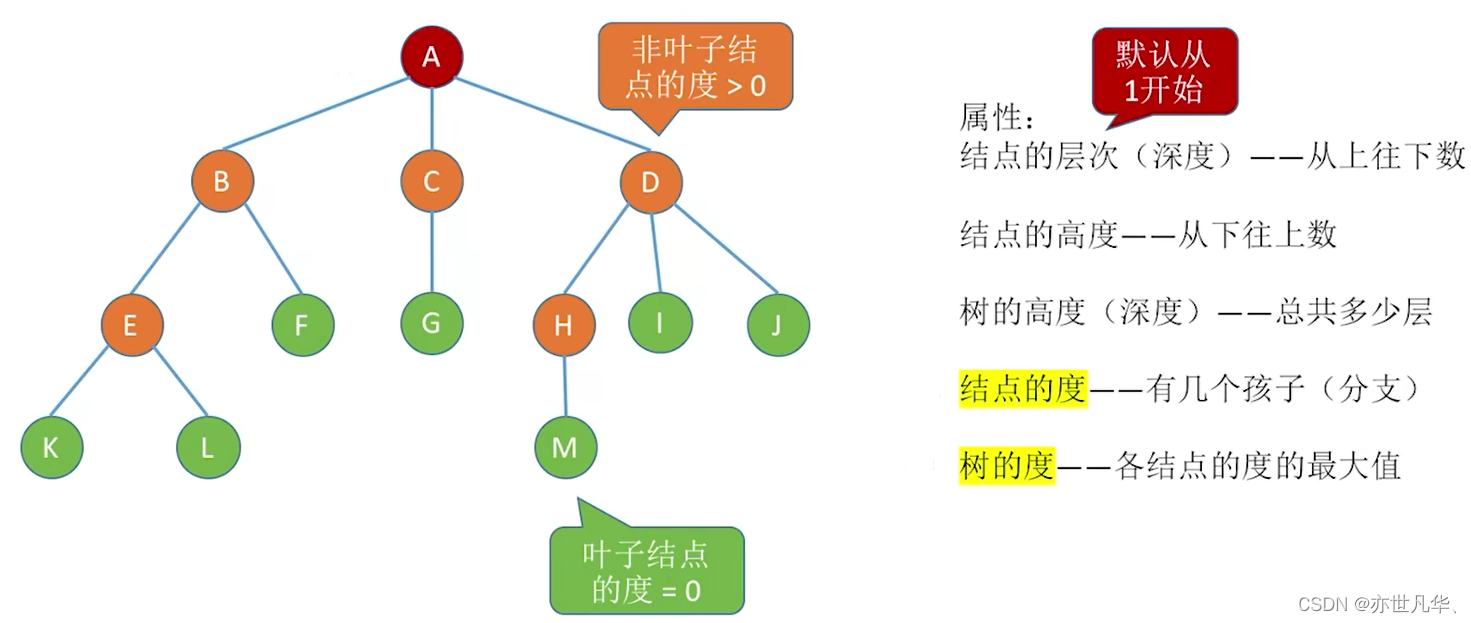
结点、树的属性描述
节点值(Node Value):每个节点都可以携带一个值或数据,表示该节点所代表的实际含义或信息。
节点深度(Node Depth):节点深度指的是该节点到根节点的路径长度,即从根节点到该节点所经过的边的数量。根节点的深度为0。
节点高度(Node Height):节点高度指的是该节点到其最远叶节点的路径长度,即从该节点到达最远叶节点所经过的边的数量。叶节点的高度为0。
子树(Subtree):对于一个树中的节点,可以以该节点为根构成的子树称为该节点的子树。
树的大小(Tree Size):指的是树中包含的所有节点的总数。
树的高度(Tree Height):指的是树中任意节点的高度的最大值。也可以理解为从根节点到最远叶节点的路径长度的最大值。
有序树、无序树
有序树(Ordered Tree):有序树是指树中的子节点之间存在明确的顺序关系。在有序树中,每个子节点都有一个明确定义的位置,在遍历和表示树的时候需要按照顺序来考虑。例如,家谱树中的兄弟姐妹一般按照他们出生的先后顺序排列。
无序树(Unordered Tree):无序树是指树中的子节点之间没有明确的顺序关系。在无序树中,所有子节点都是平等的,没有先后之分。例如,文件系统中的目录结构就是一种无序树,其中的各个子目录之间没有特定的顺序。
有序树和无序树的区别在于子节点的排列方式。在有序树中,子节点的顺序很重要,会影响到树的结构和含义;而在无序树中,子节点的顺序并不重要,只需要知道它们是该节点的子节点即可。

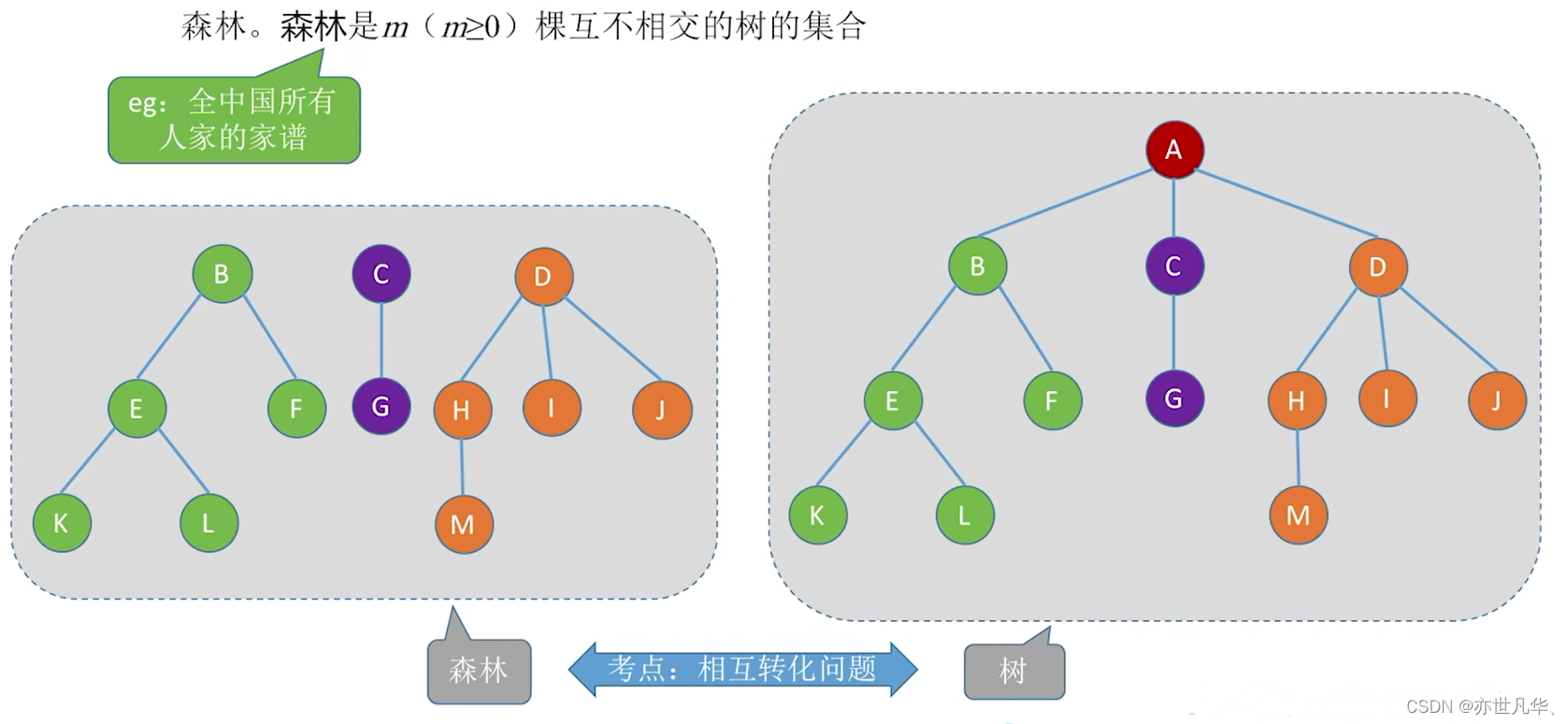
森林
森林(Forest)是指由多棵树(Tree)组成的集合。简单来说,森林可以看作是多个独立的树的集合。
森林的特点在于其中的树之间是相互独立的,彼此之间没有直接的连接或关系。每棵树都可以独立地进行遍历和操作。
需要注意的是,森林和树的层次结构是不同的概念。树是一种层次结构,它具有唯一的根节点和从根节点到其他节点的确定路径;而森林则是多个独立的树的集合,在森林中任意两棵树之间没有直接的联系。
树的抽象数据类型:
树的抽象数据类型定义了对树进行操作的基本操作集合,包括以下常见操作:
1)创建树:创建一个空的树数据结构。
2)插入节点:在树中插入一个新节点,并建立节点之间的关系。
3)删除节点:从树中删除指定的节点,并调整节点之间的关系。
4)遍历树:按照特定的顺序访问树中的节点,例如先序遍历、中序遍历、后序遍历等。
5)查找节点:在树中查找指定的节点。
6)获取树的属性:获取树的高度、节点个数、根节点等属性信息。
树的抽象数据类型并不关注具体的实现方式,而是定义了可以对树进行的操作以及这些操作的预期行为。
回顾重点,其主要内容整理成如下内容:
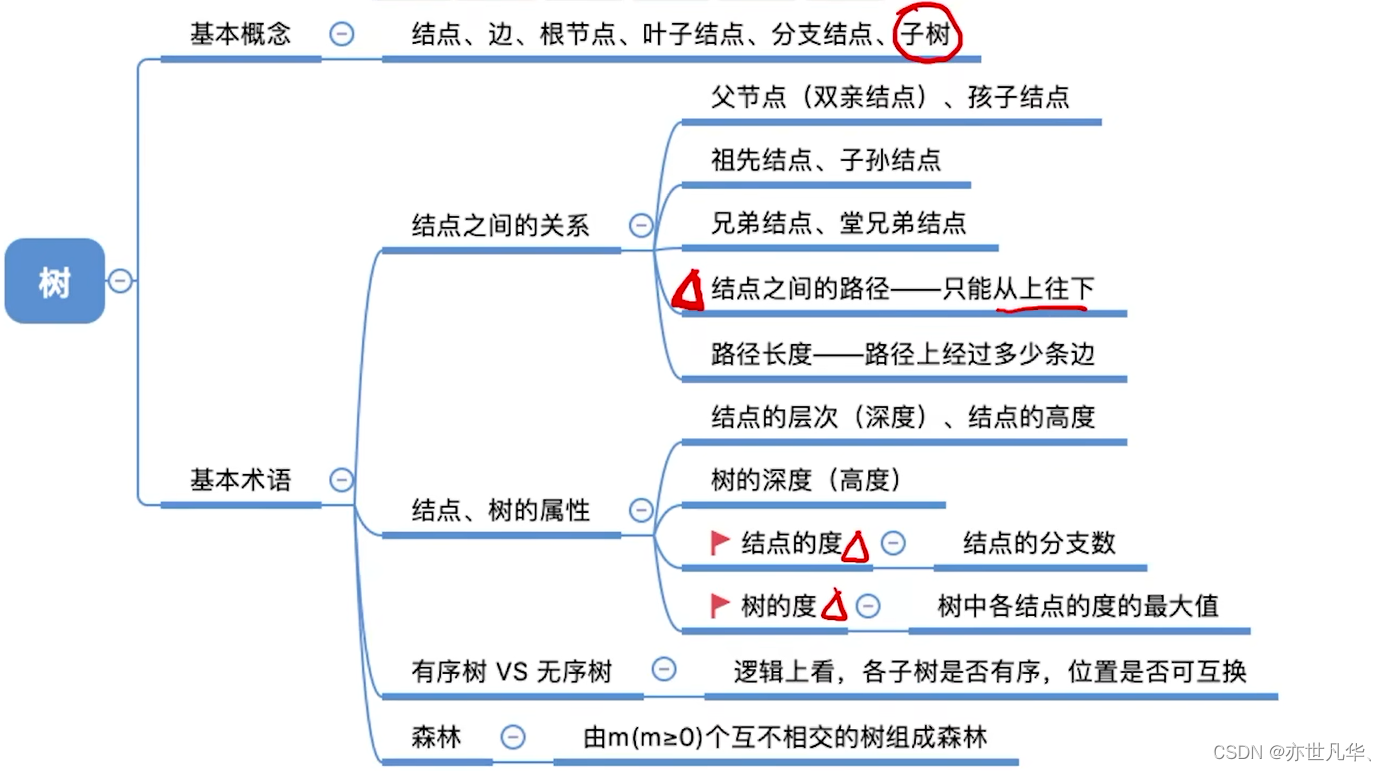
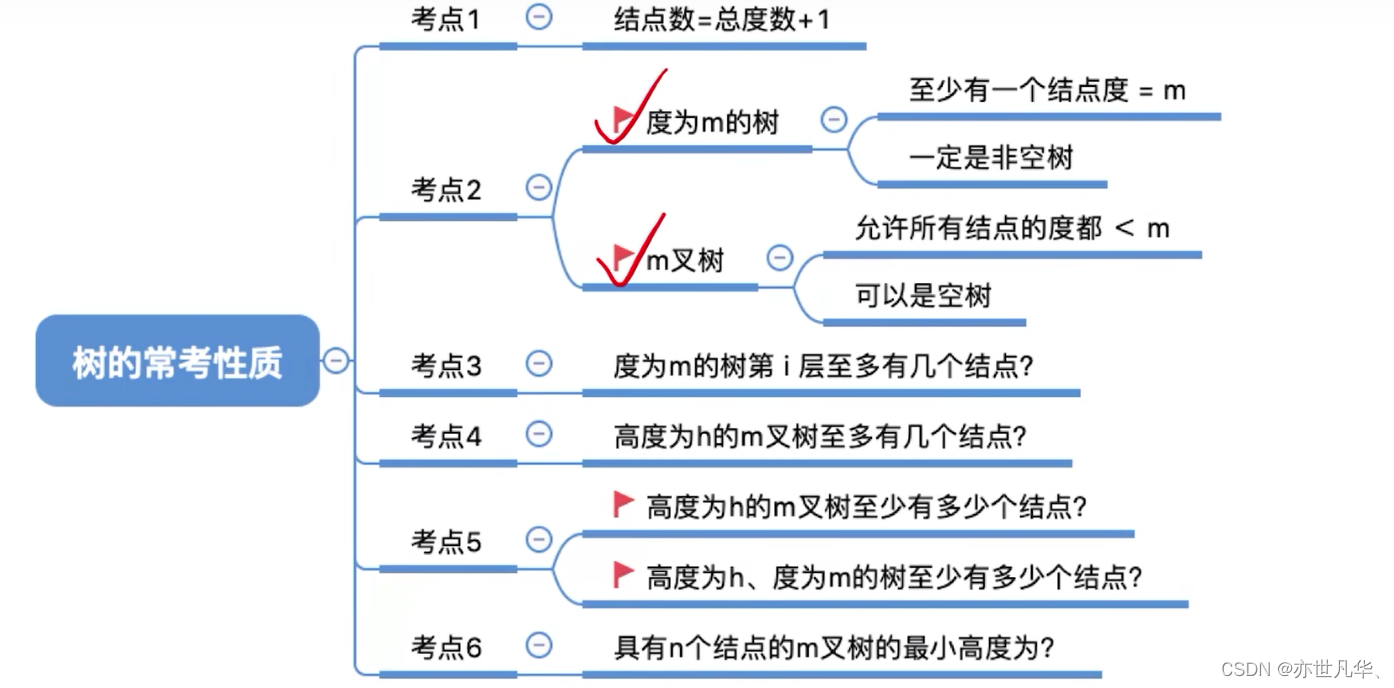
树的常考性质
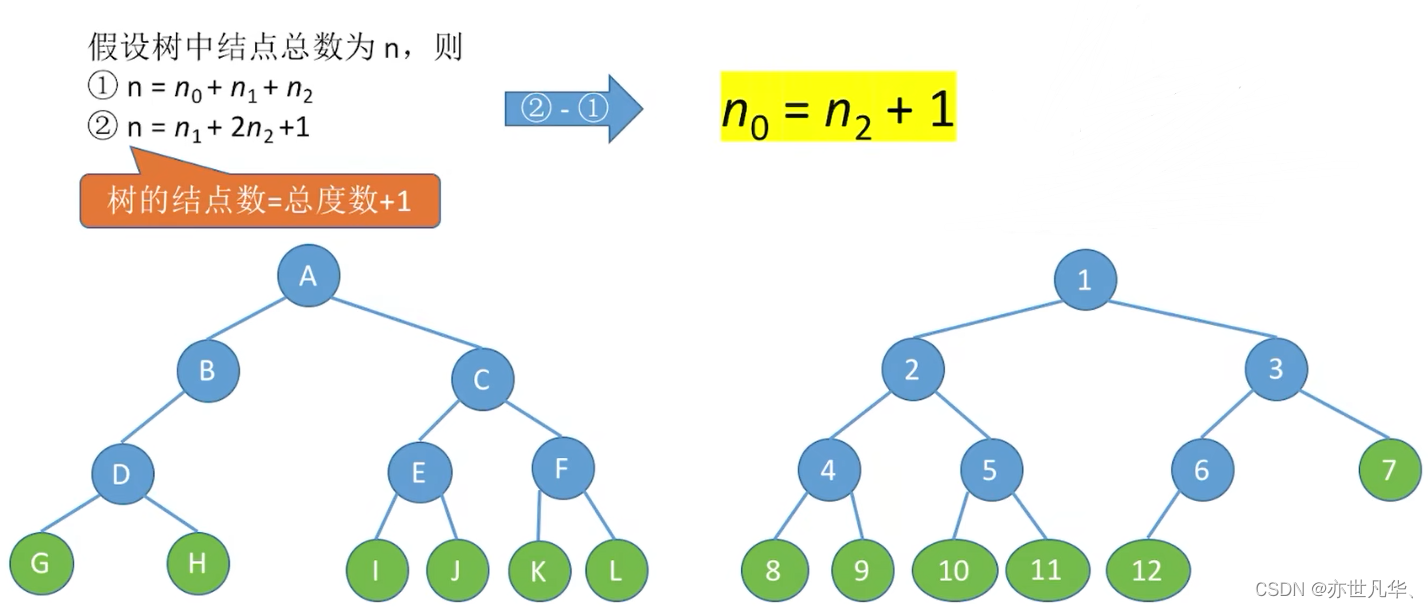
常见考点1:结点数 = 总度数 + 1
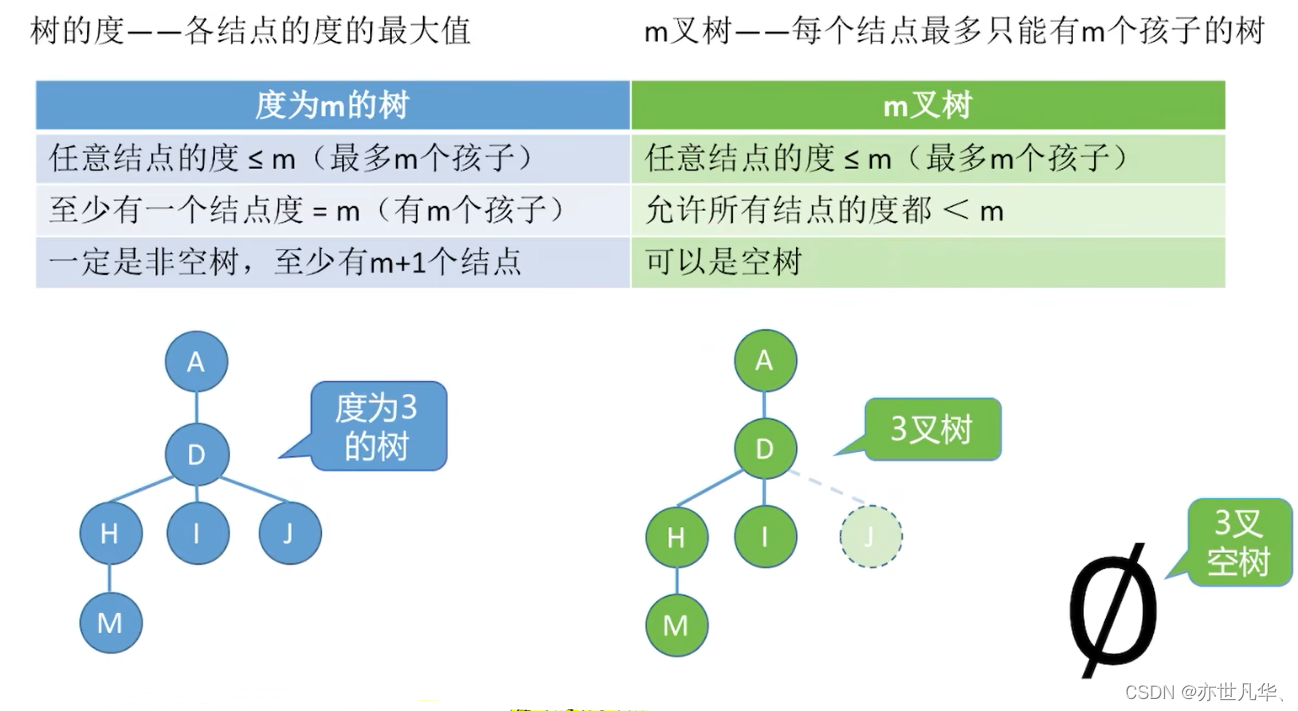
常见考点2:度为m的树、m叉树的区别
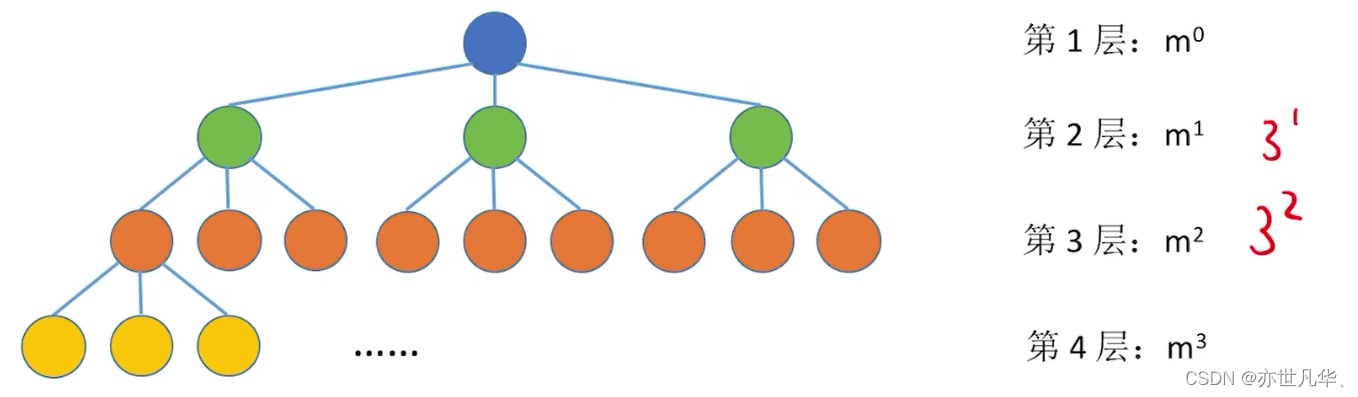
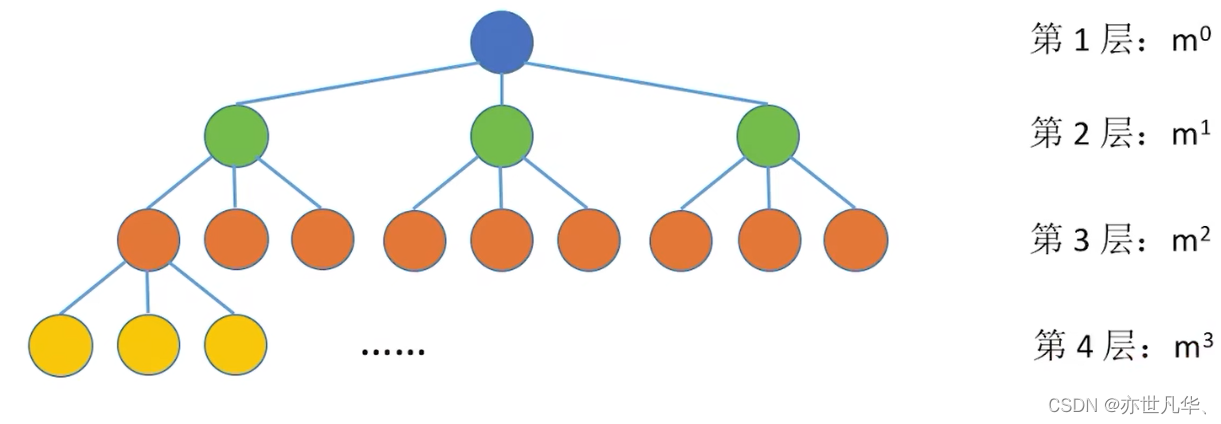
常见考点3:度为m的树第i层至多有
个结点 (i
1),同理m叉树第i层至多有
个结点 (i
1):
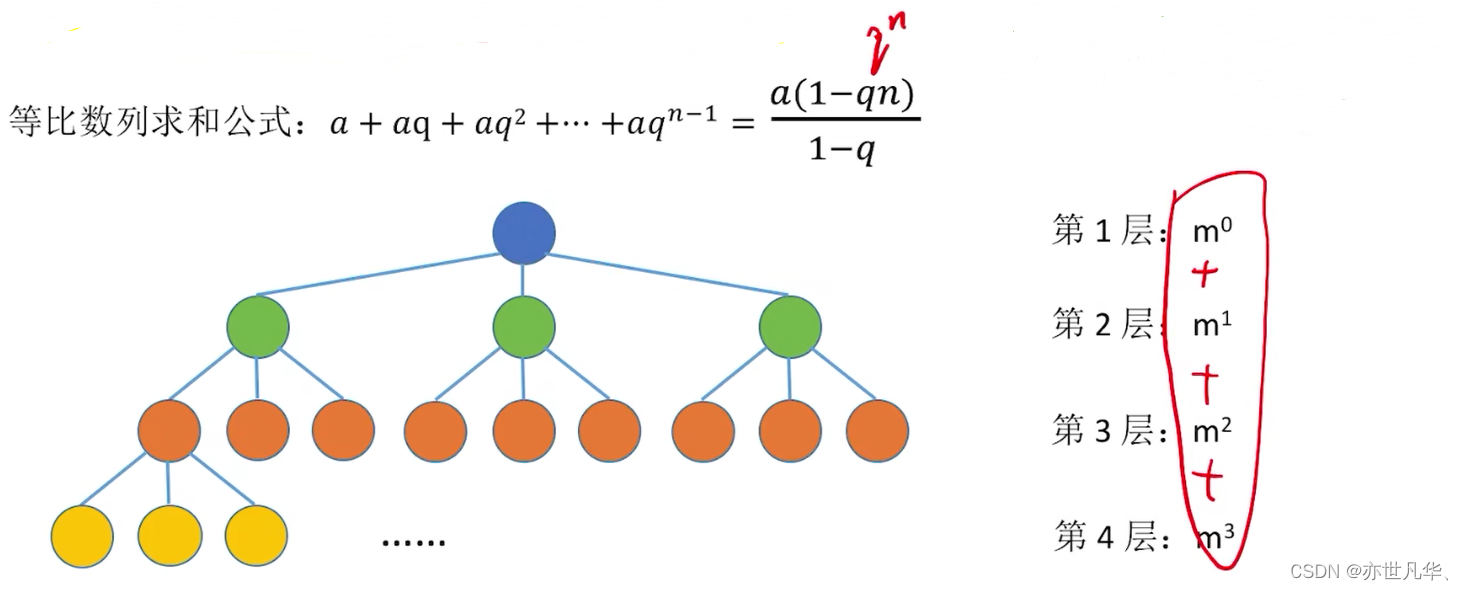
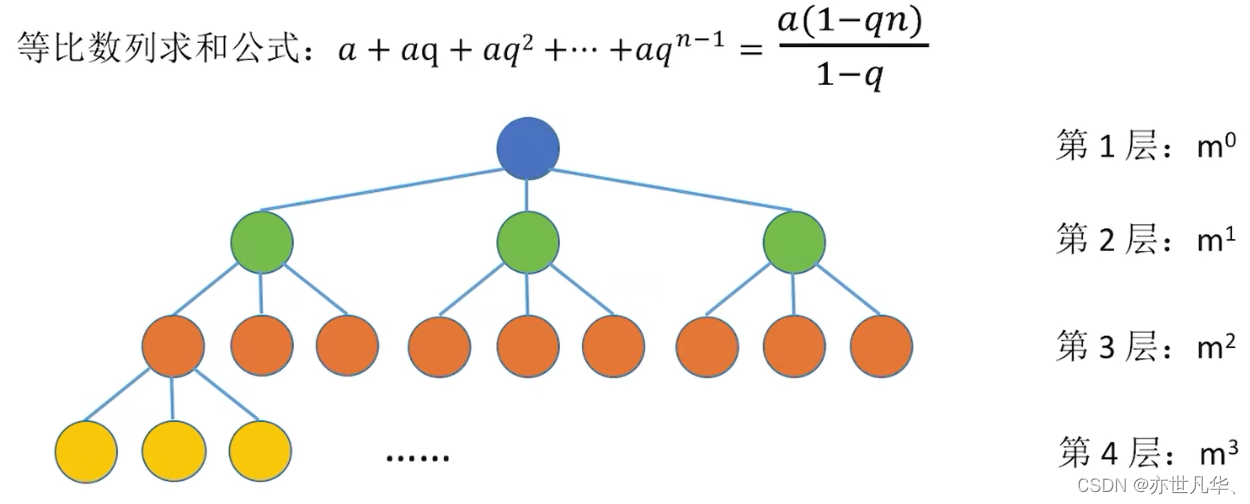
常见考点4:高度为h的m叉树至多有
个结点。
常见考点5:高度为h的m叉树至少有h个结点。高度为h度为m的树至少有h+m-1个结点。
常见考点6:具有n个结点的m叉树的最小高度为
高度最小的情况——所有结点都有m个孩子:
回顾重点,其主要内容整理成如下内容:
二叉树的定义及其性质
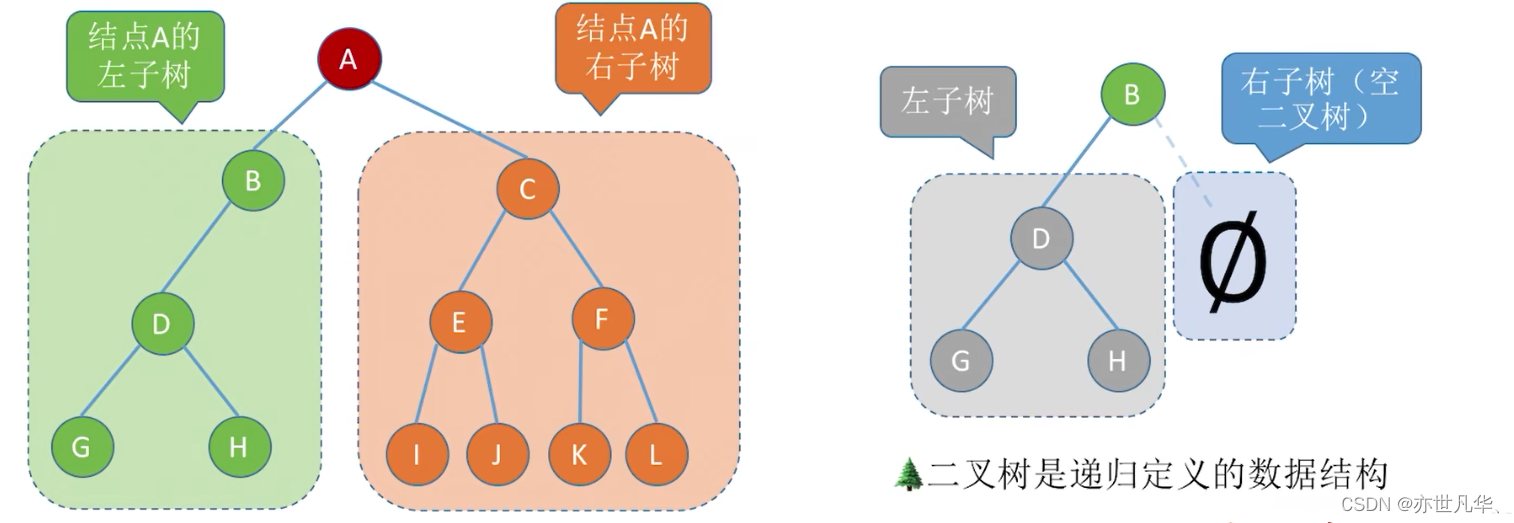
二叉树定义:
二叉树是n(n
0)个结点的有限集合,其有以下两种情况:
1)为空二叉树,即 n = 0 的时候
2)由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一颗二叉树。
特点:每个结点至多只有两颗子树;左右子树不能颠倒。
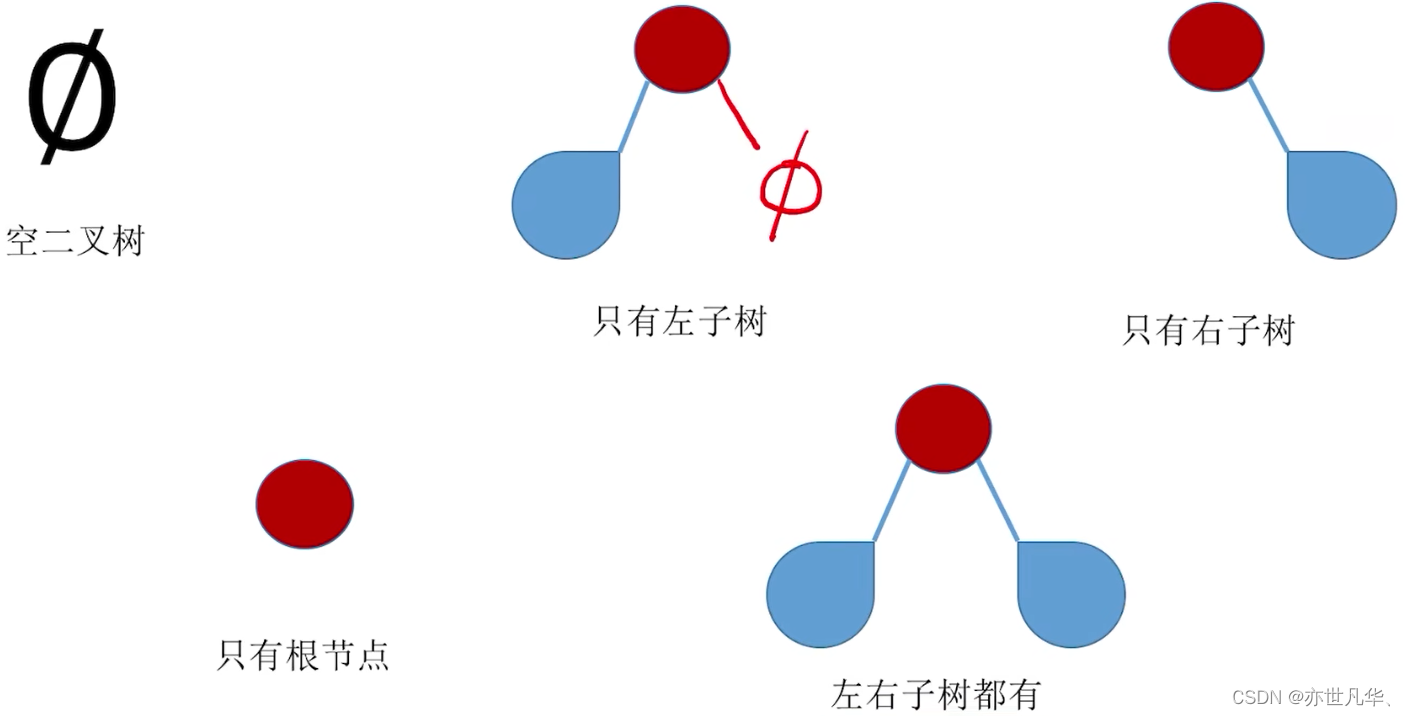
二叉树的五种状态:
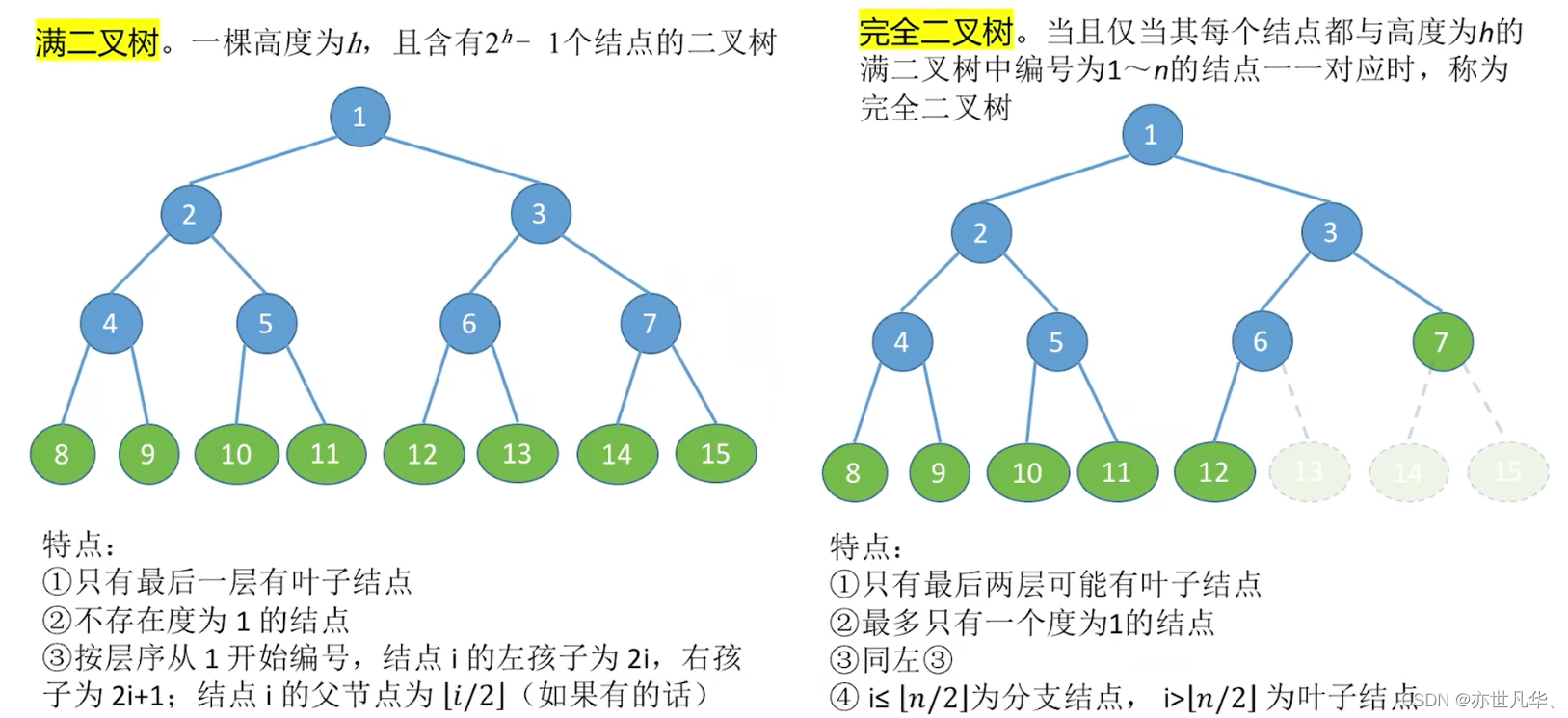
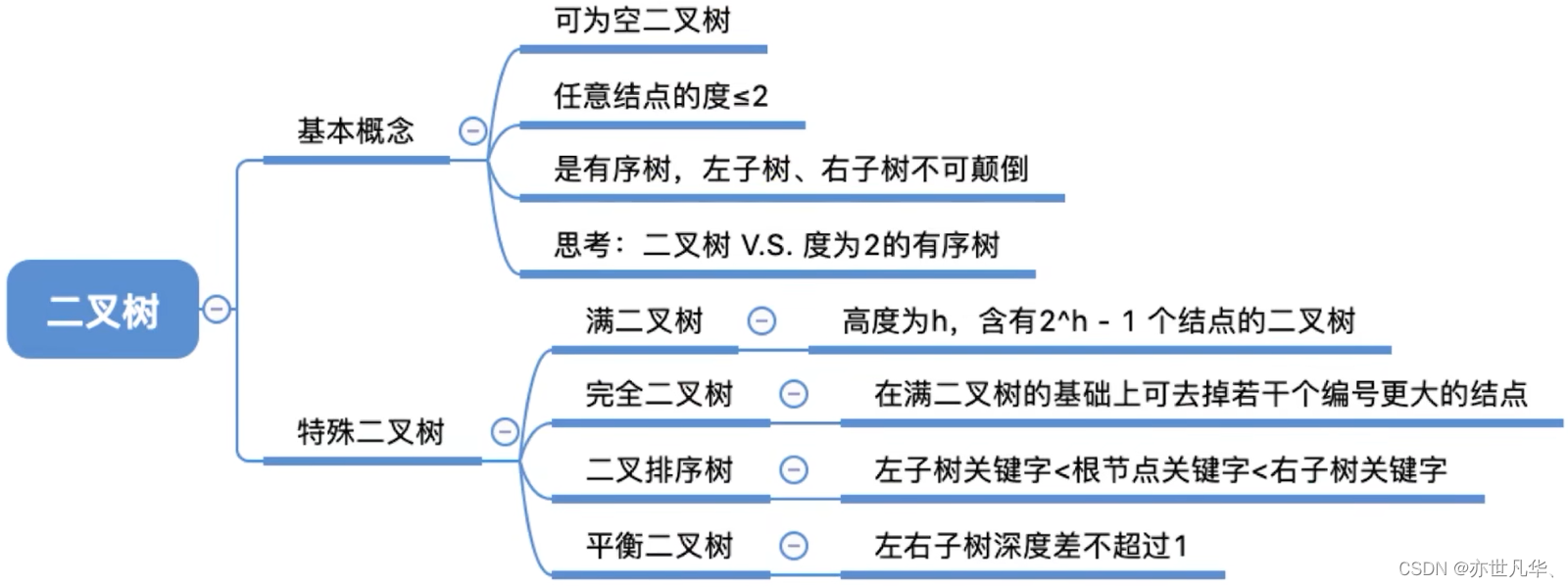
几个特殊的二叉树:
满二叉树:所有叶节点都在同一层,并且所有非叶节点都有两个子节点的二叉树称为满二叉树。
完全二叉树:除了最后一层节点之外,所有节点都拥有两个子节点,并且最后一层的节点都向左对齐的二叉树称为完全二叉树。
二叉排序树:(比如找关键字为60的结点)
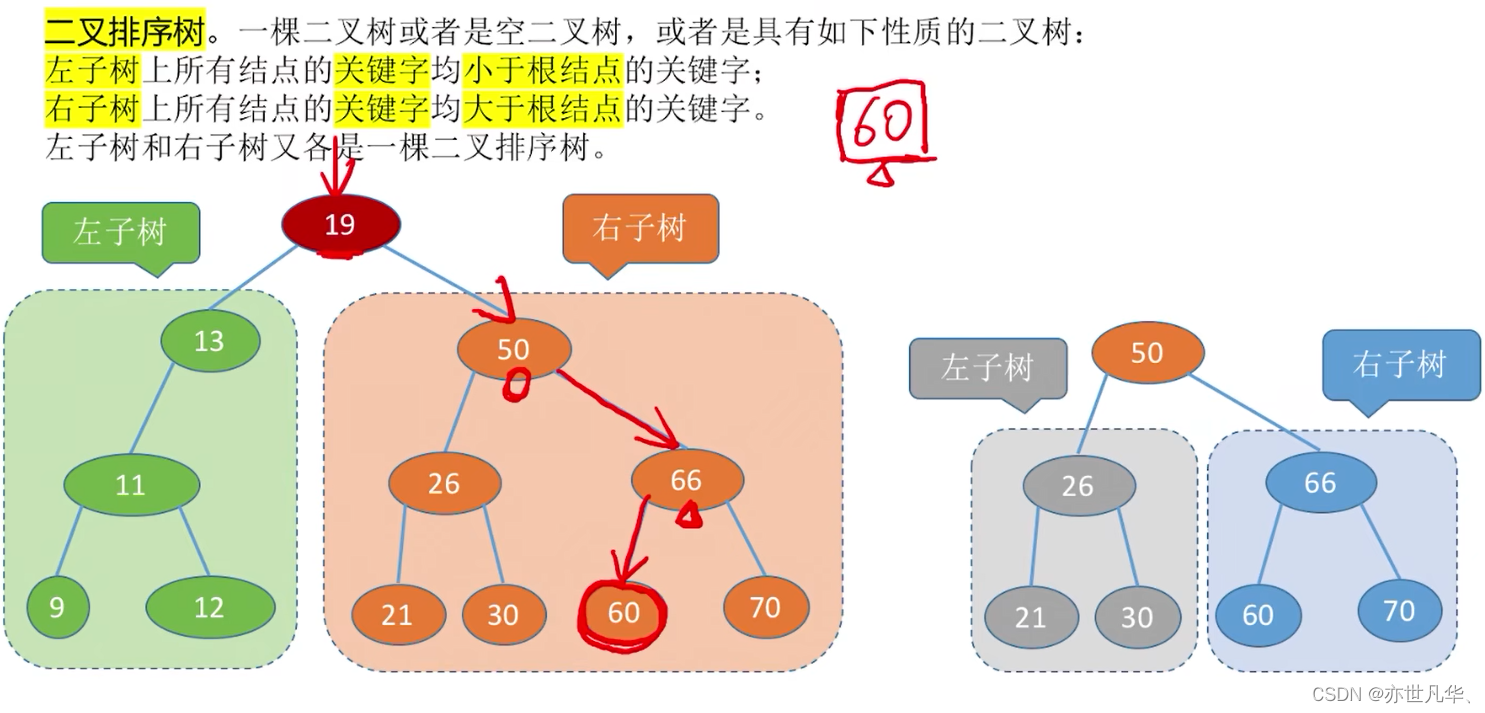
平衡二叉树:树上任一结点的左子树和右子树的深度之差不超过1。
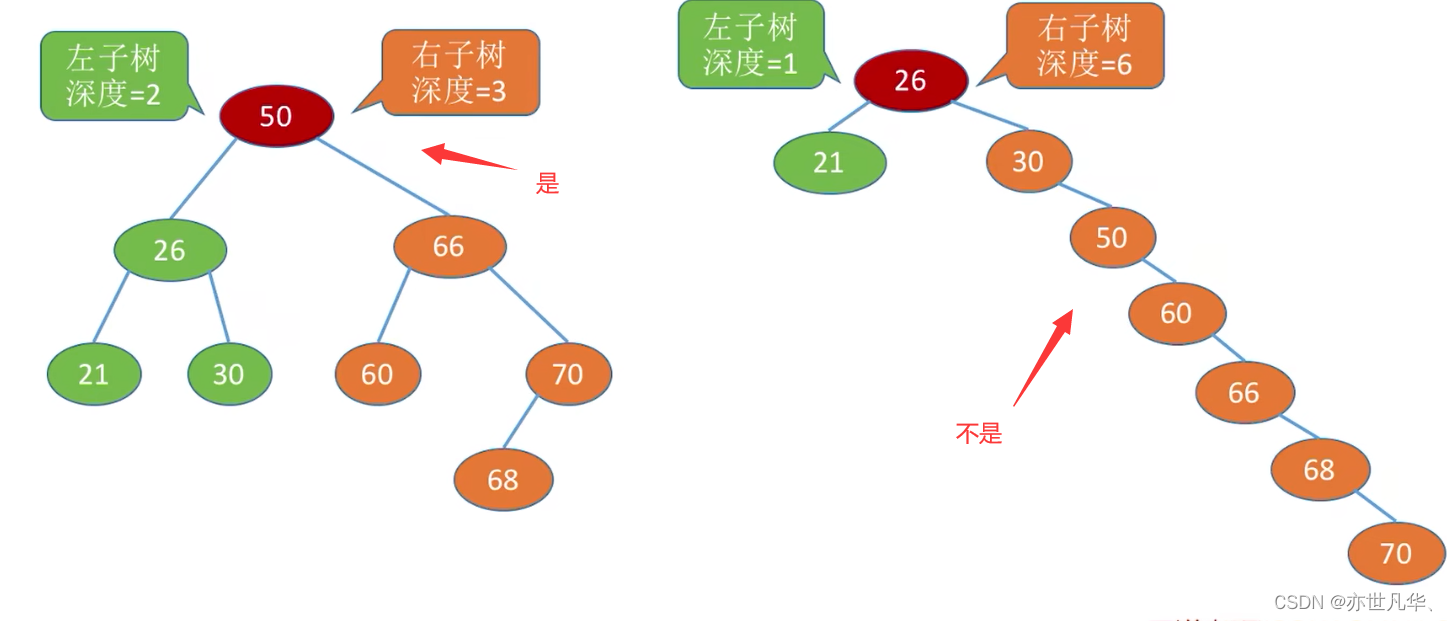
回顾重点,其主要内容整理成如下内容:
二叉树的常考性质:
常见考点1:设非空二叉树中度为0、1和2的结点个数分别为
,则
叶子结点比二分支结点多一个
常见考点2:二叉树第i层至多有
个结点(i
1);m叉树第i层至多有
个结点(i
1)
常见考点3:高度为h的二叉树至多有
个结点(满二叉树)
高度为h的m叉树至多有
个结点
完全二叉树的常考性质:
常见考点1:具有n个(n>0)结点的完全二叉树的高度h为
或
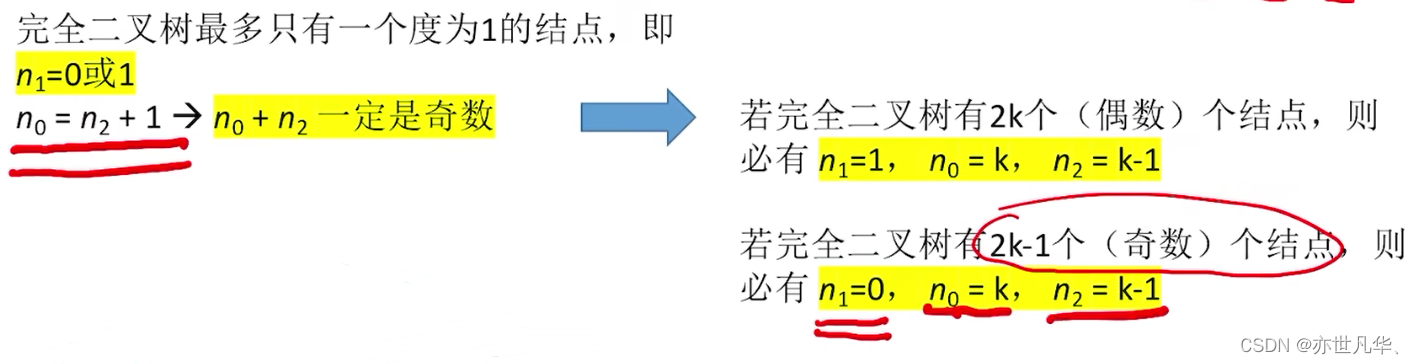
常见考点2:对于完全二叉树,可以由结点数 n 推出度为 0、1和2的结点个数为
、
和
回顾重点,其主要内容整理成如下内容:

二叉树的表示
在数据结构中,二叉树可以通过数组表示和链表存储表示两种方式来实现。下面分别对这两种表示方式进行简述:
数组表示:
数组表示是将二叉树的节点按照某种方式存储在一个一维数组中。一般情况下,数组可以按照层次遍历的顺序存储二叉树的节点。假设根节点存储在数组下标为0的位置,那么对于任意一个节点的索引 i,其左子节点的索引为 2i+1,右子节点的索引为 2i+2。如果某个位置为空,可以使用特定的空值表示。
数组表示的优点:
数组表示的优点是存储简单,通过数组索引可以快速访问到任意节点。缺点是当二叉树的形状发生改变时,需要重新调整数组的大小,可能涉及到大量的元素移动。
#include <stdio.h>
#include <stdlib.h>// 二叉树节点结构体
struct TreeNode {int val;struct TreeNode* left;struct TreeNode* right;
};// 构建二叉树的数组表示
struct TreeNode* build_binary_tree(int arr[], int size) {struct TreeNode** tree = malloc(sizeof(struct TreeNode*) * size);for (int i = 0; i < size; i++) {if (arr[i] != -1) {struct TreeNode* node = malloc(sizeof(struct TreeNode));node->val = arr[i];node->left = NULL;node->right = NULL;tree[i] = node;} else {tree[i] = NULL;}}for (int i = 0; i < size; i++) {if (tree[i] != NULL) {if (2 * i + 1 < size)tree[i]->left = tree[2 * i + 1];if (2 * i + 2 < size)tree[i]->right = tree[2 * i + 2];}}struct TreeNode* root = tree[0];free(tree);return root;
}// 测试代码
int main() {int arr[] = {1, 2, 3, 4, 5, 6, 7};int size = sizeof(arr) / sizeof(arr[0]);struct TreeNode* root = build_binary_tree(arr, size);// 输出测试结果printf("root: %d\n", root->val);printf("left child of root: %d\n", root->left->val);printf("right child of root: %d\n", root->right->val);return 0;
}链表存储表示:
链表存储表示是使用链表的方式来表示二叉树。每个节点包含一个指向其父节点的指针,一个指向其左子节点的指针,一个指向其右子节点的指针。
链表存储表示的优点:
链表存储表示的优点是可以灵活地插入、删除节点而不需要移动其他节点,适用于频繁变化的二叉树结构。缺点是访问某个节点需要从根节点开始遍历,效率相对较低。
#include <stdio.h>
#include <stdlib.h>// 二叉树节点结构体
struct TreeNode {int val;struct TreeNode* left;struct TreeNode* right;
};// 构建二叉树的链表存储表示
struct TreeNode* build_binary_tree(int arr[], int size) {if (size == 0) {return NULL;}struct TreeNode* root = malloc(sizeof(struct TreeNode));root->val = arr[0];root->left = NULL;root->right = NULL;struct TreeNode** queue = malloc(sizeof(struct TreeNode*) * size);int front = 0;int rear = 0;queue[rear++] = root;int i = 1;while (i < size) {struct TreeNode* node = queue[front++];// 处理左子节点if (arr[i] != -1) {node->left = malloc(sizeof(struct TreeNode));node->left->val = arr[i];node->left->left = NULL;node->left->right = NULL;queue[rear++] = node->left;}i++;// 处理右子节点if (i < size && arr[i] != -1) {node->right = malloc(sizeof(struct TreeNode));node->right->val = arr[i];node->right->left = NULL;node->right->right = NULL;queue[rear++] = node->right;}i++;}free(queue);return root;
}// 测试代码
int main() {int arr[] = {1, 2, 3, 4, 5, 6, 7};int size = sizeof(arr) / sizeof(arr[0]);struct TreeNode* root = build_binary_tree(arr, size);// 输出测试结果printf("root: %d\n", root->val);printf("left child of root: %d\n", root->left->val);printf("right child of root: %d\n", root->right->val);return 0;
}二叉树遍历
遍历:按照某种次序把所有结点都访问一遍。根据二叉树的递归特性要么是个空二叉树,要么就是由“根结点+左子树+右子树”组成的二叉树
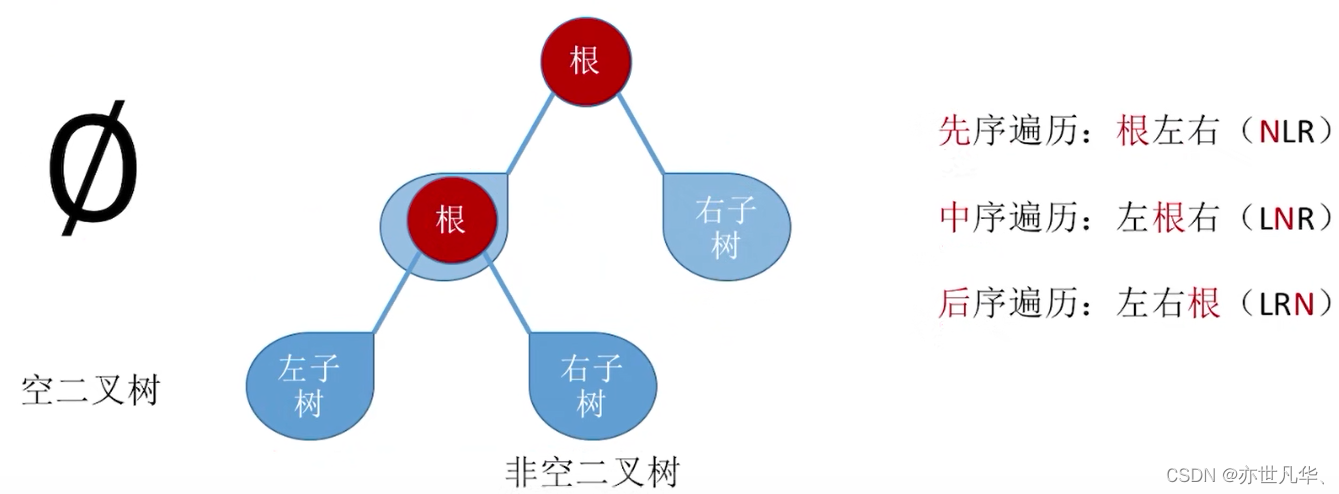
根据二叉树的三种遍历规则,相关的具体案例如下:
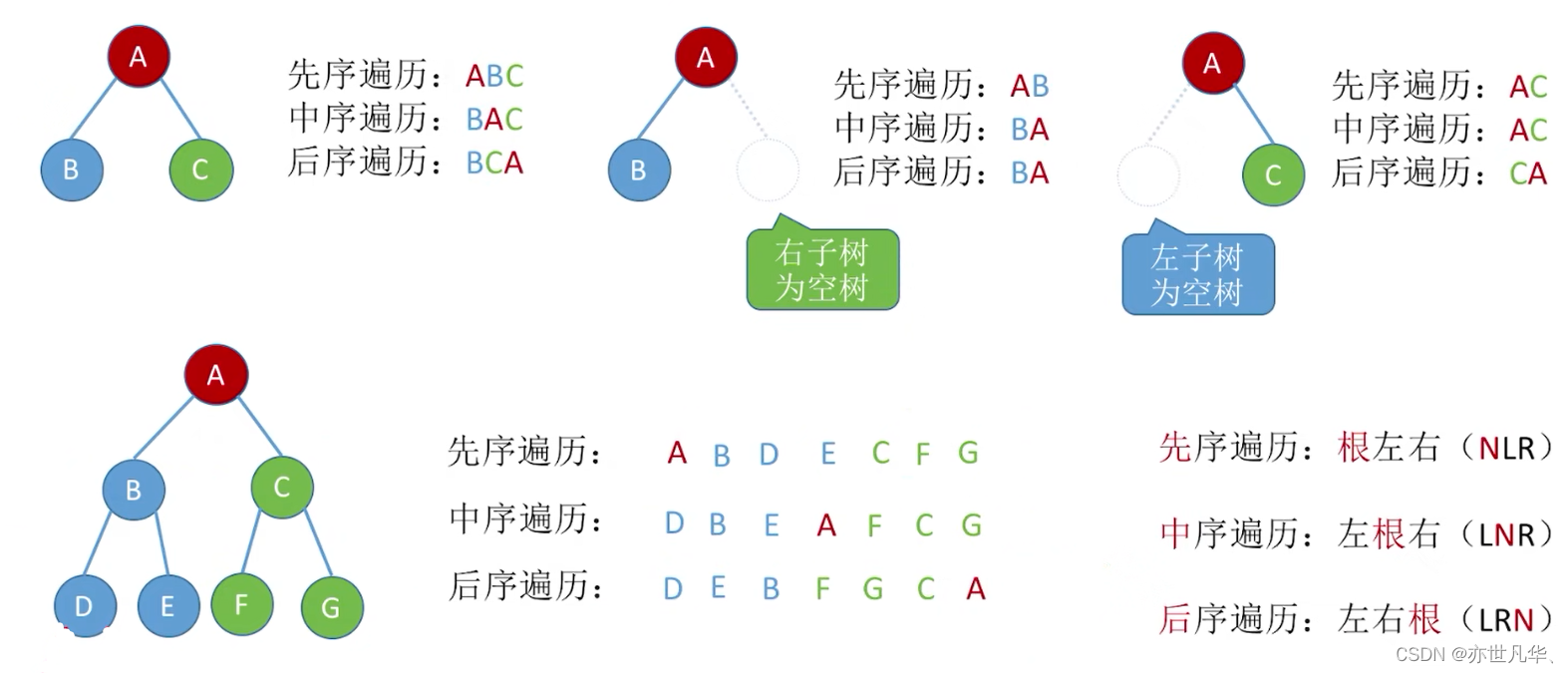
再进行具体的练习一遍:

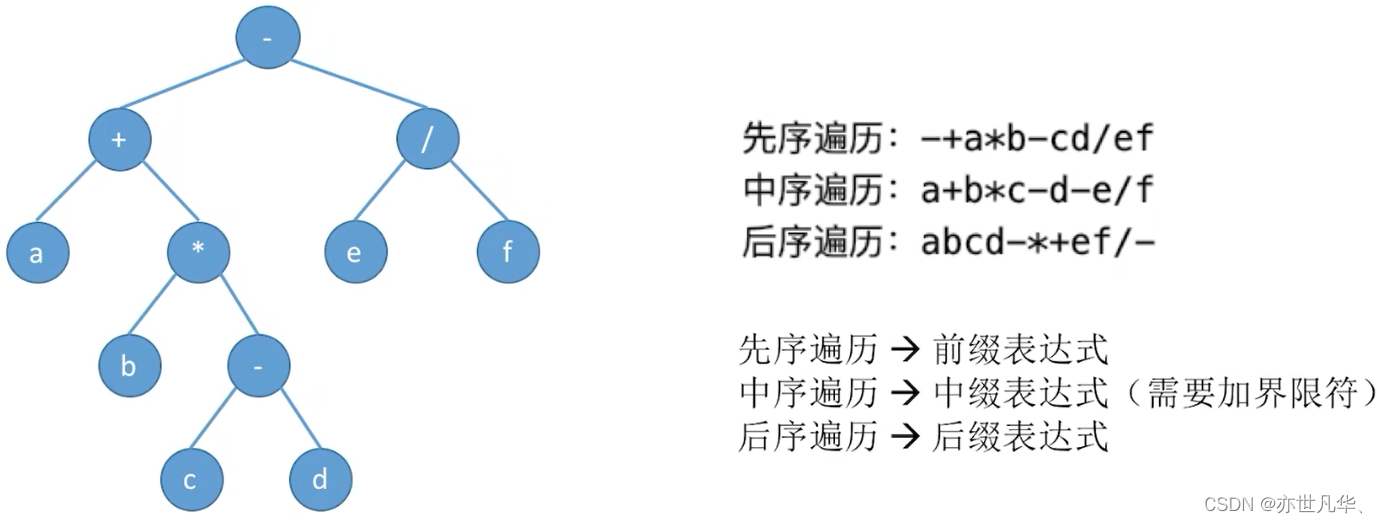
回顾重点,其主要内容整理成如下内容:
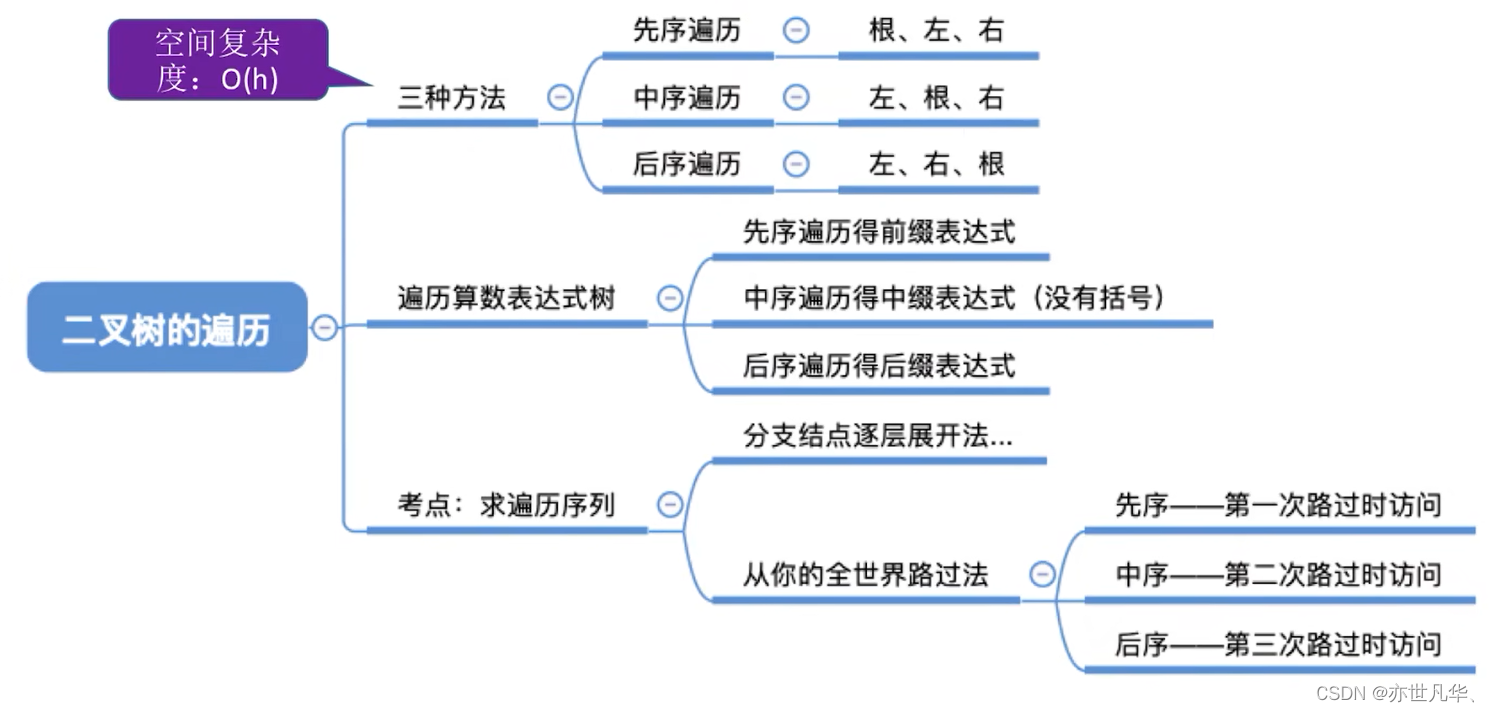
二叉树的层序(次)遍历:
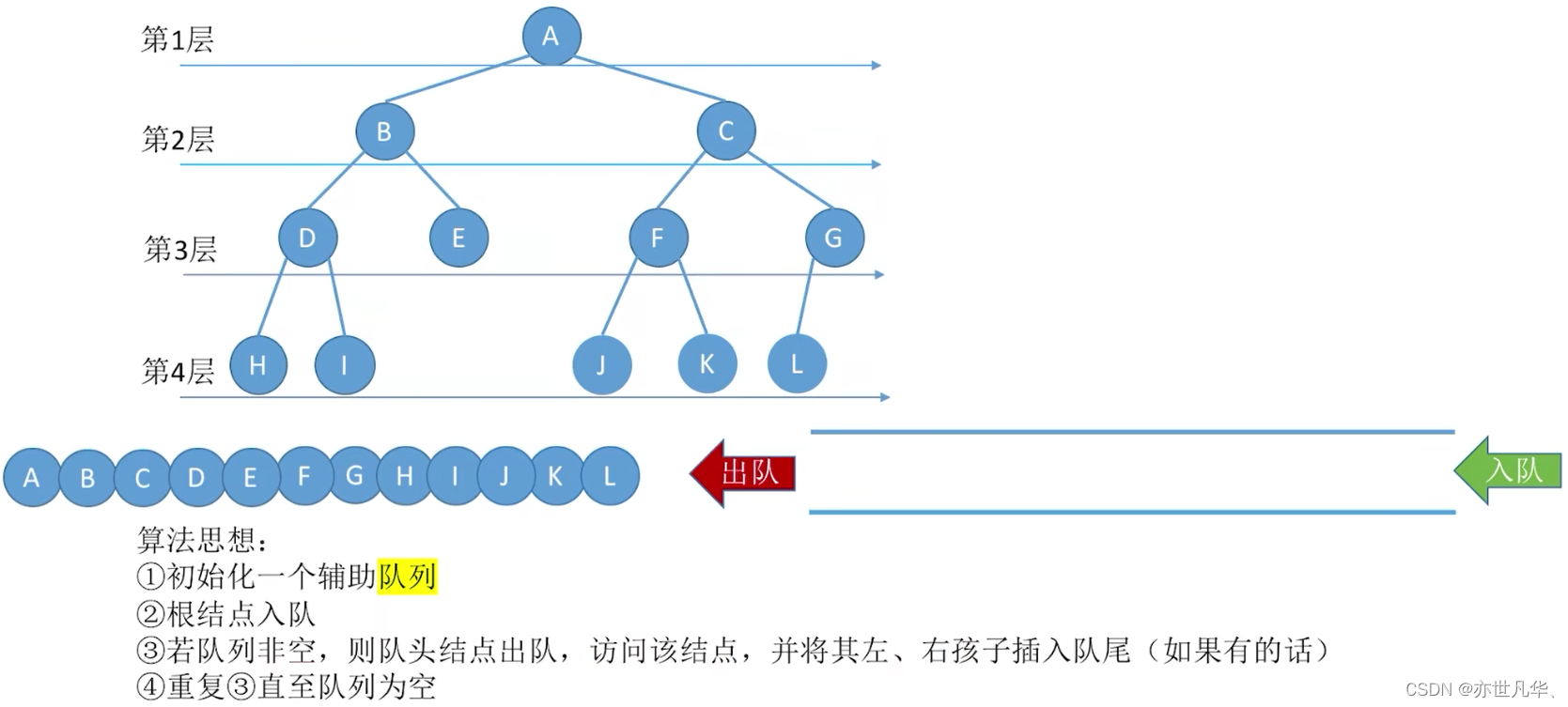
其相应的代码实现如下:

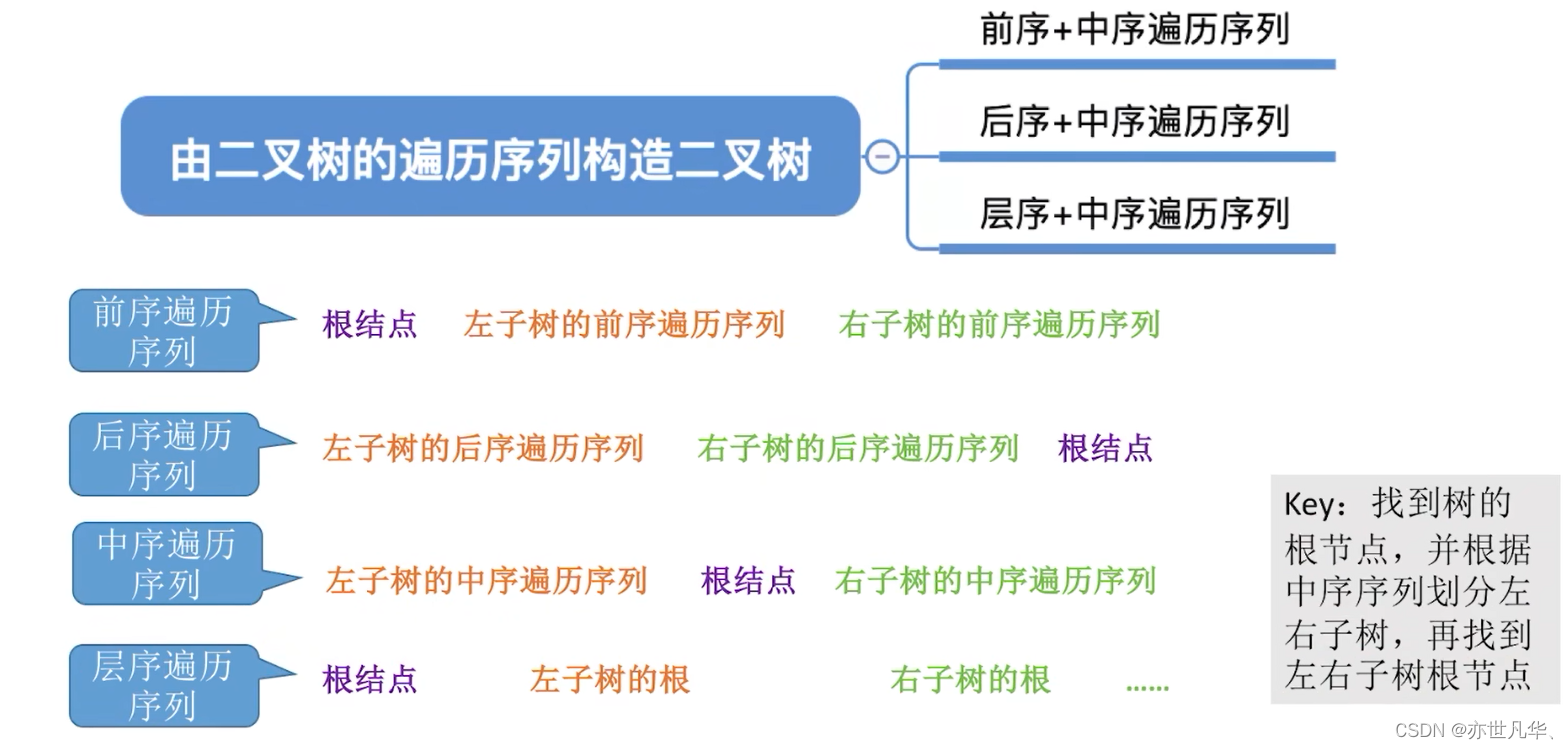
由遍历序列构造二叉树:
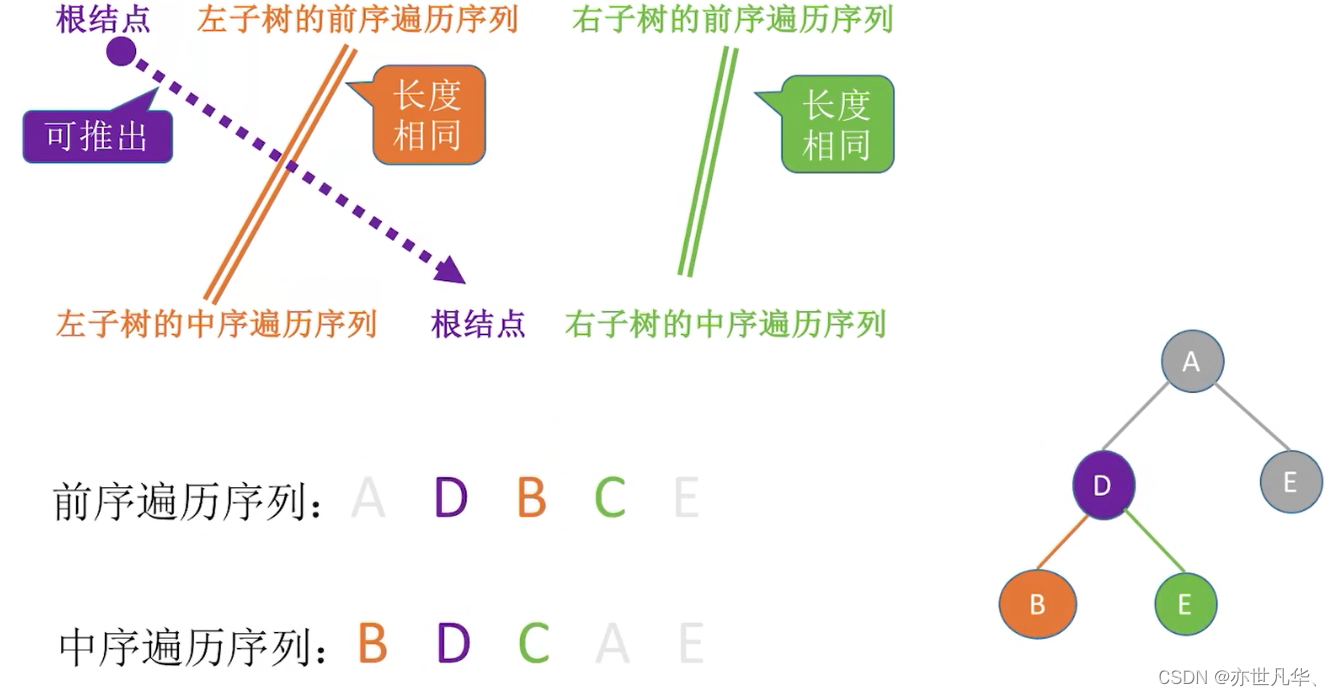
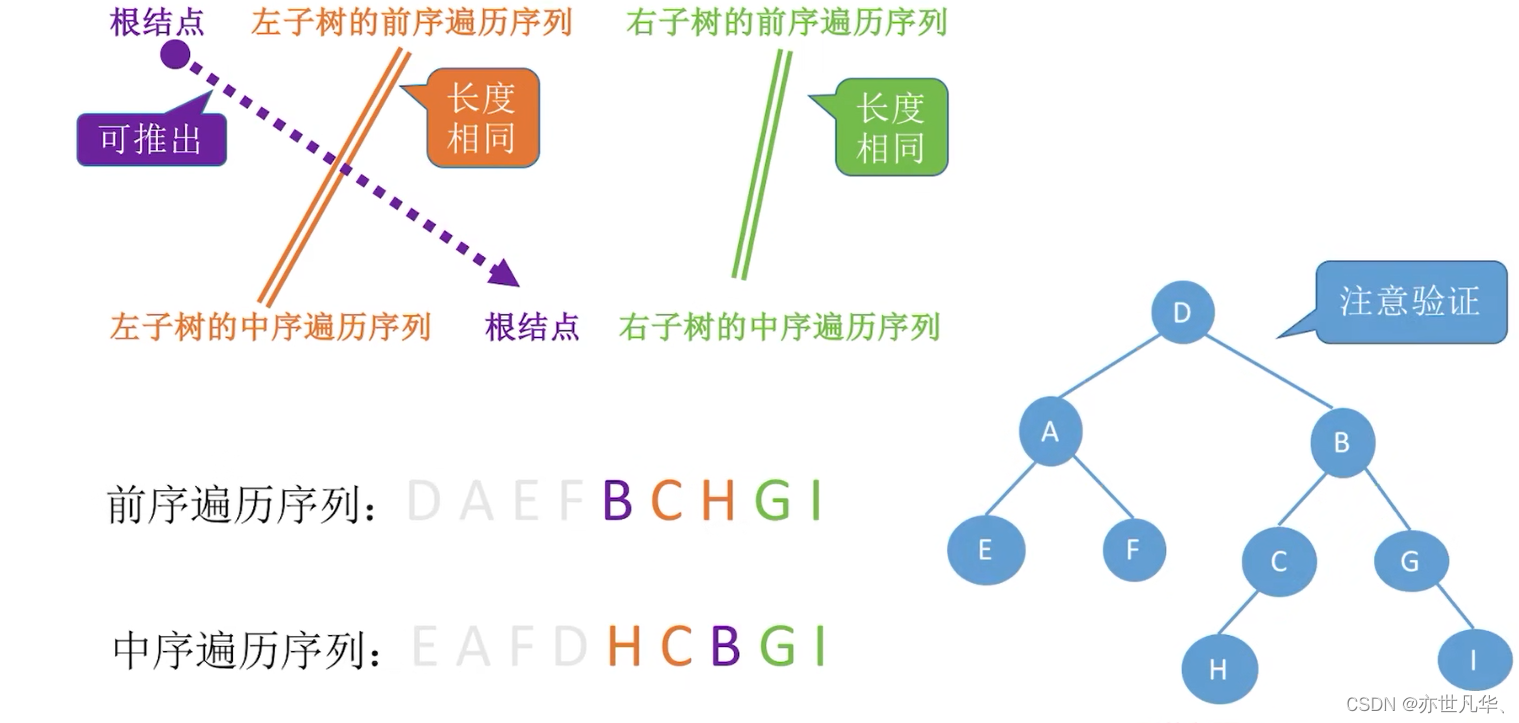
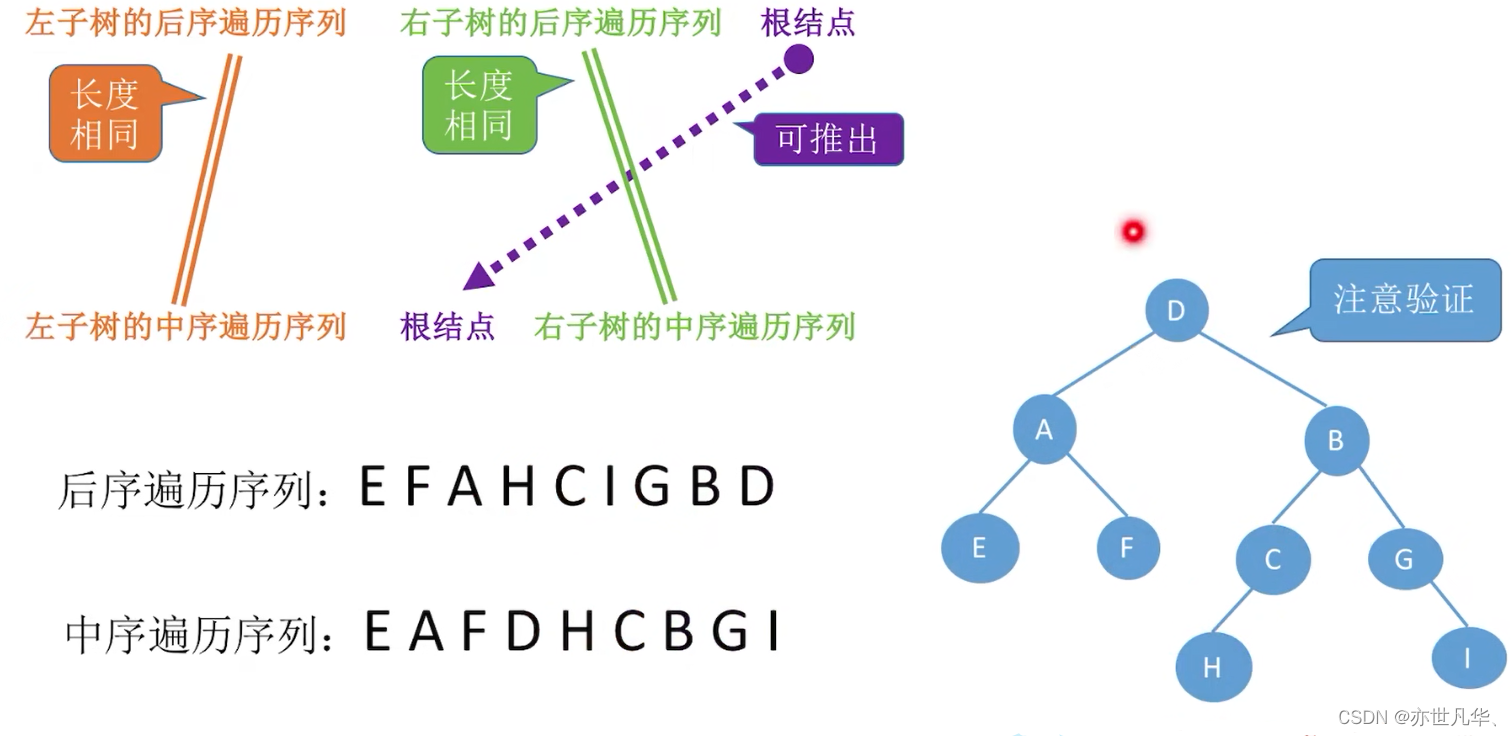
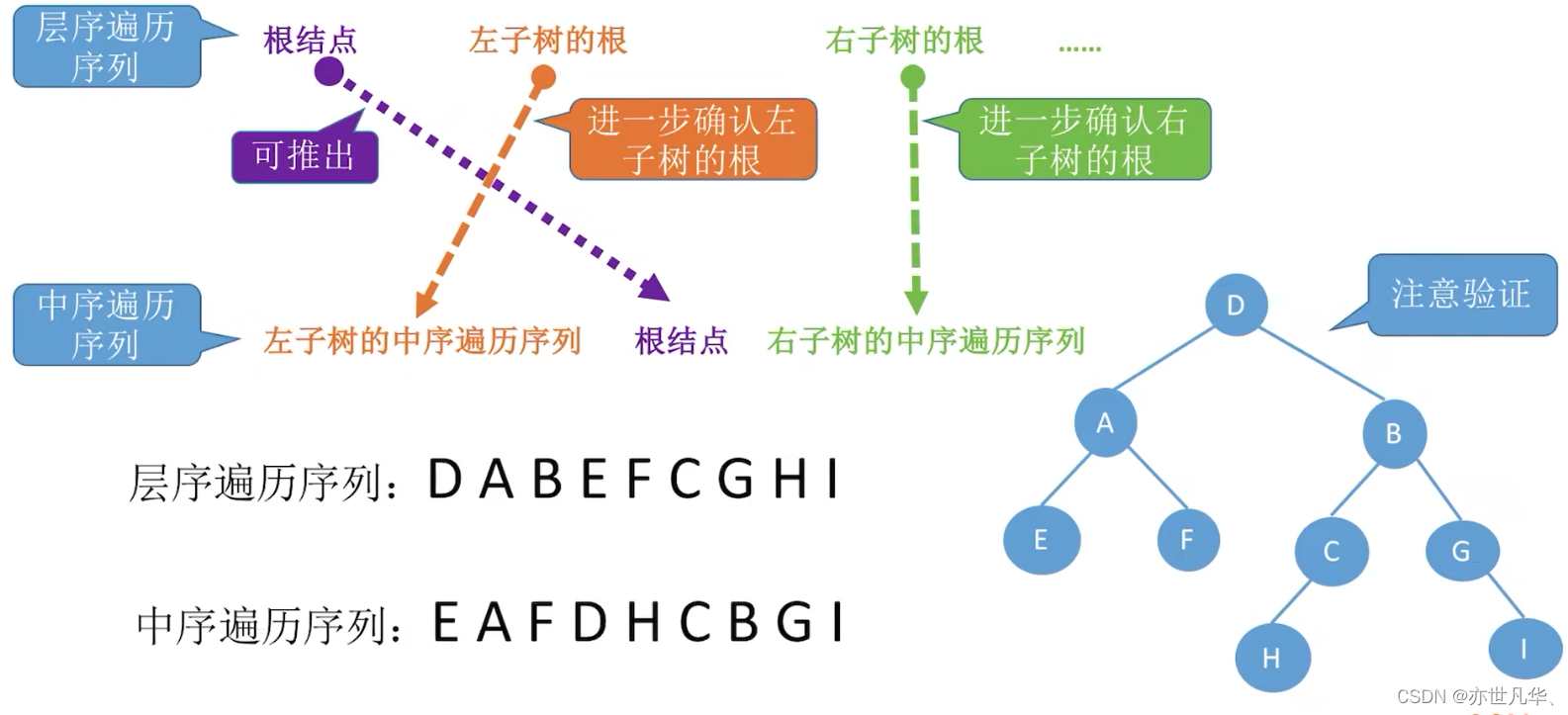

回顾重点,其主要内容整理成如下内容:
相关文章:

数据结构--》解锁数据结构中树与二叉树的奥秘(一)
数据结构中的树与二叉树,是在建立非线性数据结构方面极为重要的两个概念。它们不仅能够模拟出生活中各种实际问题的复杂关系,还常被用于实现搜索、排序、查找等算法,甚至成为一些大型软件和系统中的基础设施。 无论你是初学者还是进阶者&…...
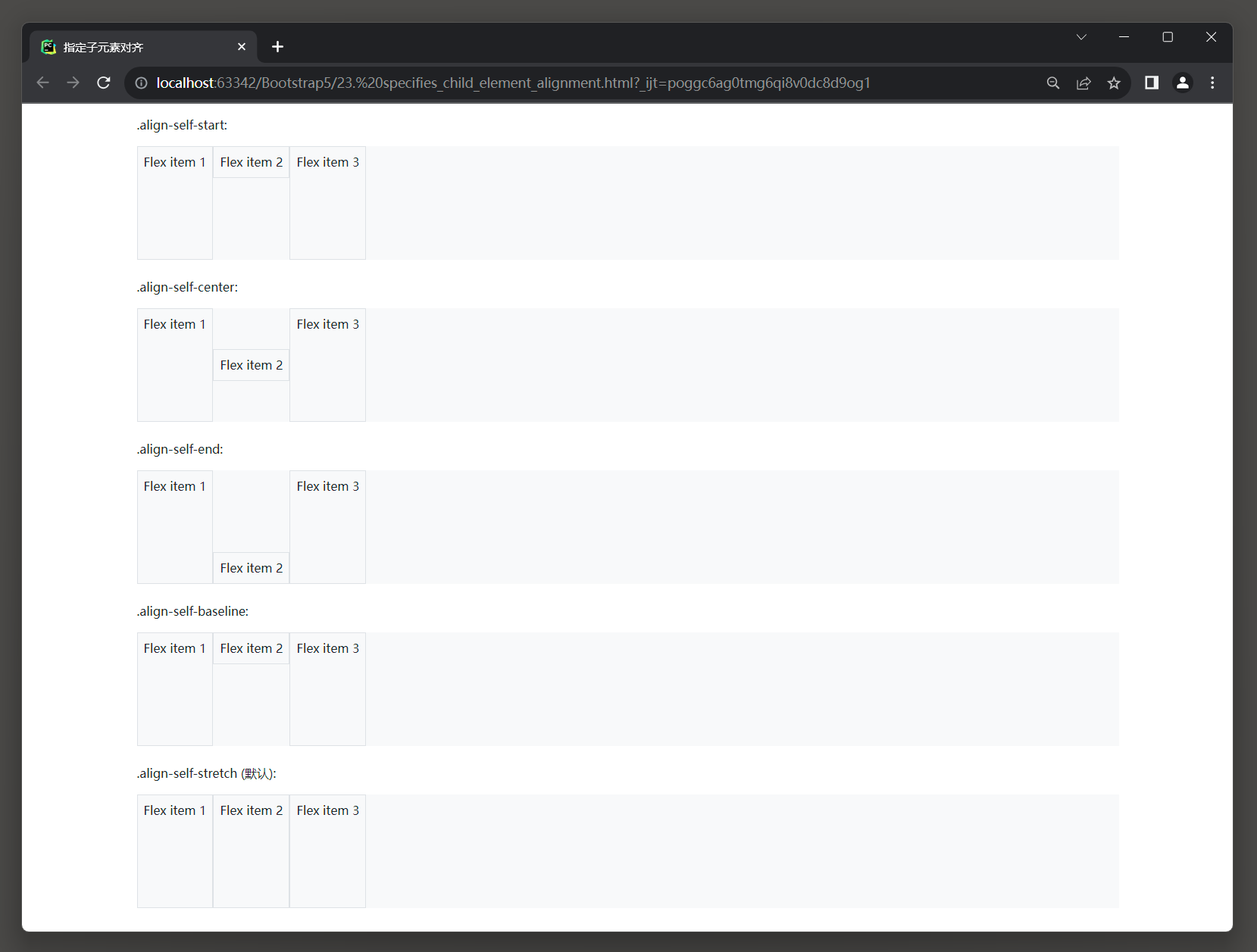
23.4 Bootstrap 框架5
1. 背景颜色 1.1 背景颜色样式 在Bootstrap 5中, 可以使用以下类来设置背景颜色: * 1. .bg-primary: 设置为主要的背景颜色(#007bff, 深蓝色). * 2. .bg-secondary: 设置为次要的背景颜色(#6c757d, 灰色). * 3. .bg-success: 设置为成功的背景颜色(#28a745, 绿色). * 4. …...
Spring源码解析——IOC属性填充
正文 doCreateBean() 主要用于完成 bean 的创建和初始化工作,我们可以将其分为四个过程: 最全面的Java面试网站 createBeanInstance() 实例化 beanpopulateBean() 属性填充循环依赖的处理initializeBean() 初始化 bean 第一个过程实例化 bean在前面一篇…...

寒露到了,冬天还会远吗?
寒露惊秋晚,朝看菊渐黄。 日复一日间,光影如梭,我们便很快将告别了秋高气爽,白日将变得幽晦, 天寒夜长,风气萧索,雾结烟愁。 还没好好体会秋高气爽,寒露就到了。 今天晚上9点多,我们…...

科普②| 大数据有什么用?大数据技术的应用领域有哪些?
1、提供个性服务很多人觉得大数据好像离我们很远,其实我们在日常所使用的智能设备,就需要大数据的帮助。比如说我们运动时候戴的运动手表或者是运动手环,就可以在我们平时运动的时候,帮助我们采集运动数据及热量消耗情况。进入睡眠…...

golang的切片使用总结二
如果没看golang切片的第一篇总结博客 golang的切片使用总结一-CSDN博客 ,请浏览之 举例9:make([]int, a, b)后访问下标a的元素 s : make([]int, 10, 12) v : s[10] fmt.Printf("v:%v", v) 打印结果: panic: runtime error: index …...
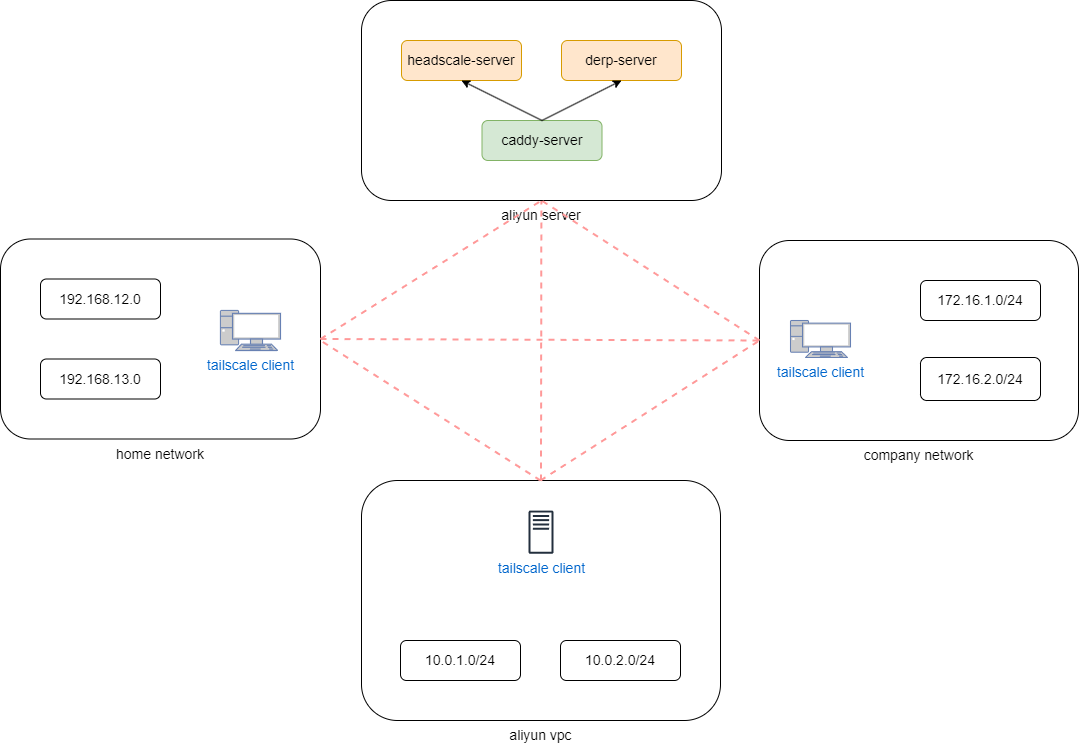
tailscale自建headscale和derp中继
tailscale derp中继服务简介 tailscale是一个基于WireGuard的零配置软件,它可以轻松地在多台设备之间建立点对点加密连接。 derp服务器是tailscale网络的重要组成部分。它作为tailscale客户端之间的中继,帮助客户端找到并连接到其他客户端设备。 但Tailscale 官方…...
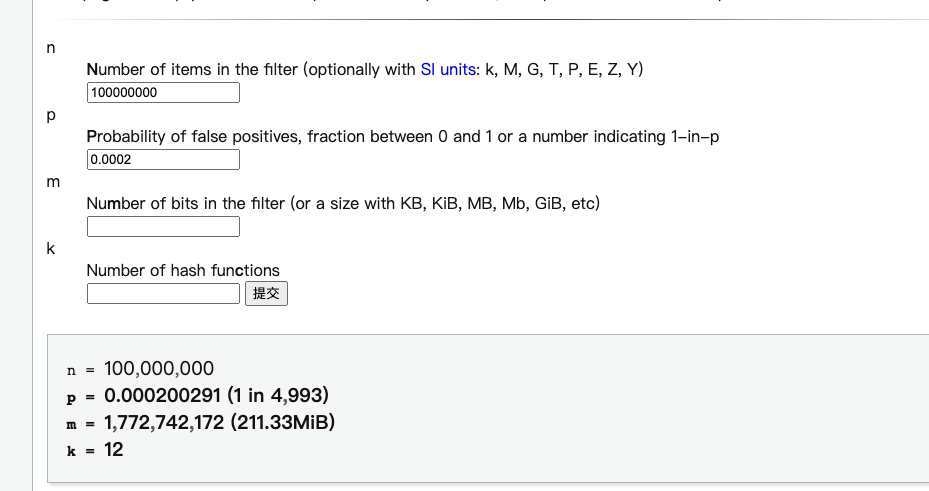
布隆过滤器的使用
布隆过滤器简介 Bloom Filter(布隆过滤器)是一种多哈希函数映射的快速查找算法。它是一种空间高效的概率型数据结构,通常应用在一些需要快速判断某个元素是否属于集合,但是并不严格要求100%正确的场合。 布隆过滤器的优势在于,利用很少的空…...

Web开发-单例模式
目录 单例模式介绍代码实现单例模式 单例模式介绍 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点。单例模式可以通过private属性实现。通过将类的构造函数设为private,可以防止类在外部被实例化。单例模式通…...
MySQL:温备份和恢复-mysqldump (4)
介绍 温备:同样是在数据库运行的时候进行备份的,但对当前数据库的操作会产生影响。(只可以读操作,不可以写操作) 温备份的优点: 1.可在表空间或数据文件级备份,备份时间短。 2.备份时数据库依然…...
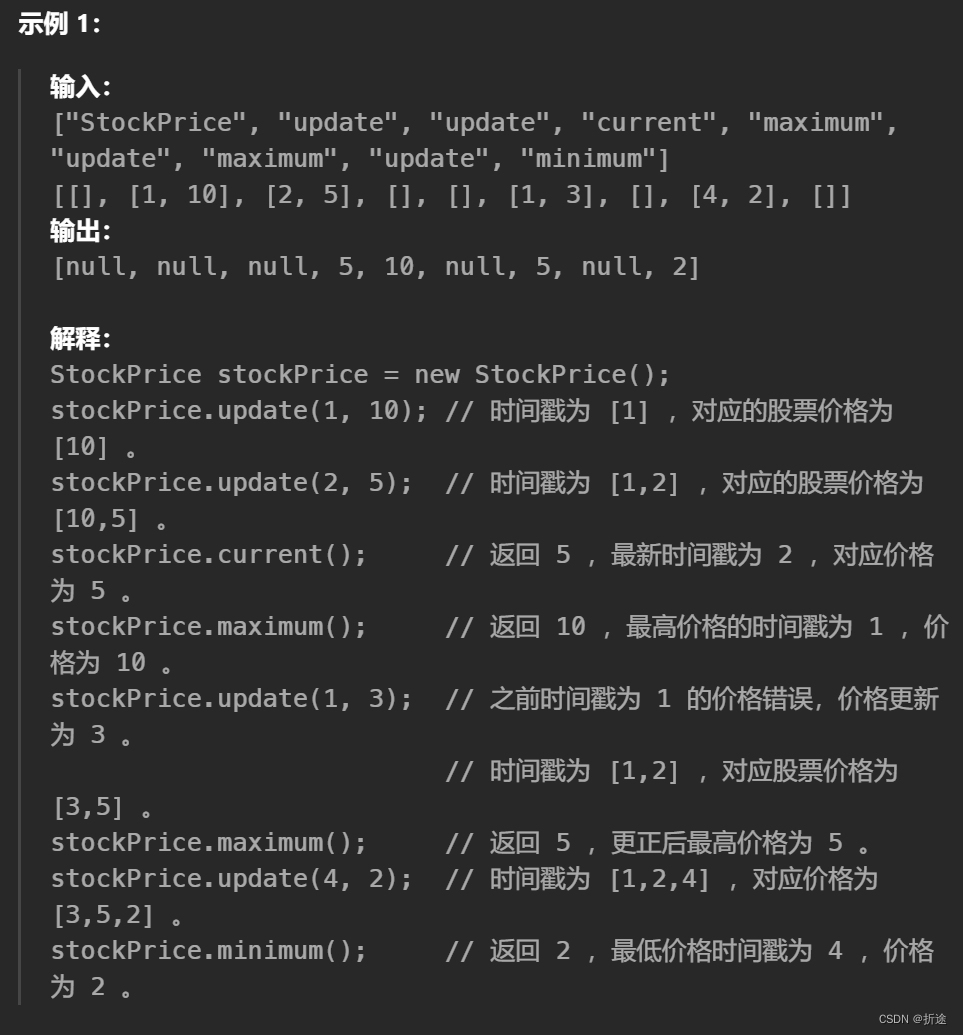
【力扣每日一题】2023.10.8 股票价格波动
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题是程序设计题,要我们实现一个类,一共是四个功能,第一个是给一个时间戳和价格,表示该…...

Linux隐藏文件或文件夹
在Linux中,以点(.)开头的文件或文件夹是隐藏文件或隐藏文件夹。要创建一个隐藏文件或文件夹,可以使用以下命令: 创建隐藏文件: touch .filename这将在当前目录下创建一个名为 “.filename” 的隐藏文件。…...
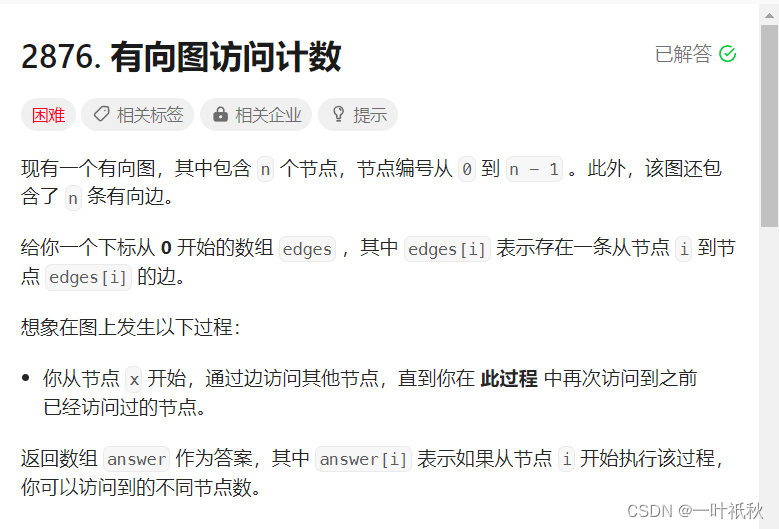
leetcode - 365周赛
一,2873.有序三元组中的最大值 I 该题的数据范围小,直接遍历: class Solution {public long maximumTripletValue(int[] nums) {int n nums.length;long ans 0;for(int i0; i<n-2; i){for(int ji1; j<n-1; j){for(int kj1; k<…...

为什么mac上有的软件删除不掉?
对于Mac用户来说,软件卸载通常是一个相对简单的过程。然而,有时你可能会发现某些软件似乎“顽固不化”,即使按照常规方式尝试卸载,也依然存在于你的电脑上。这到底是为什么呢?本文将探讨这一问题的可能原因。 1.卸载失…...
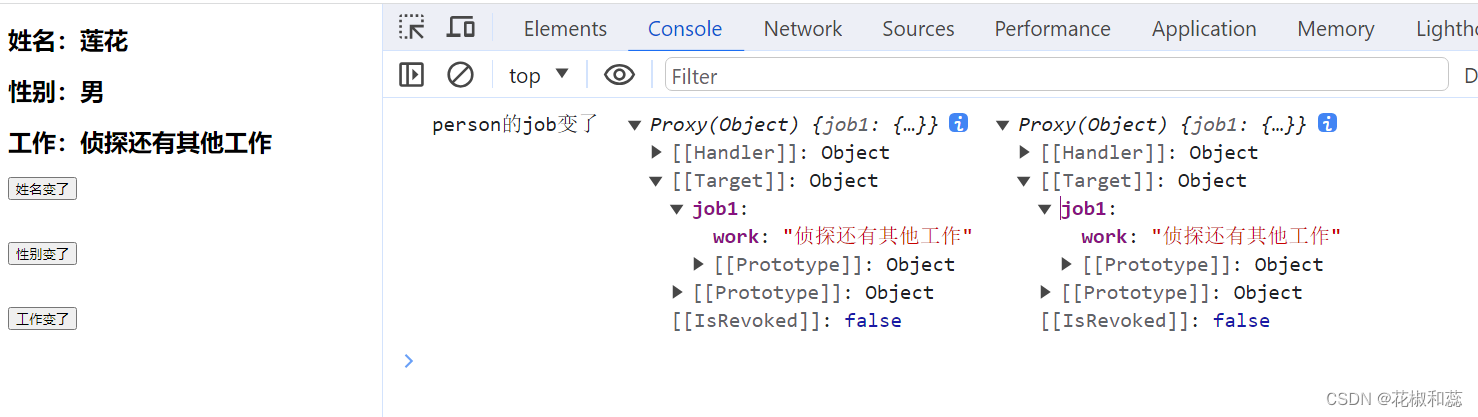
【vue3】wacth监听,监听ref定义的数据,监听reactive定义的数据,详解踩坑点
假期第二篇,对于基础的知识点,我感觉自己还是很薄弱的。 趁着假期,再去复习一遍 之前已经记录了一篇【vue3基础知识点-computed和watch】 今天在学习的过程中发现,之前记录的这一篇果然是很基础的,很多东西都讲的不够…...
跨境电商如何通过软文建立品牌形象?
在全球产业链结构重塑后的今天,越来越多的企业意识到想要可持续发展,就需要在建立品牌形象,在用户心中留下深刻印象,那么应该如何有效建立品牌形象呢?可以利用软文来打造品牌形象,接下来媒介盒子就告诉大家…...
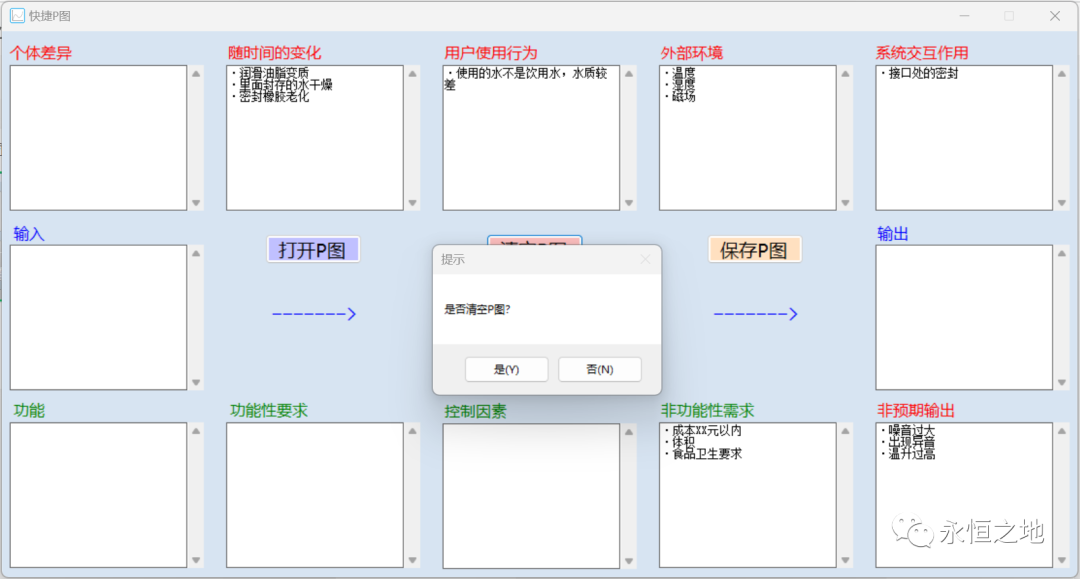
我做了一个简易P图(参数图)分析软件
P图(即参数图,Parameter Diagram),是一个结构化的工具,帮助大家对产品更好地进行分析。 典型P图格式 P图最好是和FMEA软件联动起来,如国可工软的FMEA软件有P图分析这个功能。 单纯的P图分析软件很少,为了方便做P图分…...
:状态,按键分区,算子状态,状态后端。容错机制,检查点,保存点。状态一致性。flink与kafka整合)
209.Flink(四):状态,按键分区,算子状态,状态后端。容错机制,检查点,保存点。状态一致性。flink与kafka整合
一、状态 1.概述 算子任务可以分为有状态、无状态两种。 无状态:filter,map这种,每次都是独立事件有状态:sum这种,每次处理数据需要额外一个状态值来辅助。这个额外的值就叫“状态”2.状态的分类 (1)托管状态(Managed State)和原始状态(Raw State) 托管状态就是由…...
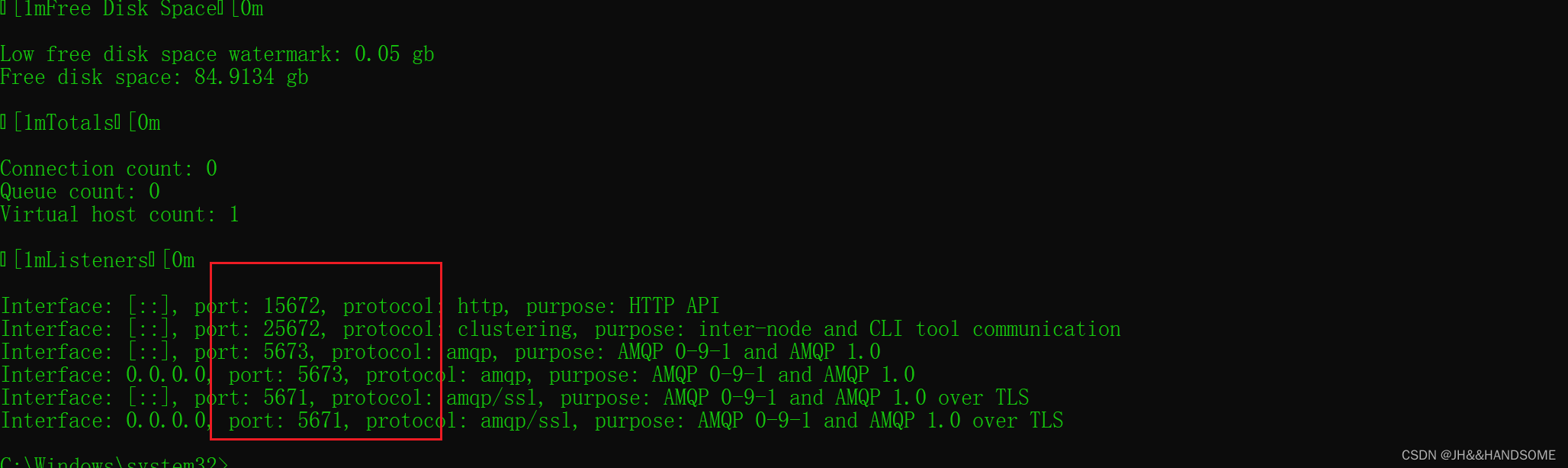
rabbitmq查看节点信息命令失败
不影响访问rabbitmq,但是无法使用 命令查看节点信息 等 查看节点信息命令:rabbitmq-diagnostics status --node rabbitJHComputer Error: unable to perform an operation on node ‘rabbitJHComputer‘. Please see diagnostics informatio rabbitmq-…...
c语言动态内存分布
前言: 随着我们深入的学习c语言,之前使用的静态内存分配已经难以满足我们的实际需求。比如前面我们的通讯录功能的实现,如果只是静态内存分配,那么也就意味着程序开始的内存分配大小就是固定的,应该开多大的空间呢&am…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...