来 来 来 国家开放大学模拟题型 训练
试卷代号:2110
行政法与行政诉讼法 参考试题
一、单项选择题(每小题只有一项正确答案,请将正确答案的序号填在括号内。每小题2分,共20分)
1.下列案件中属于行政诉讼受案范围的是( )。
A.因人民政府对某工作人员的开除决定引起的纠纷
B.因政府制定关于植树造林的规范性文件引起的纠纷
C.因某国家机关对其内部某公务员的降职决定引起的纠纷
D.因人民政府责令某企业停产治理环境污染的决定引起的纠纷
2.行政主体不明确或者明显超越相应职权的行政行为,属于( )。
A.有效的行政行为 B.无效的行政行为
C.可撤销的行政行为 D.可废止的行政行为
3.下列有关行政主体的说法,正确的是( )。
A.只有行政机关才能成为行政主体
B.行政主体还包括执行公务的国家公务员
C.行政主体是能以自己名义实施行政权的组织
D.只要是行政机关任何时候都具有行政主体资格
4.市场监督管理机关颁发营业执照,属于行使( )。
A.行政处置权 B.行政合同的签订权
C.行政许可权 D.行政确认权
5.不具有行政立法权的是( )。
A.教育部 B.河南省人民政府办公厅
C.深圳市人民政府 D.国家税务总局
6.行政许可公开原则不包括( )。
A.公开实施主体 B.公开实施程序
C.公开实施期限 D.公开国家秘密
7.依据《行政处罚法》的规定,行政处罚一般由( )的行政机关管辖。
A.地方人民政府所在地 B.行政机关所在地
C.行政相对人住所地 D.违法行为发生地
8.根据《行政诉讼法》的规定,经复议的案件,复议机关改变原行政行为的,被告是( )。
A.复议机关 B.由上级行政机关指定
C由原告认定 D.作出原行政行为的行政机关
9.行政行为已完成原定目标、任务,实现了国家的行政管理目的,应予以( )。
A.宣布无效 B.撤销
C.废止 D.变更
10.根据《行政诉讼法》的规定,行政处罚明显不当,或者其他行政行为涉及对款额的确
定、认定确有错误的,人民法院可以判决( )。
A.变更 B.无效
C.撤销 D.确认
二、多项选择题(每小题有两个或者两个以上的正确答案,请将正确答案的序号填在括号内。每小题3分,共15分)
11.行政行为的生效,主要包括( )。
A.即时生效 B.告知生效
C.受领生效 D.附条件生效
12.根据《行政许可法》规定,下列事项中可以设定行政许可的是( )。
A.直接涉及国家安全、公共安全、经济宏观调控、生态环境保护以及直接关系人身健
康、生命财产安全等特定活动,需要按照法定条件予以批准的事项
B.有限自然资源开发利用、公共资源配置以及直接关系公共利益的特定行业的市场
准入等,需要赋予特定权利的事项
C.行业组织或者中介机构能够自律管理的事项
D.市场竞争机制能够有效调节的事项
13.行政行为通常具有以下法律效力( )。
A.公定力 B.确定力
C.拘束力 D.执行力
14.诉讼期间,不停止行政行为的执行。但有下列情形之一的,裁定停止执行( )
A.原告认为需要停止执行的
B.被告认为需要停止执行的
C.人民法院认为该行政行为的执行会给国家利益、社会公共利益造成重大损害的
D.法律、法规规定停止执行的
15.根据《公务员法》规定,可以引起公务员法律关系发生的是( )。
A.选任 B.委任
C.聘任 D.考任
三、名词解释(每小题5分,共20分)
16.行政法
17.行政行为
18.行政奖励
19.行政强制措施
四、简答题(每小题10分,共30分)
20.简述行政处罚的基本原则。
21.简述我国公务员的义务。
22.简述行政程序的特征。
五、案例分析题(15分)
23.案情介绍:张某是个体工商户,经营一个小食品店,两年来一直未向税务机关交足税款。此事被乡政府在一次对市场经营的食品质量进行检查时发现。乡政府以自己的名义给张某下达两次补交税款1100元的通知,张某均未按通知补税。2015年5月24日乡政府扣押了张某的一台电冰箱与部分食品,当时未办理任何手续。张某对此不服,在同年7月2日向县人民法院提起诉讼。县人民法院受理了此案。
问题:
(1)乡政府下达补交税款通知的行为合法吗?为什么?
(2)县人民法院对乡政府的行为,应当如何判决?
(3)对张某不按规定纳税的违法行为,县人民法院将怎样处理?
相关文章:

来 来 来 国家开放大学模拟题型 训练
试卷代号:2110 行政法与行政诉讼法 参考试题 一、单项选择题(每小题只有一项正确答案,请将正确答案的序号填在括号内。每小题2分,共20分) 1.下列案件中属于行政诉讼受案范围的是( )。 A.因人民政府对某工作人员的…...
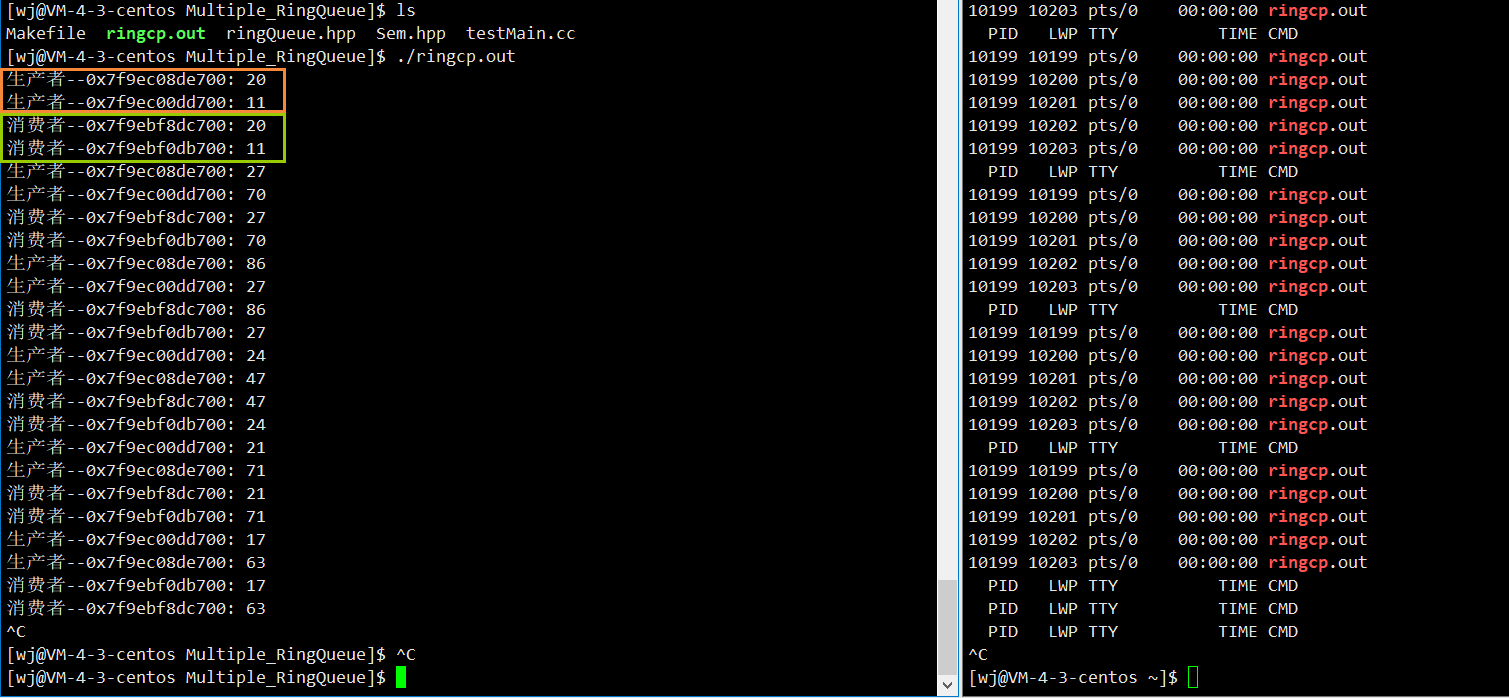
【ONE·Linux || 多线程(二)】
总言 多线程:生产者消费者模型与两种实现方式(条件变量、信号量)、线程池。 文章目录 总言4、生产者消费者模型4.1、基本概念4.2、基于BlockingQueue的生产者消费者模型(理解条件变量)4.2.1、单生产者单消费者模式&am…...

pandas.DataFrame.to_excel:在同一个sheet内追加数据
参考了这篇文章的方法 pandas to_excel:写入数据,在同一个sheet中追加数据,写入到多个sheet里,基本逻辑是: 通过数据框获取到该Excel表的行数 df_rows,然后将需要存储的数据,限制开始写入的行数,…...

基于卷积神经网络的图像识别技术研究与实践
基于卷积神经网络的图像识别技术研究与实践 卷积神经网络(CNN)是一种深度学习模型,它在图像识别领域取得了显著的成果。本文旨在探讨基于卷积神经网络的图像识别技术研究与实践。 一、卷积神经网络概述 卷积神经网络是一种深度学习模型&am…...

Linux防火墙之--SNAT和DNAT
1.SNAT是什么 SNAT又称源地址转换。源地址转换是内网地址向外访问时,发起访问的内网ip地址转换为指定的ip地址(可指定具体的服务以及相应的端口或端口范围),这可以使内网中使用保留ip地址的主机访问外部网络,即内网的多…...

Bean注入方式:@Autowired、@Resource的区别
Autowired 和 Resource 的区别是什么? Autowired 属于 Spring 内置的注解,默认的注入方式为 byType(根据类型进行匹配),也就是说会优先根据接口类型去匹配并注入 Bean (接口的实现类)。 这会有…...

软件设计原则 1小时系列 (C++版)
文章目录 前言基本概念 Design Principles⭐单一职责原则(SRP) Single Responsibility PrincipleCode ⭐里氏替换原则(LSP) Liskov Substitution PrincipleCode ⭐开闭原则(OCP) Open Closed PrincipleCode ⭐依赖倒置原则(DIP) Dependency Inversion PrincipleCode ⭐接口隔离…...
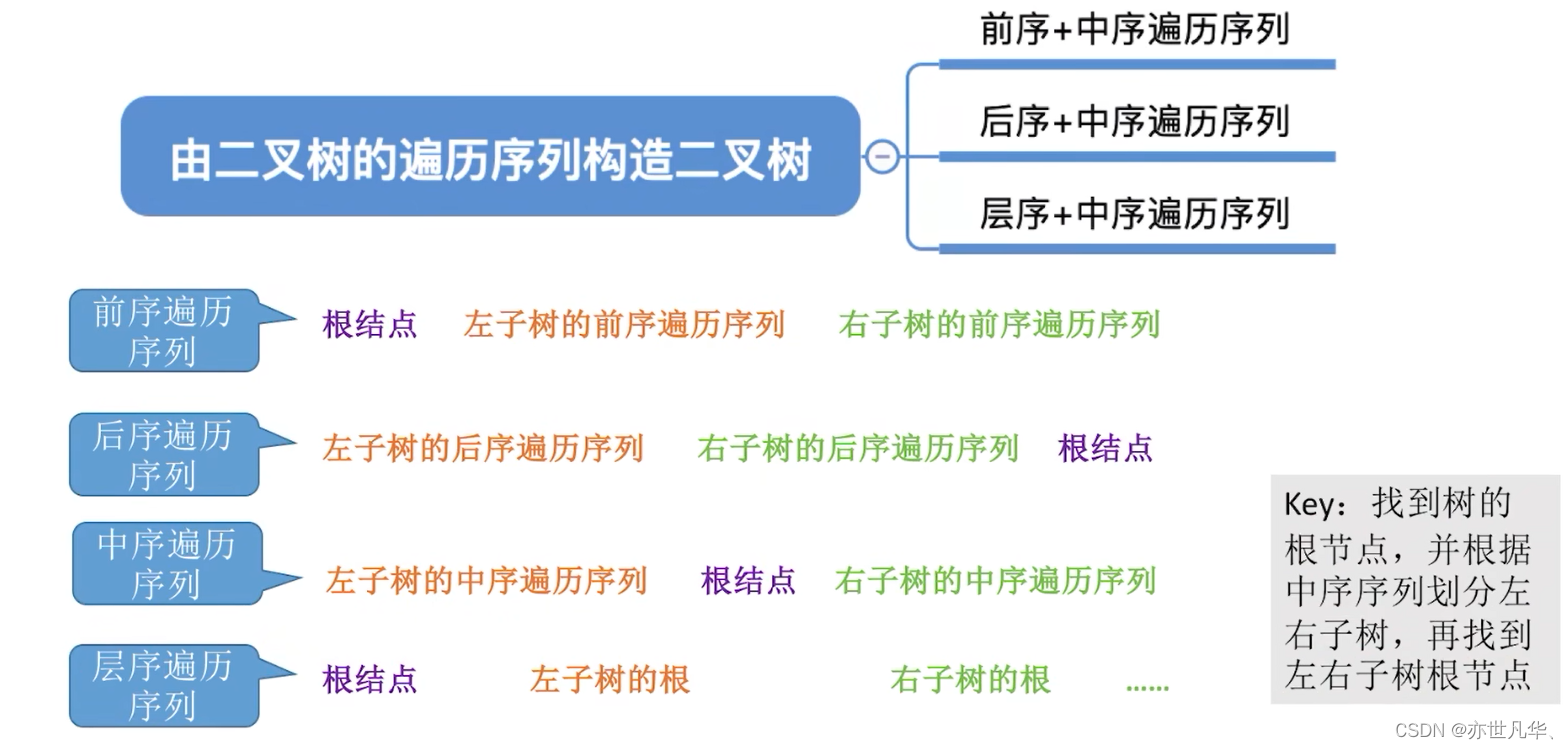
数据结构--》解锁数据结构中树与二叉树的奥秘(一)
数据结构中的树与二叉树,是在建立非线性数据结构方面极为重要的两个概念。它们不仅能够模拟出生活中各种实际问题的复杂关系,还常被用于实现搜索、排序、查找等算法,甚至成为一些大型软件和系统中的基础设施。 无论你是初学者还是进阶者&…...
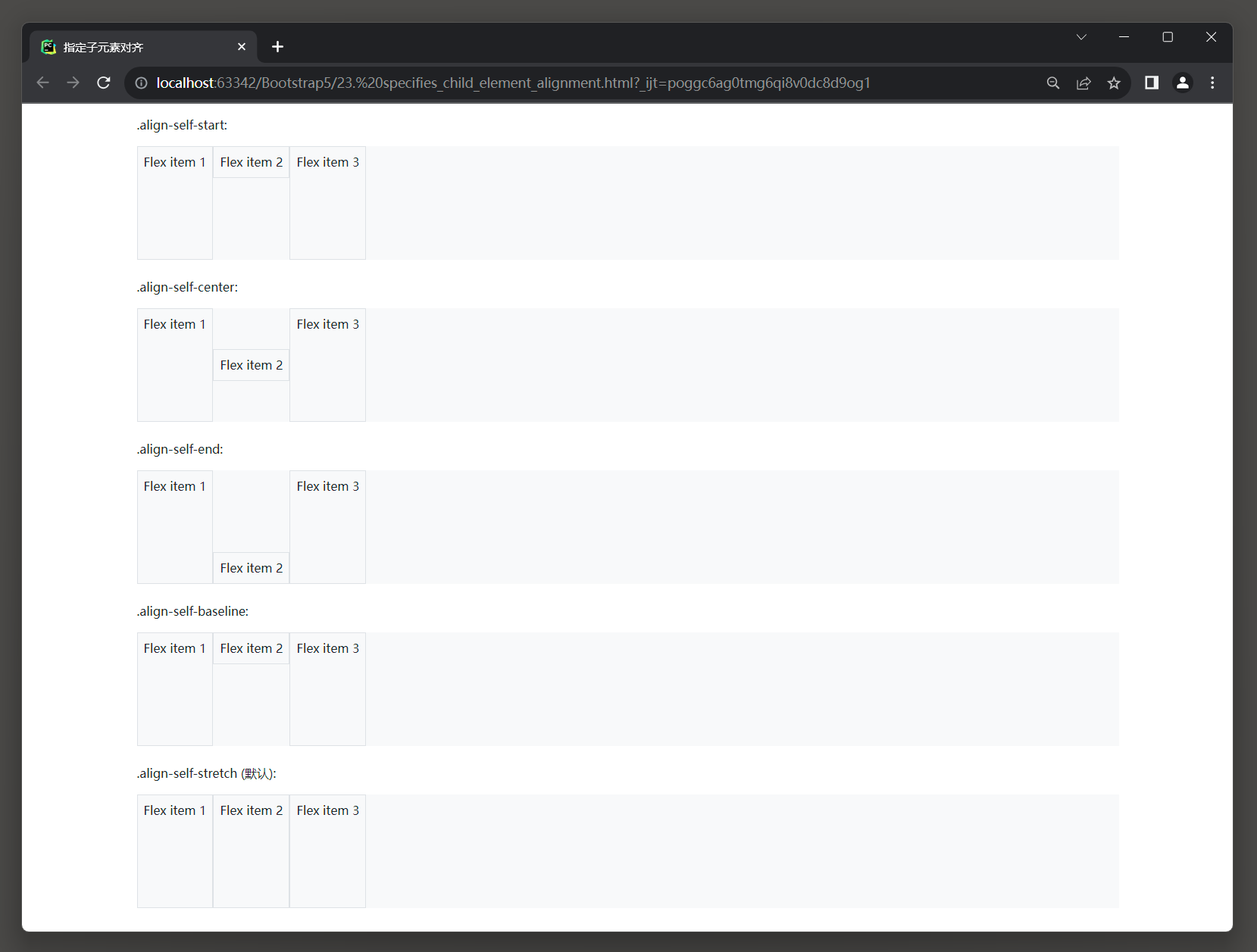
23.4 Bootstrap 框架5
1. 背景颜色 1.1 背景颜色样式 在Bootstrap 5中, 可以使用以下类来设置背景颜色: * 1. .bg-primary: 设置为主要的背景颜色(#007bff, 深蓝色). * 2. .bg-secondary: 设置为次要的背景颜色(#6c757d, 灰色). * 3. .bg-success: 设置为成功的背景颜色(#28a745, 绿色). * 4. …...
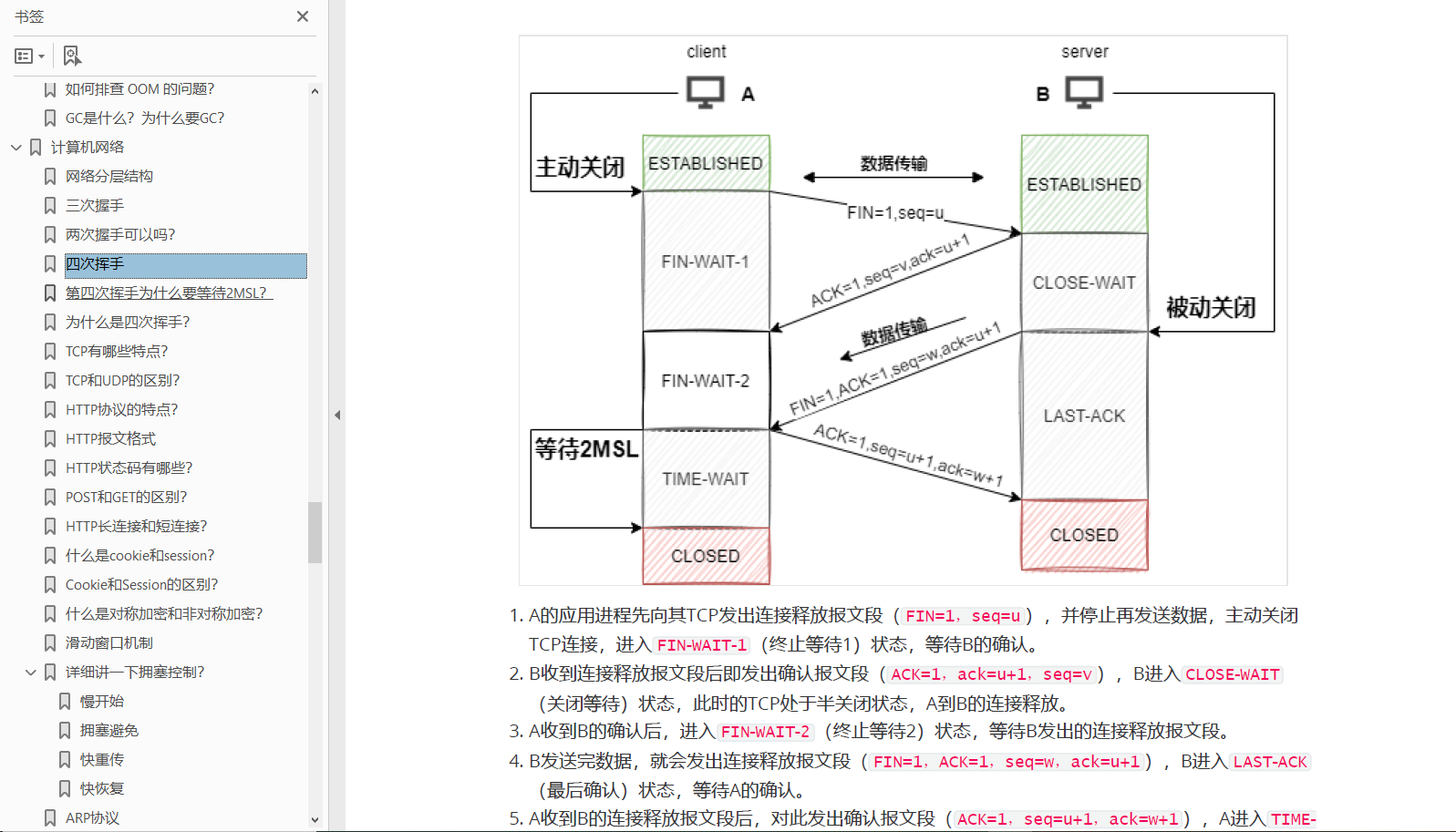
Spring源码解析——IOC属性填充
正文 doCreateBean() 主要用于完成 bean 的创建和初始化工作,我们可以将其分为四个过程: 最全面的Java面试网站 createBeanInstance() 实例化 beanpopulateBean() 属性填充循环依赖的处理initializeBean() 初始化 bean 第一个过程实例化 bean在前面一篇…...

寒露到了,冬天还会远吗?
寒露惊秋晚,朝看菊渐黄。 日复一日间,光影如梭,我们便很快将告别了秋高气爽,白日将变得幽晦, 天寒夜长,风气萧索,雾结烟愁。 还没好好体会秋高气爽,寒露就到了。 今天晚上9点多,我们…...

科普②| 大数据有什么用?大数据技术的应用领域有哪些?
1、提供个性服务很多人觉得大数据好像离我们很远,其实我们在日常所使用的智能设备,就需要大数据的帮助。比如说我们运动时候戴的运动手表或者是运动手环,就可以在我们平时运动的时候,帮助我们采集运动数据及热量消耗情况。进入睡眠…...

golang的切片使用总结二
如果没看golang切片的第一篇总结博客 golang的切片使用总结一-CSDN博客 ,请浏览之 举例9:make([]int, a, b)后访问下标a的元素 s : make([]int, 10, 12) v : s[10] fmt.Printf("v:%v", v) 打印结果: panic: runtime error: index …...
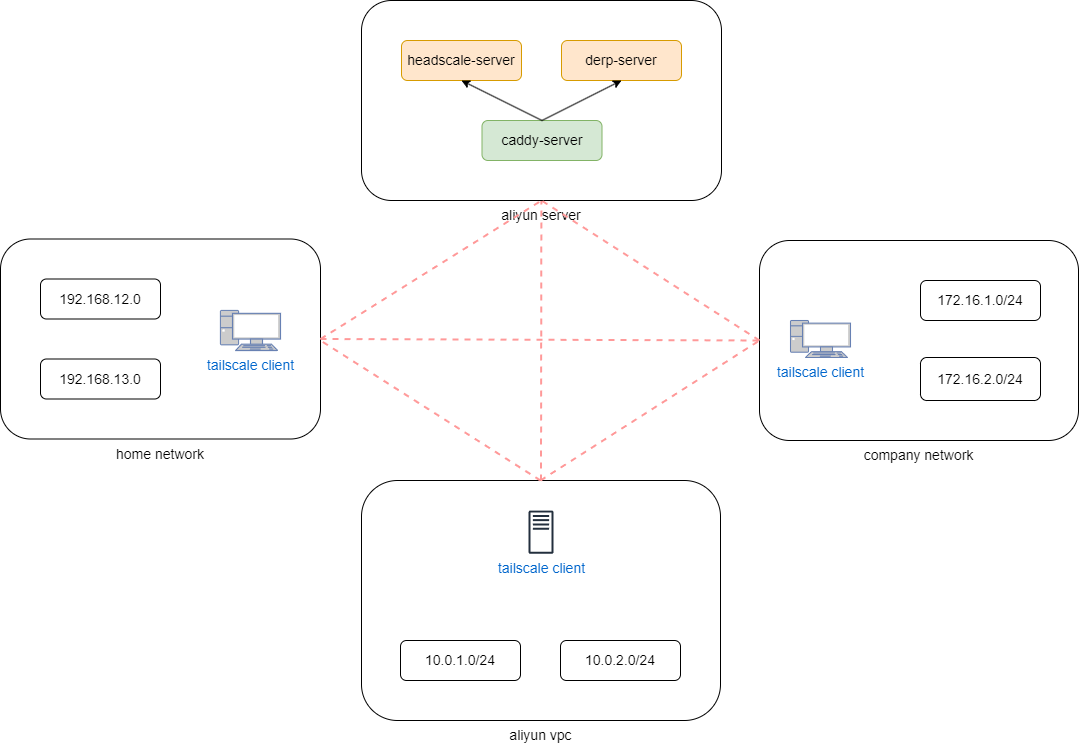
tailscale自建headscale和derp中继
tailscale derp中继服务简介 tailscale是一个基于WireGuard的零配置软件,它可以轻松地在多台设备之间建立点对点加密连接。 derp服务器是tailscale网络的重要组成部分。它作为tailscale客户端之间的中继,帮助客户端找到并连接到其他客户端设备。 但Tailscale 官方…...
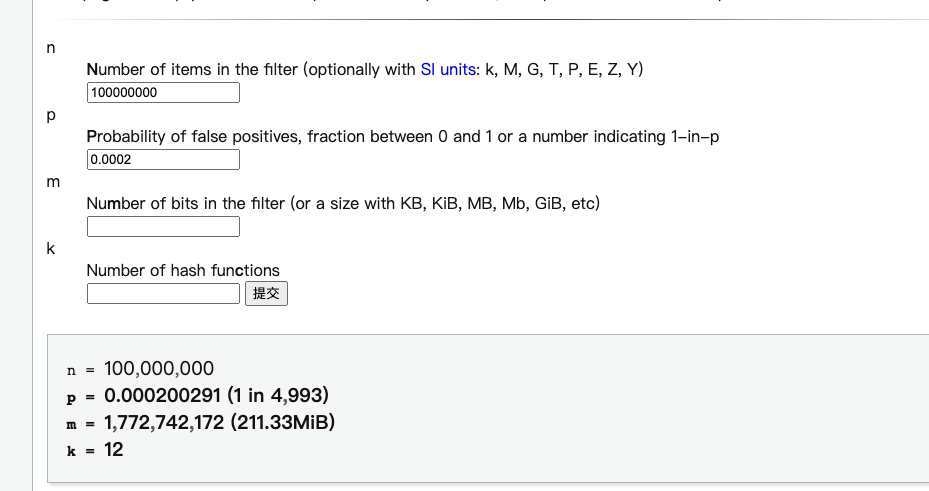
布隆过滤器的使用
布隆过滤器简介 Bloom Filter(布隆过滤器)是一种多哈希函数映射的快速查找算法。它是一种空间高效的概率型数据结构,通常应用在一些需要快速判断某个元素是否属于集合,但是并不严格要求100%正确的场合。 布隆过滤器的优势在于,利用很少的空…...

Web开发-单例模式
目录 单例模式介绍代码实现单例模式 单例模式介绍 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点。单例模式可以通过private属性实现。通过将类的构造函数设为private,可以防止类在外部被实例化。单例模式通…...
MySQL:温备份和恢复-mysqldump (4)
介绍 温备:同样是在数据库运行的时候进行备份的,但对当前数据库的操作会产生影响。(只可以读操作,不可以写操作) 温备份的优点: 1.可在表空间或数据文件级备份,备份时间短。 2.备份时数据库依然…...
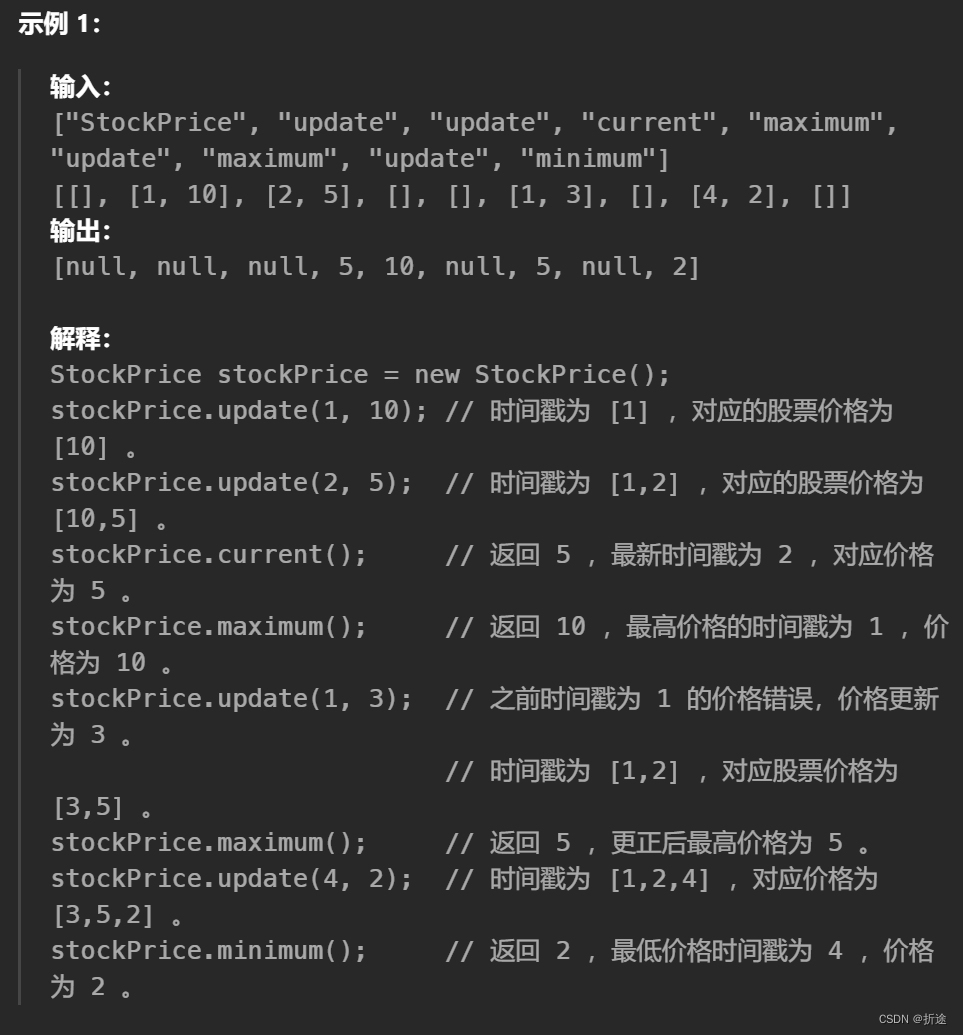
【力扣每日一题】2023.10.8 股票价格波动
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题是程序设计题,要我们实现一个类,一共是四个功能,第一个是给一个时间戳和价格,表示该…...

Linux隐藏文件或文件夹
在Linux中,以点(.)开头的文件或文件夹是隐藏文件或隐藏文件夹。要创建一个隐藏文件或文件夹,可以使用以下命令: 创建隐藏文件: touch .filename这将在当前目录下创建一个名为 “.filename” 的隐藏文件。…...
leetcode - 365周赛
一,2873.有序三元组中的最大值 I 该题的数据范围小,直接遍历: class Solution {public long maximumTripletValue(int[] nums) {int n nums.length;long ans 0;for(int i0; i<n-2; i){for(int ji1; j<n-1; j){for(int kj1; k<…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
