【Overload游戏引擎分析】从视图投影矩阵提取视锥体及overload对视锥体的封装
overoad代码中包含一段有意思的代码,可以从视图投影矩阵逆推出摄像机的视锥体,本文来分析一下原理
一、平面的方程
视锥体是用平面来表示的,所以先看看平面的数学表达。
平面方程可以由其法线N=(A, B, C)和一个点Q=(x0,y0,z0)定义,其形式为:
A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_{0})+B(y-y_{0})+C(z-z_{0})=0 A(x−x0)+B(y−y0)+C(z−z0)=0 整理变为: A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0, 其中 D = − A x 0 − B y 0 − C z 0 D=−Ax_{0}−By_{0}−Cz_{0} D=−Ax0−By0−Cz0
方程进一步可以将方程归一化:
A A 2 + B 2 + C 2 x + B A 2 + B 2 + C 2 y + C A 2 + B 2 + C 2 z + D A 2 + B 2 + C 2 = 0 \frac{A}{\sqrt{A^{2}+B^{2}+C^{2} } } x + \frac{B}{\sqrt{A^{2}+B^{2}+C^{2} } }y+\frac{C}{\sqrt{A^{2}+B^{2}+C^{2} } }z+\frac{D}{\sqrt{A^{2}+B^{2}+C^{2} } } = 0 A2+B2+C2Ax+A2+B2+C2By+A2+B2+C2Cz+A2+B2+C2D=0 写成通用格式 a x + b y + c z + d = 0 ax+by+cz+d=0 ax+by+cz+d=0
那么点 p = ( x 1 , y 1 , z 1 ) p=(x_{1}, y_{1}, z_{1}) p=(x1,y1,z1)到平面的距离为:
D = a x 1 + b y 1 + c z 1 + d D=ax_{1}+by_{1}+cz_{1}+d D=ax1+by1+cz1+d
一个平面会将空间分成两个半空间(halfspace),进一步法线的朝向的空间称为正半空间(positive halfspace),法线背离的空间称为反半空间(negative halfspace)。根据D的符号可以判断点的相对位置:
- D < 0, 点位于反半空间
- D = 0, 点位于平面上
- D > 0, 点位于正半空间
这种特性可用于判断点是否在视锥体内部。
二、OpenGL视锥体
视锥体是摄像机能看到的区域,只有在视锥体内的物体才能被看到。其由近平面、远平面与周围四个面组成,形成一个平截头体区域。

三、Overload对视锥体的封装
Overload对视锥体的封装在文件Frustum.h、Frustum.cpp中。先看其定义:
class Frustum
{
public:/*** 根据视图投影矩阵提取视锥体* @param p_viewProjection*/ void CalculateFrustum(const OvMaths::FMatrix4& _viewProjection);/*** 判断点是不是在视锥体内* @param p_x* @param p_y* @param p_z*/bool PointInFrustum(float p_x, float p_y, float _z) const;/*** 判断球是不是在视锥体内* @param p_x* @param p_y* @param p_z* @param p_radius*/bool SphereInFrustum(float p_x, float p_y, loat p_z, float p_radius) const;/*** 判断立方体是不是在视锥体内* @param p_x* @param p_y* @param p_z* @param p_size*/bool CubeInFrustum(float p_x, float p_y, float _z, float p_size) const;/*** 判断包围球是不是在视锥体内* @param p_boundingSphere* @param p_transform*/bool BoundingSphereInFrustum(const vRendering::Geometry::BoundingSphere& _boundingSphere, const OvMaths::FTransform& _transform) const;/*** 返回近平面*/std::array<float, 4> GetNearPlane() const;/*** 返回远平面*/std::array<float, 4> GetFarPlane() const;
private:float m_frustum[6][4]; // 6个平面的方程参数
};
m_frustum保存着6个平面的方程参数,为了提升操作便利性,其定义了两个枚举作为索引:
enum FrustumSide
{RIGHT = 0, // The RIGHT side of the frustumLEFT = 1, // The LEFT side of the frustumBOTTOM = 2, // The BOTTOM side of the frustumTOP = 3, // The TOP side of the frustumBACK = 4, // The BACK side of the frustumFRONT = 5 // The FRONT side of the frustum
};// 平面方程的参数索引
enum PlaneData
{A = 0, // The X value of the plane's normalB = 1, // The Y value of the plane's normalC = 2, // The Z value of the plane's normalD = 3 // The distance the plane is from the origin
};
函数的具体实现在文件Frustum.cpp中,我们先看最基础的判断点是否在视锥体内:
bool OvRendering::Data::Frustum::PointInFrustum(float x, float y, float z) const
{for (int i = 0; i < 6; i++){if (m_frustum[i][A] * x + m_frustum[i][B] * y + m_frustum[i][C] * z + m_frustum[i][D] <= 0){return false;}}return true;
}
定义视锥体的面法线都是朝外的,如果点在视锥体内,点到6个面的距离必须全部小于0。进一步判断球体是否完全在视锥体内,距离必须小于半径的负数。
最后分析一下CalculateFrustum,它是根据一个视图投影矩阵反向构建一个视锥体,具体公式怎么来的可以参考这篇文章,里面将的特别详细:
Fast Extraction of Viewing Frustum Planes from the World View-Projection Matrix
其本身的代码没啥好说的,无非就是公式的翻译。
相关文章:

【Overload游戏引擎分析】从视图投影矩阵提取视锥体及overload对视锥体的封装
overoad代码中包含一段有意思的代码,可以从视图投影矩阵逆推出摄像机的视锥体,本文来分析一下原理 一、平面的方程 视锥体是用平面来表示的,所以先看看平面的数学表达。 平面方程可以由其法线N(A, B, C)和一个点Q(x0,…...

vue全局事件总线是什么?有什么用?解决了什么问题,与pinia有什么区别?
全局事件总线快速入门 概念基本概念(是什么?)核心概念 核心特性和优势(有什么用?)解决了什么问题?主要优势是什么? 案例演示?传递数据-案例演示传递事件-案例演示 与pinia有什么区别?…...
【debian 12】:debian系统切换中文界面
目录 目录 项目场景 基础参数 原因分析 解决方案 1.ctrlaltT 打开终端 2.查询当前语言环境(我的已经设置成了中文 zh_CN.UTF-8) 3.打开语言配置界面 4.最后一步:重启 不要放弃任何一个机会! 项目场景: 这两…...
)
es官方为我们提供的堆内存保护机制-熔断器( breaker )
总熔断器(相当于似乎总闸) 参数: indices.breaker.total.use_real_memory 默认值:true 在 elasticsearch.yml中配置。 参数: indices.breaker.total.limit 如果 indices.breaker.total.use_real_memory : true, in…...

靶场通关记录
OSCP系列靶场-Esay-CyberSploit1 总结 getwebshell → 源码注释发现用户名 → robots.txt发现base64密码 → SSH登录 提 权 思 路 → 内网信息收集 → 发现发行版本有点老 → 内核overlayfs提权 准备工作 启动VPN 获取攻击机IP > 192.168.45.220 启动靶机 获取目标机器I…...
全网最新最全的软件测试面试题
一、前言 与开发工程师相比,软件测试工程师前期可能不会太深,但涉及面还是很广的。 在一年左右的实习生或岗位的早期面试中,主要是问一些基本的问题。 涉及到的知识主要包括MySQL数据库的使用、Linux操作系统的使用、软件测试框架问题、测试…...
如何列出 Ubuntu 和 Debian 上已安装的软件包
当你安装了 Ubuntu 并想好好用一用。但在将来某个时候,你肯定会遇到忘记曾经安装了那些软件包。 这个是完全正常。没有人要求你把系统里所有已安装的软件包都记住。但是问题是,如何才能知道已经安装了哪些软件包?如何查看安装过的软件包呢&a…...

图论---最小生成树问题
在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。解决最小生成树问题一般有两种算法:Kruskal算法和Prim算法。 Kruskal算法 原理:基本思想是从小到大加入边,是个贪心算法。我们将图中的每个边按…...

elementplus 时间范围选择器限制选择时间范围
<el-date-pickerv-model"form.time" type"daterange"range-separator"-"start-placeholder"开始时间"end-placeholder"结束":disabled-date"disabledDate"calendar-Change"calendarChange" />co…...
【网络】抓包工具Wireshark下载安装和基本使用教程
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_Linux,大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的帮助…...

Metasequoia 4 水杉3D建模工具 附序列号
Metasequoia 4是一款非常强大的3D水杉建模工具,它基于多边形建模技术,可以用于创建各种对象并支持多种第三方3DCG软件的文件格式,是一款非常适合从爱好到业务,支持3D电脑绘图,3D印刷,游戏开发等的3D建模软件…...

股票杠杆交易平台排名:淘配网推荐的十大平台
在投资世界中,股票杠杆交易一直以其提供更高回报机会的吸引力而备受欢迎。随着市场的不断发展,出现了越来越多的股票杠杆交易平台。本文将为您介绍淘配网推荐的十大股票杠杆交易平台,并分析它们的特点。 富灯网 - 富灯网以其全面的杠杆产品和…...

CoreData + CloudKit 在初始化 Schema 时报错 A Core Data error occurred 的解决
问题现象 如果希望为 CoreData 支持的 App 增加云数据备份和同步功能,那么 CloudKit 是绝佳的选择。CloudKit 会帮我们默默处理好一切,我们基本不用为升级而操心。 不过,有时在用本地 CoreData NSManagedObjectModel 初始化 iCloud 中的 Schema 时会发生如下错误: Error …...
修炼k8s+flink+hdfs+dlink(三:安装dlink)
一:mysql初始化。 mysql -uroot -p123456 create database dinky; grant all privileges on dinky.* to dinky% identified by dinky with grant option; flush privileges;二:上传dinky。 上传至目录/opt/app/dlink tar -zxvf dlink-release-0.7.4.t…...
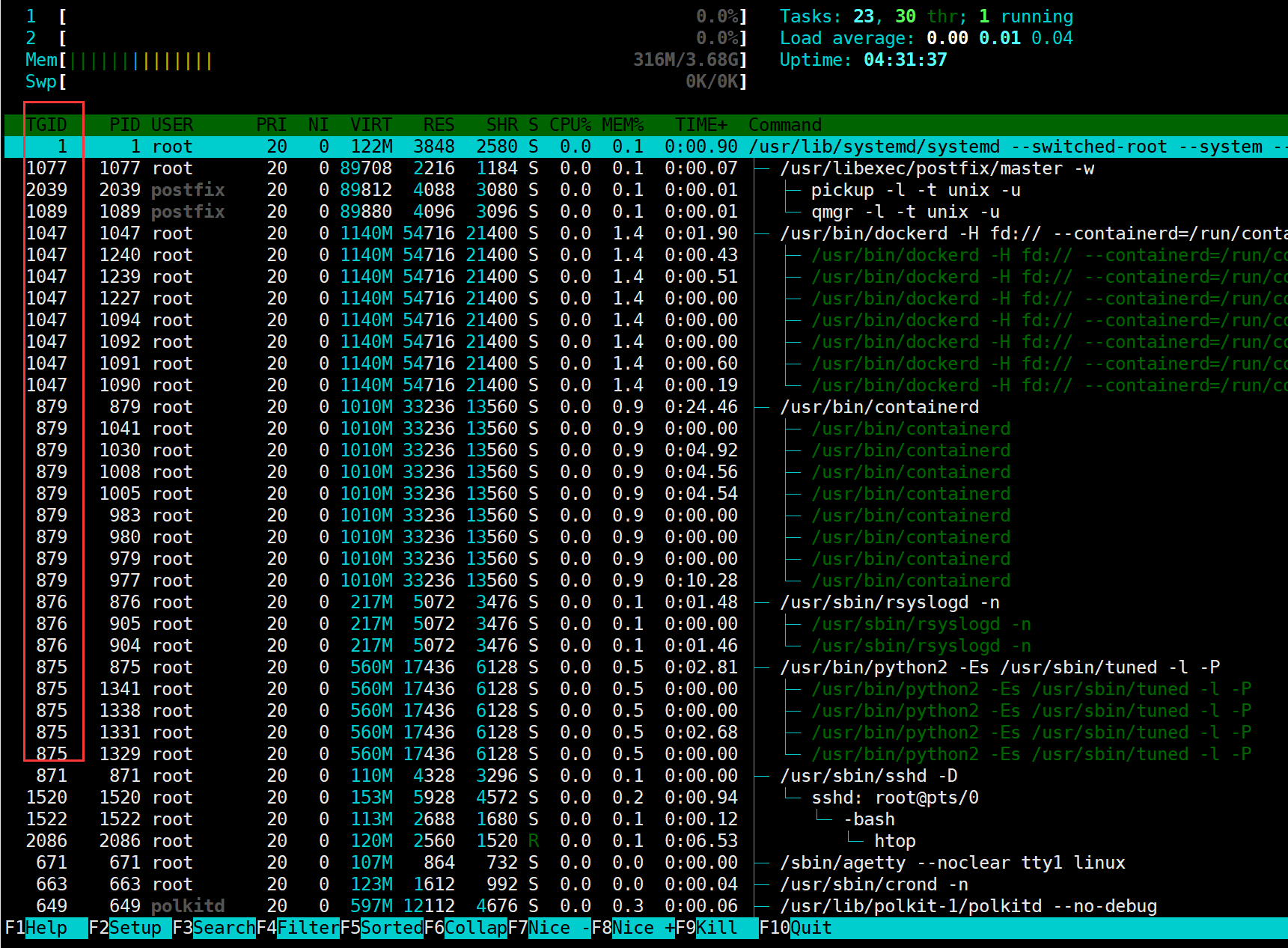
Linux 系统性能瓶颈分析(超详细)
Author:rab 目录 前言一、性能指标1.1 进程1.1.1 进程定义1.1.2 进程状态1.1.3 进程优先级1.1.4 进程与程序间的关系1.1.5 进程与进程间的关系1.1.6 进程与线程的关系 1.2 内存1.2.1 物理内存与虚拟内存1.2.2 页高速缓存与页写回机制1.2.3 Swap Space 1.3 文件系统1…...
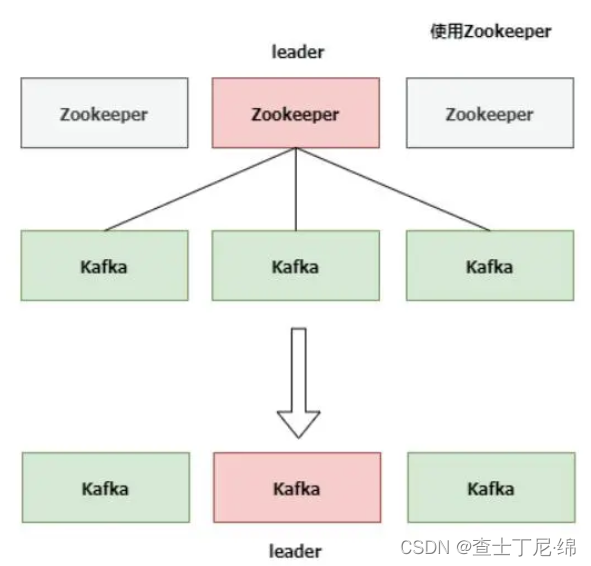
kafka与zookeeper的集群
基础配置 systemctl stop firewalld && systemctl disable firewalld setenforce 0 sed -i s/SELINUXenforcing/SELINUXdisabled/ /etc/selinux/configvi /etc/hosts ip1 node1 ip2 node2 ip3 node3zookeeper介绍 zookeeper是一个分布式的协调服务,主要用…...
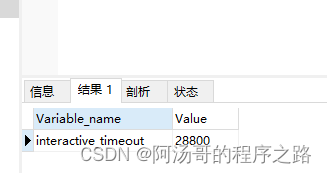
sqlalchemy 连接池
报错 sqlalchemy.exc.TimeoutError: QueuePool limit of size 100 overflow 10 reached, connection timed out, timeout 30 (Background on this error at: http://sqlalche.me/e/3o7r) 查看数据库未活动超时时间 show variables like "interactive_timeout";一般…...
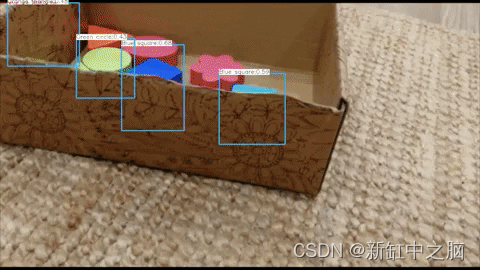
用Blender制作YOLO目标检测器训练数据
推荐:用 NSDT编辑器 快速搭建可编程3D场景 本文将介绍一种非常有吸引力的机器学习训练数据的替代方案,用于为给定的特定应用程序收集数据。 无论应用程序类型如何,这篇博文都旨在向读者展示使用 Blender 等开源资源生成合成数据(S…...
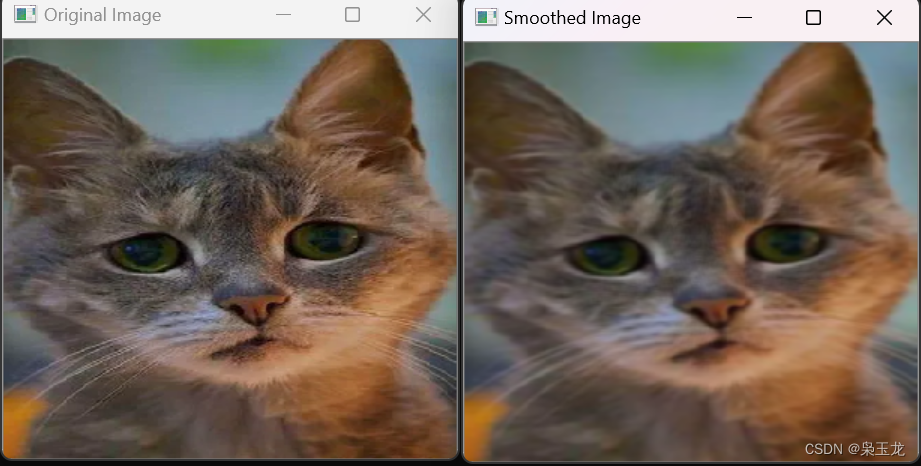
c++视觉处理---均值滤波
均值滤波 cv::blur()函数是OpenCV中用于应用均值滤波的函数。均值滤波是一种简单的平滑技术,它计算每个像素周围像素的平均值,并用该平均值替代原始像素值。这有助于降低图像中的噪声,并可以模糊图像的细节。 以下是cv::blur()函数的基本用…...

QT基础入门——Qt事件(五)
前言: 事件(event)是由系统或者 Qt 本身在不同的时刻发出的。当用户按下鼠标、敲下键盘,或者是窗口需要重新绘制的时候,都会发出一个相应的事件。一些事件在对用户操作做出响应时发出,如键盘事件等&#x…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
