【Pytorch笔记】4.梯度计算
深度之眼官方账号 - 01-04-mp4-计算图与动态图机制
前置知识:计算图
可以参考我的笔记:
【学习笔记】计算机视觉与深度学习(2.全连接神经网络)
计算图
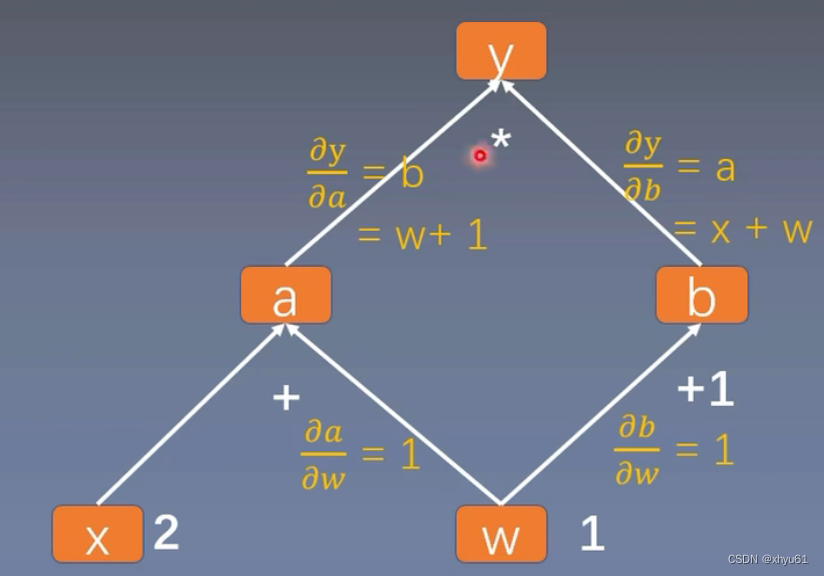
以这棵计算图为例。这个计算图中,叶子节点为x和w。
import torchw = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)# 调用backward()方法,开始反向求梯度
y.backward()
print(w.grad)print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)
print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)
输出:
tensor([5.])
is_leaf:True True False False False
gradient:tensor([5.]) tensor([2.]) None None None
由此可见,非叶子节点在最后不会被保留梯度。这是出于节省空间的需要而这样设计的。实际的计算图会非常大,如果每个节点都保留梯度,会占用非常大的存储空间,而这些节点的梯度对于我们学习并没有什么帮助。
如果非要看他们的梯度,可以这样操作:在a = torch.add(w, x)的后面加上一句a.retain_grad(),这样a的梯度就会被存储起来。
输出会变成:
tensor([5.])
is_leaf:True True False False False
gradient:tensor([5.]) tensor([2.]) tensor([2.]) None None
对于节点,还可以看这些节点进行的运算。grad_fn,gradient function的缩写,表示这个节点的tensor是什么运算产生的。加一句:
print("gradient function:\n", w.grad_fn, '\n', x.grad_fn, '\n', a.grad_fn, '\n', b.grad_fn, '\n', y.grad_fn)
会输出
gradient function:NoneNone<AddBackward0 object at 0x000001B1DA3651C0><AddBackward0 object at 0x000001B1DA3651F0><MulBackward0 object at 0x000001B1DA3515B0>
retain_graph
import torchw = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)a = torch.add(w, x)
a.retain_grad()
b = torch.add(w, 1)
y = torch.mul(a, b)# 调用backward()方法,开始反向求梯度
y.backward()
y.backward()
连续两次调用backward()方法,会报这样的错误:
RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.
原因是我们进行第一次backward()后,计算图就被自动释放掉了,进行第二次backward()时,没有计算图可以计算梯度,于是报错。
解决方案:backward内部添加一个参数:retain_graph=True,意思是计算完梯度后保留计算图。
# 调用backward()方法,开始反向求梯度
y.backward(retain_graph=True)
y.backward()
这样就不会报错了。
gradient
当计算图末部的节点有1个以上时,有时我们会希望他们之间的梯度有一个权重关系。这时就会用上gradient。
import torchw = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)a = torch.add(w, x)
b = torch.add(w, 1)# 不难看出,y0和y1是两个互不干扰的末部节点
y0 = torch.mul(a, b)
y1 = torch.add(a, b)# 将两个末部节点打包起来
loss = torch.cat([y0, y1], dim=0)
grad_tensors = torch.tensor([1., 2.])# 将grad_tensors中的内容作为权重,变成y0+2y1
loss.backward(gradient=grad_tensors)print(w.grad)
输出
tensor([9.])
如果把grad_tensors改成:
grad_tensors = torch.tensor([1., 3.])
输出变成:
tensor([11.])
torch.autograd.grad()
除了加减乘除法,我们还可以对torch进行求导操作。求的是 d ( o u t p u t s ) d ( i n p u t s ) \frac{d(outputs)}{d(inputs)} d(inputs)d(outputs)。
torch.autograd.grad(outputs,inputs,grad_outputs=None,retain_graph=None,create_graph=False)
outputs和inputs已在上述定义中给出;
grad_outputs:多梯度权重;
retain_graph:保留计算图;
create_graph:创建计算图。
import torch# y = x ** 2
x = torch.tensor([3.], requires_grad=True)
y = torch.pow(x, 2)# grad_1 = dy / dx = 2x = 6
grad_1 = torch.autograd.grad(y, x, create_graph=True)
print(grad_1)# grad_2 = d(dy / dx) / dx = 2
grad_2 = torch.autograd.grad(grad_1, x)
print(grad_2)
输出
(tensor([6.], grad_fn=<MulBackward0>),)
(tensor([2.]),)
autograd注意事项
1.梯度不会自动清零
import torchw = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)for i in range(4):a = torch.add(w, x)b = torch.mul(w, x)y = torch.mul(a, b)y.backward()print("w's grad: ", w.grad)# w.grad.zero_()
输出:
w's grad: tensor([8.])
w's grad: tensor([16.])
w's grad: tensor([24.])
w's grad: tensor([32.])
由此可以看出,在不加上注释掉的那一行时,梯度在w处是不断累积的。而如果我们把print后面的那句w.grad.zero_()加上,输出就会变成:
w's grad: tensor([8.])
w's grad: tensor([8.])
w's grad: tensor([8.])
w's grad: tensor([8.])
w.grad.zero_()的意思就是把w处积累的梯度清零。
2.依赖于叶子节点的节点,requires_grad默认为True
可以从上面的代码中发现,我们只有在定义w和x两个tensor时,设置requires_grad为True。这个参数在定义tensor时默认为False。后面我们的a、b、y都没有设置这个参数。
如果我们定义w和x的时候不加上requires_grad=True,那么y.backward()这一步就会报错,因为我们的预设,这两个tensor不需要梯度,于是就无法求梯度。而w和x是我们计算图上的叶子节点,所以必须加上requires_grad=True。
而后面通过w和x延伸定义出的a、b、y,由于依赖的w、x的requires_grad是True,那么a、b、y的这个参数也被默认设置为了True,不需要我们手动添加。
3.叶子节点不可执行in-place操作
计算图上叶子节点处的tensor不能进行原地修改。
什么是in-place操作?
t = torch.tensor([1., 2.])
t.add_(3.)
print(t)
输出
tensor([4., 5.])
torch.Tensor.add_就是torch.add的in-place版本。所谓in-place,就是在tensor上进行原地修改。大部分的torch.tensor的运算,名字后面加一个下划线,就变成inplace操作了。
再比如求绝对值:
t = torch.tensor([-1., -2.])
t.abs_()
print(t)
输出
tensor([1., 2.])
知道什么是in-place操作后,我们尝试一下在requires_grad=True的叶子节点上原地修改,代码如下:
import torchw = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)a = torch.add(w, x)
b = torch.mul(w, x)
y = torch.mul(a, b)w.add_(1)y.backward()
报错信息:
RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.
相关文章:

【Pytorch笔记】4.梯度计算
深度之眼官方账号 - 01-04-mp4-计算图与动态图机制 前置知识:计算图 可以参考我的笔记: 【学习笔记】计算机视觉与深度学习(2.全连接神经网络) 计算图 以这棵计算图为例。这个计算图中,叶子节点为x和w。 import torchw torch.tensor([1.]…...
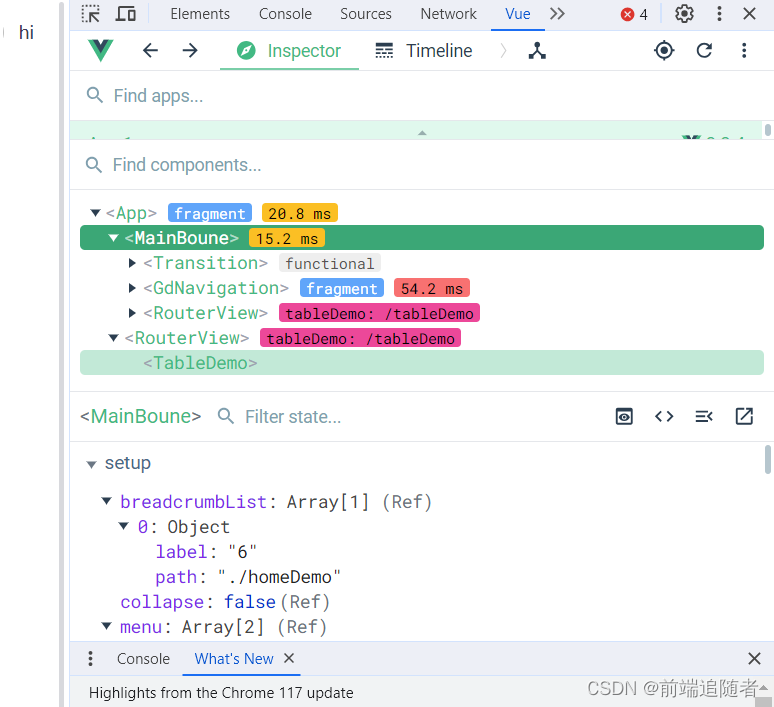
浏览器安装vue调试工具
下载扩展程序文件 下载链接:链接: 下载连接网盘地址, 提取码: 0u46,里面有两个crx,一个适用于vue2,一个适用于vue3,可根据vue版本选择不同的调试工具 crx安装扩展程序不成功,将文件改为rar文件然后解压 安装…...

C/C++学习 -- RSA算法
概述 RSA算法是一种广泛应用于数据加密与解密的非对称加密算法。它由三位数学家(Rivest、Shamir和Adleman)在1977年提出,因此得名。RSA算法的核心原理是基于大素数的数学问题的难解性,利用两个密钥来完成加密和解密操作。 特点 …...
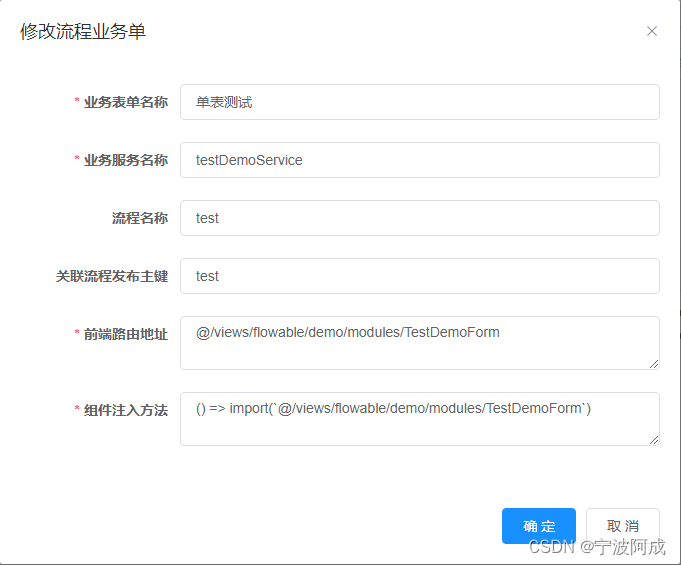
基于若依ruoyi-nbcio支持flowable流程增加自定义业务表单(一)
因为需要支持自定义业务表单的相关流程,所以需要建立相应的关联表 1、首先先建表wf_custom_form -- ---------------------------- -- Table structure for wf_custom_form -- ---------------------------- DROP TABLE IF EXISTS wf_custom_form; CREATE TABLE wf…...

面试经典 150 题 1 —(数组 / 字符串)— 88. 合并两个有序数组
88. 合并两个有序数组 方法一: class Solution { public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {for(int i 0; i<n;i){nums1[mi] nums2[i];}sort(nums1.begin(),nums1.end());} };方法二: clas…...

【大数据 | 综合实践】大数据技术基础综合项目 - 基于GitHub API的数据采集与分析平台
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...
超高频RFID模具精细化生产管理方案
近二十年来,我国的模具行业经历了快速发展的阶段,然而,模具行业作为一个传统、复杂且竞争激烈的行业,企业往往以订单为导向,每个订单都需要进行新产品的开发,从客户需求分析、结构确定、报价、设计、物料准…...

FP-Growth算法全解析:理论基础与实战指导
目录 一、简介什么是频繁项集?什么是关联规则挖掘?FP-Growth算法与传统方法的对比Apriori算法Eclat算法 FP树:心脏部分 二、算法原理FP树的结构构建FP树第一步:扫描数据库并排序第二步:构建树 挖掘频繁项集优化&#x…...

Jmeter 分布式压测,你的系统能否承受高负载?
你可以使用 JMeter 来模拟高并发秒杀场景下的压力测试。这里有一个例子,它模拟了同时有 5000 个用户,循环 10 次的情况。 请求默认配置 token 配置 秒杀接口 结果分析 但是,实际企业中,这种压测方式根本不满足实际需求。下…...

什么是浮动密封?
浮动密封也称为机械面密封或双锥密封,是一种用于各种行业和应用的特殊类型的密封装置。它旨在提供有效的密封和保护,防止污染物的进入以及旋转设备中润滑剂或液体的润滑剂泄漏。 浮动密封件由相同的金属环组成,这些金属环称为密封环…...

浅析前端单元测试
对于前端来说,测试主要是对HTML、CSS、JavaScript进行测试,以确保代码的正常运行。 常见的测试有单元测试、集成测试、端到端(e2e)的测试。 单元测试:对程序中最小可测试单元进行测试。我们可以类比对汽车的测试&…...

线上mysql表字段加不了Fail to get MDL on replica during DDL synchronize,排查记录
某天接近业务高峰期想往表里加字段加不了,报错:Fail to get MDL on replica during DDL synchronize 遂等到业务空闲时操作、还是加不了, 最后怀疑是相关表被锁了,或者有事务一直进行(可能这俩是一个意思)&…...
vue3使用element plus的时候组件显示的是英文
问题截图 这是因为国际化导致的 解决代码 import zhCn from "element-plus/es/locale/lang/zh-cn"; 或者 import zhCn from "element-plus/lib/locale/lang/zh-cn";const localezhCn<el-config-provider :locale"locale"><el-date-pic…...
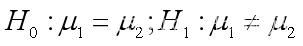
Matlab参数估计与假设检验(举例解释)
参数估计分为点估计和区间估计,在matlab中可以调用namefit()函数来计算参数的极大似然估计值和置信区间。而数据分析中用得最多的是正态分布参数估计。 例1 从某厂生产的滚珠中抽取10个,测得滚珠的直径(单位:mm)为x[…...

qt响应全局热键
QT5 QWidget响应全局热键-百度经验...

android 代码设置静态Ip地址的方法
在Android中,可以使用以下代码示例来设置静态IP地址: import android.content.Context import android.net.ConnectivityManager import android.net.LinkAddress import android.net.Network import android.net.NetworkCapabilities import android.ne…...
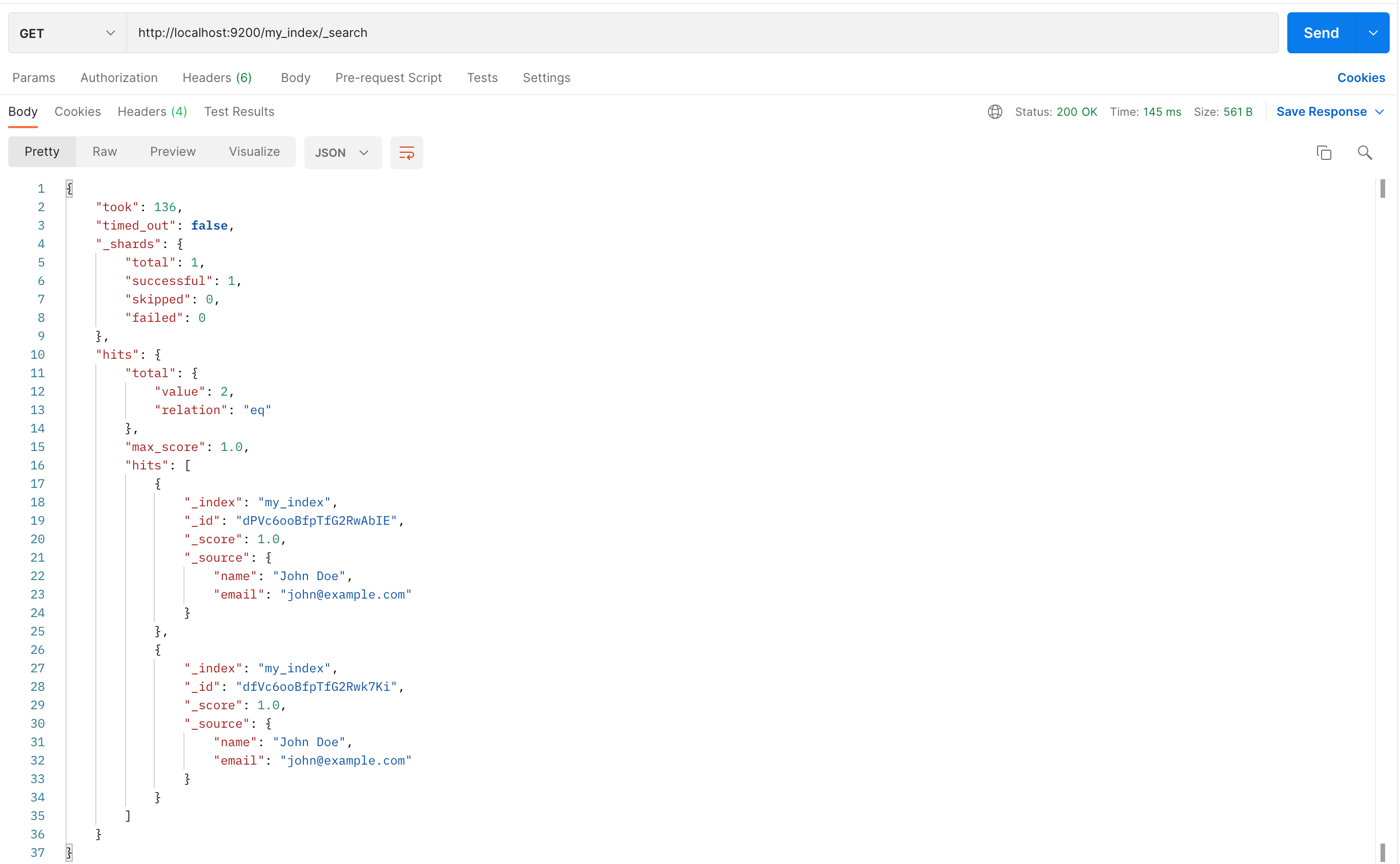
Elasticsearch安装访问
Elasticsearch 是一个开源的、基于 Lucene 的分布式搜索和分析引擎,设计用于云计算环境中,能够实现实时的、可扩展的搜索、分析和探索全文和结构化数据。它具有高度的可扩展性,可以在短时间内搜索和分析大量数据。 Elasticsearch 不仅仅是一个…...
:setState为什么使用异步机制?)
面试题-React(十):setState为什么使用异步机制?
在React中,setState的异步特性和异步渲染机制是开发者们经常讨论的话题。为什么React选择将setState设计为异步操作?异步渲染又是如何实现的?本篇博客将深入探究这些问题,通过代码示例解释为什么异步操作是React的一大亮点。 一、…...
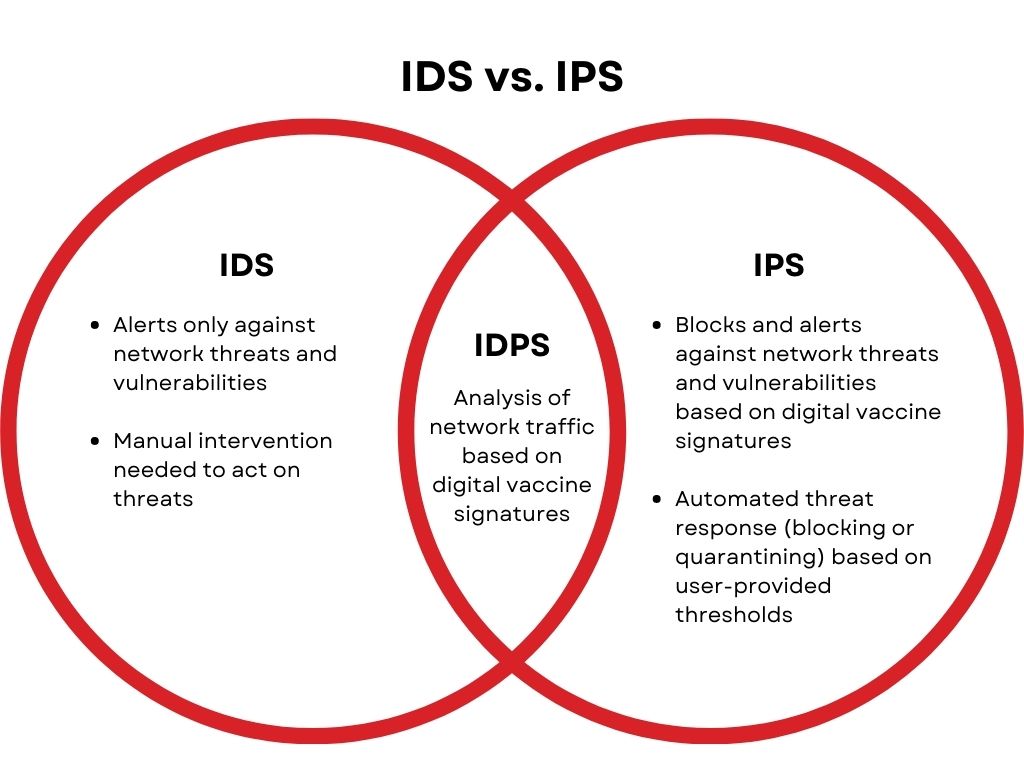
入侵防御系统(IPS)网络安全设备介绍
入侵防御系统(IPS)网络安全设备介绍 1. IPS设备基础 IPS定义 IPS(Intrusion Prevention System)是一种网络安全设备或系统,用于监视、检测和阻止网络上的入侵尝试和恶意活动。它是网络安全架构中的重要组成部分&…...

【Linux基础】Linux的基本指令使用(超详细解析,小白必看系列)
👉系列专栏:【Linux基础】 🙈个人主页:sunnyll 目录 💦 ls 指令 💦 pwd指令 💦cd指令 💦touch指令 💦mkdir指令(重要) 💦rmdir指令…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
