课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
一、简介
抗差自适应滤波:利用等价权函数和自适应因子合理的分配信息,有效地滤除钻具振动对动态姿态测量的影响。、
针对导向钻井工具动态测量受钻具振动的影响而导致测量不准确的问题,提出一种抗差自适应滤波的动态空间姿态测量方法。通过分析钻具振动对姿态测量的影响,并吸收抗差估计和自适应滤波的优点,利用抗差等价权矩阵自适应的确定量测信息,通过自适应因子调整状态模型信息对状态参数的整体贡献,从而消除钻具振动对动态姿态测量的影响,获得实时性强、精度高的姿态参数,提高钻井效率,降低钻井风险。
在实际钻井过程中,钻头切削岩层、钻柱与井壁的碰撞等会使钻具产生横向振动、纵向振动和扭转振动等,这些振动严重的影响了测量传感器输出信号的正确性。
抗差自适应滤波的基本思想是:当观测值存在异常时,对观测值采用抗差估计原则,能够控制观测异常的影响;当动力学模型存在异常误差时,将动力学模型信息作为一个整体,采用统一的自适应因子调整动力学模型信息对状态参数的整体贡献。
二、测量系统建模
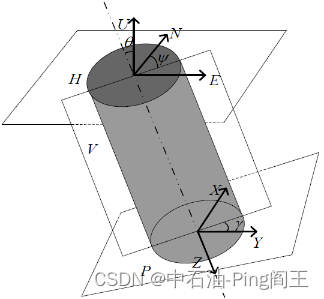
方位角 ψ \psi ψ为磁北方向沿逆时针方向到Z 轴在水平面的投影间的夹角,其范围在0°~360°之间,井斜角 θ \theta θ为钻进轴Z 轴与水平面所成的夹角,规定向下为正,反之为负,其范围为-90°~90°,工具面向角 γ \gamma γ 则为钻孔横截面内由钻孔高边到Y 轴所成的角度,范围在0°~360°之间。这样,我们就准确的定义了井下钻具的方位角 ψ \psi ψ 、井斜角 θ \theta θ 和工具面向角 γ \gamma γ ,且角度的正向都符合右手系原则。
加速度计和磁通门安装如下:
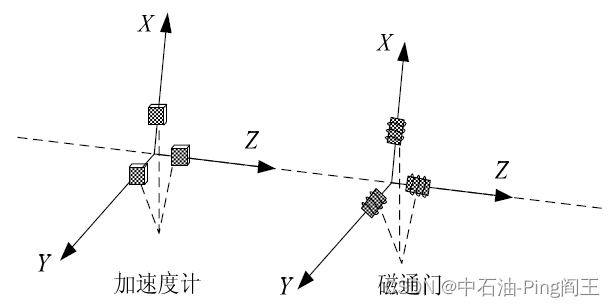
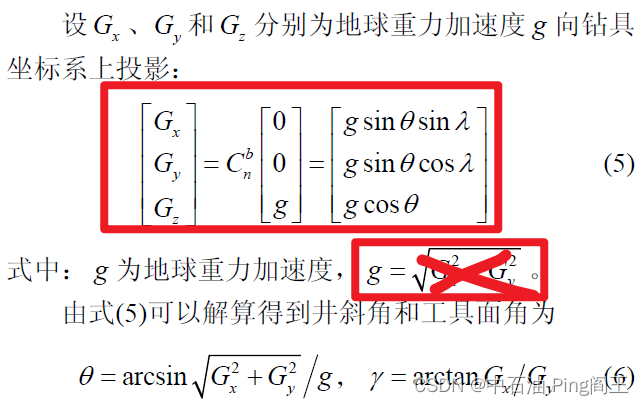
根据上述理论,建立导向钻井工具姿态测量的动
态数学模型,给出状态方程和量测方程: x k ^ = Φ k , k − 1 x k − 1 + w k \hat{x_k} = \Phi_{k,k-1}x_{k-1}+w_{k} xk^=Φk,k−1xk−1+wk
x k x_k xk 和 x k − 1 x_{k-1} xk−1分别为 t k t_k tk 和 t k − 1 t_{k-1} tk−1时刻的n 维状态参数向量, Φ k , k − 1 \Phi_{k,k-1} Φk,k−1为n× n维状态转移矩阵; w k w_k wk 为p 维动力学模型误差向量,其数学期望为0,协方差矩阵为: ∑ w k w i = { ∑ w k , k = i 0 , k ≠ i \sum_{wkwi}= \begin{cases}\sum_{wk},\quad &k=i\\0,\quad &k\neq i\end{cases} wkwi∑={∑wk,0,k=ik=i
w k wk wk为高斯白噪声序列。
设 t k t_k tk时刻的量测方程为 y k = H k x k + v k y_k=H_kx_k+v_k yk=Hkxk+vk
y k y_k yk 为 t k t_k tk时刻的m维观测向量; H k H_k Hk为m× n维测量矩阵,也称为观测矩阵; v k v_k vk为m维观测误差向量,其数学期望为0,协方差矩阵为 ∑ v k v i = { ∑ v k , k = i 0 , k ≠ i \sum_{vkvi}= \begin{cases}\sum_{vk},\quad &k=i\\0,\quad &k\neq i\end{cases} vkvi∑={∑vk,0,k=ik=i
v k v_k vk为高斯白噪声序列。在 i = k i=k i=k时, w k w_k wk 和 v k v_k vk的协方差矩阵分别为 ∑ w k \sum_{wk} ∑wk和 ∑ v k \sum_{vk} ∑vk,这里 w k w_k wk, w i w_i wi, w k w_k wk, v i v_i vi互不相关。
状态向量为: X = [ ψ , θ , γ ] T X=\begin{bmatrix}\psi,\theta,\gamma\end{bmatrix}^T X=[ψ,θ,γ]T,表明直接将钻具姿态参数作为状态向量,而
非姿态误差作为状态。
三、动态姿态测量
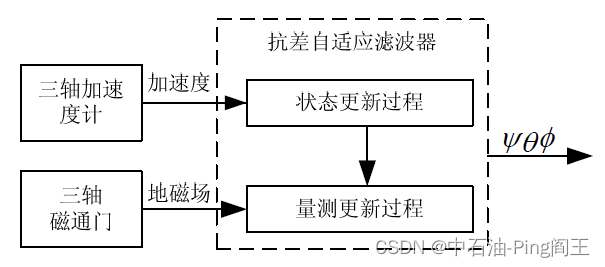
X ‾ k = Φ k , k − 1 X k − 1 ^ \overline{X}_{k} = \Phi_{k,k-1}\hat{X_{k-1}} Xk=Φk,k−1Xk−1^为系统的状态预测方程。 X ‾ k \overline{X}_{k} Xk为 t k t_k tk的状态预测方程, X k − 1 ^ \hat{X_{k-1}} Xk−1^为 t k − 1 t_{k-1} tk−1为状态估计向量。设状态预测向量 X ‾ k \overline{X}_k Xk的误差方程为: V X ‾ k = X ^ k − X ‾ k = X ^ k − Φ k , k − 1 X ^ k − 1 V_{\overline{X}_k} = \hat{X}_k-\overline{X}_k=\hat{X}_k-\Phi_{k,k-1}\hat{X}_{k-1} VXk=X^k−Xk=X^k−Φk,k−1X^k−1
V X ‾ k V_{\overline{X}_k} VXk为 t k t_k tk时刻状态预测向量 X ^ k \hat{X}_k X^k的残差向量。
残差向量和新息向量(也称为预测残差向量)分别为:
V k = H k X ^ k − Y k V_k=H_k\hat{X}_k-Y_k Vk=HkX^k−Yk V ‾ k = H k X ‾ k − Y k \overline{V}_k=H_k\overline{X}_k-Y_k Vk=HkXk−Yk
V k V_k Vk和 V ‾ k \overline{V}_k Vk的协方差矩阵为: ∑ V k = ∑ k − H k ∑ X ^ k H k T \sum_{V_k} = \sum_{k}-H_k\sum_{\hat{X}_k}H^T_k Vk∑=k∑−HkX^k∑HkT ∑ V ‾ k = ∑ k + H k ∑ V ‾ k H k T \sum_{\overline{V}_k} = \sum_{k}+H_k\sum_{\overline{V}_k}H^T_k Vk∑=k∑+HkVk∑HkT
合理地选择自适应因子不但能够自适应地平衡动力学模型预测信息与量测信息的权比,而且能够控制动力学模型扰动异常对滤波解的影响。基于预测残差误差判别统计量的抗差自适应因子函数为:
等价权矩阵为:
上式中, P ‾ k \overline{P}_k Pk为观测向量的等价权矩阵, P k = ∑ k − 1 {P}_k=\sum_{k}^{-1} Pk=∑k−1, P X ‾ k = ∑ X ‾ k − 1 P_{\overline{X}_k}=\sum_{\overline{X}_k}^{-1} PXk=∑Xk−1
α k \alpha_k αk ≤1 ,其它符号意义同前。

K k = ( H k T P ‾ k H k + α k P X ‾ k ) − 1 H k T P ‾ k K_k=(H^T_k\overline{P}_kH_k+\alpha_kP_{\overline{X}_k})^{-1}H_k^T\overline{P}_k Kk=(HkTPkHk+αkPXk)−1HkTPk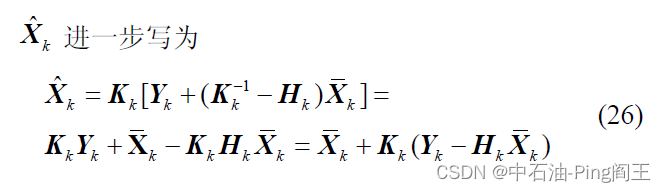
式中: K k K_k Kk 为增益矩阵,根据矩阵恒等式,可表示为: K k = α k P X ‾ k H k T ( H k α k P X ‾ k H k T + P ‾ k ) − 1 K_k=\alpha_kP_{\overline{X}_k}H_k^T(H_k\alpha_kP_{\overline{X}_k}H_k^T+\overline{P}_k)^{-1} Kk=αkPXkHkT(HkαkPXkHkT+Pk)−1
对量测信息采用抗差估计,自适应的确定观测噪声协方差矩阵,并利用自适应因子调节状态噪声的协方差矩阵,因此,可以有效的控制量测异常和动态模型噪声异常对空间状态参数估值的影响。
四、实验结果
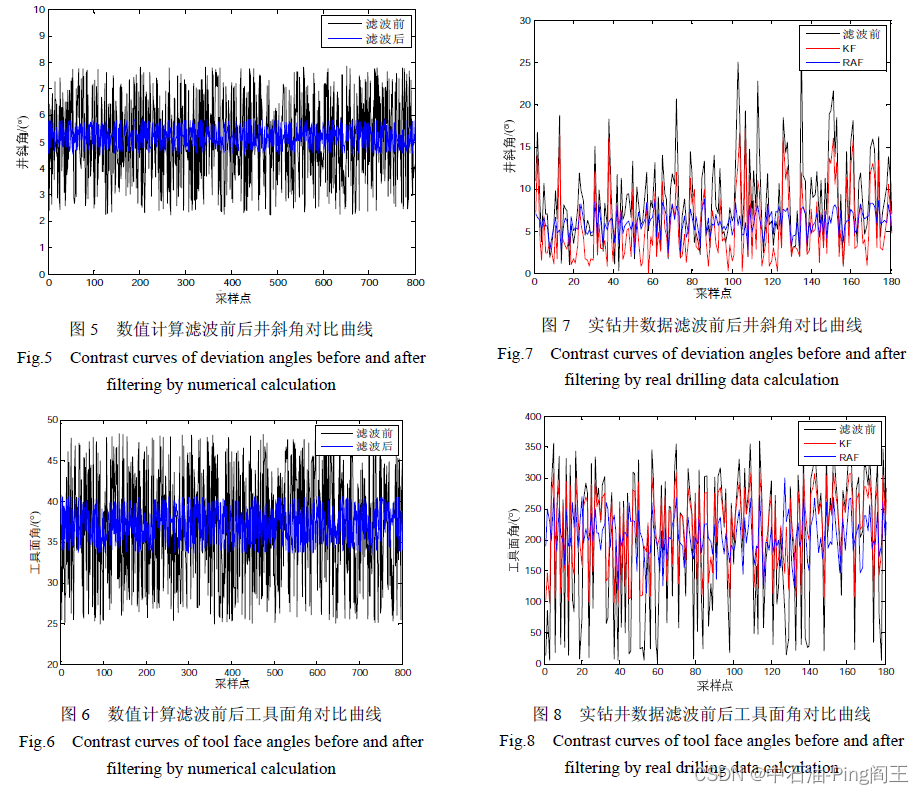
实验室地理条件为北纬34.24°,东经108.99°,地球自转角速度为15 (°)/h,磁倾角为55.4°,磁场强度为52.5 T,地球重力加速度为9.8 m/s2。在实验室条件下,根据测斜校验装置测量得到一组理想的实验数据。
五、往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法
相关文章:

课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
一、简介 抗差自适应滤波:利用等价权函数和自适应因子合理的分配信息,有效地滤除钻具振动对动态姿态测量的影响。、 针对导向钻井工具动态测量受钻具振动的影响而导致测量不准确的问题,提出一种抗差自适应滤波的动态空间姿态测量方法。通…...

一个CPU是怎么寻址的?
目录 CISC vs RISC 概念和历史 CISC vs RISC 对比举例:X86的CAS(做原子操作的) 对比举例:ARM的CAS(做原子操作的) 指令寻址 指令中的操作数的寻址方式 各语言对象内存布局对比 C内存布局 理解编译单元 Java对象内存布局 python对象模型 CPU …...

提高网站性能的10种方法:加速用户体验和降低服务器负担
在今天的数字时代,网站性能对于吸引和保留用户至关重要。一个快速加载的网站不仅提供更好的用户体验,还有助于降低服务器负担。以下是10种提高网站性能的方法,旨在加速页面加载速度和减少服务器的工作负荷。 压缩网页资源 利用压缩算法如gzi…...
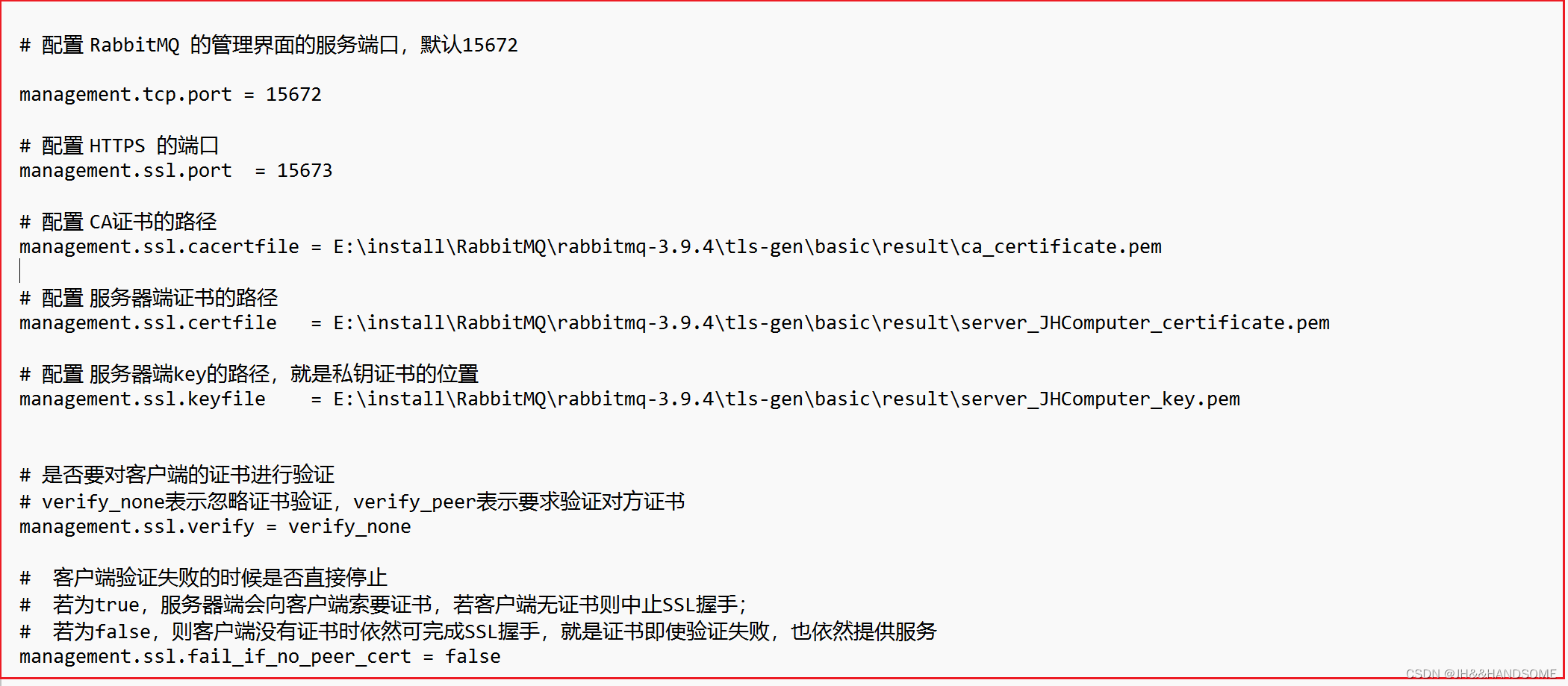
195、SpringBoot--配置RabbitMQ消息Broker的SSL 和 管理控制台的HTTPS
开启Rabbitmq的一些命令: 小黑窗输入: rabbitmq-plugins enable rabbitmq_management 启动控制台插件,就是启动登录rabbitmq控制台的页面 rabbitmq_management 代表了RabbitMQ的管理界面。 rabbitmq-server 启动rabbitMQ服务器 上面这个&…...

确定性执行
确定性执行是指在给定输入的情况下,在有限的时间内产生一致的输出。 也就是输入到输出的运行过程是确定的,输入与输出有如下关系: 输出 = f (输入)。 确定性执行主要涉及以下几个方面: 时间确定性:计算的输出始终在给定的某个时间点之前发生,即程序不能无限制地运行下去…...

docker compose 管理应用服务的常用命令
一 、docker compose 是什么 Docker Compose是一个用来管理多个关联容器的工具,可以根据配置文件自动构建、管理、编排一组容器。 Docker Compose语境下的“服务”是指一组容器共同构成的一个应用服务后端。 Docker Compose语境下的“项目”是由一个或多个应用服务…...

产品安全—CC标准 ISO/IEC 15408:2022
文章目录 1. 变化2. Part1 简介和一般模型3. Part2 安全功能组件4. Part3 安全保障组件5. Part4 评估方法和活动规范框架6. Part5 预定义的安全要求包7. 总结 1. 变化 增加了两个部分:评估方法和活动规范框架 & 预定义的安全要求包 术语已经过审查和更新&#…...
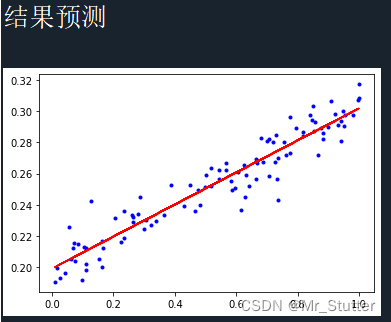
Pytorch笔记之回归
文章目录 前言一、导入库二、数据处理三、构建模型四、迭代训练五、结果预测总结 前言 以线性回归为例,记录Pytorch的基本使用方法。 一、导入库 import numpy as np import matplotlib.pyplot as plt import torch from torch.autograd import Variable # 定义求…...

哪个证券公司可以加杠杆,淘配网是您的杠杆综合网站!
在证券市场中,投资者经常寻求提高资金杠杆以获得更高的回报。杠杆交易可以让您在不必拥有等额本金的情况下,参与更多的交易活动。然而,为了进行杠杆交易,您需要找到一家证券公司或平台,可以为您提供这种服务。本文将介…...

万字解读|怎样激活 TDengine 最高性价比?
不知不觉间,TDengine 已经 6 岁多了。在这 6 年多的时间里,我们从零开始,在一行又一行代码的淬炼下,TDengine 从 1.6 走过 2.0,终于走到如今的 3.0 时代。 自 2022 年下旬发布以来,经过我们不断地打磨优化…...

【目标检测】大图包括标签切分,并转换成txt格式
前言 遥感图像比较大,通常需要切分成小块再进行训练,之前写过一篇关于大图裁切和拼接的文章【目标检测】图像裁剪/标签可视化/图像拼接处理脚本,不过当时的工作流是先将大图切分成小图,再在小图上进行标注,于是就不考…...
gitlab登录出现的Invalid login or password问题
前提 我是在一个项目里创建的gitlab账号,想在别的项目里登录或者官网登录发现怎么都登陆不上 原因 在GitLab中,有两种不同的账号类型:项目账号和个人账号(官网账号)。 项目账号:项目账号是在特定GitLab…...

git本地创建分支并推送到远程
1. 创建本地分支并切换到该分支 比如我创建dev分支。git checkout -b相当于把两条命令git branch 分支名、git checkout分支名合成一条,来实现一条命令新建分支切换分支。 git checkout -b dev 2. 将dev分支推送到远程 -u参数与--set-upstream这一串是一个意思&am…...

手机待办事项app哪个好?
手机是日常很多人随身携带的设备,手机除了拥有通讯功能外,还能帮助大家高效管理日常工作,借助手机上的待办事项提醒APP可以快速地帮助大家规划日常事务,提高工作的效率。 过去,我也曾经在寻找一款能够将工作任务清晰罗…...
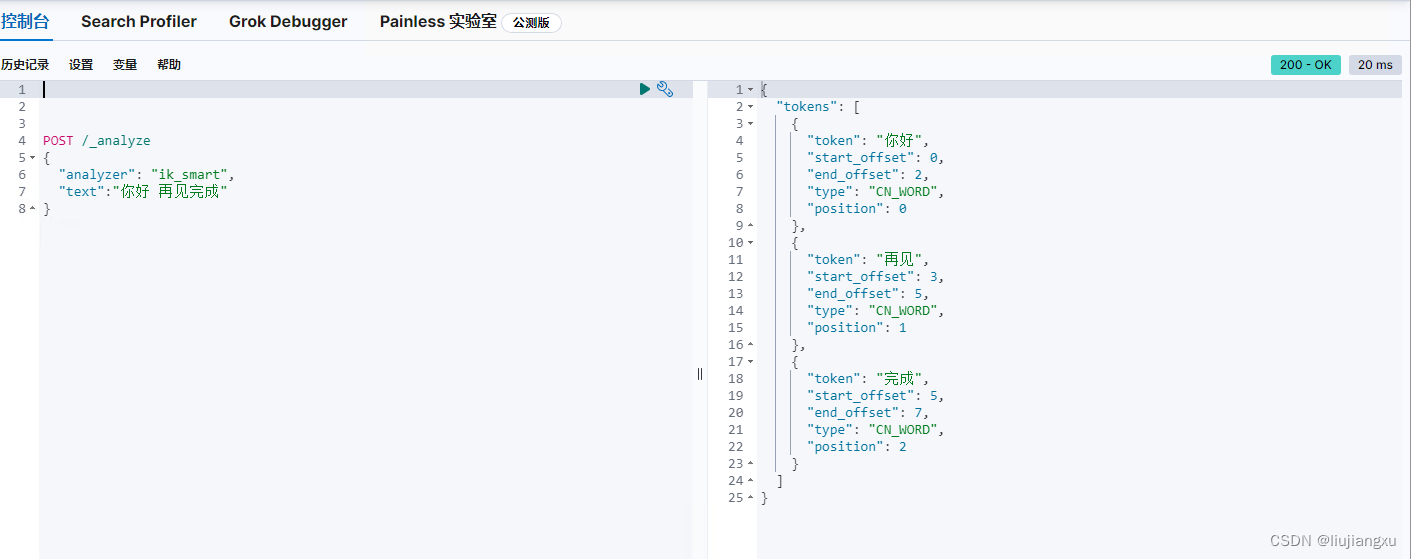
容器运行elasticsearch安装ik分词非root权限安装报错问题
有些应用默认不允许root用户运行,来确保应用的安全性,这也会导致我们使用docker run后一些操作问题,用es安装ik分词器举例(es版本8.9.0,analysis-ik版本8.9.0) 1. 容器启动elasticsearch 如挂载方式&…...

UE4游戏客户端开发进阶学习指南
前言 两年多前写过一篇入门指南,教大家在短时间内快速入门UE4的使用,在知乎被很多人收藏了。如今鸡佬使用UE快三年了,是时候更新一下进阶版本的学习指南。本文对于读者的要求: 有一定的C基础已经入门UE,能够用蓝图和…...

javaee SpringMVC 乱码问题解决
方法一 在web.xml文件中注册过滤器 <!-- 注册过滤器 设置编码 --><filter><filter-name>CharacterEncodingFilter</filter-name><filter-class>org.springframework.web.filter.CharacterEncodingFilter</filter-class><init-param&…...
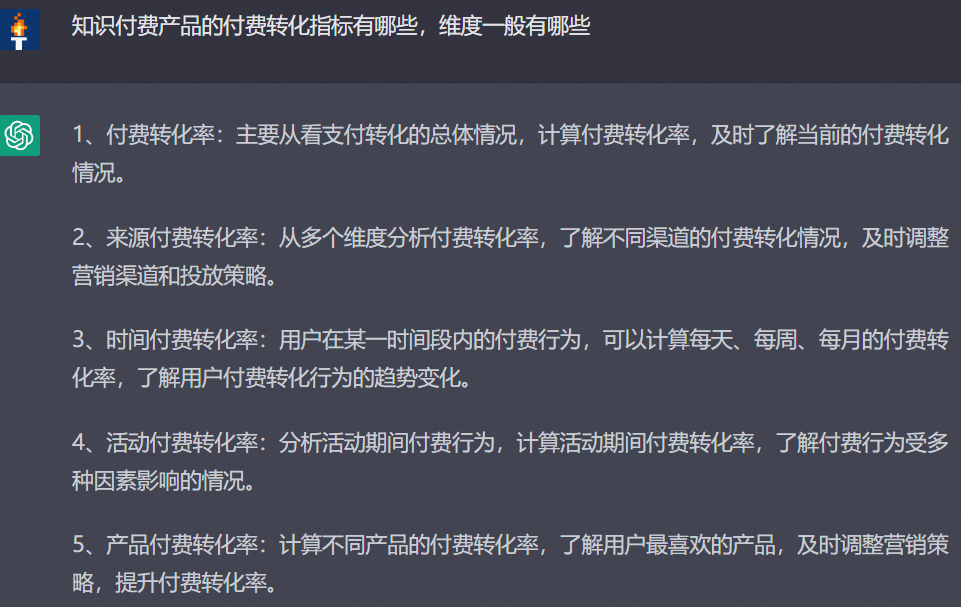
用ChatGPT做数据分析,提升10倍工作效率
目录 写报告分析框架报告框架指标体系设计 Excel 写报告 分析框架 拿到一个专题不知道怎么做?没关系,用ChatGPT列一下框架。 以上分析框架挺像那么回事,如果没思路的话,问问ChatGPT能起到找灵感的作用。 报告框架 报告的框架…...
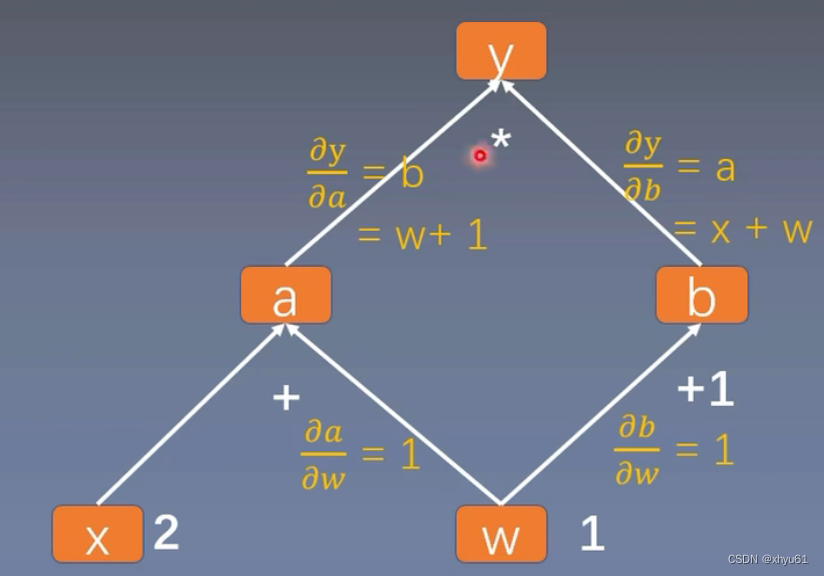
【Pytorch笔记】4.梯度计算
深度之眼官方账号 - 01-04-mp4-计算图与动态图机制 前置知识:计算图 可以参考我的笔记: 【学习笔记】计算机视觉与深度学习(2.全连接神经网络) 计算图 以这棵计算图为例。这个计算图中,叶子节点为x和w。 import torchw torch.tensor([1.]…...
浏览器安装vue调试工具
下载扩展程序文件 下载链接:链接: 下载连接网盘地址, 提取码: 0u46,里面有两个crx,一个适用于vue2,一个适用于vue3,可根据vue版本选择不同的调试工具 crx安装扩展程序不成功,将文件改为rar文件然后解压 安装…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
