数学分析:含参变量的积分
同样很多收敛性的证明不是重点,但里面的知识还是需要适当掌握,知道中间的大致思考和解决路径即可。

 本质还是极限的可交换性,求导可以换到积分里面去操作。
本质还是极限的可交换性,求导可以换到积分里面去操作。
这里要注意变量的区别,首先积分的被积变量是x,但是函数的变量是y,y是参数,所以叫做带参数的积分。

这是一个很有意思的题,首先我们不好求积分的时候,可以先对里面的参变量进行求导。得到一个简单的式子,然后再积分即可。
 这是积分的可交换性。
这是积分的可交换性。

要反常积分收敛,就是说要在无界的部分,积分足够小。
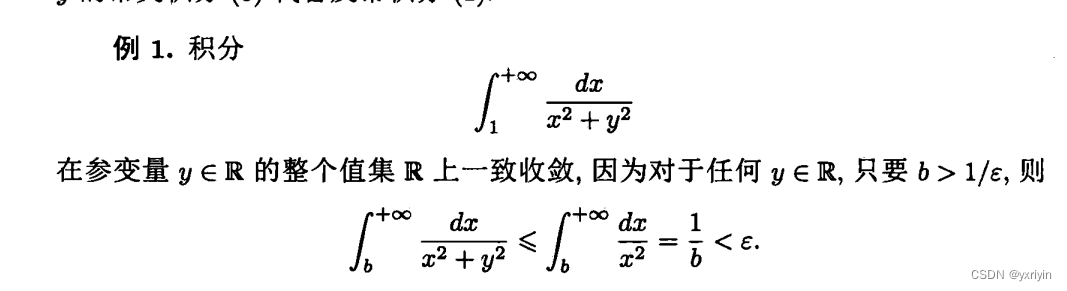 我们要证明在足够大的情况下,这个积分是很小的。
我们要证明在足够大的情况下,这个积分是很小的。



 各种可交换。一般我们认为大部分能列出来的都是可交换的。
各种可交换。一般我们认为大部分能列出来的都是可交换的。

反常积分的技巧真是千奇百怪。


还是各种可交换。





终于开始讲卷积了。物理中的卷积,是针对输入信号f,通过一个仪器的算子A,变成输出信号。如果A是一个平移变算子,也就是时间推移后,依然产生完全一样的信号,只是t不同。
 要根据输入信号来求输出信号。要根据输出信号反推输入信号。一般来说,只要知道仪器对脉冲的响应,就可以知道所有它对其他信号的响应。
要根据输入信号来求输出信号。要根据输出信号反推输入信号。一般来说,只要知道仪器对脉冲的响应,就可以知道所有它对其他信号的响应。

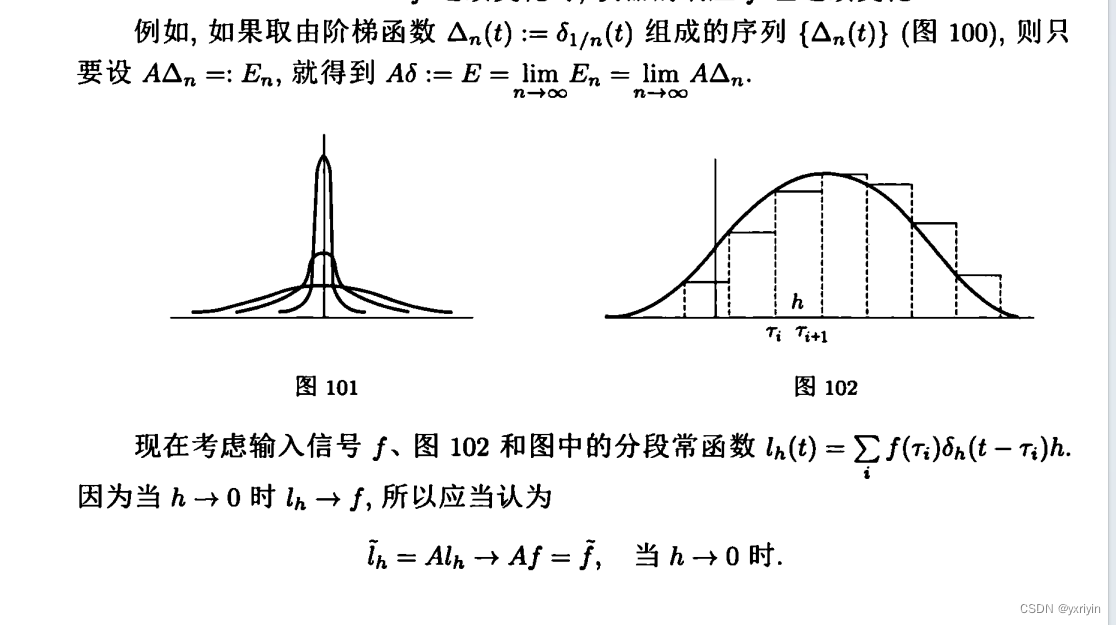
重点来了,我们一个普通的信号f,可以看成分段函数,而当分段趋于无穷的时候,分段函数就趋于f,而这个分段函数,可以用脉冲函数求和来表示。这个真是太秒了。原来是这么理解的。

因为算子是线性的,所以可以把A挪进去。最后我们得到了一个卷积的公式。所以我们第一个问题得到了解决,为什么知道脉冲函数的响应,就能知道所有其他函数的响应。通过卷积即可。而这个卷积很有意思,首先它引入了两个未知变量,其中一个是被积变量,而另一个是参变量。一般,我们可以认为,对于原始函数f(t),我们通过引入了一个脉冲函数,实际也引入了一个额外的时间平移变量。这个引入的时间平移变量,是最终会被积分的。而t本来就是原始函数的变量。

这样,我们就定义了一个更加一般的卷积。
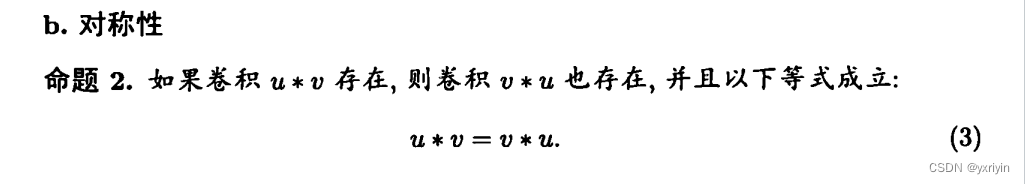

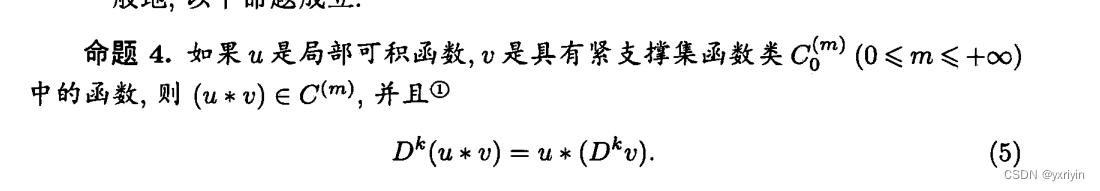
这些都是卷积的重要性质。
 这也是一个很重要的例子,我们一个函数和一个脉冲函数卷积,会取到一个平均的作用。
这也是一个很重要的例子,我们一个函数和一个脉冲函数卷积,会取到一个平均的作用。
显然,如果alpha趋向于0,那么自然这个积分就是f(y)了。因为积分就是面积,面积除以底,那自然就是高了。


 这个的意思是说,一些函数可能不是无限次可微的,那么我们把它和某个 特定的函数卷积后,就可以得到一个无限次可微的函数,而且他是逼近原始函数的。
这个的意思是说,一些函数可能不是无限次可微的,那么我们把它和某个 特定的函数卷积后,就可以得到一个无限次可微的函数,而且他是逼近原始函数的。

这个也很吊,可以用多项式逼近所有区间上的连续函数。
 这里要注意,我们用了卷积,自然就会引入一个新的被积变量,它应该是看成一个常数。
这里要注意,我们用了卷积,自然就会引入一个新的被积变量,它应该是看成一个常数。

所有周期函数都可以用cos sin来逼近。
后面含参变量的重积分也是各种可交换,就不提了。
相关文章:

数学分析:含参变量的积分
同样很多收敛性的证明不是重点,但里面的知识还是需要适当掌握,知道中间的大致思考和解决路径即可。 本质还是极限的可交换性,求导可以换到积分里面去操作。 这里要注意变量的区别,首先积分的被积变量是x,但是函数的变量…...

关于一篇ElementUI之CUD+表单验证
目录 一.CUD增删改查简述 1.1.增删改功能实现 二.表单验证 前端所有代码: 好啦今天就分享到这了,希望能帮到你哦!!! 以下的代码基于我博客中的代码进行续写 : 关于ElementUI之动态树数据表格分页实例 一.CUD增删改…...

VUE模板编译的实现原理
前言 在Vue.js 2.0中,模板编译是通过将模板转换为渲染函数来实现的。渲染函数是一个函数,它返回虚拟DOM节点,用于渲染实际的DOM。Vue.js的模板编译过程可以分为以下几个步骤: 将模板解析为抽象语法树(AST)…...

基础算法之——【动态规划之路径问题】1
今天更新动态规划路径问题1,后续会继续更新其他有关动态规划的问题!动态规划的路径问题,顾名思义,就是和路径相关的问题。当然,我们是从最简单的找路径开始! 动态规划的使用方法: 1.确定状态并…...
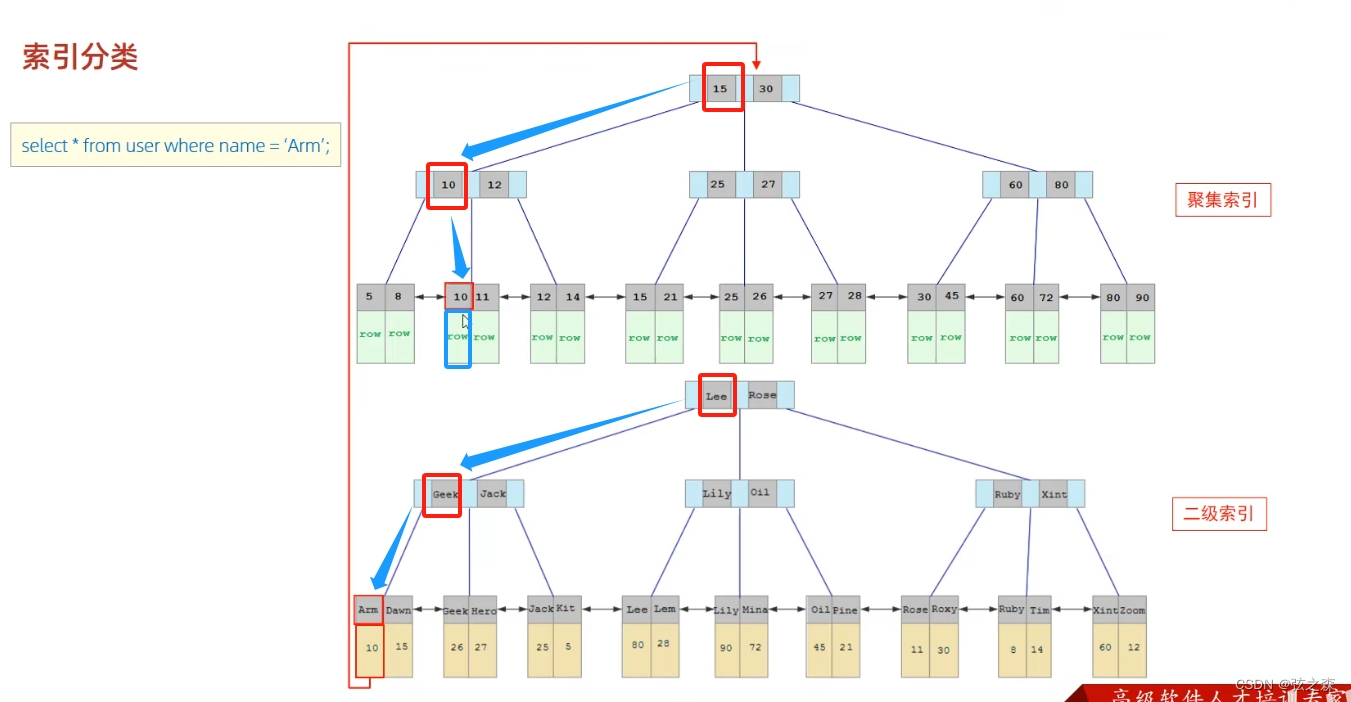
三十三、【进阶】索引的分类
1、索引的分类 (1)总分类 主键索引、唯一索引、常规索引、全文索引 (2)InnoDB存储引擎中的索引分类 2、 索引的选取规则(InnoDB存储引擎) 如果存在主键,主键索引就是聚集索引; 如果不存在主键ÿ…...
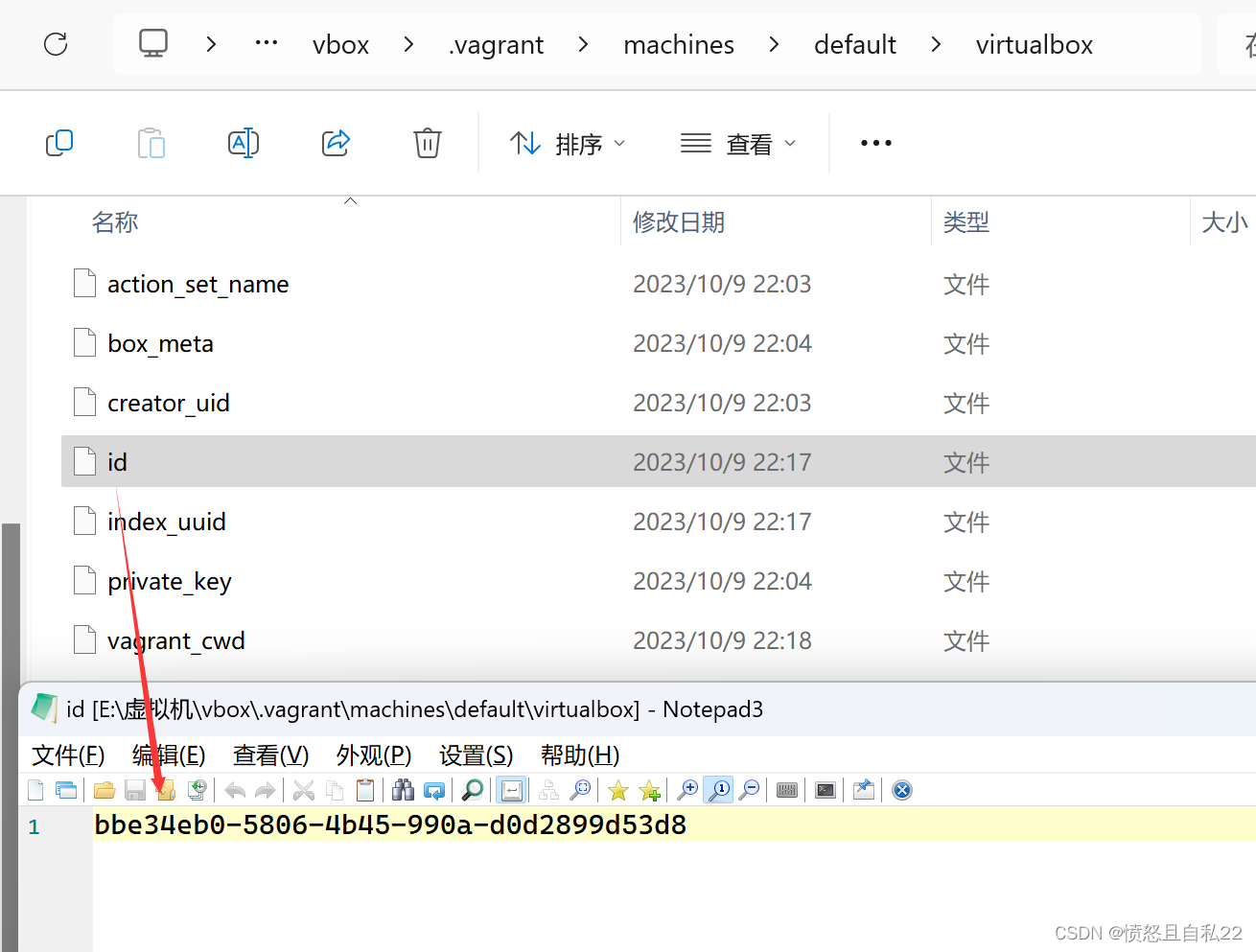
VBox启动失败、Genymotion启动失败、Vagrant迁移
VBox启动失败、Genymotion启动失败、Vagrant迁移 2023.10.9 最新版本vbox7.0.10、Genymotion3.5.0 Vbox启动失败 1、查看日志 Error -610 in supR3HardenedMainInitRuntime! (enmWhat4) Failed to locate ‘vcruntime140.dll’ 日志信息查看方法->找到虚拟机所在位置->…...
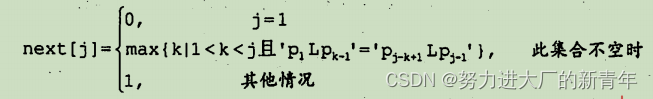
一篇短小精悍的文章让你彻底明白KMP算法中next数组的原理
以后保持每日一更,由于兴趣较多,更新内容不限于数据结构,计算机组成原理,数论,拓扑学......,所谓:深度围绕职业发展,广度围绕兴趣爱好。往下看今日内容 一.什么是KMP算法 KMP&#x…...
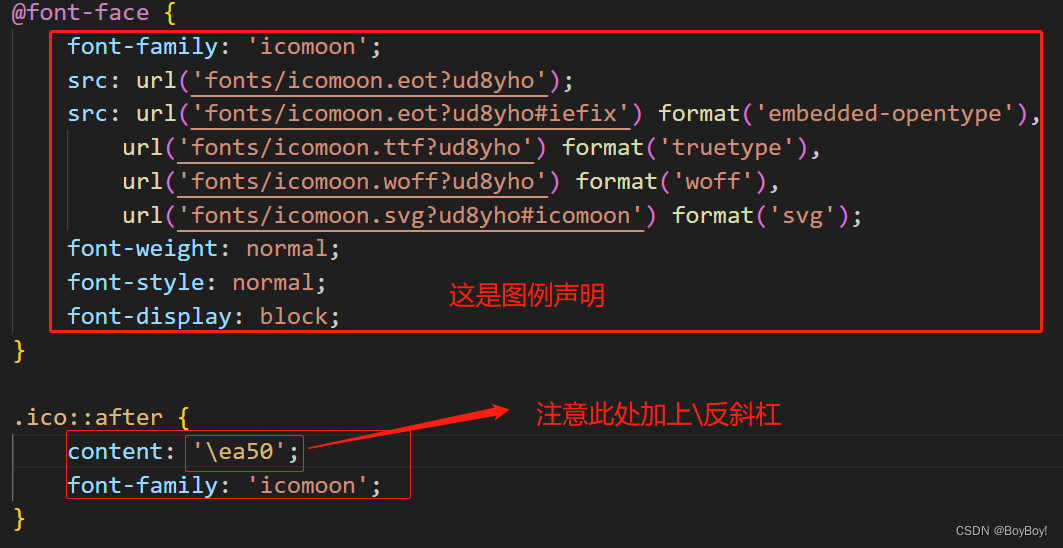
CSS盒子定位的扩张
定位的扩展 绝对定位(固定定位)会完全压住盒子 浮动元素不会压住下面标准流的文字,而绝对定位或固定位会压住下面标准流的所有内容 如果一个盒子既有向左又有向右,则执行左,同理执行上 显示隐藏 display: none&…...
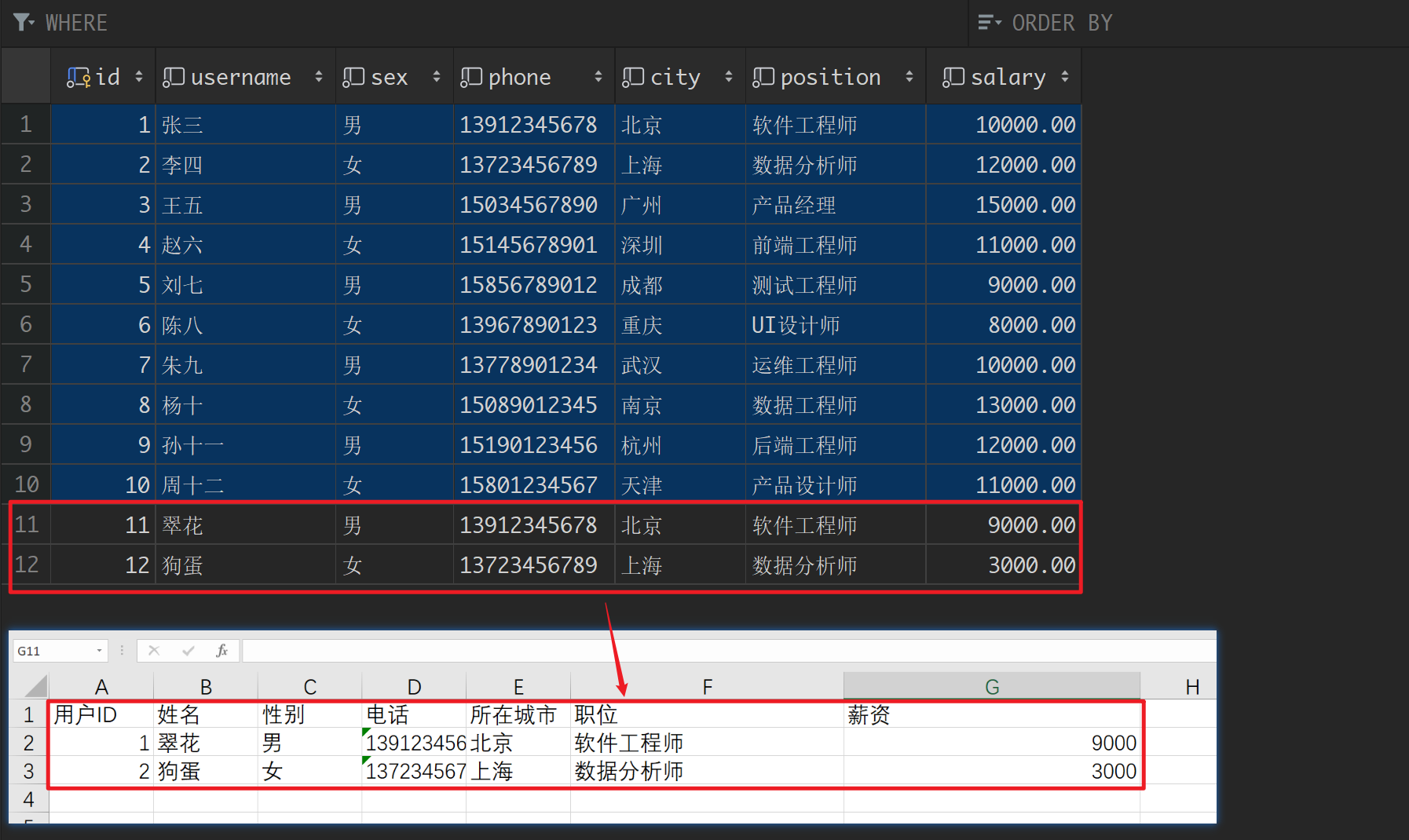
SpringBoot整合POI实现Excel文件读写操作
1.环境准备 1、导入sql脚本: create database if not exists springboot default charset utf8mb4;use springboot;create table if not exists user (id bigint(20) primary key auto_increment comment 主键id,username varchar(255) not null comment 用…...

从零开始的力扣刷题记录-第八十七天
力扣每日四题 129. 求根节点到叶节点数字之和-中等130. 被围绕的区域-中等437. 路径总和 III-中等376. 摆动序列-中等总结 129. 求根节点到叶节点数字之和-中等 题目描述: 给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 …...

【1】c++设计模式——>UML类图的画法
UML介绍 UML:unified modeling language 统一建模语言 面向对象设计主要就是使用UML类图,类图用于描述系统中所包含的类以及他们之间的相互关系,帮助人们简化对系统的理解,他是系统分析和设计阶段的重要产物,也是系统编码和测试的…...

SAP UI5 指定 / 变更版本
SAP UI5 指定 / 变更版本 Currently, SAP Fiori tools support SAP Fiori elements and SAPUI5 freestyle projects with minimum SAPUI5 versions 1.65 or higher. In case there’s a need to test an existing projects with a lower SAPUI5 version, the following worka…...

SpringMVC中异常处理详解
单个控制器异常处理 // 添加ExceptionHandler,表示该方法是处理异常的方法,属性为处理的异常类ExceptionHandler({java.lang.NullPointerException.class,java.lang.ArithmeticException.class})public String exceptionHandle1(Exception ex, Model mo…...
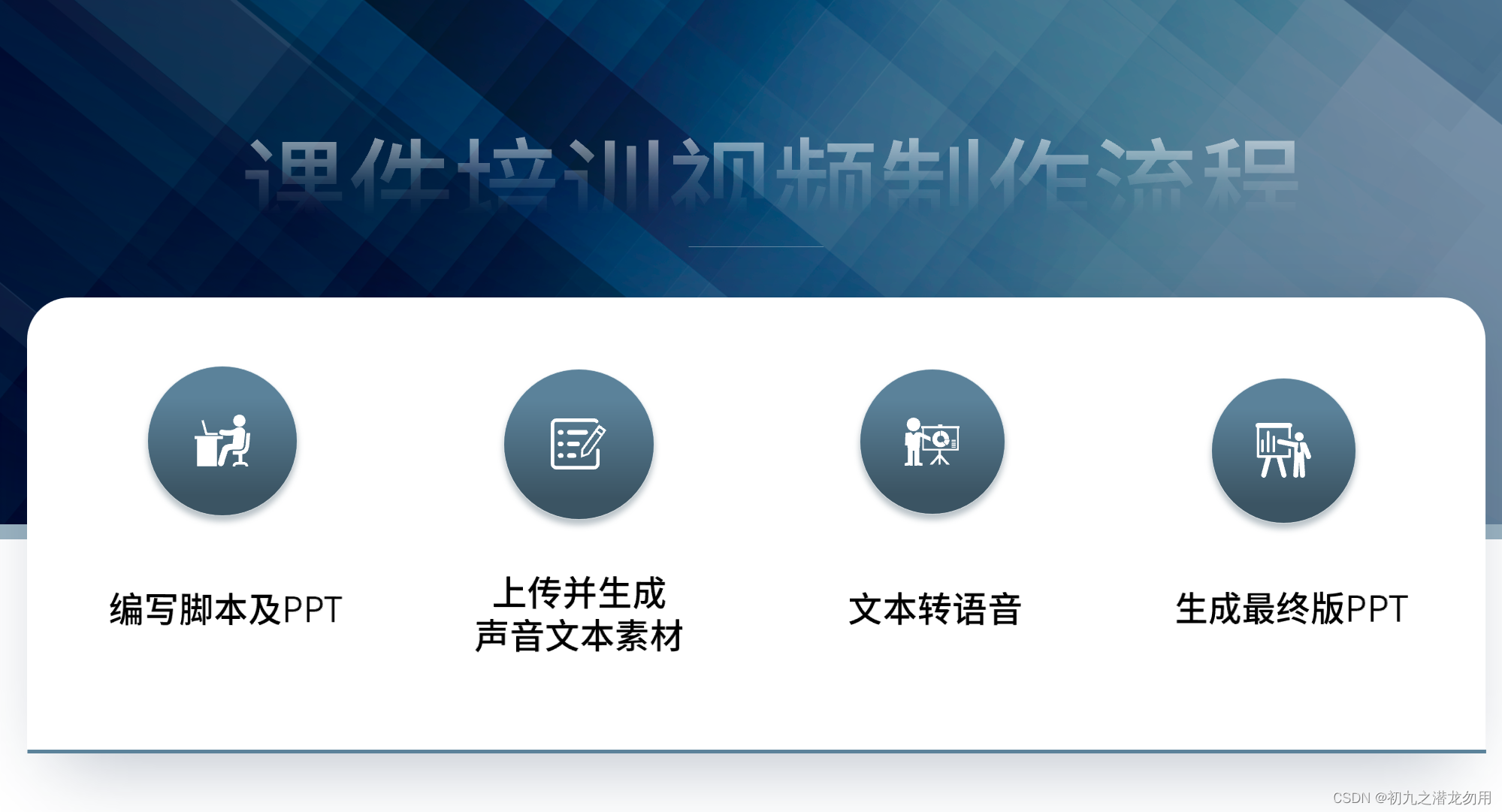
PPT课件培训视频生成系统实现全自动化
前言 困扰全动自化的重要环节,AI语音合成功能,终于可以实现自动化流程,在此要感谢团队不懈的努力和韧性的精神! 实现原理 请参照我的文章《Craneoffice云PPT课件培训视频生成系统》 基本流程 演示视频 PPT全自动 总结 过去实…...
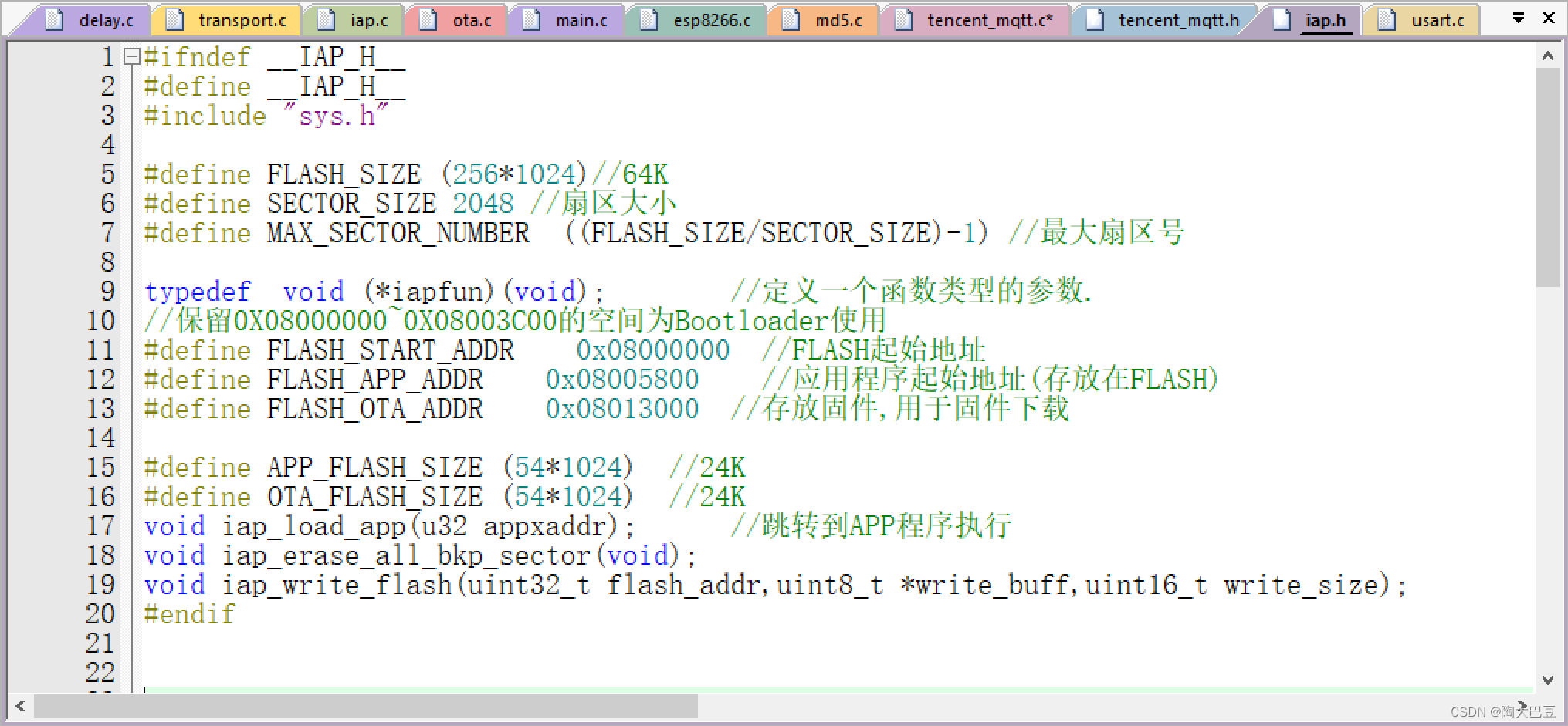
基于腾讯云的OTA远程升级
一、OTA OTA即over the air,是一种远程固件升级技术,它允许在设备已经部署在现场运行时通过网络远程更新其固件或软件。OTA技术有许多优点,比如我们手机系统有个地方做了优化,使用OTA技术我们就不用召回每部手机,直接通过云端就可…...
如何在VS2022中进行调试bug,调试的快捷键,debug与release之间有什么区别
什么是bug 在学习编程的过程中,应该都听说过bug吧,那么bug这个词究竟是怎么来的呢? 其实Bug的本意是“虫子”或者“昆虫”,在1947年9月9日,格蕾丝赫柏,一位为美国海军工作的电脑专家,也是最早…...

初识jmeter及简单使用
目录 1、打开页面: 2、添加线程组: 3、线程组中设置参数: 4、添加请求 5、添加一个http请求后,设置请求内容 6、添加察看结果树 7、执行,查看结果 一般步骤是:在测试计划下面新建一个线程组…...
Spring 在多线程环境下如何确保事务一致性
问题在现 如何解决异步执行 多线程环境下如何确保事务一致性 事务王国回顾 事务实现方式回顾 编程式事务 利用编程式事务解决问题 问题分析完了,那么如何解决问题呢? 小结 问题在现 我先把问题抛出来,大家就明白本文目的在于解决什…...

[Machine Learning] Learning with Noisy Data
文章目录 Probabilistic Perspective of NoiseBias and VarianceRobustness among Surrogate Loss FunctionsNMF Probabilistic Perspective of Noise 假设数据来源于一个确定的函数,叠加了高斯噪声。我们有: y h ( x ) ϵ y h(x) \epsilon yh(x)ϵ…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...