核货宝:服装店收银系统如何选择?收银系统选购指南!
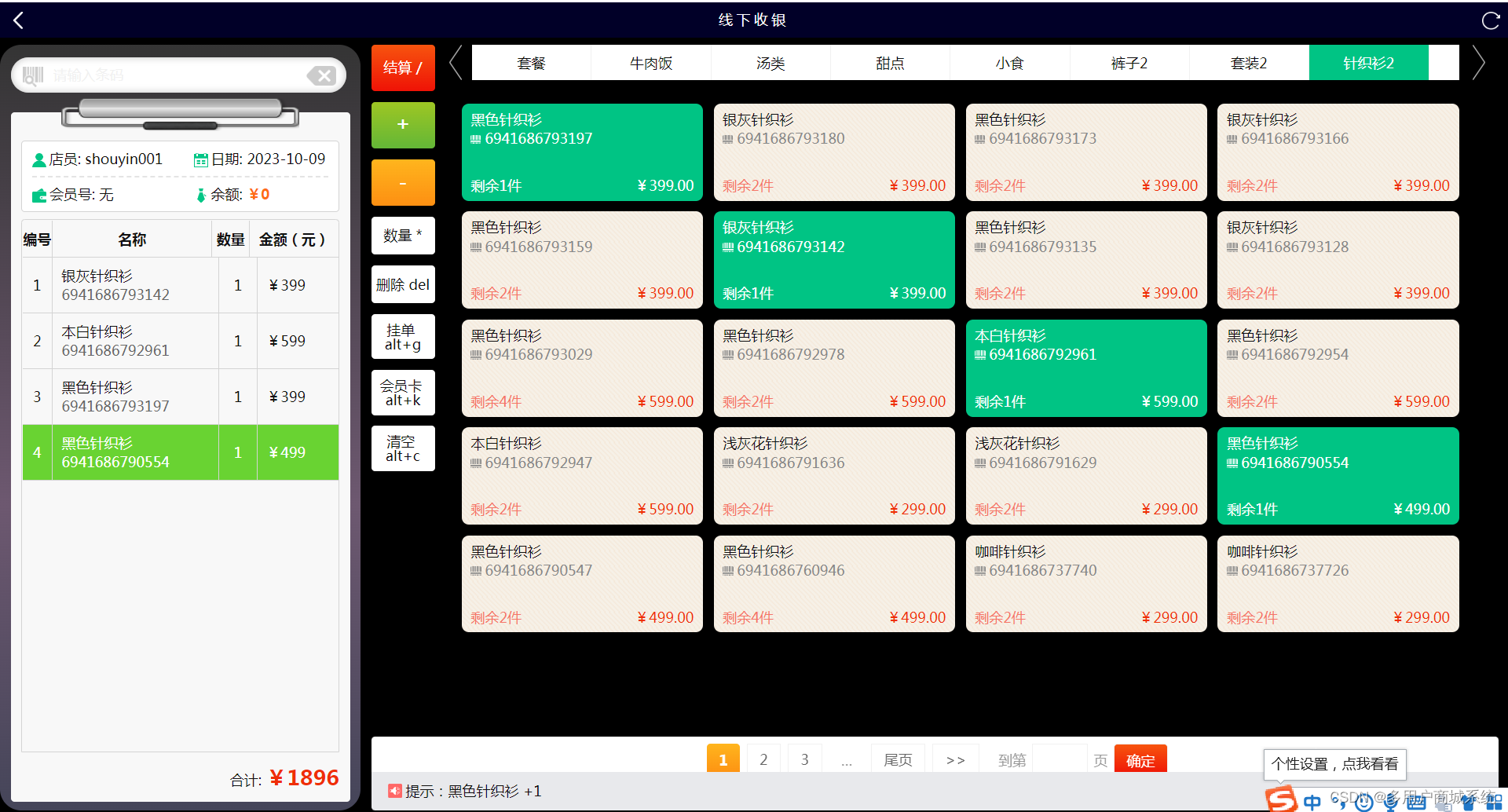
对于各行各业而言,收银系统都是必备的工具。特别是对于像服装店这样的零售门店来说,选择一套适合的收银系统尤为重要。在选择收银系统时,有一些关键的技巧需要注意,以达到软硬件合理搭配、节省开支的目的。下面将分享四个选购服装店收银系统的关键技巧,让我们一起来了解一下吧!
1. 考虑软硬件适配度
首先,一个好的服装店收银系统应该具备软硬件适配度,也就是软件与硬件之间的无缝连接。在软件方面,它应该能够兼容并支持服装店的特殊需求,比如会员管理、库存管理、交易记录等功能。在硬件方面,收银系统应该兼容各种常见设备,比如条码扫描器、小票打印机、收银盒子等。确保软硬件的良好兼容性,将为你提供更顺畅的收银体验。
2. 注意费用清晰合理
其次,在选择收银系统时,费用透明和合理也是需要考虑的因素。了解收银系统的收费模式非常重要。有些系统采用按年收费的方式,你需要定期支付费用以继续使用系统;而有些系统则提供终身买断模式,即一次性购买后,系统将拥有终身使用权。根据服装店的具体情况,选择适合的费用模式,以便更好地控制成本。
3. 确保功能齐全且易于使用
功能齐全且易于使用是一个理想的收银系统应该具备的特点。首先,它应该具备基本的收银功能,比如快速扫码、计算价格等。其次,由于商品经常批量更换,系统还应该支持商品进销存、商品批量导入导出、服装批量改价,促销活动、报表生成等功能。此外,使用界面应该简洁明了,方便操作和培训员工。在选择收银系统时,建议尝试一些免费试用版本,以便评估其功能和易用性。
4. 选择可靠的售后服务团队
最后,考虑收银系统供应商的售后服务可靠性至关重要。一个拥有专业售后团队的供应商将能够及时解决你在使用过程中遇到的问题,并提供技术支持。在选择供应商时,可以咨询其他用户的评价并了解其售后服务覆盖范围。确保能够获得及时有效的支持,将有助于你更好地应对潜在的技术问题。
综上所述,在选购过程中,综合考虑各项因素,选择一套真正适合您服装店需求的收银系统,将帮助你提高工作效率,节省开支,并为顾客提供更好的购物体验。
相关文章:

核货宝:服装店收银系统如何选择?收银系统选购指南!
对于各行各业而言,收银系统都是必备的工具。特别是对于像服装店这样的零售门店来说,选择一套适合的收银系统尤为重要。在选择收银系统时,有一些关键的技巧需要注意,以达到软硬件合理搭配、节省开支的目的。下面将分享四个选购服装…...

GB/T 7134-2008 浇筑型工业有机玻璃板材检测
非改性浇筑PMMA板材是指甲基丙烯酸甲酯均聚物板材,或者甲基丙烯酸甲酯与丙烯酸酯类或甲基丙烯酸酯类单体的共聚物板材,通过适当的引发剂本体聚合生产。 GB/T 7134-2008浇筑型工业有机玻璃板材测试项目: 测试项目 测试方法 拉伸强度 GB/T …...
)
数据采集平台(二)
5. 安装Kafka 5.1 基础架构 为方便扩展,并提高吞吐量,一个topic分为多个partition配合分区的设计,提出消费者组的概念,组内每个消费者并行消费为提高可用性,为每个partition增加若干副本,类似NameNode HA…...

Nginx + PHP 异常排查,open_basedir 异常处理
新上一个网站,通过域名访问失败,排查方法如下: 开启异常日志 开启域名下,nginx的异常日志,并查看日志 tail -f /var/log/nginx/nginx.localhost.error.log开启php的异常日志,该配置位于php.ini文件下 …...
Linux免密登录
目标: 192.168.233.31 ton-pc-003 192.168.233.32 ton-pc-004 在ton-pc-004(以下简称004)免密登录ton-pc-003(以下简称003) 具体流程和说明: 1、在004(客户机)中生成秘钥对 ssh…...

迷宫 蓝桥杯
问题描述 这天, 小明在玩迷宫游戏。 迷宫为一个 nn 的网格图, 小明可以在格子中移动, 左上角为 (1,1), 右下角 (n, n)为终点。迷宫中除了可以向上下左右四个方向移动一格以外, 还有 m 个双向传送门可以使用, 传送门可以连接两个任意格子。 假如小明处在格子(x1,y1), 同时有…...
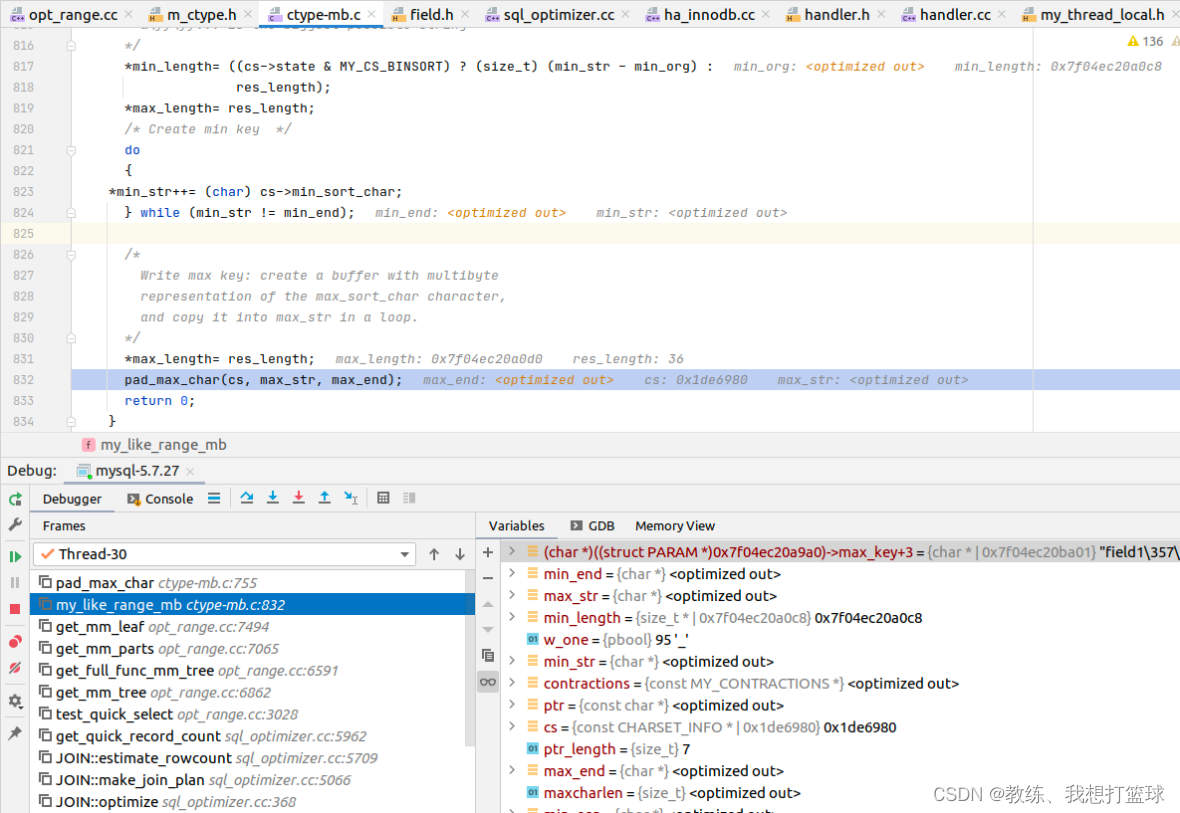
25 mysql like 是否使用索引
前言 这里主要是 探究一下 explain $sql 中各个 type 诸如 const, ref, range, index, all 的查询的影响, 以及一个初步的效率的判断 这里会调试源码来看一下 各个类型的查询 需要 lookUp 的记录 以及 相关的差异 此系列文章建议从 mysql const 查询 开始看 测试表结构…...

Android---Class 对象在执行引擎中的初始化过程
一个 class 文件被加载到内存中的步骤如下图所示: 装载 装载是指 Java 虚拟机查找 .class 文件并生成字节流,然后根据字节流创建 java.lang.Class 对象的过程。 1. ClassLoader 通过一个类的全限定名(包名类名)来查找 .class 文件…...
Altium Designer实用系列(二)----PCB绘图小技巧
一、技巧总结 1.1 丝印大小 在导入PCB之后,元器件的丝印一般都是strock font,个人感觉比较大,也不美观,但是一个个修改成true type又比较麻烦。简便方法是使用相似查找全部修改: 此时会选中所有stroke 类型的丝印ÿ…...
threejs-开发入门与调试设置
近年来web得到了快速的发展。随着HTML5的普及,网页的表现能力越来越强大。网页上已经可以做出很多复杂的动画,精美的效果。还能通过WebGL在网页中绘制高性能的3D图形。 学习资料来源:https://www.three3d.cn/threejs/01-%E5%BC%80%E5%8F%91%E…...
win11安装双系统Ubuntu的坎坷记录
之前一直装的都是在一个硬盘中,这是是两块盘。 我的电脑是惠普暗影精灵8Pro 一 安装前的准备工作 1.1 记得先关闭,Bitlocker 输入wins,搜索框输入:设备加密设置 1.2 BIOS设置 (惠普这电脑是开机时按 F10࿰…...

关于docker的xuexi
概念了解 1.镜像: 类似于类与实例关系中的类,也类似于系统镜像的概念,对于前端而言,镜像就是包含了代码运行所需要的一切产物、依赖、配置等。这样的话,可以保证每次程序运行的环境一致。构建镜像,一般都…...

Python接口自动化测试实战详解,你想要的全都有
前言 接口自动化测试是当前软件开发中最重要的环节之一,可以提高代码质量、加速开发周期、减少手工测试成本等优点。Python语言在接口自动化测试方面应用广泛,因为它具有简单易学、开发效率高、库丰富等特点。 一、接口自动化测试概述 接口自动化测试…...

SparkSQL 外部数据源
1.简介 1.1 多数据源支持 Spark 支持以下六个核心数据源,同时 Spark 社区还提供了多达上百种数据源的读取方式,能够满足绝大部分使用场景。 - CSV - JSON - Parquet - ORC - JDBC/ODBC connections - Plain-text files 1.2 读数据格式 所有读取 API 遵循以下调用格式: // …...

leetcode做题笔记167. 两数之和 II - 输入有序数组
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 < index1 < index2 < numbers…...

[ZJCTF 2019]NiZhuanSiWei - 伪协议+文件包含+反序列化
[ZJCTF 2019]NiZhuanSiWei 1 解题流程1.1 分析1.2 解题 题目源码: <?php $text $_GET["text"]; $file $_GET["file"]; $password $_GET["password"]; if(isset($text)&&(file_get_contents($text,r)"welcome t…...
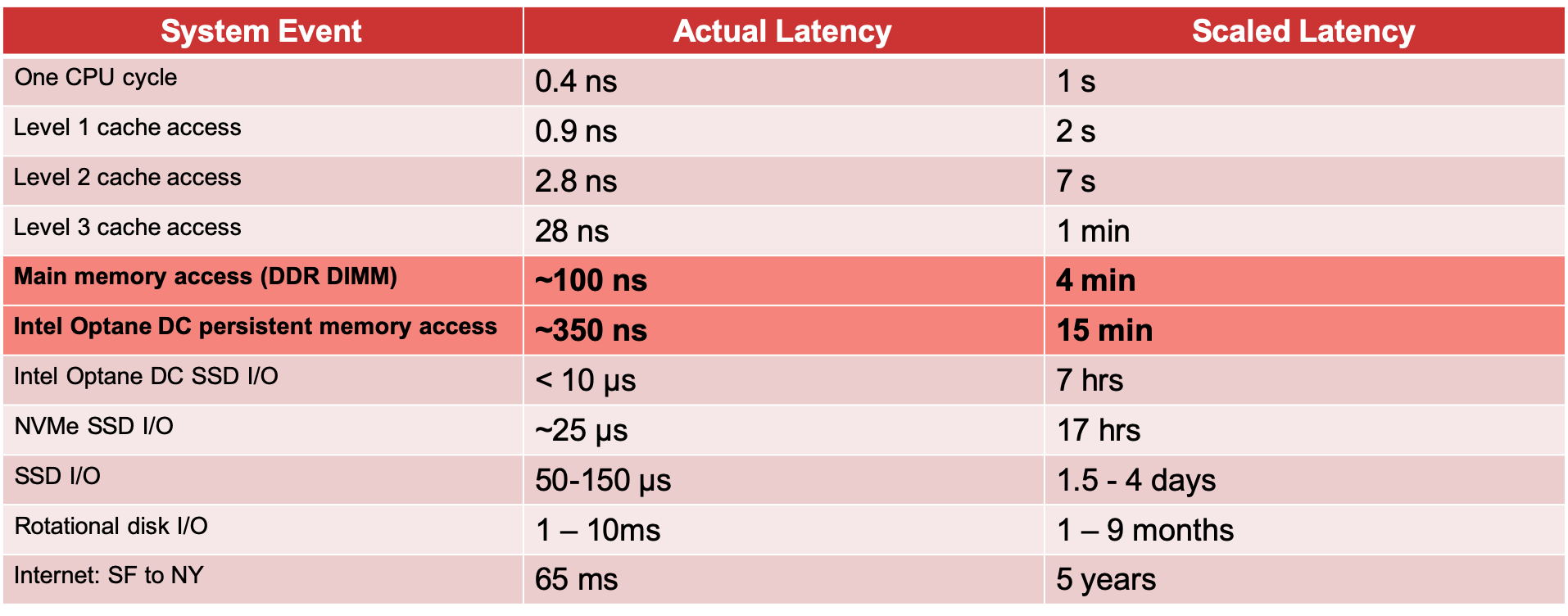
如何提升和扩展 PostgreSQL — 从共享缓冲区到内存数据网格
利用共享缓存和操作系统缓存利用 RAM Postgres 是一个基于磁盘的数据库,即使您的整个架构是围绕磁盘访问设计的,利用 RAM 也很重要。如果按照人类规模的延迟来判断,这可以将延迟从几天缩短到几分钟(图 1)。只需看一下…...
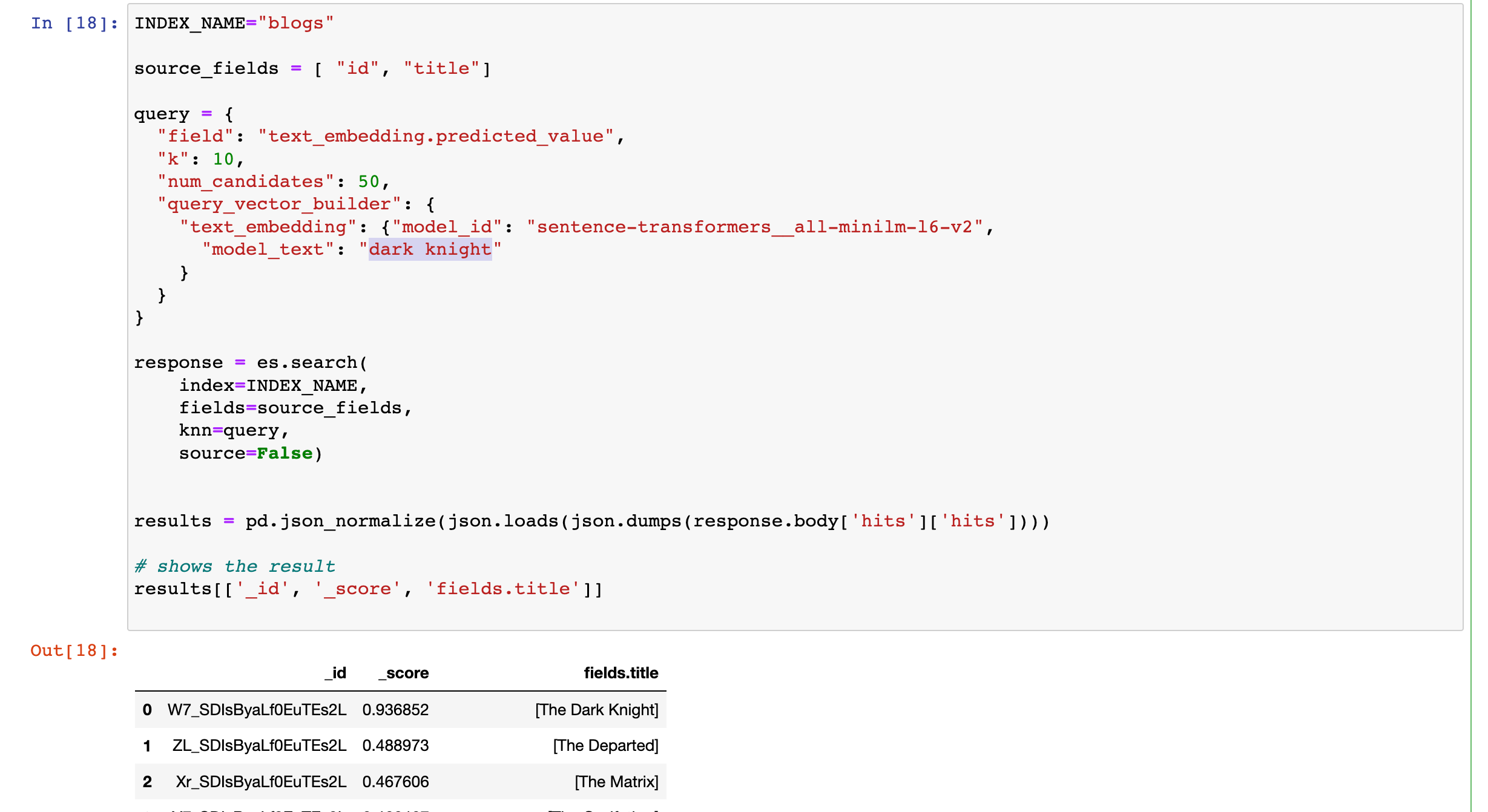
Elasticsearch:使用 huggingface 模型的 NLP 文本搜索
本博文使用由 Elastic 博客 title 组成的简单数据集在 Elasticsearch 中实现 NLP 文本搜索。你将为博客文档建立索引,并使用摄取管道生成文本嵌入。 通过使用 NLP 模型,你将使用自然语言在博客文档上查询文档。 安装 Elasticsearch 及 Kibana 如果你还没…...
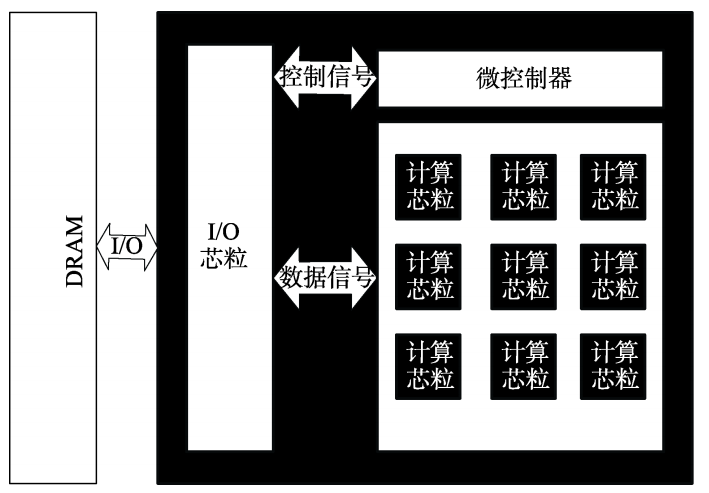
论文解析——异构多芯粒神经网络加速器
作者 朱郭益, 马胜,张春元, 王波(国防科技大学计算机学院) 摘要 随着神经网络技术的快速发展, 出于安全性等方面考虑, 大量边缘计算设备被应用于智能计算领域。首先,设计了可应用于边缘计算的异构多芯粒神经网络加速器其基本结构…...
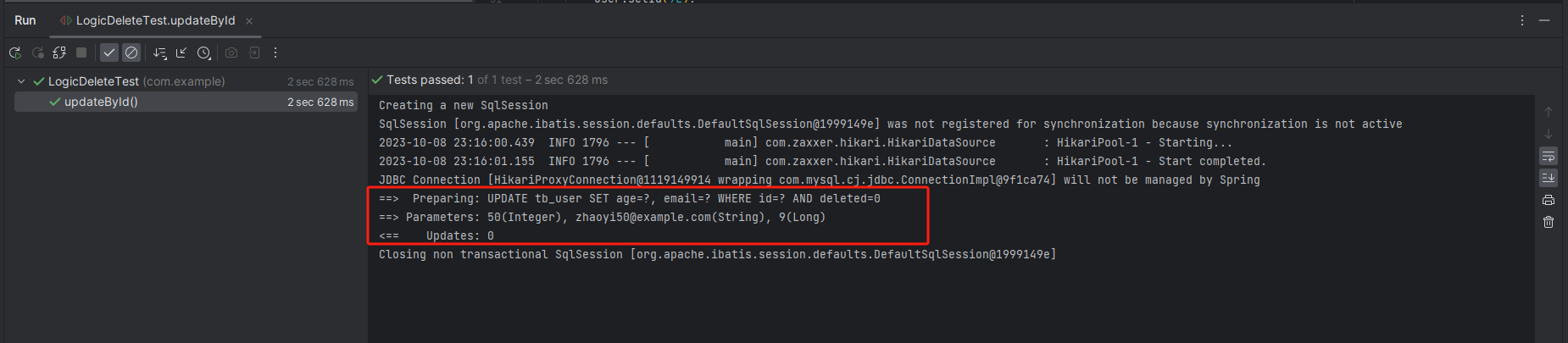
MyBatisPlus(十六)逻辑删除
说明 实际生产中的数据,一般不采用物理删除,而采用逻辑删除,也就是将一条记录的状态改为已删除。 逻辑删除,本质上是更新操作。 MyBatis Plus 框架,提供了逻辑删除功能。在配置了逻辑删除后,增删改查和统…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...
