三数之和[中等]
优质博文:IT-BLOG-CN
一、题目
给你一个整数数组nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i != j、i != k且j != k,同时还满足nums[i] + nums[j] + nums[k] == 0。请你返回所有和为0且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0
不同的三元组是[-1,0,1]和[-1,-1,2]
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为0
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为0
3 <= nums.length <= 3000
-105 <= nums[i] <= 105
二、代码
排序 + 双指针: 题目中要求找到所有「不重复」且和为0的三元组,这个「不重复」的要求使得我们无法简单地使用三重循环枚举所有的三元组。这是因为在最坏的情况下,数组中的元素全部为0,即[0,0,0,0,0]任意一个三元组的和都为0。如果我们直接使用三重循环枚举三元组,会得到O(N3)个满足题目要求的三元组(其中N是数组的长度)时间复杂度至少为O(N3)。在这之后,我们还需要使用哈希表进行去重操作,得到不包含重复三元组的最终答案,又消耗了大量的空间。这个做法的时间复杂度和空间复杂度都很高,因此我们要换一种思路来考虑这个问题。
「不重复」的本质是什么?我们保持三重循环的大框架不变,只需要保证:第二重循环枚举到的元素不小于当前第一重循环枚举到的元素;第三重循环枚举到的元素不小于当前第二重循环枚举到的元素。
也就是说,我们枚举的三元组(a,b,c)满足a≤b≤ca,保证了只有(a,b,c)这个顺序会被枚举到,而(b,a,c)(c,b,a)等等这些不会,这样就减少了重复。要实现这一点,我们可以将数组中的元素从小到大进行排序,随后使用普通的三重循环就可以满足上面的要求。同时,对于每一重循环而言,相邻两次枚举的元素不能相同,否则也会造成重复。举个例子,如果排完序的数组为[]1,2,2,2,4]
nums.sort()
for first = 0 .. n-1// 只有和上一次枚举的元素不相同,我们才会进行枚举if first == 0 or nums[first] != nums[first-1] thenfor second = first+1 .. n-1if second == first+1 or nums[second] != nums[second-1] thenfor third = second+1 .. n-1if third == second+1 or nums[third] != nums[third-1] then// 判断是否有 a+b+c==0check(first, second, third)
这种方法的时间复杂度仍然为O(N3),毕竟我们还是没有跳出三重循环的大框架。然而它是很容易继续优化的,可以发现,如果我们固定了前两重循环枚举到的元素a和b,那么只有唯一的c满足a+b+c=0。当第二重循环往后枚举一个元素b时,由于b′>b,那么满足a+b′+c′=0的c′一定有c′<c,即c′在数组中一定出现在c的左侧。也就是说,我们可以从小到大枚举b,同时从大到小枚举c,即第二重循环和第三重循环实际上是并列的关系。
有了这样的发现,我们就可以保持第二重循环不变,而将第三重循环变成一个从数组最右端开始向左移动的指针,从而得到下面的伪代码:
nums.sort()
for first = 0 .. n-1if first == 0 or nums[first] != nums[first-1] then// 第三重循环对应的指针third = n-1for second = first+1 .. n-1if second == first+1 or nums[second] != nums[second-1] then// 向左移动指针,直到 a+b+c 不大于 0while nums[first]+nums[second]+nums[third] > 0third = third-1// 判断是否有 a+b+c==0check(first, second, third)
这个方法就是我们常说的「双指针」,当我们需要枚举数组中的两个元素时,如果我们发现随着第一个元素的递增,第二个元素是递减的,那么就可以使用双指针的方法,将枚举的时间复杂度从O(N2)减少至O(N)。为什么是O(N)呢?这是因为在枚举的过程每一步中,「左指针」会向右移动一个位置(也就是题目中的b),而「右指针」会向左移动若干个位置,这个与数组的元素有关,但我们知道它一共会移动的位置数为O(N),均摊下来,每次也向左移动一个位置,因此时间复杂度为O(N)。
注意到我们的伪代码中还有第一重循环,时间复杂度为O(N),因此枚举的总时间复杂度为O(N2)。由于排序的时间复杂度为O(NlogN),在渐进意义下小于前者,因此算法的总时间复杂度为O(N2)。
上述的伪代码中还有一些细节需要补充,例如我们需要保持左指针一直在右指针的左侧(即满足b≤c),具体可以参考下面的代码,均给出了详细的注释。
class Solution {public List<List<Integer>> threeSum(int[] nums) {//思想:1、先对 nums 进行排序// 2、先确定第一层循环,通过 0 - nums[x] 得到第二层和第三层的和// 3、将第二层和第三层汇总为一层,left = i + 1; right = nums.length - 1; 进行双指针移动,计算和,如果相等,加入队列,并继续移动指针,直到不满足 left < rightint left = 0, right = 0, size = 0;List<List<Integer>> res = new ArrayList();Arrays.sort(nums);for(int i = 0; i < nums.length; i++) {if (i > 0 && i < nums.length && nums[i] == nums[i-1]) {continue;}// i 发生变化之后,left 和 right 指针都需要发生变化。 第一次将right定义再外部,导致bugleft = i + 1;right = nums.length - 1;int tar = -nums[i];while(left < right) {if (nums[left] + nums[right] == tar) {List<Integer> temp = Arrays.asList(nums[i], nums[left], nums[right]);res.add(temp);// 数据去重while(left < right && nums[left] == nums[left + 1]) {++left;}while(right > left && nums[right] == nums[right - 1]) {--right;}++left;--right;} else if(nums[left] + nums[right] < tar){++left;} else {--right;}}}return res;}
}
时间复杂度: O(N2)其中N是数组nums的长度。
时间复杂度: O(N2),其中N是数组nums的长度。
相关文章:

三数之和[中等]
优质博文:IT-BLOG-CN 一、题目 给你一个整数数组nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i ! j、i ! k且j ! k,同时还满足nums[i] nums[j] nums[k] 0。请你返回所有和为0且不重复的三元组。 注意:答案中不可以…...

基于天牛须优化的BP神经网络(分类应用) - 附代码
基于天牛须优化的BP神经网络(分类应用) - 附代码 文章目录 基于天牛须优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.天牛须优化BP神经网络3.1 BP神经网络参数设置3.2 天牛须算法应用 4.测试结果&#x…...

渗透波菜网站
免责声明 本文发布的工具和脚本,仅用作测试和学习研究,禁止用于商业用途,不能保证其合法性,准确性,完整性和有效性,请根据情况自行判断。如果任何单位或个人认为该项目的脚本可能涉嫌侵犯其权利,…...

Spring Boot:Dao层-实例介绍
目录 Dao层的作用Dao层的特点与 Service 层和 Controller 层的关系实例介绍MenuDaoOperatorLogDaoRoleDaoUserDao四个文件的共同点引用的包使用Repository注解继承JpaRepository接口接口的实体类的主键类型使用 Query()注解 Dao层的作用 负责与数据库进行交互,主要…...

接口测试入门:深入理解接口测试!
很多人会谈论接口测试。到底什么是接口测试?如何进行接口测试?这篇文章会帮到你。 一、前端和后端 在谈论接口测试之前,让我们先明确前端和后端这两个概念。 前端是我们在网页或移动应用程序中看到的页面,它由 HTML 和 CSS 编写…...
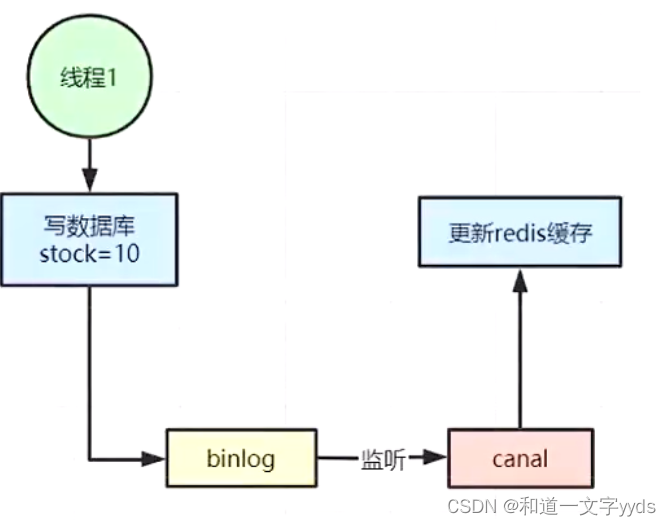
Redis微服务架构
Redis微服务架构 缓存设计 缓存穿透 缓存穿透是指查询一个根本不存在的数据,缓存层和存储层都不会命中,通常出于容错的考虑,如果从存储层查不到数据则不写入缓层。 缓存穿透将导致不存在的数据每次请求都要到存储层去查询,失去…...

【C++】 局部对象,引用返回
1、new 关键字 会在堆内申请空间,如果仅仅是普通调用构造函数,不会在堆内开辟空间。 2、函数调用会形成栈帧,进行压栈操作,函数调用结束,会进行弹栈。 函数内的局部对象,会随着弹栈,而被销毁(…...

线性代数中涉及到的matlab命令-第二章:矩阵及其运算
目录 1,矩阵定义 2,矩阵的运算 3,方阵的行列式和伴随矩阵 4,矩阵的逆 5,克莱默法则 6,矩阵分块 1,矩阵定义 矩阵与行列式的区别: (1)形式上行列式…...

计算机毕业设计选什么题目好?springboot 美食推荐系统
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...
爆肝整理,Jmeter接口性能测试-跨线程调用变量实操(超详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、Jmeter中线程运…...
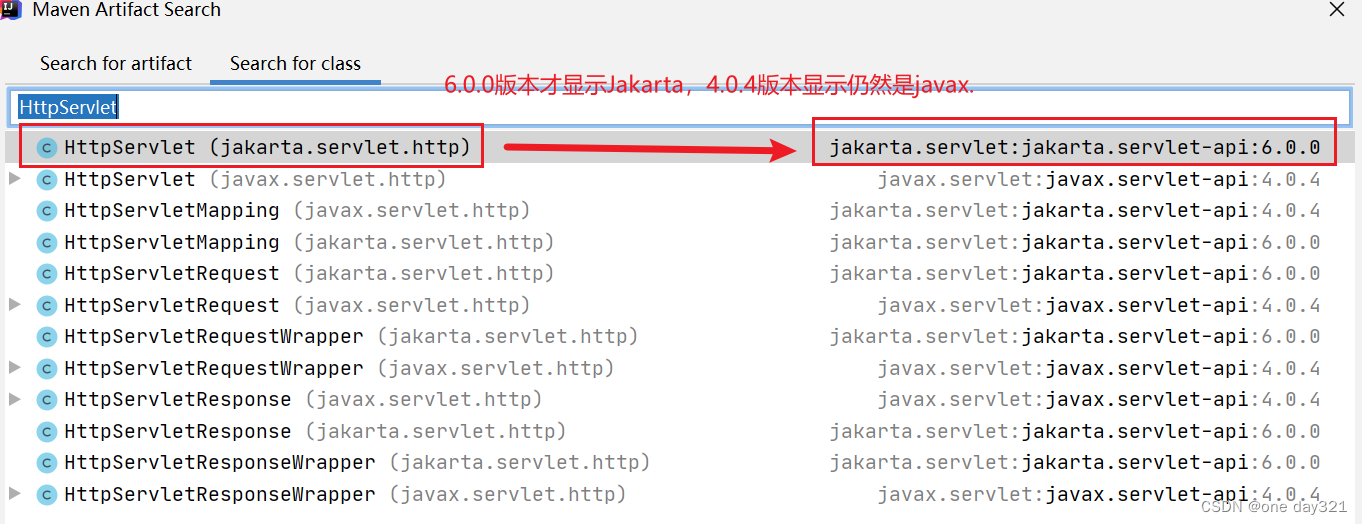
Maven导入程序包jakarta.servlet,但显示不存在
使用前提:(Tomcat10版本)已知tomcat10版本之后,使用jakart.servlet。而tomcat9以及之前使用javax.servlet。 问题描述:在maven仓库有导入了Jakarta程序包,但是界面仍然显示是javax。(下图&…...
es6(二)——常用es6说明
ES6的系列文章目录 es6(一)——var和let和const的区别 文章目录 ES6的系列文章目录一、变量的结构赋值1.数组的结构赋值2.对象的结构赋值 二、模板字符串三、扩展运算符1.字符串的使用2.数组的使用 四、箭头函数1.普通函数的定义2.箭头函数的定义3.箭头…...
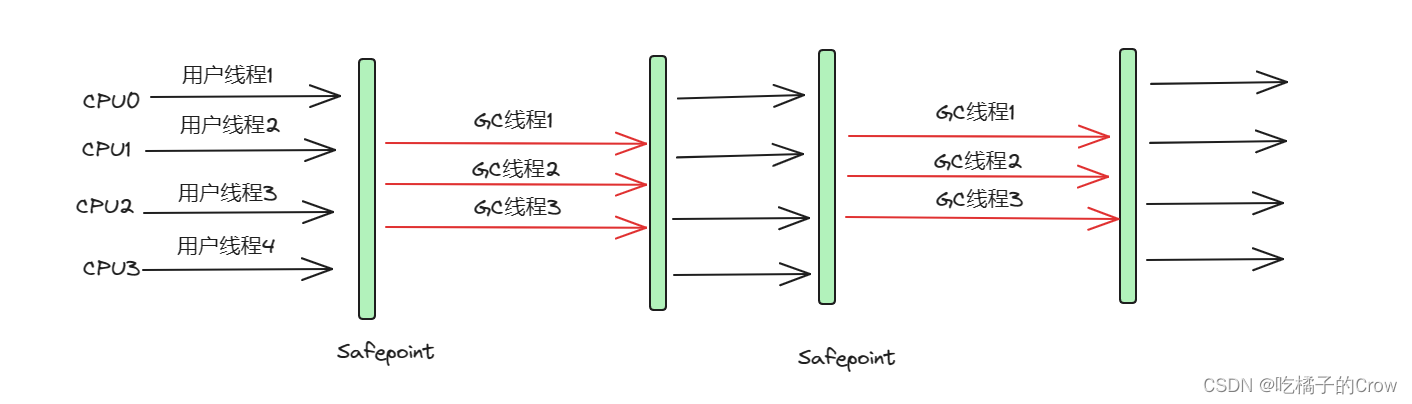
经典垃圾回收器
1.各垃圾回收器之间的配合使用关系 2.垃圾回收器的种类 2.1 Serial收集器(默认新生代收集器) Serial收集器是历史最悠久的收集器,曾经是新生代收集器的唯一选择,它是一个单线程工作的收集器,其“单线程”的意义不仅仅…...

台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法
台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法 台达触摸屏(B07S410)在上载程序时(显示No response from HMI)我以前的电脑是WIN7的,从来没出现过这样的问题,现在换成win10的,怎么都不行,(USB显示是一个大容量存储)换一台电脑(win10)有些行,有些不行…...

[资源推荐] 复旦大学张奇老师科研分享
刷B站的时候首页给我推了这个:【直播回放】复旦大学张奇教授亲授:人工智能领域顶会论文的发表指南先前也散漫地读了些许论文,但没有在一些宏观的方法论下去训练,读的时候能感觉出一些科研的套路,论文写作的套路&#x…...

C++数位动态规划算法:统计整数数目
题目 给你两个数字字符串 num1 和 num2 ,以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件,我们称它是一个好整数: num1 < x < num2 min_sum < digit_sum(x) < max_sum. 请你返回好整数的数目。答案可能很大&…...

ip 网段设置 --chatGPT
问:host all all 127.0.0.1/32 scram-sha-256 里的 127.0.0.1/32 是什么含义 ,要指定某个呢 gpt: 在 PostgreSQL 的 pg_hba.conf 文件中,127.0.0.1/32 是一个用于定义访问控制规则的CIDR(无类域间路由)标记࿰…...

使用JMeter进行接口测试教程
安装 使用JMeter的前提需要安装JDK,需要JDK1.7以上版本目前在用的是JMeter5.2版本,大家可自行下载解压使用 运行 进入解压路径如E: \apache-jmeter-5.2\bin,双击jmeter.bat启动运行 启动后默认为英文版本,可通过Options – Cho…...

文本生成解码策略
解码策略 1. sample实现了怎样的功能 不是直接选择概率最大的token,而是根据多项式分布进行采样获得下一个token 这里的概率通过设置一些策略,进行处理。例如,解码最小长度(当长度小于该值的时候,eos的采样概率为0&am…...
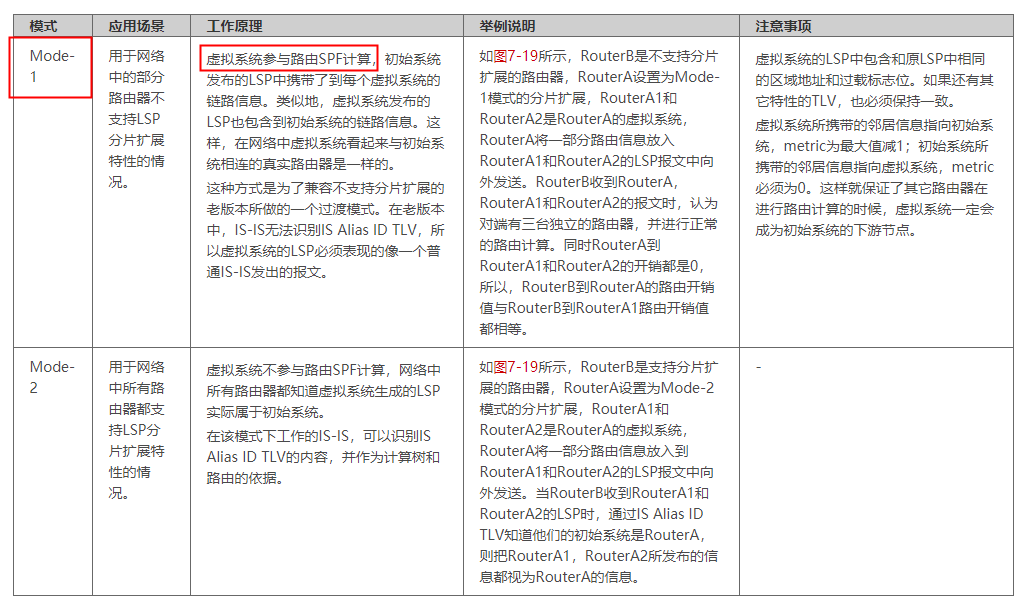
华为数通方向HCIP-DataCom H12-831题库(单选题:221-240)
第221题 以下关于IS-IS的LSP分片功能的描述,正确的是哪一项? A、IS-IS的分片扩展功能的Mode-1模式,虚拟系统是需要参与路由SPF计算的 B、IS-IS的LSP分片功能,是用于让收到LSP分片报文的设备老化相关路由信息 C、IS-IS的分片扩展功能,是通过LSP报文中的LSPID实现的 D、IS-…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
