排序算法-快速排序法(QuickSort)
排序算法-快速排序法(QuickSort)
1、说明
快速排序法是由C.A.R.Hoare提出来的。快速排序法又称分割交换排序法,是目前公认的最佳排序法,也是使用分而治之(Divide and Conquer)的方式,会先在数据中找到一个虚拟的中间值,并按此中间值将所有打算排序的数据分为两部分。其中小于中间值的数据放在左边,而大于中间值的数据放在右边,再以同样的方式分别处理左右两边的数据,直到排序完为止。操作与分割步骤如下:
假设有n项记录,其键值为
。
- 先假设K的值为第一个键值。
- 从左向右找出键值
,使得
。
- 从左向右找出键值
,使得
。
- 如果
,那么
与
互换,并回到步骤2。
- 如果
,那么将
与
互相,并以
为基准点分割成左、右两部分,然后针对左、右两边执行步骤1~5,直到左边键值等于右边键值为止。
2、算法分析
- 在最好情况和平均情况下,时间复杂度为
。在最坏情况下就是每次挑中的中间值不是最大就是最小的,其时间复杂度为
。
- 快速排序法不是稳定排序法。
- 在最坏情况下,空间复杂度为
,而在最好情况下,空间复杂度为
。
- 快速排序法是平均运行时间最快的排序法。
3、C++代码
#include<iostream>
using namespace std;void Print(int tempData[], int tempSize) {for (int i = 0; i < tempSize; i++) {cout << tempData[i] << " ";}cout << endl;
}void Quick(int tempData[], int tempLeft, int tempRight) {int temp;int leftIndex;int rightIndex;int t;if (tempLeft < tempRight) {leftIndex = tempLeft + 1;rightIndex = tempRight;while (true) {for (int i = tempLeft + 1; i < tempRight; i++) {if (tempData[i] >= tempData[tempLeft]) {leftIndex = i;break;}leftIndex++;}for (int j = tempRight; j > tempLeft + 1; j--) {if (tempData[j] <= tempData[tempLeft]) {rightIndex = j;break;}rightIndex--;}if (leftIndex < rightIndex) {temp = tempData[leftIndex];tempData[leftIndex] = tempData[rightIndex];tempData[rightIndex] = temp;}else {break;}}if (leftIndex >= rightIndex) {temp = tempData[tempLeft];tempData[tempLeft] = tempData[rightIndex];tempData[rightIndex] = temp;Quick(tempData, tempLeft, rightIndex - 1);Quick(tempData, rightIndex + 1, tempRight);}}
}int main() {const int size = 10;int data[100] = { 32,5,24,55,40,81,17,48,25,71 };//32 5 24 55 40 81 17 48 25 71//32 5 24 25 40 81 17 48 55 71//32 5 24 25 17 81 40 48 55 71//17 5 24 25 32 81 40 48 55 71//5 17 24 25 32 81 40 48 55 71//5 17 25 24 32 81 40 48 55 71//5 17 25 24 32 71 40 48 55 81//5 17 25 24 32 55 40 48 71 81//5 17 25 24 32 48 40 55 71 81//5 17 25 24 32 40 48 55 71 81Print(data, size);Quick(data, 0, size - 1);Print(data, size);return 0;
}输出结果

相关文章:

排序算法-快速排序法(QuickSort)
排序算法-快速排序法(QuickSort) 1、说明 快速排序法是由C.A.R.Hoare提出来的。快速排序法又称分割交换排序法,是目前公认的最佳排序法,也是使用分而治之(Divide and Conquer)的方式,会先在数…...
Python 简介
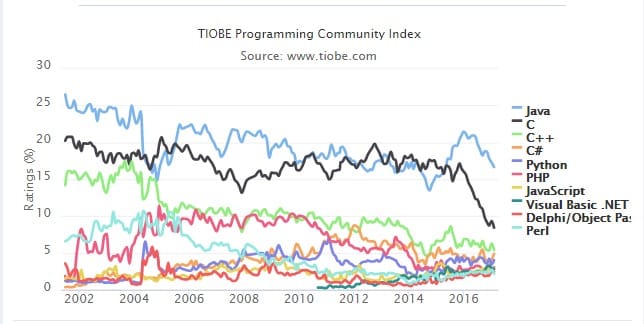
一、Python 简介 Python 是著名的“龟叔” Guido van Rossum 在 1989 年圣诞节期间,为了打发无聊的圣诞节而编写的一个编程语言。牛人就是牛人,为了打发无聊时间竟然写了一个这么牛皮的编程语言。 现在,全世界差不多有 600 多种编程语言&am…...
grafana api创建dashboard 记录
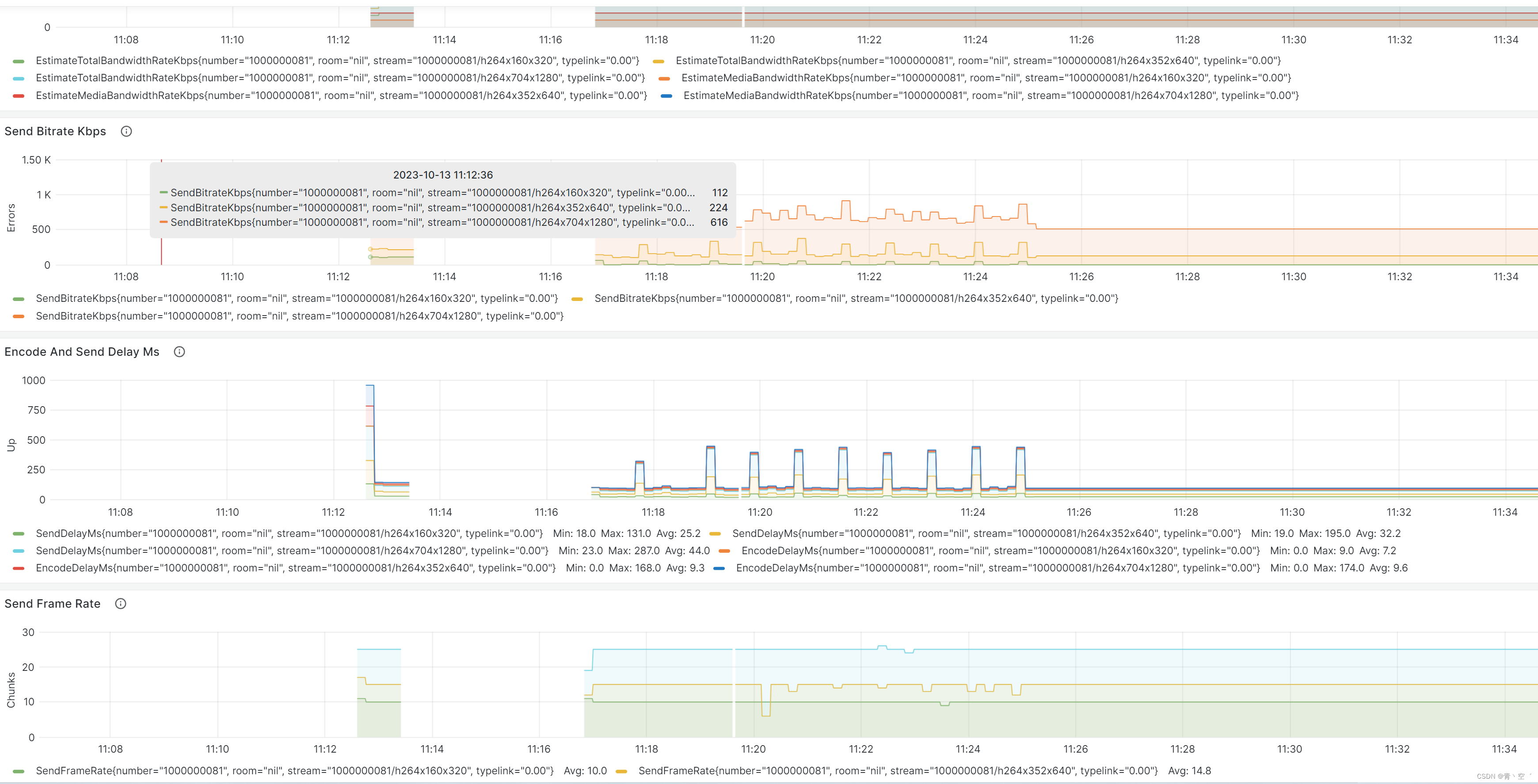
文章目录 json model导入申请api key创建dashboard删除dashboard json model导入 直接在ui通过json model 导入,开发自己用还好,但对非开发人员不太友好,故考虑通过api后台自动创建 api doc : https://grafana.com/docs/grafana/v9.3/devel…...

局域网上IP多播与IP单播关于MAC地址的区别
IP单播进行到局域网上的时候: 网际层使用IP地址进行寻址,各路由器收到IP数据报后,根据其首部中的目的IP地址的网络号部分,基于路由表进行查表转发。 查表转发的结果可指明IP数据报的下一跳路由器的IP地址,但无法指明…...

三数之和[中等]
优质博文:IT-BLOG-CN 一、题目 给你一个整数数组nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i ! j、i ! k且j ! k,同时还满足nums[i] nums[j] nums[k] 0。请你返回所有和为0且不重复的三元组。 注意:答案中不可以…...

基于天牛须优化的BP神经网络(分类应用) - 附代码
基于天牛须优化的BP神经网络(分类应用) - 附代码 文章目录 基于天牛须优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.天牛须优化BP神经网络3.1 BP神经网络参数设置3.2 天牛须算法应用 4.测试结果&#x…...

渗透波菜网站
免责声明 本文发布的工具和脚本,仅用作测试和学习研究,禁止用于商业用途,不能保证其合法性,准确性,完整性和有效性,请根据情况自行判断。如果任何单位或个人认为该项目的脚本可能涉嫌侵犯其权利,…...

Spring Boot:Dao层-实例介绍
目录 Dao层的作用Dao层的特点与 Service 层和 Controller 层的关系实例介绍MenuDaoOperatorLogDaoRoleDaoUserDao四个文件的共同点引用的包使用Repository注解继承JpaRepository接口接口的实体类的主键类型使用 Query()注解 Dao层的作用 负责与数据库进行交互,主要…...

接口测试入门:深入理解接口测试!
很多人会谈论接口测试。到底什么是接口测试?如何进行接口测试?这篇文章会帮到你。 一、前端和后端 在谈论接口测试之前,让我们先明确前端和后端这两个概念。 前端是我们在网页或移动应用程序中看到的页面,它由 HTML 和 CSS 编写…...
Redis微服务架构
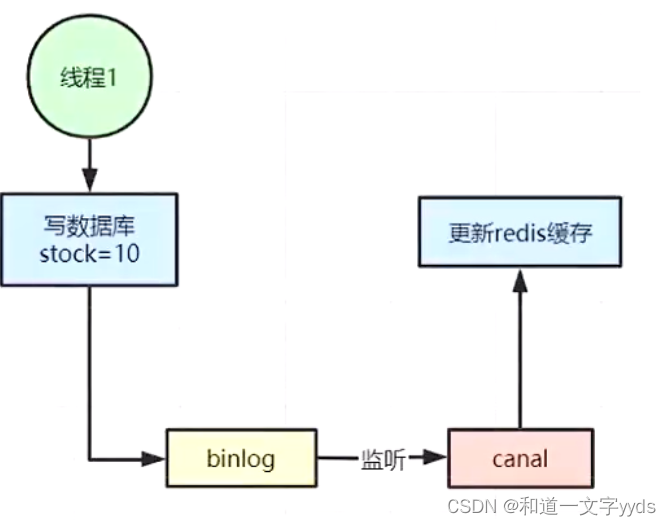
Redis微服务架构 缓存设计 缓存穿透 缓存穿透是指查询一个根本不存在的数据,缓存层和存储层都不会命中,通常出于容错的考虑,如果从存储层查不到数据则不写入缓层。 缓存穿透将导致不存在的数据每次请求都要到存储层去查询,失去…...

【C++】 局部对象,引用返回
1、new 关键字 会在堆内申请空间,如果仅仅是普通调用构造函数,不会在堆内开辟空间。 2、函数调用会形成栈帧,进行压栈操作,函数调用结束,会进行弹栈。 函数内的局部对象,会随着弹栈,而被销毁(…...

线性代数中涉及到的matlab命令-第二章:矩阵及其运算
目录 1,矩阵定义 2,矩阵的运算 3,方阵的行列式和伴随矩阵 4,矩阵的逆 5,克莱默法则 6,矩阵分块 1,矩阵定义 矩阵与行列式的区别: (1)形式上行列式…...

计算机毕业设计选什么题目好?springboot 美食推荐系统
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...
爆肝整理,Jmeter接口性能测试-跨线程调用变量实操(超详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、Jmeter中线程运…...
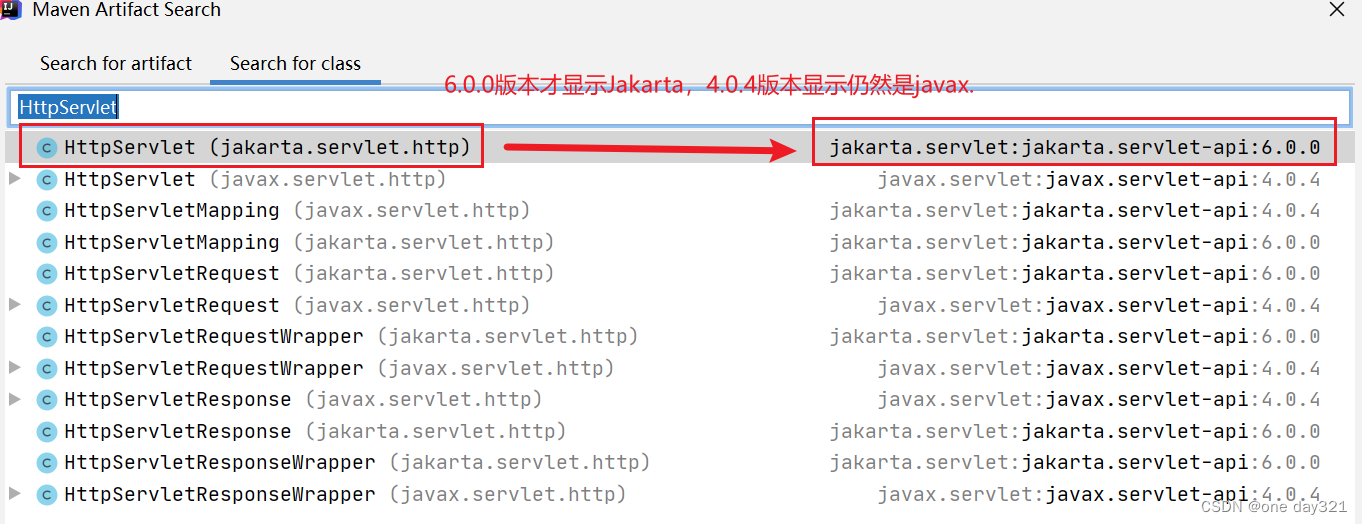
Maven导入程序包jakarta.servlet,但显示不存在
使用前提:(Tomcat10版本)已知tomcat10版本之后,使用jakart.servlet。而tomcat9以及之前使用javax.servlet。 问题描述:在maven仓库有导入了Jakarta程序包,但是界面仍然显示是javax。(下图&…...
es6(二)——常用es6说明
ES6的系列文章目录 es6(一)——var和let和const的区别 文章目录 ES6的系列文章目录一、变量的结构赋值1.数组的结构赋值2.对象的结构赋值 二、模板字符串三、扩展运算符1.字符串的使用2.数组的使用 四、箭头函数1.普通函数的定义2.箭头函数的定义3.箭头…...
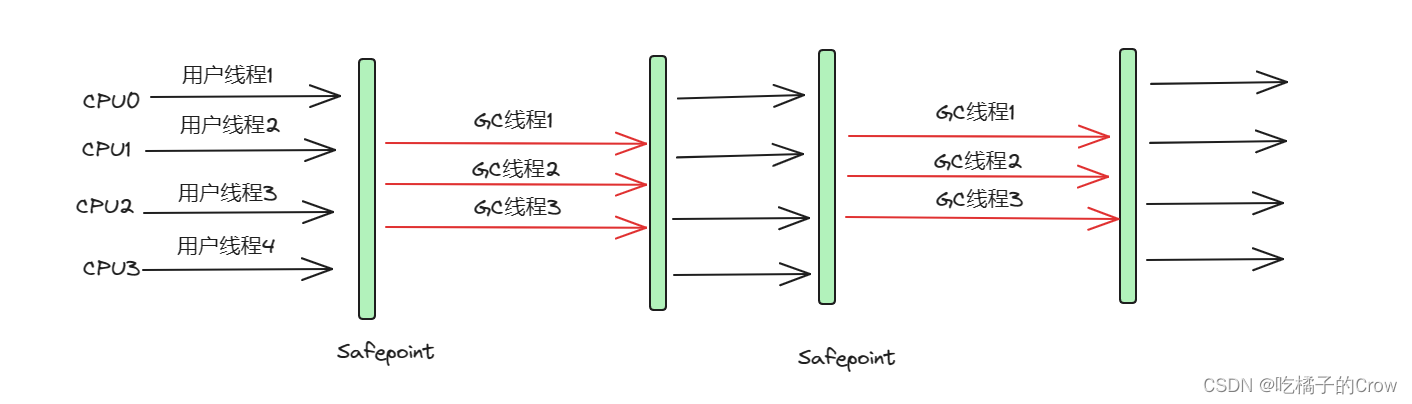
经典垃圾回收器
1.各垃圾回收器之间的配合使用关系 2.垃圾回收器的种类 2.1 Serial收集器(默认新生代收集器) Serial收集器是历史最悠久的收集器,曾经是新生代收集器的唯一选择,它是一个单线程工作的收集器,其“单线程”的意义不仅仅…...

台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法
台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法 台达触摸屏(B07S410)在上载程序时(显示No response from HMI)我以前的电脑是WIN7的,从来没出现过这样的问题,现在换成win10的,怎么都不行,(USB显示是一个大容量存储)换一台电脑(win10)有些行,有些不行…...

[资源推荐] 复旦大学张奇老师科研分享
刷B站的时候首页给我推了这个:【直播回放】复旦大学张奇教授亲授:人工智能领域顶会论文的发表指南先前也散漫地读了些许论文,但没有在一些宏观的方法论下去训练,读的时候能感觉出一些科研的套路,论文写作的套路&#x…...

C++数位动态规划算法:统计整数数目
题目 给你两个数字字符串 num1 和 num2 ,以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件,我们称它是一个好整数: num1 < x < num2 min_sum < digit_sum(x) < max_sum. 请你返回好整数的数目。答案可能很大&…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
