考研：数学二例题--∞−∞和0⋅∞型极限
| 前言 |
|---|
本文只是例题，建议先参考具体如何做这类型例题。请到主文章中参考：https://blog.csdn.net/grd_java/article/details/132246630
∞ − ∞ 和 0 ⋅ ∞ \infin - \infin 和 0·\infin ∞−∞和0⋅∞
| 例题 |
|---|
例1： lim x → + ∞ x 2 + x 2 − x 2 − x \begin{aligned} \lim\limits_{x \rightarrow +\infin} \sqrt[2]{x^2 + x} - \sqrt{x^2 - x} \\ \end{aligned} x→+∞lim2x2+x−x2−x
方法1：造分母
解：原式 = 分母看成 1 ，上下同乘 x 2 + x + x 2 − x lim x → + ∞ ( x 2 + x − x 2 − x ) ⋅ ( x 2 + x + x 2 − x ) x 2 + x + x 2 − x 解：原式 {\xlongequal{分母看成1，上下同乘 \sqrt{x^2 + x} + \sqrt{x^2 - x}} \lim\limits_{x \rightarrow +\infin} \frac{(\sqrt{x^2 + x} - \sqrt{x^2 - x}) · (\sqrt{x^2 + x} + \sqrt{x^2 - x})}{\sqrt{x^2 + x}+ \sqrt{x^2 - x}} } 解：原式分母看成1，上下同乘x2+x+x2−xx→+∞limx2+x+x2−x(x2+x−x2−x)⋅(x2+x+x2−x)
= lim x → + ∞ 2 x x 2 + x + x 2 − x = 发现变成 ∞ ∞ 型 , 同类型抓大头 ( x 2 + x 变成 x 2 = ∣ x ∣ , 注意开偶次方根后为绝对值，然后因为 x → ∞ , 所以 ∣ x ∣ = + x = x ) { = \lim\limits_{x \rightarrow +\infin} \dfrac{2x}{\sqrt{x^2 + x} + \sqrt{x^2 - x}} \xlongequal{发现变成\dfrac{\infin}{\infin}型,同类型抓大头(\sqrt{x^2 + x} 变成\sqrt{x^2} = \color{red}|x|,注意开偶次方根后为绝对值，然后因为x\rightarrow\infin,所以|x| = +x = x)} } =x→+∞limx2+x+x2−x2x发现变成∞∞型,同类型抓大头(x2+x变成x2=∣x∣,注意开偶次方根后为绝对值，然后因为x→∞,所以∣x∣=+x=x)
= lim x → + ∞ 2 x x + x = 1 \begin{aligned} =\lim\limits_{x \rightarrow +\infin} \dfrac{2x}{x+x} = 1 \\ \\ \end{aligned} =x→+∞limx+x2x=1方法2：倒代换，提项
解：原式 = 从 x 2 + x 中提出 ∣ x ∣ = > x 2 ( 1 + 1 x ) = ∣ x ∣ 1 + 1 x lim x → + ∞ x ( 1 + 1 x − 1 − 1 x ) ∣ x ∣ 到底取正还是负，要看条件，这里 x → + ∞ , 所以是正的 { 解：原式 \xlongequal{从\sqrt{x^2+x}中提出|x| => \sqrt{x^2(1+\frac{1}{x})} = |x|\sqrt{1+\frac{1}{x}}} \lim\limits_{x \rightarrow +\infin} x(\sqrt{1+\frac{1}{x}} - \sqrt{1-\frac{1}{x}}) \color{red} |x|到底取正还是负，要看条件，这里x\rightarrow +\infin,所以是正的 } 解：原式从x2+x中提出∣x∣=>x2(1+x1)=∣x∣1+x1x→+∞limx(1+x1−1−x1)∣x∣到底取正还是负，要看条件，这里x→+∞,所以是正的
= 可见变为了 0 ⋅ ∞ 型，用倒代换法令 t = 1 x lim t → 0 + 1 t ( 1 + t − 1 − t ) = lim t → 0 + ( 1 + t − 1 − t ) t { \xlongequal{可见变为了0·\infin型，用倒代换法令t = \dfrac{1}{x}} \lim\limits_{t \rightarrow 0^+} \dfrac{1}{t}(\sqrt{1+t}-\sqrt{1-t}) = \lim\limits_{t \rightarrow 0^+} \dfrac{(\sqrt{1+t}-\sqrt{1-t})}{t} } 可见变为了0⋅∞型，用倒代换法令t=x1t→0+limt1(1+t−1−t)=t→0+limt(1+t−1−t)
= 此时发现变为 0 0 型，可用洛必达和等价无穷小，这里用洛必达 = lim t → 0 + [ 1 2 ⋅ ( 1 + t ) − 1 2 + 1 2 ⋅ ( 1 + t ) − 1 2 ] = 1 注意是复合函数， 1 + t 和 1 − t 也得求导 {\begin{aligned} \xlongequal{此时发现变为\dfrac{0}{0}型，可用洛必达和等价无穷小，这里用洛必达} = \lim\limits_{t \rightarrow 0^+} [\dfrac{1}{2}·(1+t)^{-\dfrac{1}{2}} + \dfrac{1}{2}·(1+t)^{-\dfrac{1}{2}}] = 1 \color{red} 注意是复合函数，1+t和1-t也得求导 \\\\ \end{aligned}} 此时发现变为00型，可用洛必达和等价无穷小，这里用洛必达=t→0+lim[21⋅(1+t)−21+21⋅(1+t)−21]=1注意是复合函数，1+t和1−t也得求导等价无穷：(注意+ -操作时，两个项同级，代换后+ - 不为0才可以代换)
{ 1 、 ( 1 + □ ) α − 1 ∼ α □ 2 、 1 + □ − 1 = ( 1 + □ ) 1 2 − 1 ∼ 1 2 □ 例 1 、 1 + x − 1 ∼ 1 2 x 例 2 、 1 − x − 1 ∼ 1 2 ( − x ) 例 3 、 1 − 1 + x ∼ − 1 2 x 例 4 、 1 − 1 − x ∼ − 1 2 ( − x ) { \begin{cases} 1、 (1+□) ^ α -1 \thicksim α□ \\ 2、\sqrt{1+□} -1 = (1+□)^\frac{1}{2} -1 \thicksim \frac{1}{2} □\\ 例1、\sqrt{1+x} - 1 \thicksim \frac{1}{2} x \\ 例2、\sqrt{1-x} - 1 \thicksim \frac{1}{2} (-x) \\ 例3、1- \sqrt{1+x} \thicksim -\frac{1}{2} x \\ 例4、1-\sqrt{1-x} \thicksim - \frac{1}{2} (-x) \end{cases} } ⎩ ⎨ ⎧1、(1+□)α−1∼α□2、1+□−1=(1+□)21−1∼21□例1、1+x−1∼21x例2、1−x−1∼21(−x)例3、1−1+x∼−21x例4、1−1−x∼−21(−x)
则 lim t → 0 + ( 1 + t − 1 − t ) t = lim t → 0 + ( 1 + t − 1 ) − ( 1 − t − 1 ) t {\begin{aligned} 则 \lim\limits_{t \rightarrow 0^+} \dfrac{(\sqrt{1+t}-\sqrt{1-t})}{t} = \lim\limits_{t \rightarrow 0^+} \dfrac{(\sqrt{1+t}-1)-(\sqrt{1-t}-1)}{t}\\\\ \end{aligned}} 则t→0+limt(1+t−1−t)=t→0+limt(1+t−1)−(1−t−1)
= 等价代换得 lim t → 0 + ( 1 2 t ) − ( − 1 2 t ) t = 可见代换后 ( 1 2 t ) − ( − 1 2 t ) = 1 t 不为 0 可以代换 1 {\begin{aligned} \xlongequal{等价代换得} \lim\limits_{t \rightarrow 0^+} \dfrac{(\dfrac{1}{2}t)-(-\dfrac{1}{2}t)}{t} \xlongequal{可见代换后(\dfrac{1}{2}t)-(-\dfrac{1}{2}t) = 1t不为0可以代换} 1 \\\\ \end{aligned}} 等价代换得t→0+limt(21t)−(−21t)可见代换后(21t)−(−21t)=1t不为0可以代换1方法3：泰勒公式 ( 1 + □ ) a = 1 + a □ + a ( a − 1 ) 2 ! □ 2 + a ( a − 1 ) ( a − 2 ) 3 ! □ 3 + . . . + O ( x n ) (1+□)^a = 1+a□+\dfrac{a(a-1)}{2!}□^2+\dfrac{a(a-1)(a-2)}{3!}□^3+...+O(x^n) (1+□)a=1+a□+2!a(a−1)□2+3!a(a−1)(a−2)□3+...+O(xn)
= 参考前面的方法化简到 lim t → 0 + ( 1 + t − 1 − t ) t = 分母 t 为 1 次方，泰勒公式也展开到 1 次 {\begin{aligned} \xlongequal{参考前面的方法化简到}\lim\limits_{t \rightarrow 0^+} \dfrac{(\sqrt{1+t}-\sqrt{1-t})}{t} \xlongequal{分母t为1次方，泰勒公式也展开到1次} \\ \end{aligned}} 参考前面的方法化简到t→0+limt(1+t−1−t)分母t为1次方，泰勒公式也展开到1次
= lim t → 0 + [ 1 + 1 2 t + O ( t ) ] − [ 1 − 1 2 t + O ( t ) ] t = lim t → 0 + t + O ( t ) t = 1 {\begin{aligned} =\lim\limits_{t \rightarrow 0^+} \dfrac{[1+\dfrac{1}{2}t + O(t)] - [1-\dfrac{1}{2}t + O(t)]}{t} = \lim\limits_{t \rightarrow 0^+} \dfrac{t+O(t)}{t} = 1 \end{aligned}} =t→0+limt[1+21t+O(t)]−[1−21t+O(t)]=t→0+limtt+O(t)=1
注意：泰勒公式就是将复杂极限换成多项式（容易求导） + 余项（无限趋近于 0 的与原极限的误差） , 而这个多项式无限趋近于原来的极限 . 所以几倍的 O ( t ) 无需担心， 2 O ( t ) 可以直接总结为 O ( t ) ，最终给出计算结果时，可以省略余项，但是过程中需要带上这个余项 {\begin{aligned} \color{red} 注意：泰勒公式就是将复杂极限换成多项式（容易求导）+余项（无限趋近于0的与原极限的误差）,而这个多项式无限趋近于原来的极限.\\ \color{red} 所以几倍的O(t)无需担心，2O(t)可以直接总结为O(t)，最终给出计算结果时，可以省略余项，但是过程中需要带上这个余项 \\\\\end{aligned} } 注意：泰勒公式就是将复杂极限换成多项式（容易求导）+余项（无限趋近于0的与原极限的误差）,而这个多项式无限趋近于原来的极限.所以几倍的O(t)无需担心，2O(t)可以直接总结为O(t)，最终给出计算结果时，可以省略余项，但是过程中需要带上这个余项方法4：拉格朗日中值定理 f ( b ) − f ( a ) = f ′ ( ξ ) ⋅ ( b − a ) f(b) - f(a) = f^{'}(\xi)·(b-a) f(b)−f(a)=f′(ξ)⋅(b−a)
= 参考前面方法化简到 lim t → 0 + ( 1 + t − 1 − t ) t = f ( t ) = 1 + t , f ( − t ) = 1 − t , f ′ ( ξ ) = 1 2 1 + ξ ⋅ 1 ，（ 1 是因为复合函数，需要乘 1 + t 的导数） {\begin{aligned} \xlongequal{参考前面方法化简到}\lim\limits_{t \rightarrow 0^+} \dfrac{(\sqrt{1+t}-\sqrt{1-t})}{t} \xlongequal{f(t) = \sqrt{1+t},f(-t) = \sqrt{1-t}, f^{'}(\xi) = \dfrac{1}{2\sqrt{1+\xi}}·1，（1是因为复合函数，需要乘1+t的导数）} \\ \end{aligned}} 参考前面方法化简到t→0+limt(1+t−1−t)f(t)=1+t,f(−t)=1−t,f′(ξ)=21+ξ1⋅1，（1是因为复合函数，需要乘1+t的导数）
= lim t → 0 + f ( t ) − f ( − t ) t = 根据拉格朗日定理得 lim t → 0 + 1 2 1 + ξ ⋅ 2 t t {\begin{aligned} =\lim\limits_{t \rightarrow 0^+} \dfrac{f(t)-f(-t)}{t} \xlongequal{根据拉格朗日定理得} \lim\limits_{t \rightarrow 0^+} \dfrac{\dfrac{1}{2\sqrt{1+\xi}}·2t}{t} \end{aligned}} =t→0+limtf(t)−f(−t)根据拉格朗日定理得t→0+limt21+ξ1⋅2t
lim t → 0 + 1 2 ⋅ 2 t t = 1 。这一步是根据拉格朗日定理，有 − t < ξ < t , 又因为夹逼准则（两边趋于 0 ，中间那个也趋于 0 ） t 和 − t 都趋向于 0 ，则 ξ 也趋于 0 ，所以 1 + ξ ∼ 1 {\begin{aligned} \lim\limits_{t \rightarrow 0^+} \dfrac{\dfrac{1}{2}·2t}{t} = 1。这一步是 根据拉格朗日定理，有-t<\xi<t,又因为夹逼准则（两边趋于0，中间那个也趋于0）t和-t都趋向于0，则\xi也趋于0，所以\sqrt{1+\xi} \thicksim 1 \\\\\end{aligned} } t→0+limt21⋅2t=1。这一步是根据拉格朗日定理，有−t<ξ<t,又因为夹逼准则（两边趋于0，中间那个也趋于0）t和−t都趋向于0，则ξ也趋于0，所以1+ξ∼1
例2: lim x → + ∞ x 2 ( 2 1 x − 2 1 x + 1 ) \begin{aligned} \lim\limits_{x \rightarrow +\infin} x^2 (2^{\frac{1}{x}} - 2^{\frac{1}{x+1}}) \end{aligned} x→+∞limx2(2x1−2x+11)
方法1：提项 e □ − e △ = e △ ( e □ − △ − 1 ) e^□ - e^△ = e^△(e^{□ -△}-1) e□−e△=e△(e□−△−1),e为任意值，等价无穷小 a x − 1 = x l n a a^x - 1 = xlna ax−1=xlna
{ 原式 = lim x → + ∞ x 2 ⋅ 2 1 x + 1 ( 2 1 x − 1 x + 1 − 1 ) = x → + ∞ , 2 1 x + 1 → 1 lim x → + ∞ x 2 ⋅ 1 ( 2 1 x ( x + 1 ) − 1 ) = 等价无穷小， x → + ∞ 时 ( 2 1 x ( x + 1 ) − 1 ) → 0 lim x → + ∞ x 2 ⋅ 1 x ( x + 1 ) l n 2 = 抓大头，将 1 舍去 lim x → + ∞ x 2 x 2 l n 2 = l n 2 \begin{cases} 原式=\lim\limits_{x\rightarrow+\infin} x^2 \cdot 2^{\frac{1}{x+1}}(2^{\frac{1}{x}-\frac{1}{x+1}}-1) \xlongequal{x \rightarrow +\infin, 2^{\frac{1}{x+1}}\rightarrow 1} \lim\limits_{x\rightarrow+\infin} x^2 \cdot 1 (2^{\frac{1}{x(x+1)}}-1) \\ \xlongequal{等价无穷小，x\rightarrow+\infin时(2^{\frac{1}{x(x+1)}}-1) \rightarrow0} \lim\limits_{x\rightarrow+\infin} x^2 \cdot {\frac{1}{x(x+1)}}ln2 \xlongequal{抓大头，将1舍去} \lim\limits_{x\rightarrow+\infin} \frac{x^2}{x^2}ln2 = ln2 \\\\\end{cases} ⎩ ⎨ ⎧原式=x→+∞limx2⋅2x+11(2x1−x+11−1)x→+∞,2x+11→1x→+∞limx2⋅1(2x(x+1)1−1)等价无穷小，x→+∞时(2x(x+1)1−1)→0x→+∞limx2⋅x(x+1)1ln2抓大头，将1舍去x→+∞limx2x2ln2=ln2
方法2：拉格朗日中值定理： f ( a ) − f ( b ) = f ′ ( ξ ) ( b − a ) , a < ξ < b f(a)-f(b) = f\rq(\xi)(b-a),a<\xi<b f(a)−f(b)=f′(ξ)(b−a),a<ξ<b
{ 1 、令 f ( t ) = 2 t ， f ′ ( t ) = 2 t l n 2 , 则根据拉格朗日中值定理有 f ( 1 x ) − f ( 1 x + 1 ) = 2 1 x + 1 − 2 1 x = 2 ξ l n 2 ( 1 x + 1 − 1 x ) 2 、则 1 x + 1 < ξ < 1 x , 当 x → + ∞ 时， 1 x + 1 和 1 x 趋向于 0 ，由夹逼定理可得 ξ → 0 ，则 2 ξ → 1 原式 = lim x → + ∞ x 2 ( 2 ξ l n 2 ( 1 x + 1 − 1 x ) ) = lim x → + ∞ x 2 ( 1 x + 1 − 1 x ) l n 2 = 抓大头，将 1 舍去 lim x → + ∞ x 2 x 2 l n 2 = l n 2 \begin{cases}\\ 1、令f(t) = 2^t，f\rq(t) = 2^tln2 ,则根据拉格朗日中值定理有 f(\frac{1}{x})-f(\frac{1}{x+1}) =2^\frac{1}{x+1}-2^\frac{1}{x}= 2^\xi ln2(\frac{1}{x+1}-\frac{1}{x})\\\\ 2、则\frac{1}{x+1}<\xi <\frac{1}{x}, 当x\rightarrow+\infin时，\frac{1}{x+1}和\frac{1}{x}趋向于0，由夹逼定理可得 \xi \rightarrow 0，则2^\xi \rightarrow 1\\ 原式=\lim\limits_{x\rightarrow+\infin} x^2(2^\xi ln2(\frac{1}{x+1}-\frac{1}{x})) = \lim\limits_{x\rightarrow+\infin} x^2(\frac{1}{x+1}-\frac{1}{x})ln2 \xlongequal{抓大头，将1舍去} \lim\limits_{x\rightarrow+\infin} \frac{x^2}{x^2}ln2 = ln2 \\\\\end{cases} ⎩ ⎨ ⎧1、令f(t)=2t，f′(t)=2tln2,则根据拉格朗日中值定理有f(x1)−f(x+11)=2x+11−2x1=2ξln2(x+11−x1)2、则x+11<ξ<x1,当x→+∞时，x+11和x1趋向于0，由夹逼定理可得ξ→0，则2ξ→1原式=x→+∞limx2(2ξln2(x+11−x1))=x→+∞limx2(x+11−x1)ln2抓大头，将1舍去x→+∞limx2x2ln2=ln2
相关文章：
考研：数学二例题--∞−∞和0⋅∞型极限
前言 本文只是例题，建议先参考具体如何做这类型例题。请到主文章中参考：https://blog.csdn.net/grd_java/article/details/132246630 ∞ − ∞ 和 0 ⋅ ∞ \infin - \infin 和 0\infin ∞−∞和0⋅∞ 例题 例1： lim x → ∞ x 2 x 2 −…...
C++算法：图中的最短环
题目 现有一个含 n 个顶点的 双向 图，每个顶点按从 0 到 n - 1 标记。图中的边由二维整数数组 edges 表示，其中 edges[i] [ui, vi] 表示顶点 ui 和 vi 之间存在一条边。每对顶点最多通过一条边连接，并且不存在与自身相连的顶点。 返回图中 …...
C++学习——类其实也是一种作用域
以下内容源于C语言中文网的学习与整理，非原创，如有侵权请告知删除。 其实也是一种作用域，每个类都会定义它自己的作用域。在类的作用域之外，普通的成员只能通过对象（可以是对象本身，也可以是对象指针或对象…...
Seata入门系列【4】undo_log、global_table、branch_table、lock_table字段及作用详解
1 客户端 1.1 undo_log 在AT模式中，需要在参与全局事务的数据库中，添加一个undo_log表，建表语句如下： SET NAMES utf8mb4; SET FOREIGN_KEY_CHECKS 0;-- ---------------------------- -- Table structure for undo_log -- --…...
虚幻引擎：数据表格的C++常用API
1.将数据表格中的所有数据存到一个数组中 //参数1 // 错误提示 //参数2 // 存储的数组 TArray<FKeyInfoHeader*> array; KeyInfoDT->GetAllRows<FKeyInfoHeader>(TEXT("错误"),array); 2.获取表格中所有的行名称 TArray<FName>array; …...
Java日期格式化（DateFormat类和SimpleDateFormat类）
格式化日期表示将日期/时间格式转换为预先定义的日期/时间格式。例如将日期“Fri May 18 15:46:24 CST2016” 格式转换为 “2016-5-18 15:46:24 星期五”的格式。 在 java 中，可以使用 DateFormat 类和 SimpleDateFormat 类来格式化日期，下面详细介绍这两…...
centos 7 lamp owncloud
OwnCloud是一款开源的云存储软件，基于PHP的自建网盘。基本上是私人使用，没有用户注册功能，但是有用户添加功能，你可以无限制地添加用户，OwnCloud支持多个平台（windows，MAC，Android&a…...
屏幕亮度调节保护您的眼睛
官方下载地址： 安果移动 视频演示：屏幕亮度调节-保护您的眼睛_哔哩哔哩_bilibili 嗨，亲爱的用户，你是否有过这样的体验：夜晚安静的时刻，想要在抖音上看看热门的舞蹈、在快手上发现生活的 趣味、或是在哔…...
CentOS Linux下CMake二进制文件安装并使用Visual Studio调试
cmake安装——二进制安装(很简单，推荐！！) 1）下载二进制包。首先就是官网下载二进制安装包(我们是64位系统，就下载对应的包)，这里。 例如：在/home/DOWNLOAD目录下执行，即下载二进制…...
ASP.net相关目录，相关配置文件和.后缀名解释
App_Data：用于存储应用程序的数据文件，例如数据库文件或其他本地文件。 App_Start：包含应用程序的启动配置文件，例如路由配置、日志配置等。 Content：存放应用程序的静态资源文件，如 CSS、JavaScript、图…...
一键批量转换，轻松将TS视频转为MP4视频，实现更广泛的播放和分享！
在享受精彩视频内容的同时，有时我们可能会面临一个问题：某些视频格式可能不太适合我们的播放设备或分享平台。特别是TS格式的视频，在一些情况下可能无法直接播放或上传。但是不用担心，因为我们为您提供了一款强大的视频剪辑工具&a…...
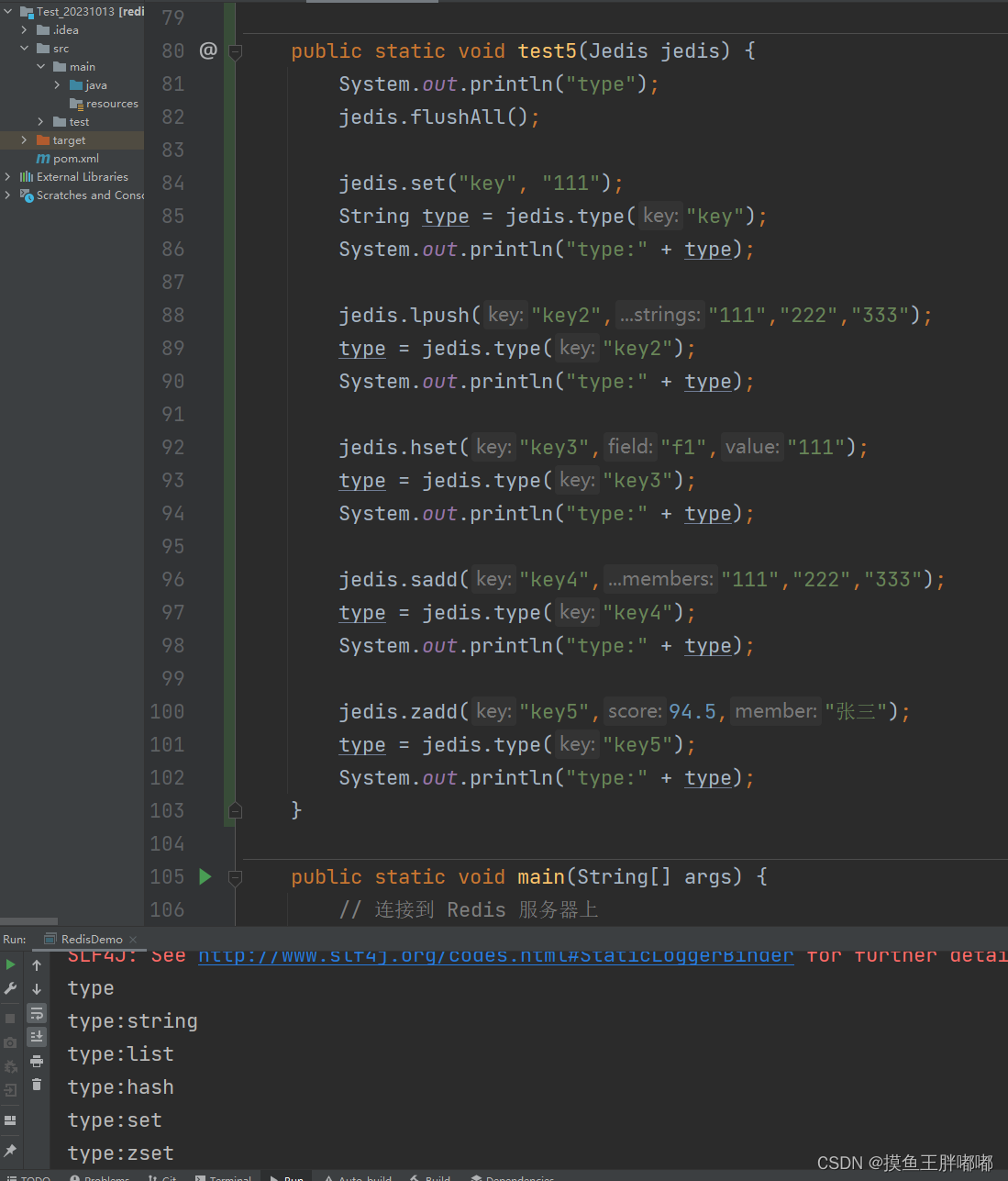
【Redis】使用Java客户端操作Redis
目录 引入jedis依赖连接Redis命令get/setexists/delkeysexpire/ttltype 引入jedis依赖 连接Redis 命令 get/set exists/del keys expire/ttl type...
BSPHP 未授权访问 信息泄露
漏洞描述 BSPHP 存在未授权访问 泄露用户 IP 和 账户名信息 漏洞复现 访问url： 构造payload访问： /admin/index.php?madmin&clog&atable_json&jsonget&soso_ok1&tuser_login_log&page1&limit10&bsphptime16004073…...
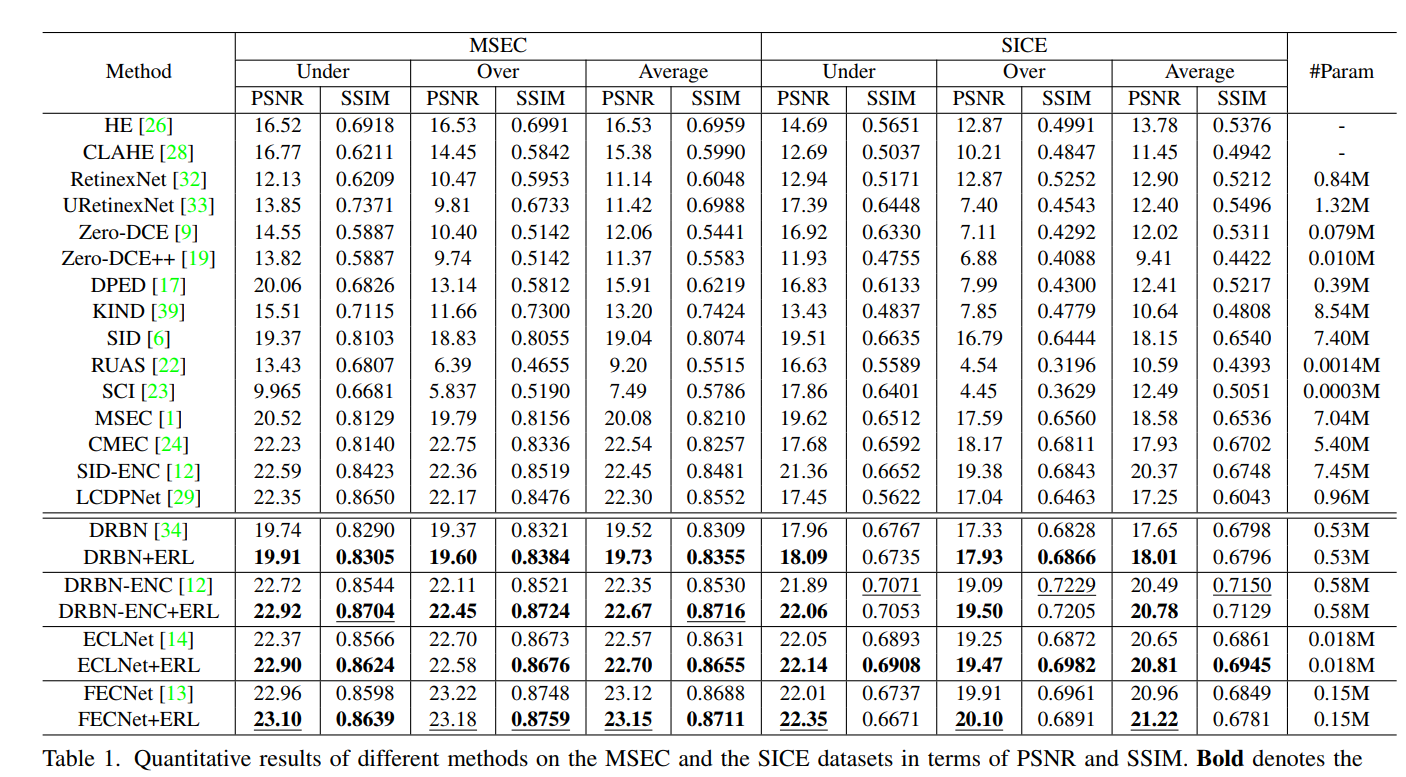
Learning Sample Relationship for Exposure Correction 论文阅读笔记
这是中科大发表在CVPR2023的一篇论文，提出了一个module和一个损失项，能够提高现有exposure correction网络的性能。这已经是最近第三次看到这种论文了，前两篇分别是CVPR2022的ENC（和这篇文章是同一个一作作者）和CVPR20…...
Vue项目 -- 解决Eslint导致的console报错问题
在利用vue-cli3构建的项目中引入eslint进行语法检查时，使用console.log(‘xxx’)时，控制台抛出了Unexpected console statement (no-console) 异常， 例：一使用console就提示报错 解决办法是： 在 .eslintrc.js 文件中…...
uni-app 在已有的数据对象中动态添加更多的数据对象
原数据对象 flowData: {list: [], // 数据值column: 2, // 瀑布列数columnSpace: 2 // 瀑布列宽间距 } 动态添加后的数据对象 flowData: {list: [], // 数据值column: 2, // 瀑布列数columnSpace: 2, // 瀑布列宽间距column_1: [],column_2: [] } 动态添加更多的数据对象的…...
【LeetCode】17. 电话号码的字母组合
1 问题 给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。 示例 1： 输入：digits “23” 输出&…...
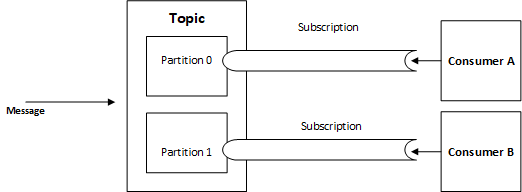
使用 Apache Kafka 进行发布-订阅通信中的微服务
发布-订阅消息系统在任何企业架构中都发挥着重要作用，因为它可以实现可靠的集成，而无需紧密耦合应用程序。在解耦的系统之间共享数据的能力并不是一个容易解决的问题。 考虑一家拥有多个使用不同语言和平台独立构建的应用程序的企业。它需要响应地共享数…...
valarray 包含对象成员的类（cpp14章）
C代码重用 1.公有继承可以实现 2.包含、私有继承、保护继承用于实现has-a关系，即新的类将包含另一个类的对象。 （使用这样类成员：本身是另外一个类对象称为包含 （组合或层次化）。） 3.函数模板、类模…...
2023双11笔记本电脑候选名单(截止2023.10.13的价格,双十一活动可能会更便宜一点)
以下是我最近几天查阅抖音,B站,知乎,百度,朋友后候选出来的一些6000-8000的游戏本电脑,标绿的属性是相比之下较为优秀的 附上几个网上的CPU和显卡排行网站 CPU性能排行榜 - CPU天梯图 - 最强CPU2023(较为全面的CPU排行,收录四千多款) 笔记本性能排行榜 - 快科技天梯榜 笔记本CP…...
Springcloud笔记（4）-客户端负载均衡Ribbon
Ribbon是一个基于HTTP和TCP的客户端负载均衡工具，不需要独立部署，几乎存在于每一个springcloud构建的微服务和基础设施中。 微服务间调用，API网关的请求转发都通过Ribbon实现。 负载均衡 通常所说的负载均衡都是指的服务端负载均衡…...
MediaRecorder媒体录音机
权限： <uses-permission android:name"android.permission.RECORD_AUDIO"/> <uses-permission android:name"android.permission.WRITE_EXTERNAL_STORAGE"/> <uses-permission android:name"android.permission.READ_EXTE…...
短视频如何批量添加水印
在当今的数字时代，短视频已经成为一种非常流行的内容形式。无论是社交媒体还是视频分享网站，短视频都已经成为了一种非常有吸引力的内容。然而，对于一些拥有大量视频内容的创作者来说，添加水印可能是一项繁琐的任务。本文将介绍如…...
RT-Thread MQTT（学习）
MQTT背景应用 MQTT是机器对机器（M2M）/物联网（IoT）连接协议，英文全名为“Message Queuing Telemetry Transport”，“消息队列遥测传输”协议。它是专为受限设备和低带宽、高延迟或不可靠的网络而设计的&…...
Vue_Bug VUE-ELEMENT-ADMIN默认是英文模式
Bug描述： VUE-ADMIN-TEMPLATE-MASTER VUE-ELEMENT-ADMIN-MASTER 两个项目直接从GitHub上拉取下来 默认是英文模式 其他信息： 这两个项目默认支持中文语言包，无需额外引入，只需删除英文语言包依赖 //import enLang from element-…...
Spark中的Driver、Executor、Stage、TaskSet、DAGScheduler等介绍
工作流程： Driver 创建 SparkSession 并将应用程序转化为执行计划，将作业划分为多个 Stage，并创建相应的 TaskSet。Driver 将 TaskSet 发送给 TaskScheduler 进行调度和执行。TaskScheduler 根据资源情况将任务分发给可用的 Executor 进程执…...
docker的资源限制参数设置错误，导致的clickhouse性能瓶颈
使用场景 我们使用docker作为服务的虚拟化工具，服务都部署在docker里我们使用docker-compose管理所有docker服务的配置文件针对某些服务，我们要限制这个docker占用的资源数量，例如，cpu和内存在进行配置时，网上搜了一些…...
Vue路由守卫有哪些，怎么设置，有哪些使用场景？
Vue 路由守卫是在 Vue Router 中提供的一种功能，它允许您在导航到某个路由前、路由变化时或导航离开某个路由时执行代码。Vue 路由守卫提供了以下几种类型： 1.全局前置守卫 router.beforeEach 在进入路由前执行的钩子函数，它会接收三个参数&a…...
云原生网关可观测性综合实践
作者：钰诚 可观测性 可观测性（Observability）是指系统、应用程序或服务的运行状态、性能和行为能够被有效地监测、理解和调试的能力。 随着系统架构从单体架构到集群架构再到微服务架构的演进，业务越来越庞大，也越来…...
vue-element-admin—登录页面添加自定义背景
一、效果图 初始效果： 更改背景后效果： 二、操作步骤 1、准备图片 2、更改代码 打开下面路径的 index.vue 文件： vue-element-admin-master\src\views\login\index.vue 也就是登录页面。 对 .login-container 样式代码块内代码做如下…...