【Hello Algorithm】暴力递归到动态规划(四)
动态规划的数组压缩技巧 - 机器人走格子问题
题目是leetcode62题目原题 表示如下
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?

递归版本
我们首先来想递归函数的含义 它会返回给我们一个int类型的数据 这个数据就是我们的最大路径数
我们需要给这个函数 我们当前的位置 我们需要去到的位置 整体函数如下
int _uniquePaths(int x , int y ,int m , int n)
其中 x y 代表我们当前位置的坐标 m n代表要到达位置的坐标
接下来我们想base case
因为这是一个位置限制的棋盘 所以说我们要考虑是否会越界的问题 即
if (x > m || y > n){return 0;}
当然 当我们的走到finish位置的时候也算是结束了 会返回给我们一种路径方法 表示如下
if (x == m && y == n){return 1;}
接下来我们就开始列举各种可能性 因为我们这里只能往下或者是往右走 所以说一共有两种可能性
我们只需要把这两种可能性所需要的路径和相加就可以了 代码表示如下
int _uniquePaths(int x , int y ,int m , int n){// base caseif (x > m || y > n){return 0;}if (x == m && y == n){return 1;}int p1 = _uniquePaths(x + 1 , y, m, n);int p2 = _uniquePaths(x, y + 1, m, n);return p1 + p2;}
动态规划
接下来我们开始动态规划版本的代码改写
首先我们找出一直变化的变量是什么
int _uniquePaths(int x , int y ,int m , int n)
我们发现递归中一直变化的参数其实只有两个 x 和 y
所以说我们只需要建立一张x和y的二维表就可以
x的格子一共有m个 y的格子一共有n个 所以说 x的大小可以设置为 0 ~ m-1 y的大小可以设置为0 ~ n-1
我们要知道的是 x和y可能会越界 所以说我们要设置一个pickup函数来从表中选值 如果说越界了我们直接返回0即可
int pickup_dp(int x , int y , int m , int n , vector<vector<int>>& dp){if (x > m || y > n){return 0;}return dp[x][y];}
接下来我们来看base case
if (x == m && y == n){return 1;}
也就是说 当x为最大值 y为最大值的时候 此时dp表设置为1
dp[m-1][n-1] = 1;
接下来我们开始找位置依赖关系
int p1 = _uniquePaths(x + 1 , y, m, n);int p2 = _uniquePaths(x, y + 1, m, n);
假设这个格子是表中任意一个 图中表示为黑色的格子

那么依赖的格子就是红色的
根据依赖关系 我们可以从右往左 从下往上的方式 来填写依赖关系 代码表示如下
int dp_uniquePaths(int m , int n , vector<vector<int>>& dp){dp[m-1][n-1] = 1;for (int col = n -1 ; col >= 0 ; col--){for (int row = m -1; row >= 0; row--){if (row == m-1 && col == n-1){continue;}int p1 = pickup_dp(row + 1, col, m, n, dp);int p2 = pickup_dp(row , col + 1, m, n, dp);dp[row][col] = p1 + p2; }}return dp[0][0];}
这就是这道题目的动态规划解法
数组压缩技巧
我们可以发现的是 其实每个格子都只依赖于该列和它的右边一列 那么我们就可以使用两个列来表示整个二维表
也就是二维表转化为一维表 节省一定的空间
压缩技巧也很简单 只需要一列一列的转化就可以
代码表示如下
class Solution {
public:int pickup_dp(int x , int m , vector<int>& dp){if (x >= m || x < 0){return 0;}return dp[x];}int dp_uniquePaths(int m , int n ){// col1 prev // col2 curvector<int> col1(m , 0);vector<int> col2(m , 0);col1[m-1] = 1;for (int i = 0; i < n ; i++){for(int j = m - 1; j >= 0; j--){col2[j] = pickup_dp(j + 1, m, col2) + col1[j]; }for(int j = m -1 ; j >= 0 ; j--){col1[j] = col2[j];}}return col2[0];}int uniquePaths(int m, int n) {return dp_uniquePaths(m , n );}
};
我们这里稍微讲解下两列的转化思路
我们设定 col1为前一列 col2为当前列
每次我们修改col2内部的值 到最后我们全部修改完毕要到下一列的时候 我们更新下col1列的所有值
钱包问题一
我们给定一个数组 arr 数组里面的值表示任意一张面值的钞票
每张钞票代表的值可能相同 但是我们认为它们是不同的钞票
现在我们给定一个 val 值 请问有多少种组合方案可以让val值为0
递归解法
还是一样 我们首先来想函数
它要返回给我们一个组合的最大值 所以说我们的返回值要是一个int类型的数值
我们要遍历整个money数组 所以说我们需要这个数组和一个index参数来遍历
接着我们需要一个rest参数来记录剩余零钱的数目
整体函数如下
int process(vector<int>& money , int index , int rest)
接下来我们开始想base case
这道题目中有两个变化的量 我们首先向有没有可能会因为index而终止递归呢?
当然有 如果index越界了 那么我们的递归也就终止了
有没有可能因为rest而终止递归呢 ?
当然有 如果剩余零钱的数目为0 我们就终止递归了
if (rest < 0) { return 0; } int N = static_cast<int>(money.size()); if (index == N) { return rest == 0 ? 1 : 0; } 接下来开始列举可能性 对于这种从左往右的模型来说 可能性就是要和不要两种情况
所以说我们直接列出这两种可能性之后想加即可
int process(vector<int>& money , int index , int rest)
{ if (rest < 0) { return 0; } int N = static_cast<int>(money.size()); if (index == N) { return rest == 0 ? 1 : 0; } int p1 = process(money , index + 1 , rest); int p2 = process(money , index +1 , rest - money[index]); return p1 + p2;
}
动态规划
我们首先观察递归函数
int process(vector<int>& money , int index , int rest)
我们可以发现 其中变化的变量有 index 和 rest
所以说我们可以围绕着index 和 rest建立一张二维表
index 的大小是 0 ~ index 大小是index + 1
rest 的大小是 0 ~ rest 大小是rest + 1
我们建立完一个二维表之后就可以根据base case填写数据了
根据
if (index == N) { return rest == 0 ? 1 : 0; }
我们可以得出
dp[N][0] = 1;
接着我们来看位置依赖关系

它依赖于下面一行的两个格子
所以说我们从最下面的倒数第二行开始填写数据 为了防止越界问题 我们再写一个pickup函数
完整代码如下
int dpprocess(vector<int>& money , int rest)
{ int N = static_cast<int>(money.size()); vector<vector<int>> dp(N + 1 , vector<int>(rest + 1 , 0)); dp[N][0] = 1; for (int row = N - 1; row >= 0; row--){ for (int col = 0; col <= rest; col++) {dp[row][col] = pickupdp(row + 1 , col , dp , N , rest) + pickupdp(row + 1 , col - money[row] , dp , N , rest);}}return dp[0][rest];
}
钱包问题二
我们给定一个数组 arr 数组里面的值表示任意一张面值的钞票 arr内部值不同
每一个arr中的元素代表有无数张钞票
现在我们给定一个 val 值 请问有多少种组合方案可以让val值为0
这个问题和问题一的区别就是 在问题2中 我们的钱包有无数张钞票 只是它们的面值不同 要我们求解法
递归版本
我们首先来想 我们要写什么样的一个递归函数
我们要让这个函数返回一个最大的组合方案 所以返回值是一个int类型的数据
而我们要在一个数组中选取数据 所以自然而然的想到使用index遍历
最后我们还需要一个rest来表示剩余值 整体表示如下
int process(vector<int>& money , int index , int rest)
接着就是想base case 这一步照抄钱包问题一即可
到了列举可能性的这一步就有点意思了
此时的问题就从要不要变为了两个问题
- 要不要?
- 要的话要几个
所以说我们的代码也要转变下
int p1 = process(money , index + 1 , rest); // how many ? int p2 = 0; for (int fix = 1 ; fix * money[index] <= rest; fix++) { p2 += process(money , index + 1 , rest - fix * money[index]); }
可能性1就是我们不要这种类型的钞票了
可能性2就是我们要这种类型的钞票 一张张枚举 知道rest小于0为止
当然我们其实可以让fix从0开始 这样就不需要可能性1了
整体代码表示如下
int process(vector<int>& money , int index , int rest)
{if (rest < 0){return 0;}int N = static_cast<int>(money.size());if (index == N){return rest == 0 ? 1 : 0;}int p1 = process(money , index + 1 , rest); // how many ? int p2 = 0; for (int fix = 1 ; fix * money[index] <= rest; fix++) { p2 += process(money , index + 1 , rest - fix * money[index]); } return p1 + p2;
}
动态规划
我们首先观察递归函数
int process(vector<int>& money , int index , int rest)
我们可以发现 变量只有index 和rest
所以我们可以围绕着index和rest来做一张二维表
index 的大小是 0 ~ index 大小是index + 1
rest 的大小是 0 ~ rest 大小是rest + 1
我们建立完一个二维表之后就可以根据base case填写数据了
根据
if (index == N) { return rest == 0 ? 1 : 0; }
我们可以得出
dp[N][0] = 1;
接下来我们来看为止依赖关系

我们可以发现这个位置依赖于下面一行的数据具体的格子数目不确定
所以说我们就可以写出这样子的代码
for (int row = N - 1; row >= 0; row--) { for(int col = 0; col <= rest; col++) { int ways = 0; for (int fix = 0; fix * money[row] <= rest; fix++) { ways += pickupdp(row + 1 , col - fix * money[row] , dp , N , rest ); } dp[row][col] = ways; } }
动态规划优化
我们还是来观察下图
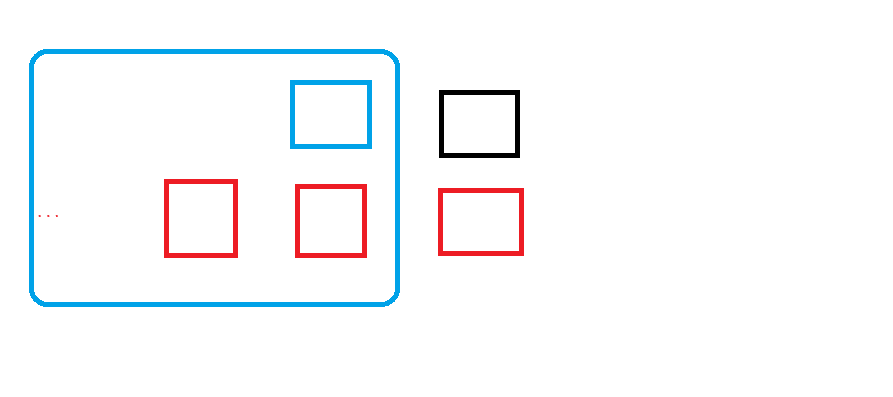
我们可以发现蓝色格子依赖的红色格子其实只比黑色格子依赖的红色格子少一个
也就是说我们可以这么转化
黑色格子依赖于蓝色格子和它下面的一个红色格子
于是我们的代码就可以这样子改写
int dpprocess(vector<int>& money , int rest)
{ int N = static_cast<int>(money.size()); vector<vector<int>> dp(N + 1 , vector<int>(rest + 1 , 0)); dp[N][0] = 1; for (int row = N - 1; row >= 0; row--) { for(int col = 0; col <= rest; col++) { dp[row][col] = pickupdp(row , col - money[row] , dp , N ,rest) + pickupdp(row + 1 , col , dp , N , rest); } } return dp[0][rest];
}
这样子我们就把原来的三个for循环优化成为了两个for循环 效率提高了不少
钱包问题三
我们给定一个数组 arr 数组里面的值表示任意一张面值的钞票 arr内部有相同值的钞票 我们认为值相同的钞票位置可以随意替换 (和题目一不同 题目一中每张钞票都是不同的 )
现在我们给定一个 val 值 请问有多少种组合方案可以让val值为0
这问题其实是题目二的变形
这里我提供一种思路将其转化为题目二 具体的代码大家可以自己尝试下
我们统计有多少种不同的钞票 并且将这些钞票添加到一个数组中
统计每个钞票的数目 再做一个数组
其中 第一个数组的用途和钱包问题二中的用途一样 而第二个数组则约束了每张钞票最多能取多少
之后按照钱包问题二的思路去做即可
相关文章:

【Hello Algorithm】暴力递归到动态规划(四)
动态规划的数组压缩技巧 - 机器人走格子问题 题目是leetcode62题目原题 表示如下 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中…...

arm day 8
arm 写一段按键中断代码 main.c #include "uart.h" #include "key_it.h" int main() {char c;char *s;uart4_init();//串口初始化//中断初始化key_it_config();while(1){//保证主程序不结束}return 0; } src/key_it.c #include"key_it.h"voi…...
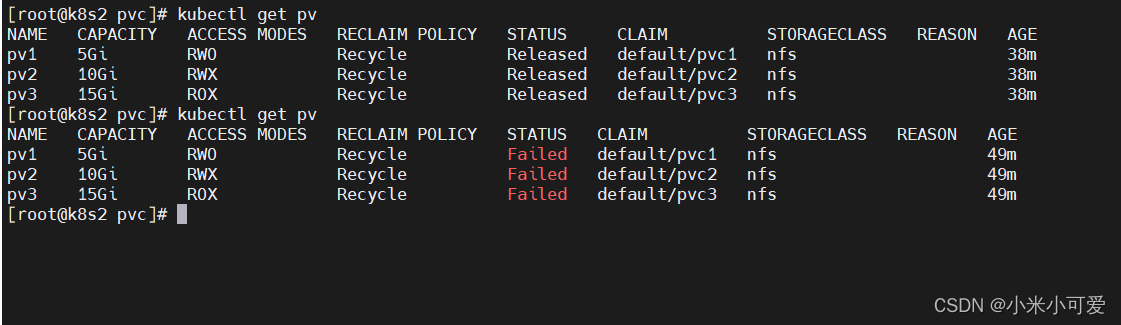
k8s-14 存储之volumes
Volumes配置管理 容器中的文件在磁盘上是临时存放的,这给容器中运行的特殊应用程序带来一些问题。首先,当容器崩溃时,kubelet 将重新启动容器,容器中的文件将会丢失因为容器会以干净的状态重建。其次,当在一个 Pod 中…...
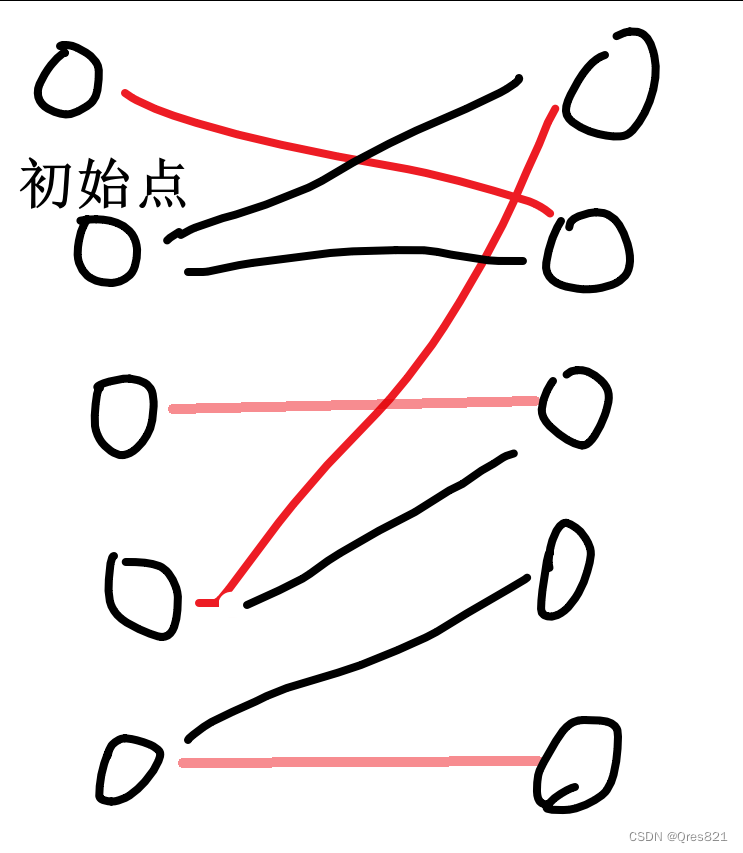
二分图博弈
一张二分图,Alice和Bob每人走一步,不能重复走,谁不能走谁输 结论:若存在最大匹配不包含初始点,则Bob赢,否则Alice赢 以上图为例,红色为最大匹配。 首先对于Alice第一步只能走黑边。而Alice无论…...

【C++】C++11—— 包装器
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C学习 🎯长路漫漫浩浩,万事皆有期待 上一篇博客:【C】C11…...

LED显示屏高刷新率和低刷新率有什么区别
LED显示屏的刷新率是指图像在LED显示屏上更新的速度,也即屏幕上的图像每秒钟出现的次数,它的单位是赫兹(Hz)。LED显示屏的刷新率越高,图像闪烁感就越小,稳定性也就越高,换言之对视力的保护也越好…...

国际伦敦银点差费值得吗?
伦敦银是国际轨技术属市场上广受追捧的白银保证金交易品种,具有交易时长、交易制度灵活、资金利用率高等诸多的优点。 国际伦敦银的优势主要来自它所实行的是保证金交易制度。目前香港平台一般执行的保证金比例标准是2%,以目前22美元/盎司左右的白银价格…...
常见的作物模型应用技巧!DSSAT模型、APSIM模型、WOFOST模型与PCSE模型等应用
①最新DSSAT作物模型建模方法及应用 DSSAT模型内核算法是基于Fortran语言开发的,软件界面是基于C进行开发。了解和熟悉DSSAT模型的关键算法和软件的操作是学习DSSAT模型的基础。此外,想要成为一名优秀的作物模型使用者与科研团队不可或缺的人才ÿ…...
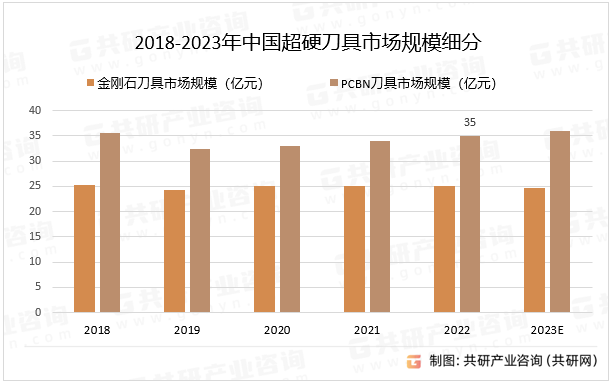
2023年中国超硬材料制品分析及超硬刀具市场规模分析[图]
超硬材料是指硬度特别高的材料,可分为天然以及人造两种,前者主要包括天然的钻石(金刚石)、黑钻石,后者则包括人造金刚石、立方氮化硼。 超硬材料制品分类 资料来源:共研产业咨询(共研网&#x…...

使用React、Express实现一个问卷发布/收集系统
1. 设置项目结构 questionnaire-system/client/ // 前端应用src/components/ // React组件pages/ // 页面App.jsindex.jsserver/ // 后端服务routes/ // 路由models/ // 数据模型app.jspackage.json2. 启动前端应用…...
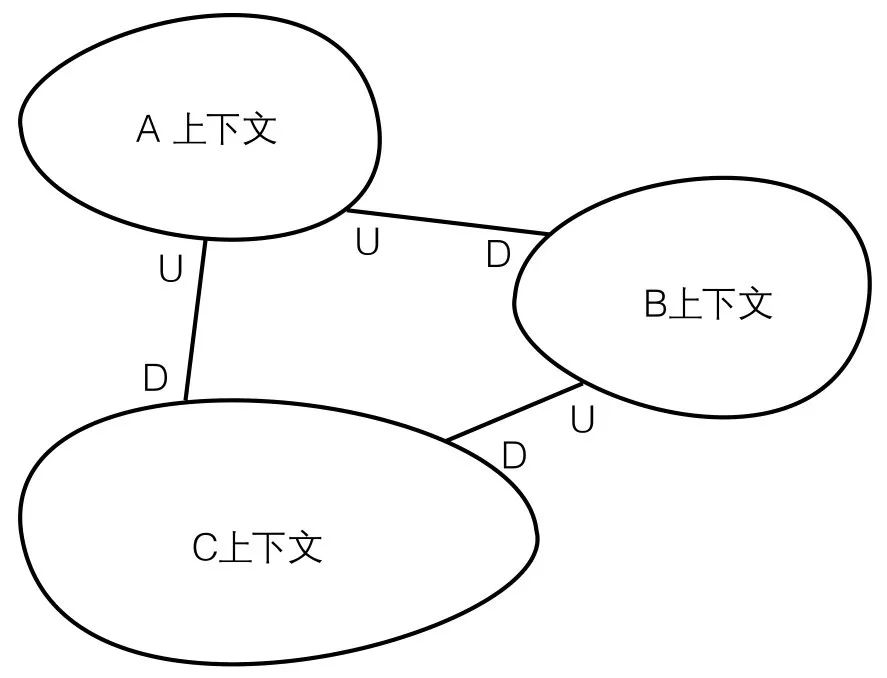
DDD之上下文映射图(Context Mapping)
领域驱动设计系列文章,点击上方合集↑ 1. 开头 在DDD中,限界上下文与限界上下文之间需要相互集成,这种集成关系在DDD中称为上下文映射(Context Mapping),也就是子域与子域之间的集成关系。 所以首先我们…...
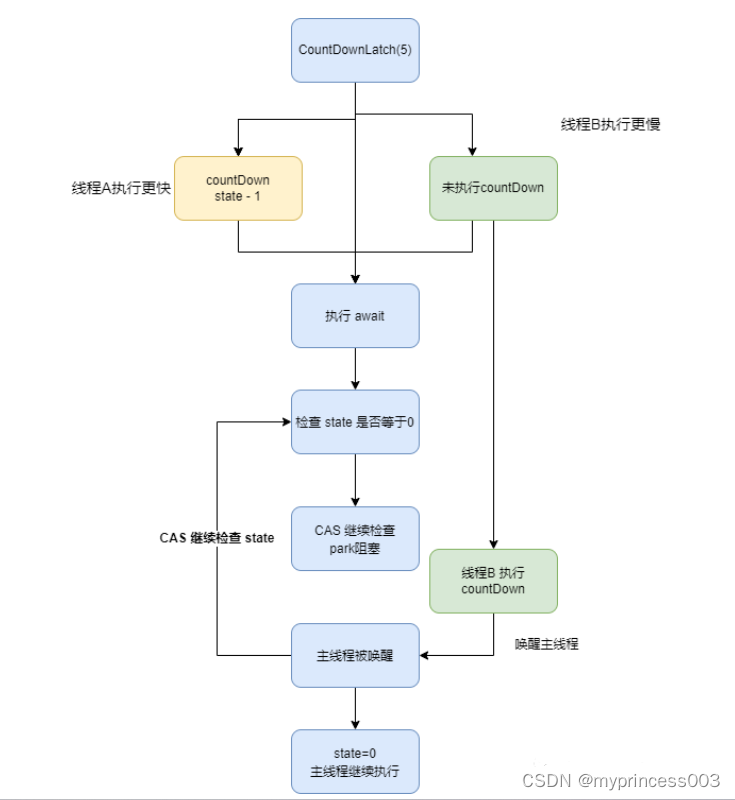
CountDownLatch的原理
使用CountDownLatch可以实现等待多个线程执行完毕的功能,实现线程之间的协调,让它们按照我们期望的顺序执行,从而避免了可能出现的并发问题。 CountDownLatch是如何实现主线程等待子线程全部结束的呢? 代码用例 这里我们使用一段…...

Java新特性Stream流详解
一、概述 Stream流是Java 8 API添加的一个新的抽象,以一种声明性方式处理数据集合(侧重对于源数据计算能力的封装,并且支持序列与并行两种操作方式)。 Stream流是对集合(Collection)对象功能的增强…...

关于VScode中一些常用的快捷操作!
vscode CTRLO:打开文件夹以开始工作 先CTRLK 再CTRLO:打开文件夹以开始工作 如何选择workspace:file → open folder→选目标文件夹【当前工作区选择会影响代码是否能运行】 如何打开终端:View → terminal debug看不到变化历史&…...

Django 使用Mysql数据库
目录 Django 使用Mysql数据库本地安装Mysql数据服务安装好Pymysql服务Django配置数据库迁移各种报错无法找到mysqlclient数据库拒绝连接 Django 使用Mysql数据库 本地安装Mysql数据服务 安装好Pymysql服务 python3 -m pip install PyMySQL官方文档介绍 Django配置 官网文档 …...
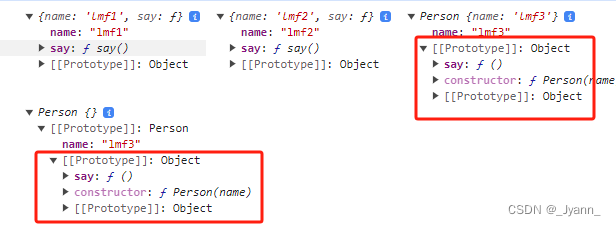
js继承的几种方式(原型链继承、构造函数继承、组合式继承、寄生组合式继承、ES6的Class类继承)
1.原型链继承 实现原理:子类的原型指向父类实例。子类在自身实例上找不到属性和方法时去它父类实例(父类实例和实例的原型对象)上查找,从而实现对父类属性和方法的继承 缺点: 子类创建时不能传参(即没有…...

AnyTransition/过渡动画, MatchedGeometryEffect/匹配几何动画效果 的使用
1. AnyTransition 过渡动画效果 1.1 创建过度动画案例 AnyTransitionBootcamp.swift import SwiftUI/// 旋转修饰 View struct RotateViewModifier :ViewModifier{let rotation: Doublefunc body(content: Content) -> some View {content.rotationEffect(Angle(degrees: r…...
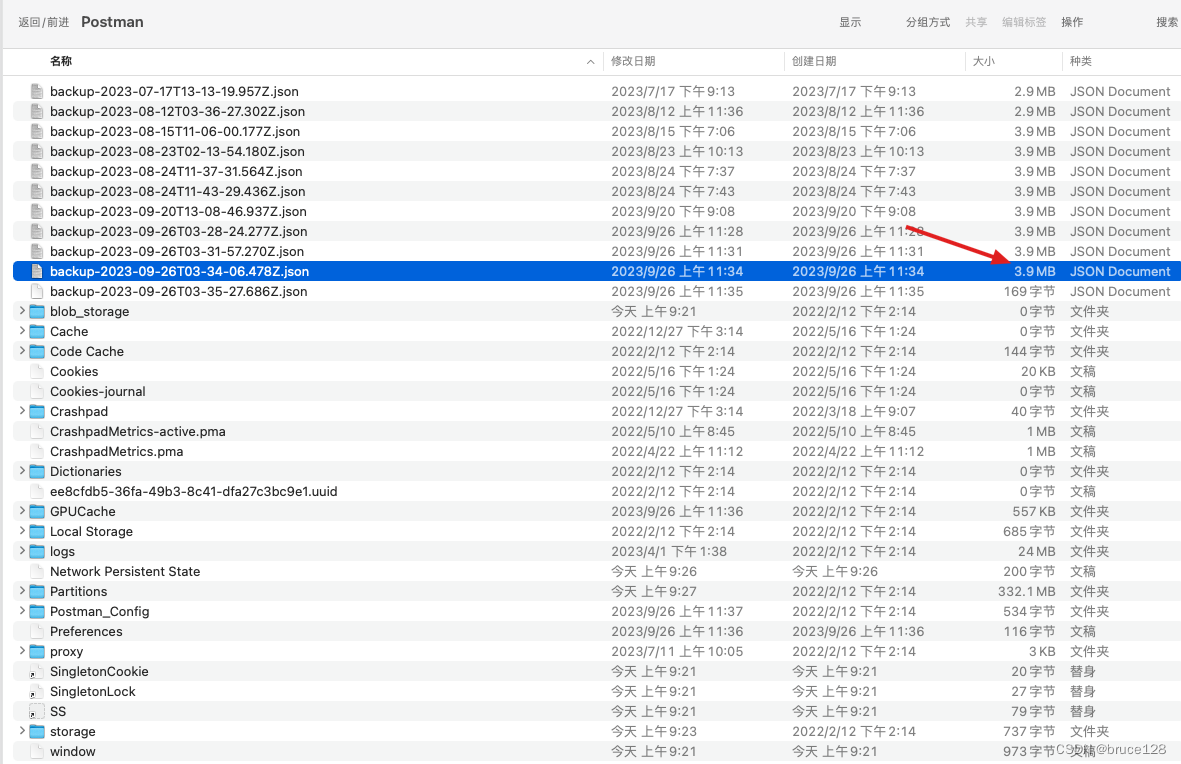
mac版postman升级后数据恢复办法
postman升级了一下,所有的collections都丢失了。 首先在finder里找到这个路径 /Users/{用户名}/Library/Application Support/Postman找到升级之前的的最新的backup.json,然后在postman里import这个文件。 所有升级前的collections都恢复了࿰…...

四.镜头知识之放大倍率
四.镜头知识之放大倍率 文章目录 四.镜头知识之放大倍率4.0 前言4.1 镜头的光学放大倍率的计算方法4.2 显示器的电子放大倍率4.2.1 智能硬件产品的显示放大倍率计算案例4.3 系统放大倍率4.4 智能硬件产品的系统放大倍率计算案例4.4 智能硬件产品的系统放大倍率计算案例4.0 前言…...

Jenkins UI 自动化持续化集成测试
一:安装jenkins 环境 在官网下载msi 直接安装即可 二:设置全局变量 设置allure 路径 三:创建项目 1、创建自由风格项目 2、如果项目在本地,且本地服务器是windows ,找到Jenkins安装根目录,寻找config…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
