OpenFOAM: twoPhaseEulerFoam解读
twoPhaseEulerFoam全解读之一(转载)
本系列将对OpenFOAM-2.1.1 中的 twoPhaseEulerFoam 求解器进行完全解读,共分三部分:方程推导,代码解读,补充说明。本篇进行方程推导,详细介绍如果从双流体模型出发得到 twoPhaseEulerFoam 中的 UEqn.H 对应的模型方程形式。
方程推导
双流体模型方程可以表达成如下形式:
连续性方程:
∂ ( α ϕ ρ ϕ ) ∂ t + ∇ ⋅ ( α ϕ ρ ϕ U ϕ ) = 0 \frac{\partial(\alpha_\phi\rho_\phi)}{\partial t}+\nabla\cdot(\alpha_\phi\rho_\phi U_\phi)=0 ∂t∂(αϕρϕ)+∇⋅(αϕρϕUϕ)=0
动量守恒方程:
∂ ( α ϕ ρ ϕ U ϕ ) ∂ t + ∇ ⋅ ( α ϕ ρ ϕ U ϕ U ϕ ) + ∇ ⋅ ( α ϕ τ ϕ ) + ∇ ⋅ ( α ϕ ρ ϕ R ϕ ) = − α ϕ ∇ p + α ϕ ρ ϕ g + M ϕ \frac{\partial(\alpha_\phi\rho_\phi U_\phi)}{\partial t}+\nabla\cdot(\alpha_\phi\rho_\phi U_\phi U_\phi)+\nabla\cdot(\alpha_\phi\tau_\phi)+\nabla\cdot(\alpha_\phi\rho_\phi R_\phi )=-\alpha_\phi\nabla p+\alpha_\phi\rho_\phi g+M_\phi ∂t∂(αϕρϕUϕ)+∇⋅(αϕρϕUϕUϕ)+∇⋅(αϕτϕ)+∇⋅(αϕρϕRϕ)=−αϕ∇p+αϕρϕg+Mϕ
式中,下标 ϕ = a , b \phi=a,b ϕ=a,b分别代表分散相和连续相, τ ϕ \tau_\phi τϕ表示粘性应力项, R ϕ R_\phi Rϕ表示雷诺应力项, M ϕ M_\phi Mϕ表示相间作用项。
上述方程是完全守恒形式的,但是注意到上述动量方程的瞬变项是 ∂ ( α ϕ ρ ϕ U ϕ ) ∂ t \frac{\partial(\alpha_\phi\rho_\phi U_\phi)}{\partial t} ∂t∂(αϕρϕUϕ),等于说解这个方程能得到的是每个时间步的动量,若要转化成速度,则需要用动量除以密度与体积分率的乘积,即 ( α ϕ ρ ϕ U ϕ ) α ϕ ρ ϕ \frac{(\alpha_\phi\rho_\phi U_\phi)}{\alpha_\phi\rho_\phi} αϕρϕ(αϕρϕUϕ)。那么当离散相a的体积分率 α a → 0 \alpha_a\to0 αa→0时,这个除法就要出问题了。于是,Weller [1] 提出通过构造一种”phase-intensive”形式的动量方程来避开这个问题,见下面的详细推导。
Weller提出的方法的核心是将 α ϕ ρ ϕ \alpha_\phi\rho_\phi αϕρϕ从动量方程的瞬变项中剥离出来,以使动量方程直接对速度进行演化,而不是动量。
首先对动量方程的瞬变项和对流项进行如下转化:
∂ ( α ϕ ρ ϕ U ϕ ) ∂ t = α ϕ ρ ϕ ∂ ( U ϕ ) ∂ t + U ϕ ∂ ( α ϕ ρ ϕ ) ∂ t \frac{\partial(\alpha_\phi\rho_\phi U_\phi)}{\partial t}=\alpha_\phi\rho_\phi\frac{\partial( U_\phi)}{\partial t}+U_\phi\frac{\partial(\alpha_\phi\rho_\phi )}{\partial t} ∂t∂(αϕρϕUϕ)=αϕρϕ∂t∂(Uϕ)+Uϕ∂t∂(αϕρϕ)
∇ ⋅ ( α ϕ ρ ϕ U ϕ U ϕ ) = α ϕ ρ ϕ U ϕ ⋅ ∇ ( U ϕ ) + U ϕ ∇ ⋅ ( α ϕ ρ ϕ U ϕ ) \nabla\cdot(\alpha_\phi\rho_\phi U_\phi U_\phi)= \alpha_\phi\rho_\phi U_\phi\cdot \nabla( U_\phi) + U_\phi\nabla\cdot(\alpha_\phi\rho_\phi U_\phi) ∇⋅(αϕρϕUϕUϕ)=αϕρϕUϕ⋅∇(Uϕ)+Uϕ∇⋅(αϕρϕUϕ)
注:这里到了张量运算公式 [ ∇ ⋅ v w ] = [ v ⋅ ∇ w ] + w ( ∇ ⋅ v ) [\nabla\cdot \mathbf{vw}]=[\mathbf{v}\cdot\nabla\mathbf{w}]+\mathbf{w}(\nabla\cdot\mathbf{v}) [∇⋅vw]=[v⋅∇w]+w(∇⋅v),具体可参考 Bird 的 Transport Phenomenon 的 Appendix A。
于是,瞬变项和对流项的加和可以写成如下形式:
∂ ( α ϕ ρ ϕ U ϕ ) ∂ t + ∇ ⋅ ( α ϕ ρ ϕ U ϕ U ϕ ) = α ϕ ρ ϕ [ ∂ ( U ϕ ) ∂ t + U ϕ ⋅ ∇ ( U ϕ ) ] + U ϕ [ ∂ ( α ϕ ρ ϕ ) ∂ t + ∇ ⋅ ( α ϕ ρ ϕ U ϕ ) ] \frac{\partial(\alpha_\phi\rho_\phi U_\phi)}{\partial t}+\nabla\cdot(\alpha_\phi\rho_\phi U_\phi U_\phi)=\alpha_\phi\rho_\phi\left[\frac{\partial( U_\phi)}{\partial t}+U_\phi \cdot \nabla( U_\phi)\right]+U_\phi \left[ \frac{\partial(\alpha_\phi\rho_\phi )}{\partial t}+\nabla\cdot(\alpha_\phi\rho_\phi U_\phi)\right] ∂t∂(αϕρϕUϕ)+∇⋅(αϕρϕUϕUϕ)=αϕρϕ[∂t∂(Uϕ)+Uϕ⋅∇(Uϕ)]+Uϕ[∂t∂(αϕρϕ)+∇⋅(αϕρϕUϕ)]
注意右边第二项的括号里其实就是连续性方程的左边,其值为0,因此得到:
∂ ( α ϕ ρ ϕ U ϕ ) ∂ t + ∇ ⋅ ( α ϕ ρ ϕ U ϕ U ϕ ) = α ϕ ρ ϕ [ ∂ ( U ϕ ) ∂ t + U ϕ ⋅ ∇ ( U ϕ ) ] \frac{\partial(\alpha_\phi\rho_\phi U_\phi)}{\partial t}+\nabla\cdot(\alpha_\phi\rho_\phi U_\phi U_\phi) = \alpha_\phi\rho_\phi\left[\frac{\partial( U_\phi)}{\partial t}+U_\phi \cdot \nabla( U_\phi)\right] ∂t∂(αϕρϕUϕ)+∇⋅(αϕρϕUϕUϕ)=αϕρϕ[∂t∂(Uϕ)+Uϕ⋅∇(Uϕ)]
于是得到第一步转化之后的动量方程:
α ϕ ρ ϕ [ ∂ ( U ϕ ) ∂ t + U ϕ ⋅ ∇ ( U ϕ ) ] + ∇ ⋅ ( α ϕ τ ϕ ) + ∇ ⋅ ( α ϕ ρ ϕ R ϕ ) = − α ϕ ∇ p + α ϕ ρ ϕ g + M ϕ \alpha_\phi\rho_\phi\left[\frac{\partial( U_\phi)}{\partial t}+U_\phi\cdot\nabla( U_\phi)\right] + \nabla\cdot(\alpha_\phi\tau_\phi) + \nabla\cdot(\alpha_\phi\rho_\phi R_\phi ) = -\alpha_\phi\nabla p + \alpha_\phi\rho_\phi g + M_\phi αϕρϕ[∂t∂(Uϕ)+Uϕ⋅∇(Uϕ)]+∇⋅(αϕτϕ)+∇⋅(αϕρϕRϕ)=−αϕ∇p+αϕρϕg+Mϕ
下面处理粘性应力项和雷诺应力项。
∇ ⋅ ( α ϕ τ ϕ ) + ∇ ⋅ ( α ϕ ρ ϕ R ϕ ) = ∇ ⋅ [ α ϕ ρ ϕ ( τ ϕ ρ ϕ + R ϕ ) ] = ∇ ⋅ [ α ϕ ρ ϕ R e f f , ϕ ] \nabla\cdot(\alpha_\phi\tau_\phi) + \nabla\cdot(\alpha_\phi\rho_\phi R_\phi )=\nabla\cdot\left[\alpha_\phi\rho_\phi(\frac{\tau_\phi}{\rho_\phi}+R_\phi)\right] = \nabla\cdot\left[\alpha_\phi\rho_\phi R_{eff,\phi}\right ] ∇⋅(αϕτϕ)+∇⋅(αϕρϕRϕ)=∇⋅[αϕρϕ(ρϕτϕ+Rϕ)]=∇⋅[αϕρϕReff,ϕ]
其中 R e f f , ϕ = τ ϕ ρ ϕ + R ϕ R_{eff,\phi}=\frac{\tau_\phi}{\rho_\phi}+R_\phi Reff,ϕ=ρϕτϕ+Rϕ。
根据定义(此处参考BubbleFoam的Wiki页面):
τ ϕ = − ρ ϕ ν ϕ [ ∇ U ϕ + ∇ T U ϕ ] + 2 3 ρ ϕ ν ϕ ( ∇ ⋅ U ϕ ) I \boldsymbol{\tau}_{\phi} = - \rho_{\phi} \nu_{\phi} \left[\nabla \mathbf{U}_{\phi} + \nabla^{\textrm{T}} \mathbf{U}_{\phi} \right] + \frac{2}{3}\rho_{\phi}\nu_{\phi} \left( \nabla \cdot \mathbf{U}_{\phi} \right) \mathbf{I} τϕ=−ρϕνϕ[∇Uϕ+∇TUϕ]+32ρϕνϕ(∇⋅Uϕ)I
以及
R ϕ = − ν ϕ , t [ ∇ U ϕ + ∇ T U ϕ ] + 2 3 ν ϕ , t ( ∇ ⋅ U ϕ ) I + 2 3 k ϕ I \mathbf{R}_{\phi} = - \nu_{\phi,\textrm{t}} \left[ \nabla \mathbf{U}_{\phi} +\nabla^{\textrm{T}} \mathbf{U}_{\phi} \right] + \frac{2}{3} \nu_{\phi,\textrm{t}} \left( \nabla \cdot \mathbf{U}_{\phi} \right) \mathbf{I} + \frac{2}{3} k_{\phi} \mathbf{I} Rϕ=−νϕ,t[∇Uϕ+∇TUϕ]+32νϕ,t(∇⋅Uϕ)I+32kϕI
代入到 R e f f , ϕ R_{eff,\phi} Reff,ϕ中,得:
R e f f , ϕ = − ( ν ϕ + ν ϕ , t ) [ ∇ U ϕ + ∇ T U ϕ ] + 2 3 ( ν ϕ + ν ϕ , t ) ( ∇ ⋅ U ϕ ) I + 2 3 k ϕ I R_{eff,\phi}=-(\nu_\phi+\nu_{\phi , t})\left[ \nabla \mathbf{U}_{\phi} +\nabla^{\textrm{T}} \mathbf{U}_{\phi} \right]+\frac{2}{3}(\nu_\phi+\nu_{\phi , t}) \left (\nabla \cdot \mathbf{U}_{\phi}\right ) \mathbf{I} + \frac{2}{3} k_{\phi} \mathbf{I} Reff,ϕ=−(νϕ+νϕ,t)[∇Uϕ+∇TUϕ]+32(νϕ+νϕ,t)(∇⋅Uϕ)I+32kϕI
令 ν e f f = ν ϕ + ν ϕ , t \nu_{eff}=\nu_\phi+\nu_{\phi , t} νeff=νϕ+νϕ,t ,则:
R e f f , ϕ = − ν e f f [ ∇ U ϕ + ∇ T U ϕ ] + 2 3 ν e f f ( ∇ ⋅ U ϕ ) I + 2 3 k ϕ I = − ν e f f ∇ U ϕ + R c , ϕ R_{eff,\phi}=-\nu_{eff}\left[ \nabla \mathbf{U}_{\phi} +\nabla^{\textrm{T}} \mathbf{U}_{\phi} \right]+\frac{2}{3}\nu_{eff} \left (\nabla \cdot \mathbf{U}_{\phi}\right ) \mathbf{I} + \frac{2}{3} k_{\phi} \mathbf{I} = -\nu_{eff}\nabla U_\phi + R_{c,\phi} Reff,ϕ=−νeff[∇Uϕ+∇TUϕ]+32νeff(∇⋅Uϕ)I+32kϕI=−νeff∇Uϕ+Rc,ϕ
其中 R c , ϕ = − ν e f f ∇ U ϕ T + 2 3 ν e f f ( ∇ ⋅ U ϕ ) I + 2 3 k ϕ I R_{c,\phi}=-\nu_{eff} \nabla \mathbf{U}^\textrm{T}_{\phi}+\frac{2}{3}\nu_{eff} \left (\nabla \cdot \mathbf{U}_{\phi}\right ) \mathbf{I} + \frac{2}{3} k_{\phi} \mathbf{I} Rc,ϕ=−νeff∇UϕT+32νeff(∇⋅Uϕ)I+32kϕI
于是得到:
∇ ⋅ [ α ϕ ρ ϕ R e f f , ϕ ] = ∇ ( α ϕ ρ ϕ ) ⋅ [ R e f f , ϕ ] + α ϕ ρ ϕ ∇ ⋅ [ R e f f , ϕ ] = α ϕ ρ ϕ ∇ ⋅ [ − ν e f f ∇ U ϕ ] + α ϕ ρ ϕ ∇ ⋅ [ R c , ϕ ] + ∇ ( α ϕ ρ ϕ ) [ − ν e f f ∇ U ϕ + R c , ϕ ] \begin{aligned} \nabla\cdot\left[\alpha_\phi\rho_\phi R_{eff,\phi}\right ] = & \nabla(\alpha_\phi\rho_\phi)\cdot\left[ R_{eff,\phi}\right] + \alpha_\phi\rho_\phi\nabla\cdot \left [ R_{eff,\phi}\right ]\\ =& \alpha_\phi\rho_\phi\nabla\cdot\left[ -\nu_{eff}\nabla U_\phi\right] + \alpha_\phi\rho_\phi\nabla\cdot\left[ R_{c,\phi}\right] + \nabla(\alpha_\phi\rho_\phi)\left[ -\nu_{eff}\nabla U_\phi + R_{c,\phi}\right] \end{aligned} ∇⋅[αϕρϕReff,ϕ]==∇(αϕρϕ)⋅[Reff,ϕ]+αϕρϕ∇⋅[Reff,ϕ]αϕρϕ∇⋅[−νeff∇Uϕ]+αϕρϕ∇⋅[Rc,ϕ]+∇(αϕρϕ)[−νeff∇Uϕ+Rc,ϕ]
代入到动量方程中,并且方程两边同时除以 α ϕ ρ ϕ \alpha_\phi\rho_\phi αϕρϕ,得到:
∂ U ϕ ∂ t + U ϕ ⋅ ∇ U ϕ − ∇ ⋅ [ ν e f f ∇ U ϕ ] + ∇ ⋅ [ R c , ϕ ] + ∇ ( α ϕ ρ ϕ ) α ϕ ρ ϕ ⋅ [ − ν e f f ∇ U ϕ + R c , ϕ ] = − ∇ p ρ ϕ + g + M ϕ α ϕ ρ ϕ \frac{\partial U_\phi}{\partial t} + U_\phi\cdot\nabla U_\phi -\nabla \cdot \left[ \nu_{eff} \nabla U_\phi \right ] + \nabla \cdot \left[ R_{c,\phi}\right] + \frac{\nabla(\alpha_\phi\rho_\phi)}{\alpha_\phi\rho_\phi}\cdot \left[ -\nu_{eff}\nabla U_\phi + R_{c,\phi}\right] = -\frac{\nabla p}{\rho_\phi} + g + \frac{M_\phi}{\alpha_\phi\rho_\phi} ∂t∂Uϕ+Uϕ⋅∇Uϕ−∇⋅[νeff∇Uϕ]+∇⋅[Rc,ϕ]+αϕρϕ∇(αϕρϕ)⋅[−νeff∇Uϕ+Rc,ϕ]=−ρϕ∇p+g+αϕρϕMϕ
如果假定两相流体均为不可压缩,密度恒为常数,于是可以得到不可压缩的双流体模型的方程组:
连续性方程
∂ ( α ϕ ) ∂ t + ∇ ⋅ ( α ϕ U ϕ ) = 0 \frac{\partial(\alpha_\phi)}{\partial t}+\nabla\cdot(\alpha_\phi U_\phi)=0 ∂t∂(αϕ)+∇⋅(αϕUϕ)=0
动量方程
∂ U ϕ ∂ t + U ϕ ⋅ ∇ U ϕ − ∇ ⋅ [ ν e f f ∇ U ϕ ] + ∇ ⋅ [ R c , ϕ ] + ∇ ( α ϕ ) α ϕ ⋅ [ − ν e f f ∇ U ϕ + R c , ϕ ] = − ∇ p ρ ϕ + g + M ϕ α ϕ ρ ϕ \frac{\partial U_\phi}{\partial t} + U_\phi\cdot\nabla U_\phi -\nabla \cdot \left[ \nu_{eff} \nabla U_\phi \right ] + \nabla \cdot \left[ R_{c,\phi}\right] + \frac{\nabla(\alpha_\phi)}{\alpha_\phi} \cdot \left[ -\nu_{eff}\nabla U_\phi + R_{c,\phi}\right] = -\frac{\nabla p}{\rho_\phi} + g + \frac{M_\phi}{\alpha_\phi\rho_\phi} ∂t∂Uϕ+Uϕ⋅∇Uϕ−∇⋅[νeff∇Uϕ]+∇⋅[Rc,ϕ]+αϕ∇(αϕ)⋅[−νeff∇Uϕ+Rc,ϕ]=−ρϕ∇p+g+αϕρϕMϕ
方程中还剩下相间作用项没有处理,对于分散相和连续项形式,相间作用力是大小相等符号想反,这里只考虑分散相的形式,令 ϕ = a \phi=a ϕ=a,则得到分散相的动量方程:
∂ U a ∂ t + U a ⋅ ∇ U a − ∇ ⋅ [ ν e f f ∇ U a ] + ∇ ⋅ [ R c , a ] + ∇ ( α a ) α a ⋅ [ − ν e f f ∇ U a + R c , a ] = − ∇ p ρ a + g + M a α a ρ a \frac{\partial U_a}{\partial t} + U_a\cdot\nabla U_a -\nabla \cdot \left[ \nu_{eff} \nabla U_a \right ] + \nabla \cdot \left[ R_{c,a}\right] + \frac{\nabla(\alpha_a)}{\alpha_a} \cdot \left[ -\nu_{eff}\nabla U_a + R_{c,a}\right] = -\frac{\nabla p}{\rho_a} + g + \frac{M_a}{\alpha_a\rho_a} ∂t∂Ua+Ua⋅∇Ua−∇⋅[νeff∇Ua]+∇⋅[Rc,a]+αa∇(αa)⋅[−νeff∇Ua+Rc,a]=−ρa∇p+g+αaρaMa
相间作用只考虑曳力,升力以及虚拟质量力,即 M , a = M d r a g + M l i f t + M v m M,a=M_{drag}+M_{lift}+M_{vm} M,a=Mdrag+Mlift+Mvm,下面分别考虑每一种相间作用力。
曳力
M d r a g = − β ( U a − U b ) M_{drag}=-\beta(U_a-U_b) Mdrag=−β(Ua−Ub),其中 β \beta β为曳力系数。
升力
M l i f t = − α a α b C l ( α b ρ b + α a ρ a ) U r × ( ∇ × U ) M_{lift}=-\alpha_a\alpha_b C_l (\alpha_b \rho_b + \alpha_a \rho_a)U_r \times (\nabla \times U) Mlift=−αaαbCl(αbρb+αaρa)Ur×(∇×U) ,其中 U r = U a − U b U_r=U_a-U_b Ur=Ua−Ub, U = α a U a + α b U b U=\alpha_a U_a + \alpha_b U_b U=αaUa+αbUb
虚拟质量力
M v m = α a α b C v m ρ b [ D U b D t − D U a D t ] M_{vm}=\alpha_a\alpha_b C_{vm}\rho_b\left[ \frac{DU_b}{Dt}-\frac{DU_a}{Dt}\right] Mvm=αaαbCvmρb[DtDUb−DtDUa],其中 D D t \frac{D}{Dt} DtD表示物质导数, D U b D t = ∂ U b ∂ t + U b ⋅ ∇ U b \frac{DU_b}{Dt}=\frac{\partial U_b}{\partial t} + U_b \cdot \nabla U_b DtDUb=∂t∂Ub+Ub⋅∇Ub, D U a D t = ∂ U a ∂ t + U a ⋅ ∇ U a \frac{DU_a}{Dt}=\frac{\partial U_a}{\partial t}+U_a \cdot \nabla U_a DtDUa=∂t∂Ua+Ua⋅∇Ua
考虑到形式的统一,令 K = β α a α b K=\frac{\beta}{\alpha_a\alpha_b} K=αaαbβ,则曳力可表示为 M d r a g = − α a α b K ( U a − U b ) M_{drag}=-\alpha_a\alpha_b K(U_a-U_b) Mdrag=−αaαbK(Ua−Ub)
代入到分散相a的动量方程中,得到:
∂ U a ∂ t + U a ⋅ ∇ U a − ∇ ⋅ [ ν e f f ∇ U a ] + ∇ ⋅ [ R c , a ] + ∇ ( α a ) α a ⋅ [ − ν e f f ∇ U a + R c , a ] = − ∇ p ρ a + g − α b ρ a K ( U a − U b ) − α b ρ a C l ( α b ρ b + α a ρ a ) U r × ( ∇ × U ) + α b ρ a C v m ρ b [ ∂ U b ∂ t + U b ⋅ ∇ U b − ( ∂ U a ∂ t + U a ⋅ ∇ U a ) ] \begin{aligned} &\frac{\partial U_a}{\partial t} + U_a\cdot \nabla U_a -\nabla \cdot \left[ \nu_{eff} \nabla U_a \right ] + \nabla \cdot \left[ R_{c,a}\right] + \frac{\nabla(\alpha_a)}{\alpha_a} \cdot \left[ -\nu_{eff}\nabla U_a + R_{c,a}\right] \\ = & -\frac{\nabla p}{\rho_a} + g - \frac{\alpha_b}{\rho_a} K (U_a-U_b) - \frac{\alpha_b}{\rho_a} C_l (\alpha_b \rho_b + \alpha_a \rho_a) U_r \times (\nabla \times U) \\ +& \frac{\alpha_b}{\rho_a} C_{vm}\rho_b\left[ \frac{\partial U_b}{\partial t} + U_b \cdot \nabla U_b - (\frac{\partial U_a}{\partial t}+U_a \cdot \nabla U_a)\right] \end{aligned} =+∂t∂Ua+Ua⋅∇Ua−∇⋅[νeff∇Ua]+∇⋅[Rc,a]+αa∇(αa)⋅[−νeff∇Ua+Rc,a]−ρa∇p+g−ρaαbK(Ua−Ub)−ρaαbCl(αbρb+αaρa)Ur×(∇×U)ρaαbCvmρb[∂t∂Ub+Ub⋅∇Ub−(∂t∂Ua+Ua⋅∇Ua)]
将相关的项合并,并调整顺序,便得到与twoPhaseEulerFoam求解器的UEqn.H文件中相同形式的分散相动量方程:
( 1 + α b ρ b ρ a C v m ) ( ∂ U a ∂ t + U a ⋅ ∇ U a ) − ∇ ⋅ [ ν e f f ∇ U a ] + ∇ ⋅ [ R c , a ] + ∇ ( α a ) α a ⋅ [ − ν e f f ∇ U a + R c , a ] = − α b ρ a K U a − α b ρ a { C l ( α b ρ b + α a ρ a ) U r × ( ∇ × U ) − C v m ρ b [ ∂ U b ∂ t + U b ⋅ ∇ U b ] } − ∇ p ρ a + g + α b ρ a K U b \begin{aligned} &(1+\frac{\alpha_b \rho_b}{\rho_a} C_{vm})(\frac{\partial U_a}{\partial t} + U_a\cdot \nabla U_a ) -\nabla \cdot \left[ \nu_{eff} \nabla U_a \right ] + \nabla \cdot \left[ R_{c,a}\right] + \frac{\nabla(\alpha_a)}{\alpha_a} \cdot \left[ -\nu_{eff}\nabla U_a + R_{c,a}\right] \\ = & -\frac{\alpha_b}{\rho_a} K U_a - \frac{\alpha_b}{\rho_a} \left\{ {C_l (\alpha_b \rho_b + \alpha_a \rho_a) U_r \times (\nabla \times U) - C_{vm}\rho_b\left[ {\frac{\partial U_b}{\partial t} + U_b \cdot \nabla U_b }\right] } \right\} \\ &- \frac{\nabla p}{\rho_a} + g + \frac{\alpha_b}{\rho_a} K U_b \end{aligned} =(1+ρaαbρbCvm)(∂t∂Ua+Ua⋅∇Ua)−∇⋅[νeff∇Ua]+∇⋅[Rc,a]+αa∇(αa)⋅[−νeff∇Ua+Rc,a]−ρaαbKUa−ρaαb{Cl(αbρb+αaρa)Ur×(∇×U)−Cvmρb[∂t∂Ub+Ub⋅∇Ub]}−ρa∇p+g+ρaαbKUb
连续相b的动量方程形式相仿,这里就不再重复了。这里有几点注意事项:
此处的双流体模型在推导的过程中,是把a当作分散相,b当作连续相的。分散相的体积分率 α a \alpha_a αa可以等于0,但是连续项体积分率 α b \alpha_b αb不能等于0 ,否则会出问题。
曳力系数 β \beta β 的形式就是文献中常见的形式,比如,WenYu 曳力系数 β = 3 4 ( 1 − α b ) α b d p , a ∣ U b − U a ∣ C D 0 α b − 2.7 \beta=\frac{3}{4}\frac{(1-\alpha_b)\alpha_b}{d_{p,a}}|U_b-U_a|C_{D0}\alpha_b^{-2.7} β=43dp,a(1−αb)αb∣Ub−Ua∣CD0αb−2.7,Ergun 曳力系数 β = 150 ( 1 − α b ) 2 μ b α b d a 2 + 1.75 ( 1 − α b ) ρ b U b − U a d a \beta=150\frac{(1-\alpha_b)^2\mu_b}{\alpha_b d_a^2}+1.75\frac{(1-\alpha_b)\rho_b{U_b-U_a}}{d_a} β=150αbda2(1−αb)2μb+1.75da(1−αb)ρbUb−Ua。而程序中定义的 K = β α a α b K=\frac{\beta}{\alpha_a\alpha_b} K=αaαbβ,所以,当 α b → 0 \alpha_b\to 0 αb→0时,如果用WenYu曳力那还不会出错,因为曳力系数中的分子里同时含有 α a α b \alpha_a\alpha_b αaαb,运算 K = β α a α b K=\frac{\beta}{\alpha_a\alpha_b} K=αaαbβ不会出现除以0的问题;但如果用Ergun曳力,那就要出问题了,因为Ergun曳力系数中两项的分子都没有 α b \alpha_b αb,所以运算 K = β α a α b K=\frac{\beta}{\alpha_a\alpha_b} K=αaαbβ就要出问题了。
相关文章:

OpenFOAM: twoPhaseEulerFoam解读
twoPhaseEulerFoam全解读之一(转载) 本系列将对OpenFOAM-2.1.1 中的 twoPhaseEulerFoam 求解器进行完全解读,共分三部分:方程推导,代码解读,补充说明。本篇进行方程推导,详细介绍如果从双流体模型出发得到 twoPhaseEu…...

ffmpeg跨平台arm编译-ubuntu
目录 1. 安装必要的编译器2. 安装必要的依赖项3. 配置编译选项4. 编译安装 1. 安装必要的编译器 32位系统: sudo apt-get update sudo apt-get install gcc-arm-linux-gnueabihf sudo apt-get install g-arm-linux-gnueabihf64位系统: sudo apt-get u…...

Vue 网络处理 - axios 异步请求的使用,请求响应拦截器
目录 一、axiox 1.1、axios 简介 1.2、axios 基本使用 1.2.1、下载核心 js 文件. 1.2.2、发送 GET 异步请求 1.2.3、发送 POST 异步请求 1.2.4、发送 GET、POST 请求最佳实践 1.3、请求响应拦截器 1.3.1、拦截器解释 1.3.2、请求拦截器的使用 1.3.3、响应拦截器的使用…...

单目3D目标检测——MonoDLE 模型训练 | 模型推理
本文分享 MonoDLE 的模型训练、模型推理、可视化3D检测结果。 模型原理,参考我这篇博客:【论文解读】单目3D目标检测 MonoDLE(CVPR2021)_一颗小树x的博客-CSDN博客 源码地址:https://github.com/xinzhuma/monodle 目…...

CSS悬停卡片翻转明信片效果源码附注释
运行效果演示: HTML页面代码: <!DOCTYPE html> <html lang="en" > <head>...
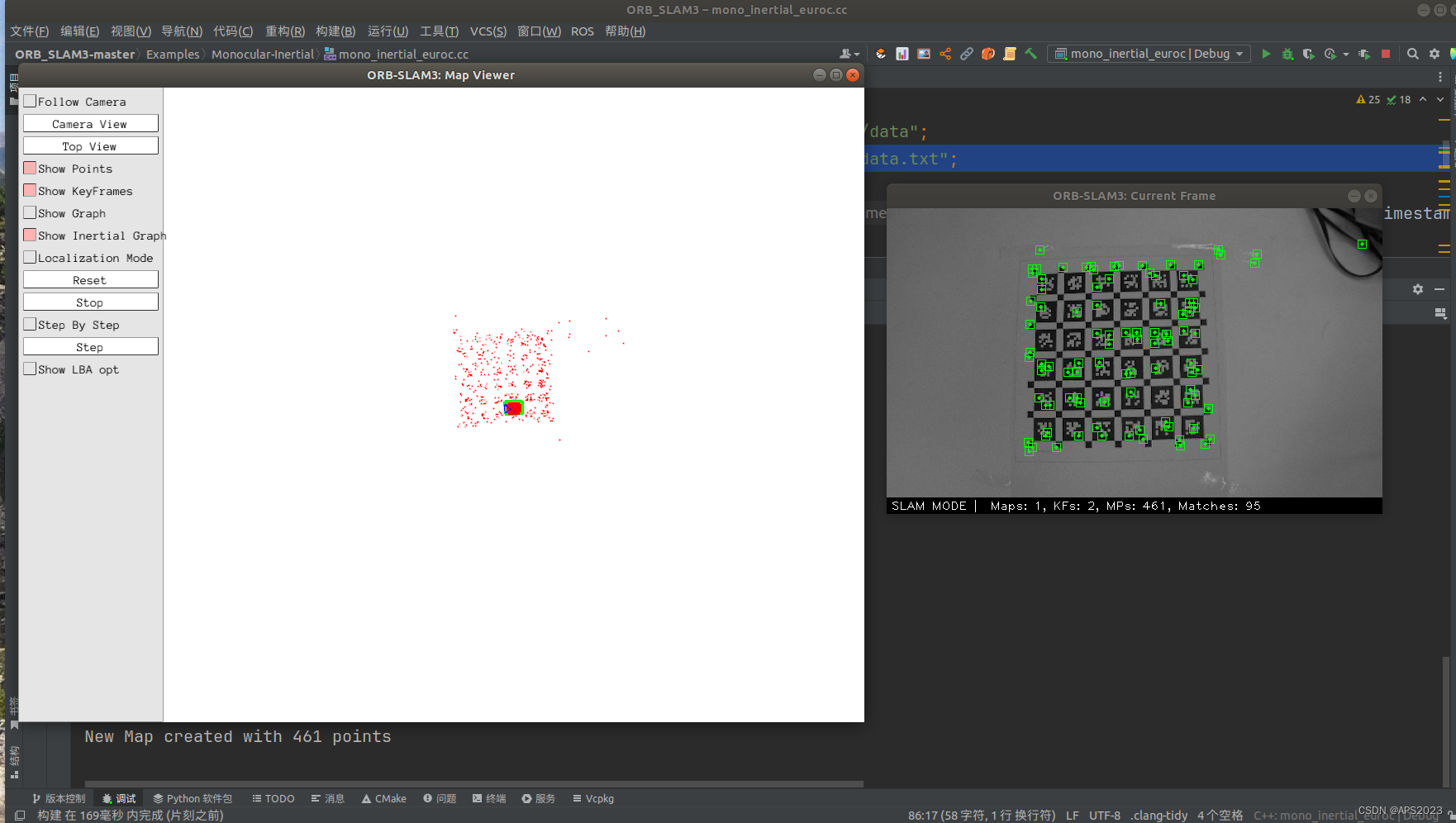
使用kaliber与imu_utils进行IMU、相机+IMU联合标定
目录 1 标定工具编译 1.1 IMU标定工具 imu_utils 1.2 相机标定工具 kaliber 2 标定数据录制 3 开始标定 3.1 IMU标定 3.2 相机标定 3.3 相机IMU联合标定 4 将参数填入ORBSLAM的文件中 1 标定工具编译 1.1 IMU标定工具 imu_utils 标定IMU我们使用imu_utils软件进行标定…...

统一观测丨使用 Prometheus 监控 SQL Server 最佳实践
作者:啃唯 SQL Server 简介 SQL Server 是什么? Microsoft SQL Server 是 Microsoft 推出的关系型数据库解决方案,支持企业 IT 环境中的各种事务处理、商业智能和分析应用程序。Microsoft SQL Server 是市场领先的数据库技术之一。 SQL S…...
最短无序连续子数组
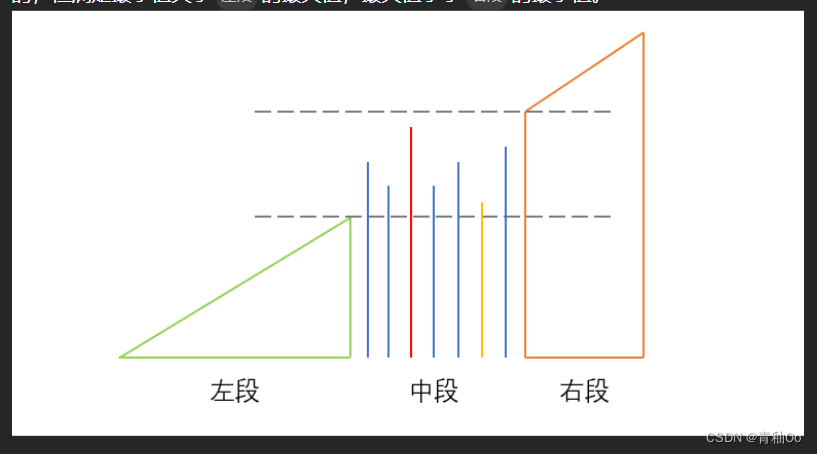
题目链接 最短无序连续子数组 题目描述 注意点 找出符合题意的 最短 子数组,并输出它的长度-100000 < nums[i] < 100000 解答思路 本题的数组可以分为三段,左段中段和右段,如下图所示 观察规律可知,左段元素始终比中段…...

更新 | 持续开源迅为RK3568驱动指南第十二篇-GPIO子系统
《iTOP-RK3568开发板驱动开发指南》更新,本次更新内容对应的是驱动(第十二期_GPIO子系统-全新升级)视频,后续资料会不断更新,不断完善,帮助用户快速入门,大大提升研发速度。 文档教程更新至第十…...
centos7安装erlang23.3.4.11及rabbitmq3.9.16版本
rpm包有系统版本要求,el是Red Hat Enterprise Linux(EL)的缩写。 EL7是Red Hat 7.x,Centos 7.x EL8是Red Hat 8.x, Centos 8.x 所以我们在安装erlang及rabbitmq时需要选择与自己的服务器相对应的rpm包 # rabbitmq的rpm安装包 https://github.com/rabbi…...
VMware和Debian下载
文章目录 ⭐️写在前面的话⭐️一、VMware二、Debain三、建立虚拟机🚀 先看后赞,养成习惯!🚀🚀 先看后赞,养成习惯!🚀 ⭐️写在前面的话⭐️ CSDN主页:程序员好冰 目前在…...

mysql面试题48:MySQL中 Innodb的事务与日志的实现方式
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官: Innodb的事务与日志的实现方式 以下是InnoDB事务和日志的实现方式的详细说明: 事务日志(Transaction Log): InnoDB使用事务日志来保证事务的…...
数据结构 优先级队列(堆)
数据结构 优先级队列(堆) 文章目录 数据结构 优先级队列(堆)1. 优先级队列1.1 概念 2. 优先级队列的模拟实现2.1 堆的概念2.2 堆的存储方式2.3 堆的创建2.3.1 堆向下调整2.3.2 堆的创建2.3.3 建堆的时间复杂度 2.4 堆的插入与删除2.4.1 堆的插入2.4.2 堆的删除 2.5 用堆模拟实现…...

如何在edge浏览器中给PDF添加文字批注
我用的edge浏览器是目前最新版的(一般自动更新到最新版) 最近,我喜欢用edge浏览器查看PDF,节省电脑资源,快捷且方便。 但edge对PDF的标注种类较少,主要是划线和涂色,文字批注功能尚未出现在工具…...
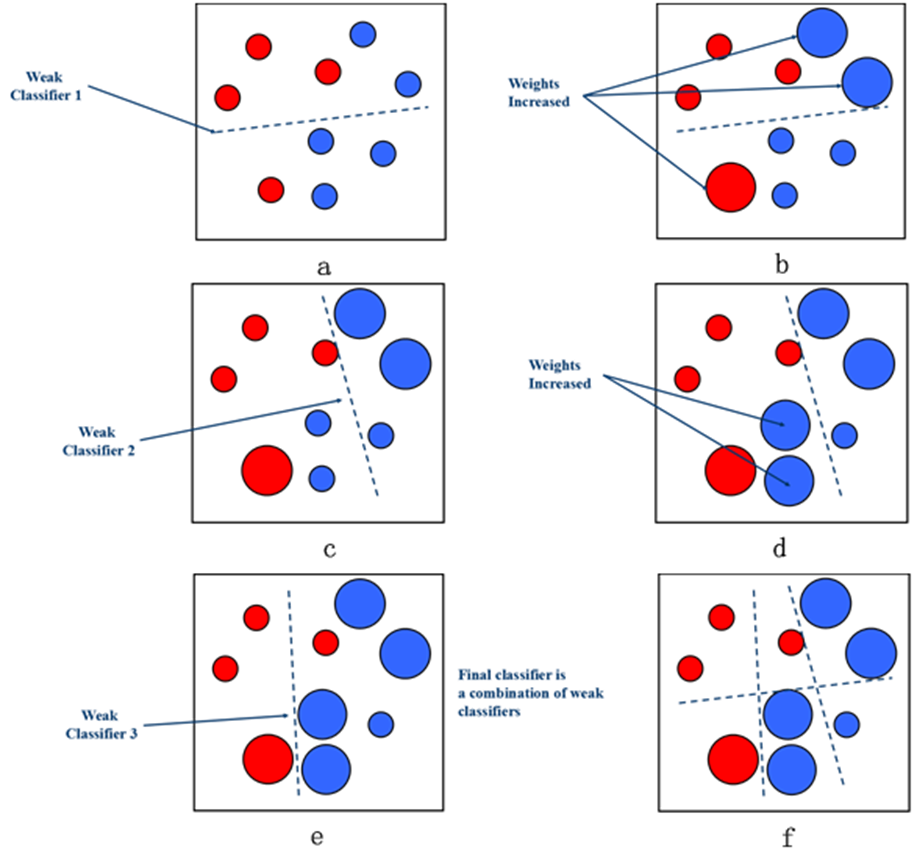
集成学习的小九九
集成学习(Ensemble Learning)是一种机器学习的方法,通过结合多个基本模型的预测结果来进行决策或预测。集成学习的目标是通过组合多个模型的优势,并弥补单个模型的不足,从而提高整体性能。 集成学习的主要策略 在集成…...
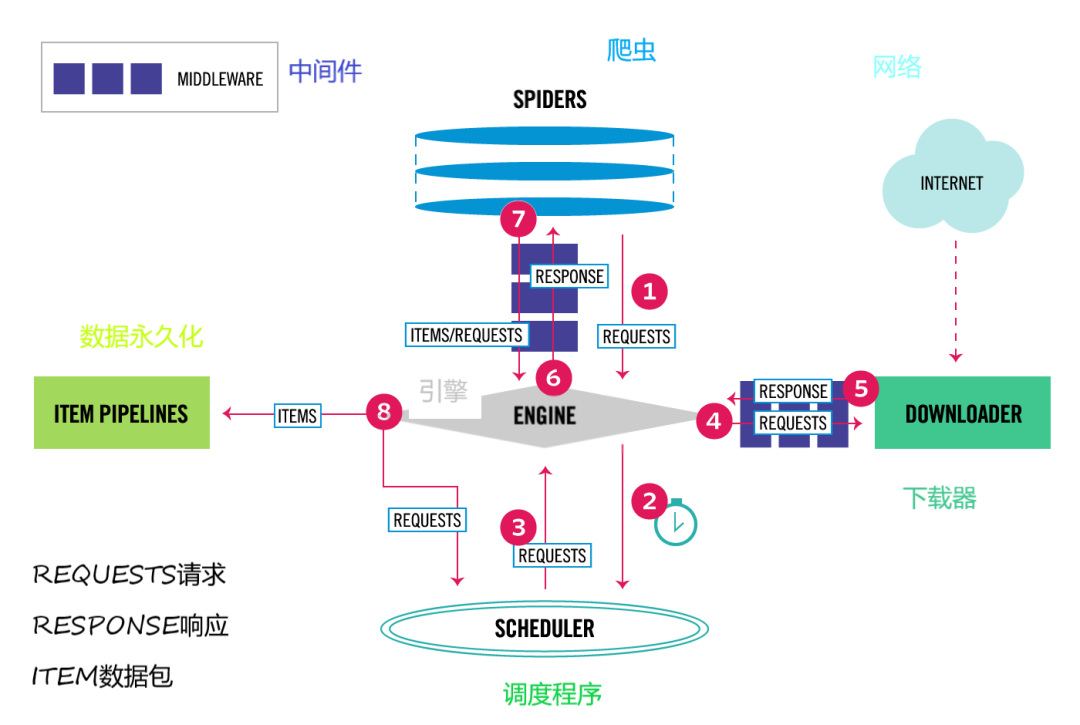
深入理解Scrapy
Scrapy是什么 An open source and collaborative framework for extracting the data you need from websites. In a fast, simple, yet extensible way. Scrapy是适用于Python的一个快速、简单、功能强大的web爬虫框架,通常用于抓取web站点并从页面中提取结构化的数…...
想做WMS仓库管理系统,找了好久才找到云表
公司内部仓库管理原方式均基于人工电子表格管理方式来实现收发存管理,没有流程化管理,无法保证数据的准确性和及时性,同时现场操作和数据核对会出现不同步的情况,无法提高仓库的运作效率,因此,我们基于云表…...
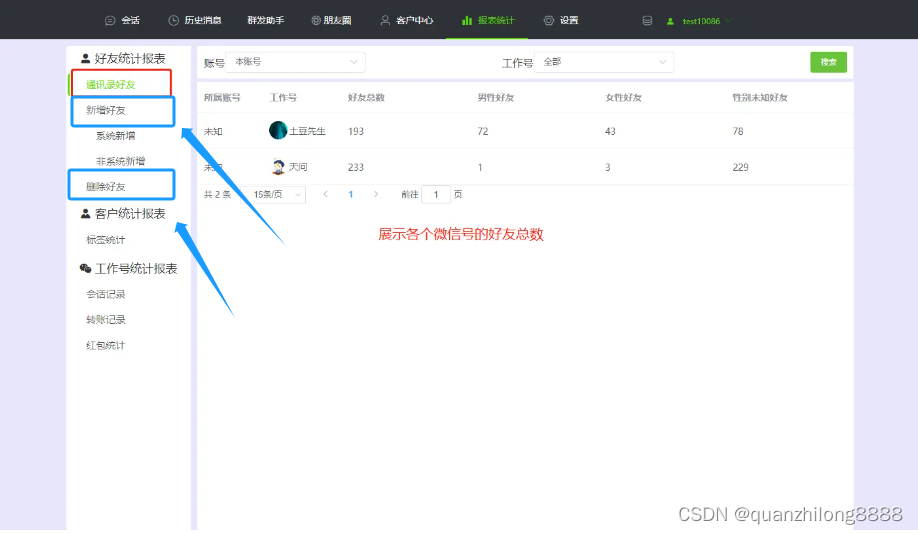
公司销售个人号如何管理?
微信管理系统可以帮助企业解决哪些问题呢? 一、解决聊天记录监管问题 1.聊天记录的保存,让公司的管理者可以随时查看公司任意销售与客户的聊天记录,不用一个一个员工逐一去看,方便管理; 2.敏感词监控,管理者…...

COLE HERSEE 48408 工业4.0、制造业X和元宇宙
COLE HERSEE 48408 工业4.0、制造业X和元宇宙 需要数据来释放工业4.0的全部潜力——价值链中的所有公司都可以访问大量数据。一个新的互联数据生态系统旨在提供解决方案:制造业x。 在德国联邦经济事务和气候行动部以及BDI、VDMA和ZVEI贸易协会的密切合作下,实施制…...
【Vue基础-数字大屏】加载动漫效果
一、需求描述 当网页正在加载而处于空白页面状态时,可以在该页面上显示加载动画提示。 二、步骤代码 1、全局下载npm install -g json-server npm install -g json-server 2、在src目录下新建文件夹mock,新建文件data.json存放模拟数据 {"one&…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
