机器学习:基于主成分分析(PCA)对数据降维
机器学习:基于主成分分析(PCA)对数据降维
作者:AOAIYI
作者简介:Python领域新星作者、多项比赛获奖者:AOAIYI首页
😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏📁评论📒+关注哦!👍👍👍
📜📜📜如果有小伙伴需要数据集和学习交流,文章下方有交流学习区!一起学习进步!💪
| 专栏案例:机器学习 |
|---|
| 机器学习:基于逻辑回归对某银行客户违约预测分析 |
| 机器学习:学习k-近邻(KNN)模型建立、使用和评价 |
| 机器学习:基于支持向量机(SVM)进行人脸识别预测 |
| 决策树算法分析天气、周末和促销活动对销量的影响 |
| 机器学习:线性回归分析女性身高与体重之间的关系 |
文章目录
- 机器学习:基于主成分分析(PCA)对数据降维
- 一、实验目的
- 二、实验原理
- 三、实验环境
- 四、实验内容
- 五、实验步骤
- 1.数据准备
- 2.PCA分析
- 3.查看主成分的解释能力
- 4.主成分轴(Principal Axes)的可视化
- 5.基于PCA的降维
- 6.降维处理
- 7.PCA逆向处理
- 8.使用digits.data训练PCA模型并将结果可视化
- 总结
一、实验目的
1、了解数据降维的各种算法原理
2、熟练掌握sklearn.decomposition中降维方法的使用
二、实验原理
主成分分析算法(Principal Component Analysis, PCA)的目的是找到能用较少信息描述数据集的特征组合。它意在发现彼此之间没有相关性、能够描述数据集的特征,确切说这些特征的方差跟整体方差没有多大差距,这样的特征也被称为主成分。这也就意味着,借助这种方法,就能通过更少的特征捕获到数据集的大部分信息。
主成分分析原理
设法将原来变量重新组合成一组新的相互无关的几个综合变量,同时根据实际需要从中可以取出几个较少的总和变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析,也是数学上处理降维的一种方法。主成分分析是设法将原来众多具有一定相关性(比如P个指标),重新组合成一组新的互相无关的综合指标来代替原来的指标。通常数学上的处理就是将原来P个指标作线性组合,作为新的综合指标。最经典的做法就是用F1(选取的第一个线性组合,即第一个综合指标)的方差来表达,即Va(rF1)越大,表示F1包含的信息越多。因此在所有的线性组合中选取的F1应该是方差最大的,故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息,再考虑选取F2即选第二个线性组合,为了有效地反映原来信息,F1已有的信息就不需要再出现在F2中,用数学语言表达就是要求Cov(F1,F2)=0,则称F2为第二主成分,依此类推可以构造出第三、第四,……,第P个主成分。

sklearn中主成分分析的模型
class sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False, svd_solver=’auto’, tol=0.0, iterated_power=’auto’, random_state=None)
sklearn.decomposition.PCA参数介绍
接下来我们主要基于sklearn.decomposition.PCA类来讲解如何使用scikit-learn进行PCA降维。PCA类基本不需要调参,一般来说,我们只需要指定要降维到的维度,或者希望降维后主成分的方差和占原始维度所有特征方差和的比例阈值就可以了。
现在我们介绍一下sklearn.decomposition.PCA的主要参数:
-
- n_components:这个参数指定了希望PCA降维后的特征维度数目。最常用的做法是直接指定降维到的维度数目,此时n_components是一个大于等于1的整数。当然,我们也可以指定主成分的方差和所占的最小比例阈值,让PCA类自己去根据样本特征方差来决定降维到的维度数,此时n_components是一个(0,1]之间的浮点数。当然,我们还可以将参数设置为"mle",此时PCA类会用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维。我们也可以使用默认值,即不输入n_components,此时n_components=min(样本数,特征数)。
-
- whiten:判断是否进行白化。所谓白化,就是对降维后的数据的每个特征进行归一化,让方差都为1。对于PCA降维本身来说,一般不需要白化。如果在PCA降维后有后续的数据处理动作,可以考虑白化。默认值是False,即不进行白化。
-
- svd_solver:即指定奇异值分解SVD的方法,由于特征分解是奇异值分解SVD的一个特例,一般的PCA库都是基于SVD实现的。有4个可以选择的值:{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。'randomized’一般适用于数据量大,数据维度多同时主成分数目比例又较低的PCA降维,它使用了一些加快SVD的随机算法。'full’则是传统意义上的SVD,使用了scipy库中的实现。‘arpack’和’randomized’的适用场景类似,区别是’randomized’使用的是scikit-learn中的SVD实现,而’arpack’直接使用了scipy库的sparse SVD实现。默认是’auto’,即PCA类会自己去权衡前面讲到的三种算法,选择一个合适的SVD算法来降维。一般来说,使用默认值就够了。
除了这些输入参数外,有两个PCA类的成员值得关注。第一个是explained_variance_,它代表降维后的各主成分的方差值。方差值越大,则说明越是重要的主成分。第二个是explained_variance_ratio_,它代表降维后的各主成分的方差值占总方差值的比例,这个比例越大,则越是重要的主成分。
三、实验环境
Python 3.9
Anaconda 4
Jupyter Notebook
四、实验内容
本实验介绍了主成分分析算法PCA并以实例验证
五、实验步骤
1.数据准备
1.导入所需的模块
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns;sns.set()
%matplotlib inline
2.构建示例数据
#创建随机数生成器
rng=np.random.RandomState(1)
X=np.dot(rng.rand(2,2),rng.randn(2,200)).T plt.scatter(X[:,0],X[:,1])
plt.axis("equal")
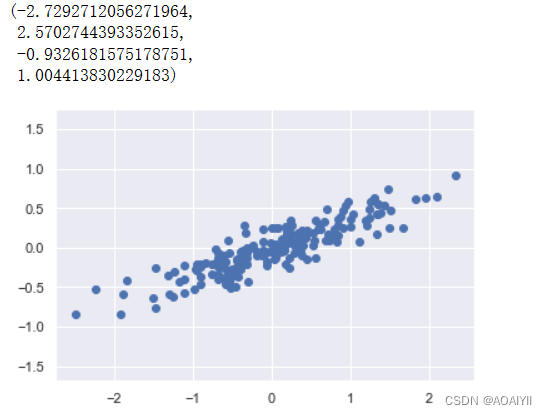
如上所示,第一组示例数据为一组样本量为200的随机的二维数组
2.PCA分析
1.导入 Scikit-Learn 中用于主成分分析的 PCA 模块,构建一个主成分分析模型对象,并进行训练。在这次构建中,我们设定 PCA 函数的参数 n_components 为2,这意味这我们将得到特征值最大的两个特征向量
from sklearn.decomposition import PCA
pca=PCA(n_components=2)
#使用fit()方法拟合模型
pca.fit(X)

n_components参数表示PCA算法中所要保留的主成分个数n,也即保留下来的特征个数n
2.模型训练完成后, components_ 属性可以查看主成分分解的特征向量:
print(pca.components_)

3.使用.shape方法查看矩阵形状
pca.components_.shape

4.使用type()方法查看pca.components_类型
type(pca.components_)
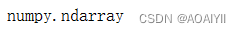
3.查看主成分的解释能力
1.explained_variance_代表降维后的各主成分的方差值。方差值越大,则说明越是重要的主成分
pca.explained_variance_
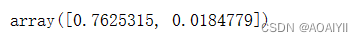
4.主成分轴(Principal Axes)的可视化
1.我们可以通过如下方式将主成分分析中的特征向量描绘出来,下图中向量的起点为样本数据的均值
def draw_vector(v0,v1,ax=None): ax = ax or plt.gca() arrowprops=dict(linewidth=2,shrinkA=0,shrinkB=0) ax.annotate('',v1,v0,arrowprops=arrowprops)
#描绘数据
plt.scatter(X[:,0],X[:,1],alpha=0.2) for length,vector in zip(pca.explained_variance_,pca.components_): v = vector * 3 * np.sqrt(length) draw_vector(pca.mean_,pca.mean_ + v) plt.axis('equal')
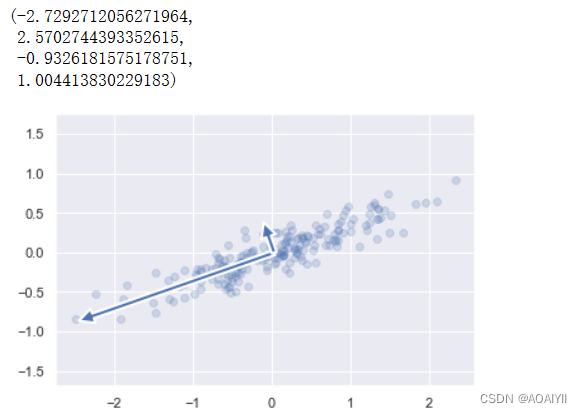
5.基于PCA的降维
1.将n_components设置为1,并使用fit()方法进行拟合
pca=PCA(n_components=1)
pca.fit(X)

6.降维处理
1.将数据X转换成降维后的数据X_pca,并打印X和X_pca的矩阵形状
X_pca=pca.transform(X) print("original shape:",X.shape)
print("transformed shape:",X_pca.shape)
2.使用切片打印X的前十项
X[:10]

3.使用切片打印X_pca的前十项
X_pca[:10]

7.PCA逆向处理
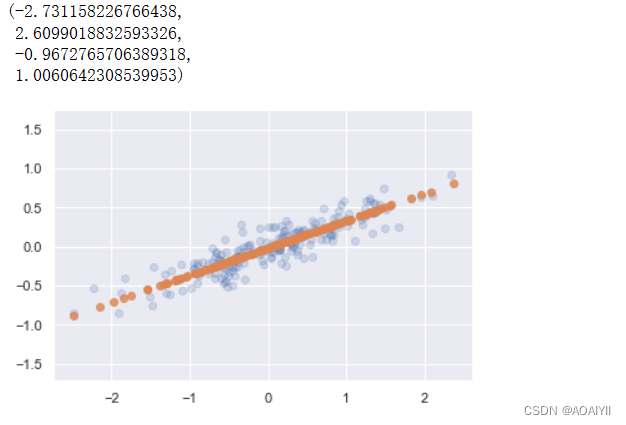
1.将降维后的数据转换成原始数据
X_new=pca.inverse_transform(X_pca)
#描绘数据
plt.scatter(X[:,0],X[:,1],alpha=0.2)
plt.scatter(X_new[:,0],X_new[:,1],alpha=0.8)
plt.axis('equal')
8.使用digits.data训练PCA模型并将结果可视化
1.导入sklearn.datasets模块中的load_digits函数
from sklearn.datasets import load_digits
digits=load_digits()
#查看digits.data的矩阵形状
digits.data.shape

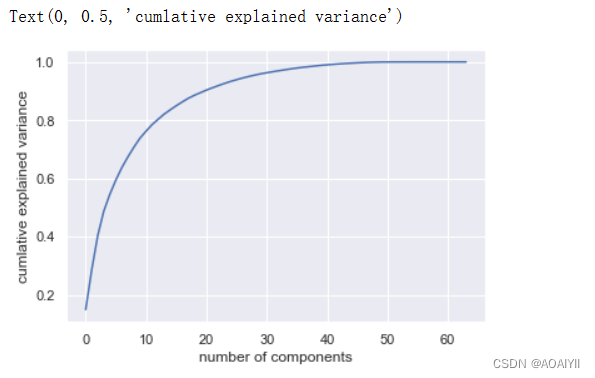
2.使用digits.data训练PCA模型并将结果可视化
pca=PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel("number of components")
plt.ylabel("cumlative explained variance")
总结
主成分分析算法(Principal Component Analysis, PCA)的目的是找到能用较少信息描述数据集的特征组合。它意在发现彼此之间没有相关性、能够描述数据集的特征,确切说这些特征的方差跟整体方差没有多大差距,这样的特征也被称为主成分。这也就意味着,借助这种方法,就能通过更少的特征捕获到数据集的大部分信息。
相关文章:

机器学习:基于主成分分析(PCA)对数据降维
机器学习:基于主成分分析(PCA)对数据降维 作者:AOAIYI 作者简介:Python领域新星作者、多项比赛获奖者:AOAIYI首页 😊😊😊如果觉得文章不错或能帮助到你学习,可…...
软件测试之测试模型
软件测试的发展 1960年代是调试时期(测试即调试) 1960年 - 1978年 论证时期(软件测试是验证软件是正确的)和 1979年 - 1982年 破坏性测试时期(为了发现错误而执行程序的过程) 1983年起,软件测…...
【项目精选】网络考试系统的设计与实现(源码+视频+论文)
点击下载源码 网络考试系统主要用于实现高校在线考试,基本功能包括:自动组卷、试卷发布、试卷批阅、试卷成绩统计等。本系统结构如下: (1)学生端: 登录模块:登录功能; 网络考试模块…...

Python近红外光谱分析与机器学习、深度学习方法融合实践技术
、 第一n入门基础【理论讲解与案 1、Python环境搭建( 下载、安装与版本选择)。 2、如何选择Python编辑器?(IDLE、Notepad、PyCharm、Jupyter…) 3、Python基础(数据类型和变量、字符串和编码、list和tu…...

实例7:树莓派呼吸灯
实例7:树莓派呼吸灯 实验目的 通过背景知识学习,了解digital与analog的区别。通过GPIO对外部LED灯进行呼吸控制,熟悉PWM技术。 实验要求 通过python编程,用GPIO控制LED灯,使之亮度逐渐增大,随后减小&am…...
java 接口 详解
目录 一、概述 1.介绍 : 2.定义 : 二、特点 1.接口成员变量的特点 : 2.接口成员方法的特点 : 3.接口构造方法的特点 : 4.接口创建对象的特点 : 5.接口继承关系的特点 : 三、应用 : 1.情景 : 2.多态 : ①多态的传递性 : ②关于接口的多态参数和多态…...
用 Visual Studio 升级 .NET 项目
现在,你已可以使用 Visual Studio 将所有 .NET 应用程序升级到最新版本的 .NET!这一功能可以从 Visual Studio 扩展包中获取,它会升级你的 .NET Framework 或 .NET Core 网页和桌面应用程序。一些项目类型仍正在开发中并将在不久的未来推出&a…...

JavaWeb中FilterListener的神奇作用
文章目录1,Filter1.1 Filter概述1.2 Filter快速入门1.2.1 开发步骤1.3 Filter执行流程1.4 Filter拦截路径配置1.5 过滤器链1.5.1 概述1.5.2 代码演示1.5.3 问题2,Listener2.1 概述2.2 分类2.3 代码演示最后说一句1,Filter 1.1 Filter概述 F…...

移动端布局
参考链接:抖音-移动端适配 一、移动端布局 flexiblepostcss-pxtorem vue-h5-template 老版本:动态去计算scale,并不影响rem的计算,好处是解决了1px的问题,但是第三方库一般都用dpr为1去做的,这就导致地图或…...

前端无感登录,大文件上传
后端设置token的一个失效时间,前端在token失效后不用重新登录 1,在相应中拦截,判断token返回过期后,调用刷新token的方法 2,后端返回过期的时间,前端判断过期的时间,然后到期后调用对应的方法…...
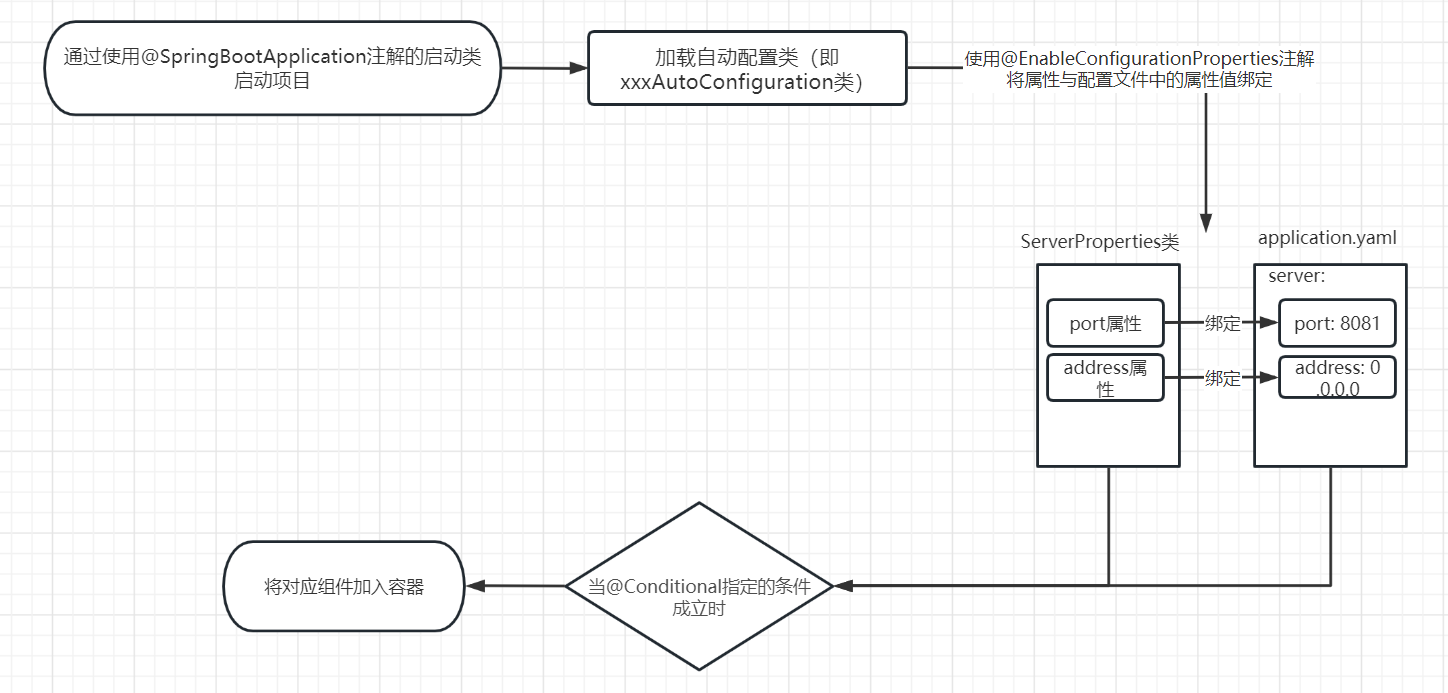
Spring Boot系列03--自动配置原理
目录1. 相关注解2. 自动配置原理分析3. 自动配置图示Spring Boot的核心优势:自动装配、约定大于配置。 1. 相关注解 ConfigurationProperties(prefix "前缀名")该注解用于自动配置的绑定,可以将application.properties配置中的值注入到 Bean…...
Java多线程(四)---并发编程容器
1.经常使用什么并发容器,为什么?答:Vector、ConcurrentHashMap、HasTable一般软件开发中容器用的最多的就是HashMap、ArrayList,LinkedList ,等等但是在多线程开发中就不能乱用容器,如果使用了未加锁&#…...
Apache Hadoop生态部署-Flume采集节点安装
目录 Apache Hadoop生态-目录汇总-持续更新 一:安装包准备 二:安装与常用配置 2.1:下载解压安装包 2.2:解决guava版本问题 2.3:修改配置 三:修复Taildir问题 3.1:Taildir Source能断点续…...

【OpenFOAM】-算例解析合集
【OpenFOAM】-算例解析合集OlaFlowinterFoamOlaFlow 【OpenFOAM】-olaFlow-算例1- baseWaveFlume 【OpenFOAM】-olaFlow-算例2- breakwater 【OpenFOAM】-olaFlow-算例3- currentWaveFlume 【OpenFOAM】-olaFlow-算例4- irreg45degTank 【OpenFOAM】-olaFlow-算例5- oppositeS…...
数据库和SQL概述)
数据库|(一)数据库和SQL概述
(一)数据库和SQL概述1.1 数据库的好处1.2 数据库的概念1.3 数据库结构特点1.1 数据库的好处 实现数据持久化使用完整的管理系统统一管理,便于查询 1.2 数据库的概念 DB 数据库(database),存储数据的仓库&…...

【java基础】自定义类
文章目录基本介绍自定义类字段方法构造器main方法基本介绍 什么是类这里就不过多赘述了,这里来介绍关于类的几个名词 类是构造对象的模板或蓝图由类构造对象的过程称为创建类的实例封装就是将数据和行为组合在一个包中,并对对象的使用者隐藏具体的实现…...
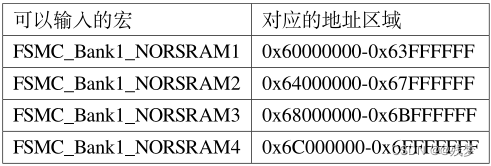
7、STM32 FSMC驱动SRAM
本次使用CubeMx配置FSMC驱动SRAM,XM8A51216 IS62WV51216 原理图: 注意:FSMC_A0必须对应外部设备A0引脚 一、FSMC和FMC区别 FSMC:灵活的静态存储控制器 FMC:灵活存储控制器 区别:FSMC只能驱动静态存储控制器(如&…...
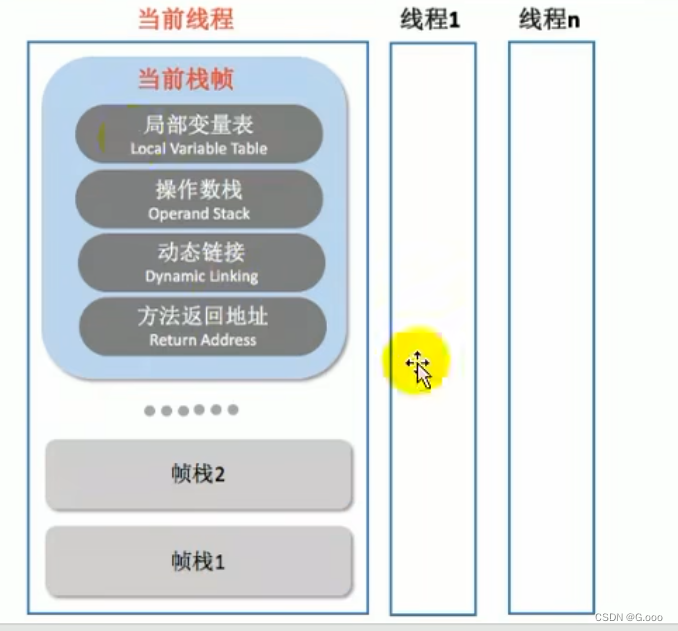
七、虚拟机栈
虚拟机栈出现的背景 1.由于跨平台性的设计,Java的指令都是根据栈来设计的,不同平台CPU架构不同,所以不能设计为基于寄存器的。 2.优点是跨平台,指令集小,编译器容易实现,缺点是性能下降,实现同…...

Linux其他常用命令
Linux其他常用命令查找文件find 命令功能非常强大,通常用在特定目录下搜索符合条件的文件如果省略路径,表示在当前文件夹下查找之前学习的通配符,在使用 find 命令时同时可用演练目标1.搜索桌面目录下,文件名包含1的文件find Desk…...

一次性打包学透 Spring
不知从何时开始,Spring 这个词开始频繁地出现在 Java 服务端开发者的日常工作中,很多 Java 开发者从工作的第一天开始就在使用 Spring Framework,甚至有人调侃“不会 Spring 都不好意思自称是个 Java 开发者”。 之所以出现这种局面…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
