力扣第39题 组合总和 c++ 回溯剪枝题
题目
39. 组合总和
中等
相关标签
数组 回溯
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates =[2,3,6,7],target =7输出:[[2,2,3],[7]] 解释: 2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选, 7 = 7 。 仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
提示:
1 <= candidates.length <= 302 <= candidates[i] <= 40candidates的所有元素 互不相同1 <= target <= 40
思路和解题方法
- 首先定义了两个向量
result和path,用于存储最终的结果集合以及临时的组合方案。其中,result用来存储所有符合条件的组合方案,path则用来存储当前正在尝试的组合方案。- 接着是核心的回溯函数
backtracking。其参数包括候选数字集合candidates,目标值target,当前的数字和sum以及正在搜索的起始位置startIndex。在函数中,我们首先进行递归终止条件的判断:如果当前的数字和已经大于目标值,则说明当前的组合不可能满足条件,直接返回;如果当前的数字和等于目标值,则说明找到了一组符合条件的组合,将其加入结果集合中,并返回。- 接着,我们从给定的起始位置
startIndex开始枚举候选数字,尝试将它们加入当前的组合中。由于每个数字可以重复使用,所以我们并不是从下一个数字开始递归搜索,而是从当前数字继续搜索。在加入数字后,我们进行一次递归搜索,接着弹出最近加入的数字,尝试下一个数字,直到搜索完所有的数字。- 最后,在主函数中,我们清空了结果向量
result和临时变量path,然后调用backtracking函数从第一个数字开始搜索,直到找到所有可能的组合方案。
复杂度
时间复杂度:
O(2^n)
时间复杂度:
- 回溯算法的时间复杂度通常是指数级别的,它取决于候选数字集合的大小以及目标值的大小。假设候选数字集合的长度为n,目标值为target,则最坏情况下,需要遍历所有可能的组合,时间复杂度为O(2^n)。
空间复杂度
O(m*n + n)
空间复杂度:
- 这段代码的空间复杂度主要是由结果向量
result和临时变量path所占用的空间来决定。结果向量result存储了所有符合条件的组合方案,所以它的空间复杂度为O(m * n),其中m是结果集合的大小,n是每个组合的平均长度。临时变量path在递归过程中被使用,它的空间复杂度为O(n),其中n是候选数字集合的长度。因此,总体的空间复杂度为O(m * n + n)。
c++ 代码
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {// 如果当前的和已经大于目标值,就没有可行的方案了,直接返回if (sum > target) {return;}// 如果当前的和等于目标值,说明找到了一组可行的方案,将其加入结果向量中,并返回if (sum == target) {result.push_back(path);return;}// 从给定的起始位置开始枚举候选数字,尝试加入组合中for (int i = startIndex; i < candidates.size(); i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i); // 继续递归搜索下一个数字sum -= candidates[i]; // 回溯,弹出最近加入的数字path.pop_back();}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {result.clear();path.clear();backtracking(candidates, target, 0, 0); // 初始和为0,从第一个数字开始搜索return result;}
};
c++优化的代码 剪枝
在每次递归调用backtracking函数之前,会判断当前和sum加上候选数字candidates[i]是否大于目标值target。如果大于目标值,就可以终止遍历,因为再往后添加数字只会使得和更大,不可能等于目标值了。这样可以减少无效的搜索操作,提高算法的效率。
具体来说,这个优化部分体现在以下代码片段中:

通过这个优化,可以避免对那些不可能达到目标值的路径进行搜索,从而减少了不必要的操作,提高了算法的效率。
需要注意的是,在应用剪枝优化策略的场景中,候选数字必须是有序的。因此,在调用backtracking函数之前,代码使用了sort(candidates.begin(), candidates.end())对候选数字进行排序,为了保证剪枝的正确性。
class Solution {
private:vector<vector<int>> result; // 存储最终结果vector<int> path; // 存储临时组合方案// 回溯函数void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {if (sum == target) { // 当前和等于目标值,找到一组符合条件的组合result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// 如果当前和加上当前数字已经大于目标值,则终止遍历sum += candidates[i]; // 加入当前数字path.push_back(candidates[i]); // 将当前数字加入临时组合方案backtracking(candidates, target, sum, i); // 继续向后搜索,从当前数字开始sum -= candidates[i]; // 回溯,撤销当前数字path.pop_back(); // 回溯,撤销当前数字的选择}}public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {result.clear(); // 清空结果path.clear(); // 清空临时组合方案sort(candidates.begin(), candidates.end()); // 需要对候选数字进行排序,为了剪枝准备backtracking(candidates, target, 0, 0); // 从第一个数字开始回溯搜索return result; // 返回结果集合}
};
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:

力扣第39题 组合总和 c++ 回溯剪枝题
题目 39. 组合总和 中等 相关标签 数组 回溯 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。 cand…...

qt软件正常运行的崩溃了定位行号方法
软件(debug版exe或者release版exe)在正常运行状态下(不是gdb调试运行),如果软件崩掉,那么会直接闪退,软件什么也做不了,此时无法保存软件中的状态信息,此外,也…...

软件工程与计算总结(十五)详细设计中面向对象方法下的信息隐藏
软件工程与计算总结(十三)详细设计中的模块化与信息隐藏 之前的博客中,模块需要隐藏的决策主要由“职责的实现”and“实现的变更”两类,在面向对象方法中,需要做到的就是: 封装类的职责,隐藏职…...
鸿蒙初体验
下载与安装DevEco Studio 在HarmonyOS应用开发学习之前,需要进行一些准备工作,首先需要完成开发工具DevEco Studio的下载与安装以及环境配置。 进入DevEco Studio下载官网,单击“立即下载”进入下载页面。 DevEco Studio提供了Windows版本和…...

hive复合类型的数据查询
hive数据表创建-CSDN博客 --第一个名字以M开头的 访问数组array 数组( array) 引用方式 列名 [ 元素索引 _ 以 0 开始 ] select * from emp where emp_name[0] rlike "^M"; -- 出生日期是在 5 几年 访问 Map map 引用方式 列名 ["Key"] selec…...
Notes/Domino 14 Early Access Drop3发布
大家好,才是真的好。 其实上周,就是国庆假期的时候,HCL Notes/Domino 14 Early Access Drop3(以下简称EA3)就已经发布,而且和传说中的一样,带来了数项惊人的新特性。 我们先讲讲这一版本新特性…...

前端、后端开发者常用到的免费API整理
以下是我整理的前端、后端工程师在开发中经常使用到的API接口,希望能帮到大家~ 手机号码归属地:可根据手机号码查询其省市区、运营商区号行政区划代码等信息。 上亿条数据囊括最新的170、166、147等号段,更新及时、准确度高。空号检测&#…...

【LeetCode高频SQL50题-基础版】打卡第9天:第46~50题
文章目录 【LeetCode高频SQL50题-基础版】打卡第9天:第46~50题⛅前言患某种疾病的患者🔒题目🔑题解 第二高的薪水🔒题目🔑题解 按日期分组销售产品🔒题目🔑题解 列出指定时间段内所有的下单产品…...
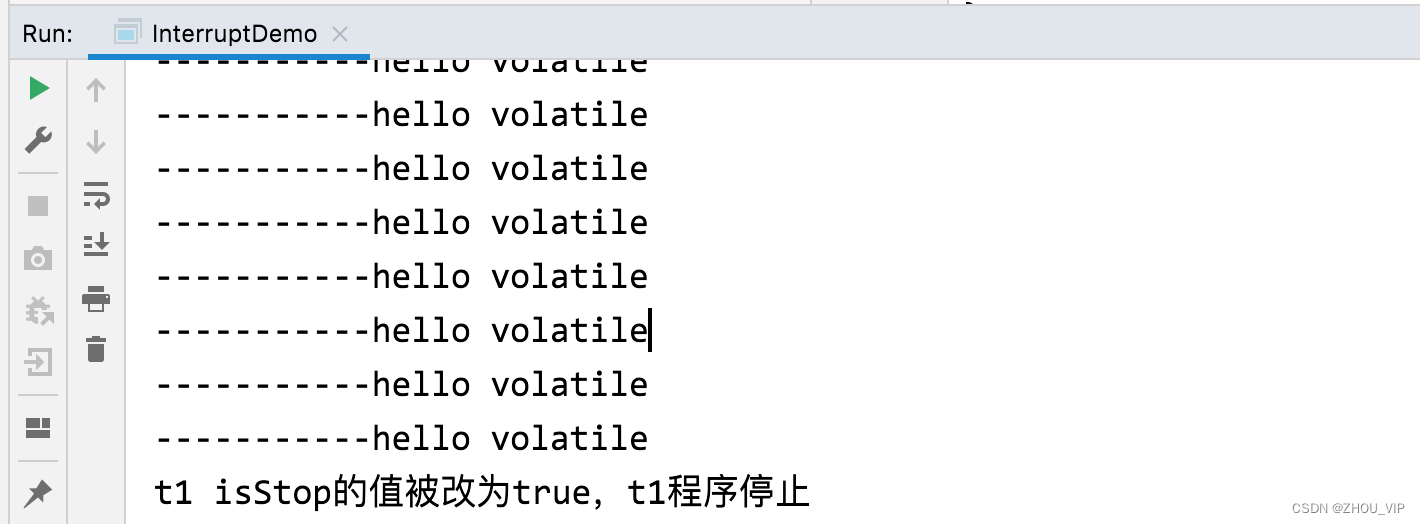
中断机制-通过volatile实现线程中断停止
4.1.4 大厂面试题中断机制考点 如何停止中断运行中的线程? 通过一个volatile变量实现 package com.nanjing.gulimall.zhouyimo.test;import java.util.concurrent.TimeUnit;/*** author zhou* version 1.0* date 2023/10/15 2:34 下午*/ public class InterruptD…...
Elasticsearch 8.11 中的合并更少,摄取更快
作者:ADRIEN GRAND Elasticsearch 8.11 改进了管理索引缓存的方式,从而减少了段合并。 我们对 Elasticsearch 8.11 从索引缓存回收内存的方式进行了重大更改,这有助于减少合并开销,从而加快索引速度。 使用我们的日志跟踪&#x…...

算法村开篇
大家好我是苏麟从今天开始我将带来算法的一些习题和心得体会等等...... 算法村介绍 我们一步步地学习算法本专栏会以闯关的方式来学习算法 循序渐进地系统的学习算法并掌握大部分面试知识 , 期待和大家一起进步 . 索大祝大家学有所成 , 前程似锦....
Leetcode—136.只出现一次的数字【简单】
2023每日刷题(二) Leetcode—136.只出现一次的数字 位运算法 实现代码 int singleNumber(int* nums, int numsSize){int i 0;int res 0;for(; i < numsSize; i) {res ^ nums[i];}return res; }运行结果 之后我会持续更新,如果喜欢我的…...
关于RNNoise、webrtc_ns、三角带通滤波器、对数能量
语音特征参数MFCC提取过程详解 其中讲解了:三角带通滤波器 、计算每个滤波器组输出的对数能量、对数能量、经离散余弦变换(DCT)得到MFCC系数 推荐阅读某乎这位大佬的全部文章: 下面是几篇出自这位大佬的很好的文章: …...
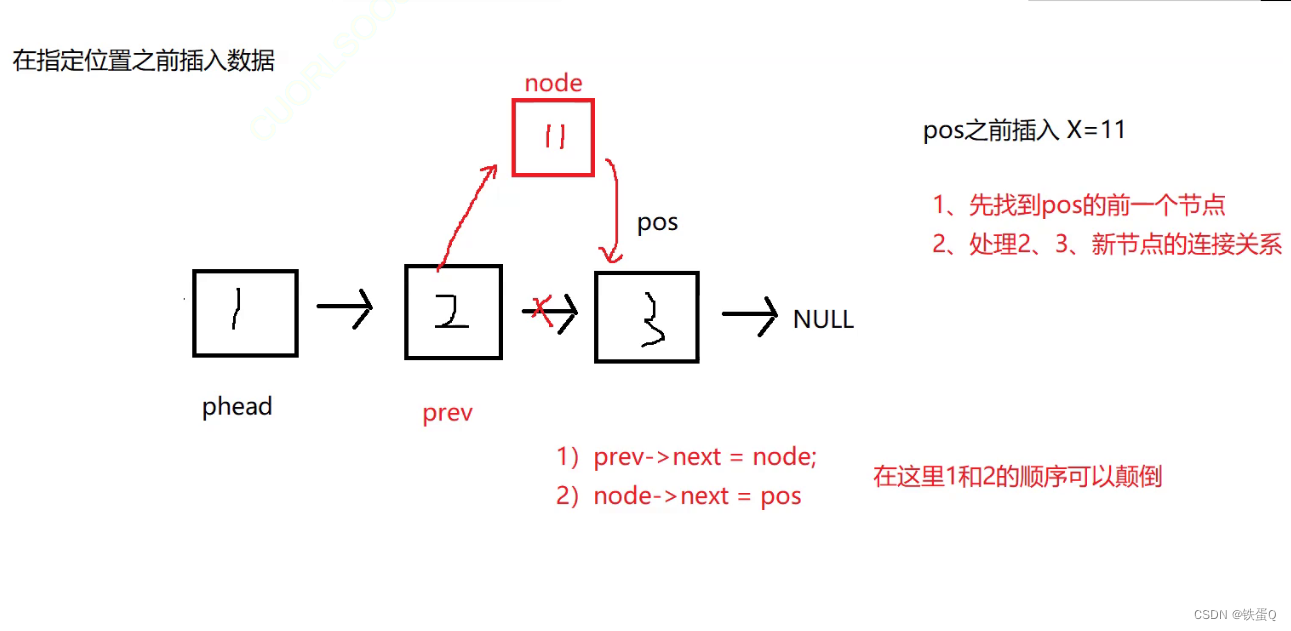
c语言练习89:链表的使用
链表的使用 虽然有这么多的链表的结构,但是我们实际中最常⽤还是两种结构: 单链表 和 双向带头循环链表 1. ⽆头单向⾮循环链表:结构简单,⼀般不会单独⽤来存数据。实际中更多是作为其他数据结 构的⼦结构,如哈希桶、…...
ArkTS及openHarmony
补充 padding:内边距,也就是盒子边和盒子内部的距离 margin:外边距,也就是盒子和盒子的距离 openHarmony应用开发及UI界面 常用布局 Row 水平线性布局核心代码 子控件会共享同一行,也就是都在同一行内 Preview C…...
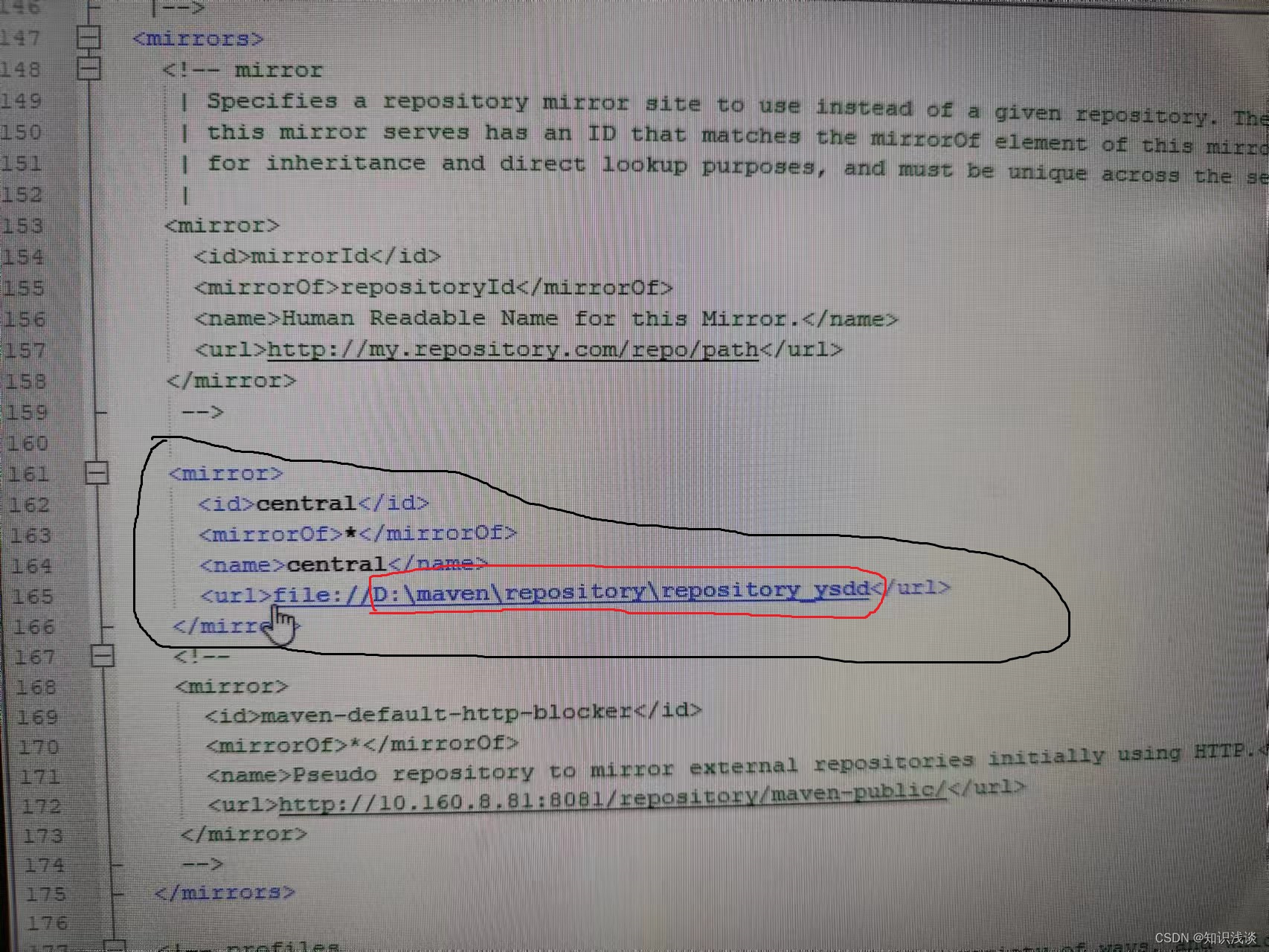
Idea怎么配置Maven才能优先从本地仓库获取依赖
网上的方法 : 在设置中搜索 Runner ,在VM Option中设置参数 -DarchetypeCataloginternal删除 解压后的依赖包中的 _remote.repositories m2e-lastUpdated.properties *.lastUpdated 文件。 上边都没有效果 最终的解决方法,修改maven配置文件settings.xml 主要两个…...

聊聊HttpClient的DnsResolver
序 本文主要研究一下HttpClient的DnsResolver DnsResolver org/apache/http/conn/DnsResolver.java /*** Users may implement this interface to override the normal DNS lookup offered* by the OS.** since 4.2*/ public interface DnsResolver {/*** Returns the IP a…...

剑指智能驾驶,智己LS6胜算几何?
监制 | 何玺 排版 | 叶媛 10月12日,IM智己旗下的新车智己LS6宣布上市。 新车型搭载尖端科技多项,其中以“全画幅数字驾舱屏”、和城市高阶智能辅助驾驶为核心的智驾技术,更是引来众多用户关注。 01 新能源新卷王智己LS6 智己LS6一发布就…...
网络工程师知识点5
71、什么是FTP? FTP是文件传输协议。 FTP传输数据时支持两种传输模式:ASCII模式和二进制模式。 需要TCP的21号端口来建立控制连接 需要TCP的20号端口来建立数据连接 72、什么是telnet? Telnet提供了一个交互式操作界面,允许终端远…...

未来展望:大型语言模型与 SQL 数据库集成的前景与挑战
一、前言 随着 GPT-3、PaLM 和 Anthropic 的 Claude 等大型语言模型 (LLM) 的出现引发了自然语言在人工智能领域的一场革命。这些模型可以理解复杂的语言、推理概念并生成连贯的文本。这使得各种应用程序都能够使用对话界面。然而,绝大多数企业数据都存储在结构化 …...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
