Orin安装ssh、vnc教程
文章目录
- 一:ssh远程
- ==终端的配置==
- ==PC的配置==
- ==MobaXterm的下载==
- 二:VNC Viewer远程图形界面
- ==终端配置==:
- ==PC配置==:
一:ssh远程
终端的配置
1.ifconfig查看终端ip地址
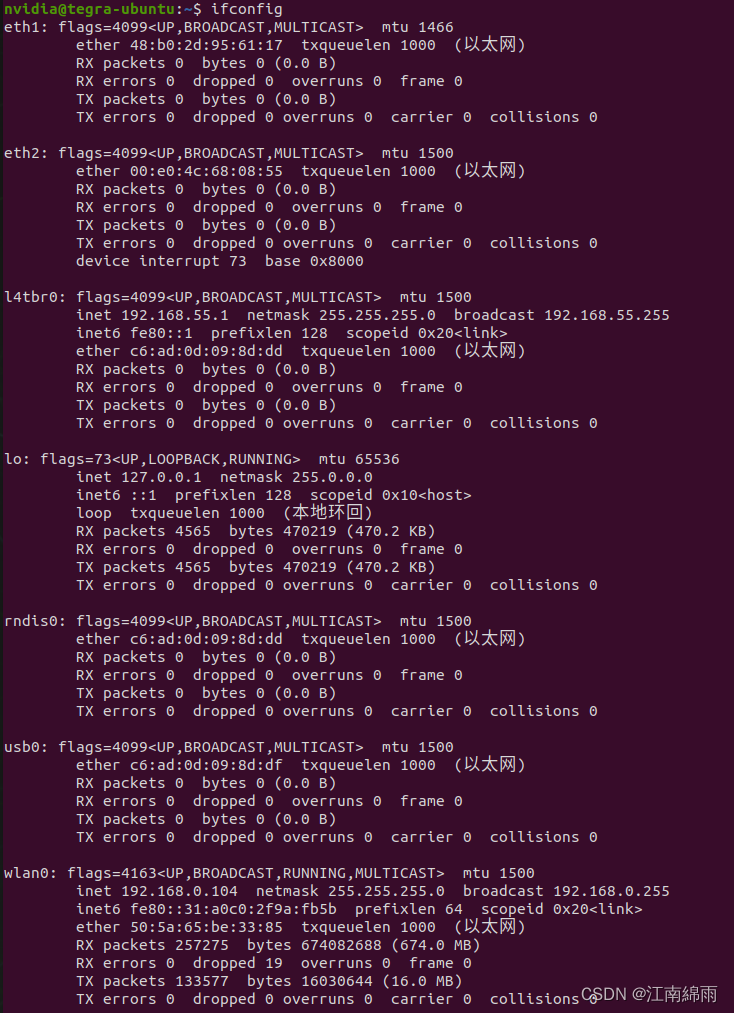
其中的eth是网口,我们需要看的是wlan0下的inet,也就是198.168.0.104,一般而言192.168.0.x指的是路由器分配的地址,基地址是192.168.0.1,我们这里的终端被分配的x是104。
记住用户名,我这里是nvidia。登机密码也要记住,后面连接ssh需要用。
PC的配置
1.安装ssh,然后就可以通过ssh指令直接连接了。windows上的安装教程参考windows下ssh安装与配置,Ubuntu上的安装教程参考ubuntu下ssh安装与配置,里面的密钥可以暂时不设置。
2.运行如下指令,ssh远程连接:
ssh -p 22 nvidia@192.168.0.104 #ssh -p 端口号(默认是22) 主机用户名@ip地址
3.大功告成
MobaXterm的下载
如果想要更华丽的ssh界面,在PC端下载MobaXterm,下载地址官网,选择installer edition,功能更全。这里下载很慢,可以翻墙。
打开MobaXterm界面后,点击session,选择ssh,输入终端ip、端口号、登机密码即可登陆。
二:VNC Viewer远程图形界面
终端配置:
#步骤一、安装vino
sudo apt update
sudo apt install vino#步骤二、(不确定)jetson系列需要更新ubuntu-gnome-desktop服务
sudo apt-get update
sudo apt-get install --only-upgrade ubuntu-gnome-desktop#步骤三、配置 vnc server:
gsettings set org.gnome.Vino prompt-enabled false
gsettings set org.gnome.Vino require-encryption false
注意!!!!Vino一定要是大写的V
最后,还需要使能 设置-共享-屏幕共享,打开后勾选“允许连接控制屏幕”和wifi,并且设置访问密码
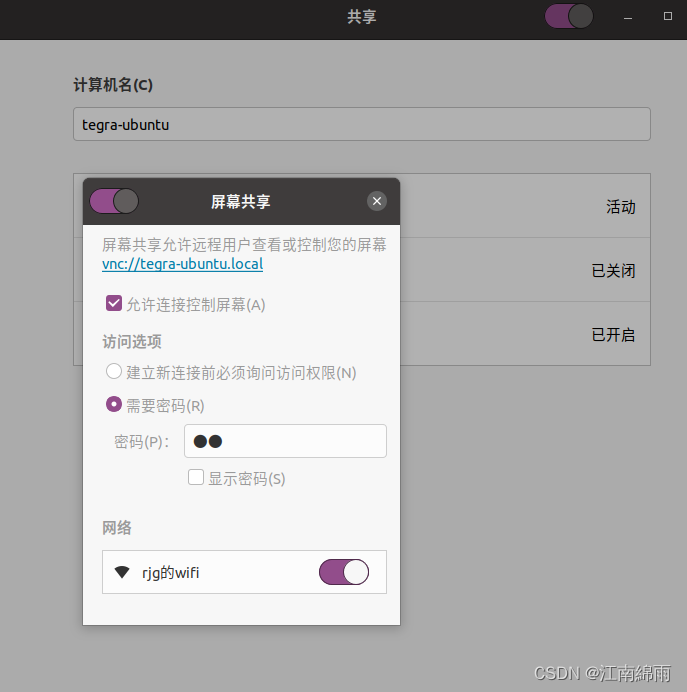
PC配置:
1.打开MobaXterm,session中选择vnc,输入ip地址,注意,port默认就是5900,不要改成22,两者不是一个意思,5900是网址端口,而22是ssh访问端口。

2.回车,输入终端设置的访问密码,成功进入图形界面:

至此,Orin终端上的ssh和vnc教程全部结束,觉得不错的点个赞呦~~~
我是江南咸鱼,愿大家从一而终,不留遗憾!!!
相关文章:

Orin安装ssh、vnc教程
文章目录一:ssh远程终端的配置PC的配置MobaXterm的下载二:VNC Viewer远程图形界面终端配置:PC配置:一:ssh远程 终端的配置 1.ifconfig查看终端ip地址 其中的eth是网口,我们需要看的是wlan0下的inet&#…...
Allegro如何快速删除孤立铜皮操作指导
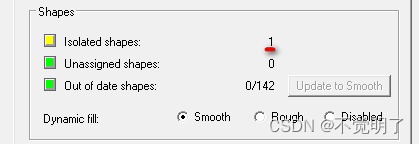
Allegro如何快速删除孤立铜皮操作指导 在做PCB设计的时候,铺铜是常用的设计方式,在PCB设计完成之后,需要删除PCB上孤立的铜皮,即铜皮有网络但是却没有任何连接 如下图 通过Status报表也可以看到Isolated shapes 如何快速地删除孤立铜皮,具体操作如下 点击Shape...

从单管单色到单管RGB,这项MicroLED工艺不可忽视
微显示技术商Porotech,在CES 2023期间展示了最新的MicroLED显示模组。近期,AR/VR光学领域的知名博主Karl Guttag深度分析了该公司的微显示技术,并指出Porotech带来了他见过最有趣的MicroLED技术。Guttag表示:Porotech是本届CES上给…...

6-Java中新建一个文件、目录、路径
文章目录前言1-文件、目录、路径2-在当前路径下创建一个文件3-在当前路径下创建一个文件夹(目录)3.1 测试1-路径已经存在3.2 测试2-路径不存在3.2 创建不存在的路径并新建文件3.3 删除已存在的文件并新建4-总结前言 学习Java中如何新建文件、目录、路径…...

Bootstrap系列之Flex布局
文章目录Bootstrap中的Flexd-flex与d-inline-flex也存在响应式变化flex水平布局flex垂直布局flex水平与垂直也存在响应式变化内容排列(justify-content响应式变化也存在于这里sm,md,lg,xl)子元素对齐方式Align items&a…...
匈牙利算法与KM算法的区别
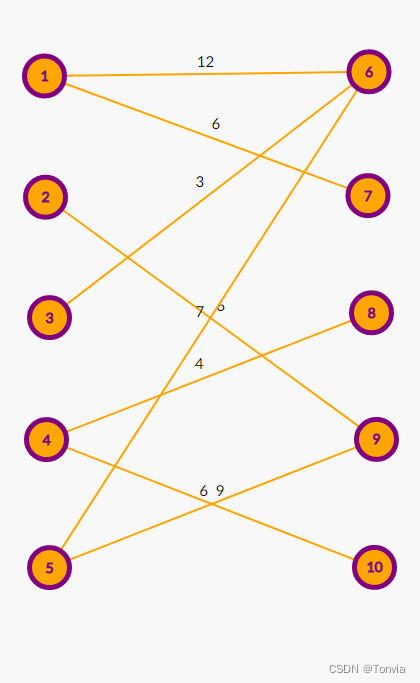
前记 在学习过程中,发现很多博客将匈牙利算法和KM算法混为一谈,当时只管用不管分析区别,所以现在来分析一下两个算法之间的区别。 匈牙利算法在二分图匹配的求解过程中共两个原则: 1.最大匹配数原则 2.先到先得原则 而KM算法求…...

You Only Need 90K Parameters to Adapt Light 论文阅读笔记
这是BMVC2022的论文,提出了一个轻量化的局部全局双支路的低光照图像质量增强网络,有监督。 思路是先用encoder f(⋅)f(\cdot)f(⋅)转到raw-RGB域,再用decoder gt(⋅)g_t(\cdot)gt(⋅)模拟ISP过程转到sRGB域。虽然文章好像没有明确指出&…...
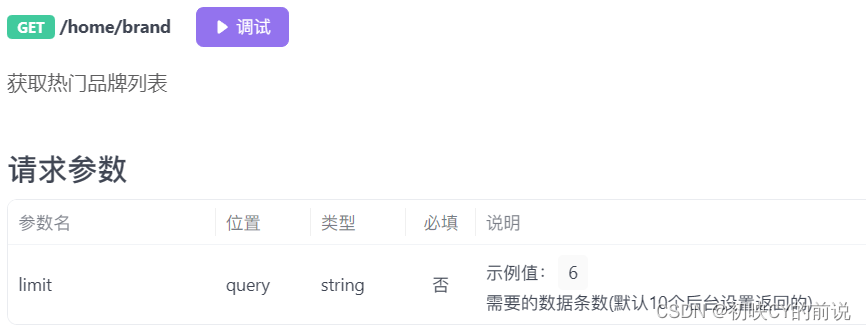
【vue2小知识】实现axios的二次封装
🥳博 主:初映CY的前说(前端领域) 🌞个人信条:想要变成得到,中间还有做到! 🤘本文核心:在vue2中实现axios的二次封装 目录 一、平常axios的请求发送方式 二、axios的一次封装…...

走近php的数组:数组的定义与数组函数
数组是一种数据结构,它由一组元素组成,这些元素可以是相同类型或不同类型。数组是在程序运行时动态创建的,可以根据需要增加或删除元素,因此它们是非常灵活和实用的数据结构。在大多数编程语言中,数组都有一个索引&…...
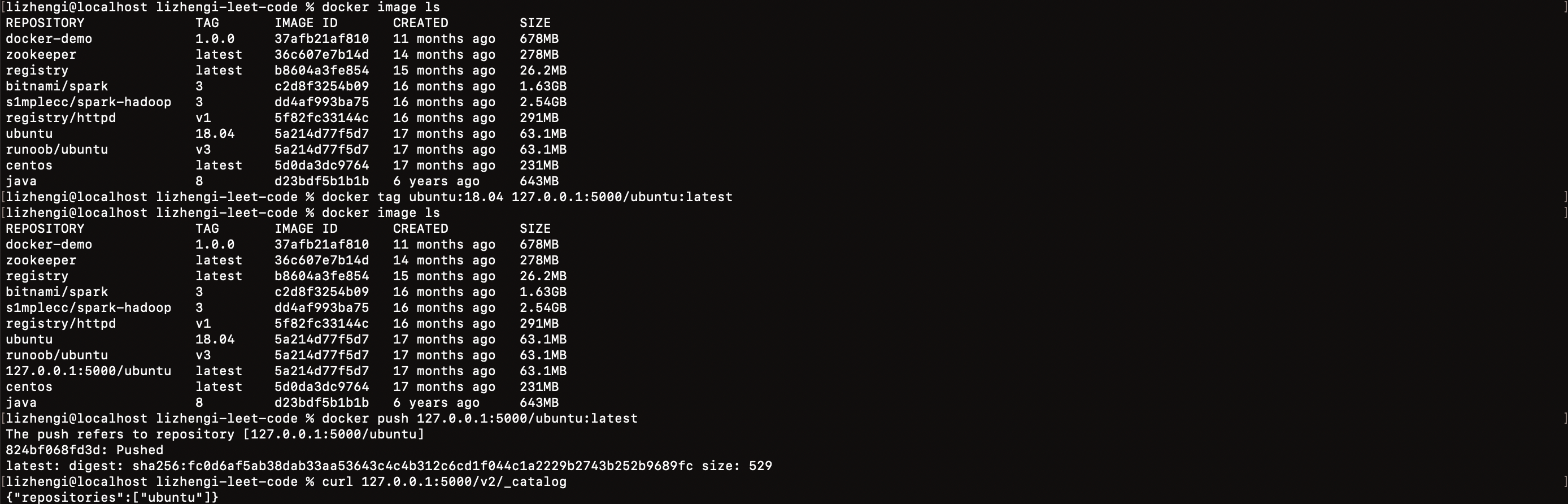
Docker 应用实践-仓库篇
目前 Docker 官方维护了一个公共仓库 Docker Hub,用于查找和与团队共享容器镜像,界上最大的容器镜像存储库,拥有一系列内容源,包括容器社区开发人员、开放源代码项目和独立软件供应商(ISV)在容器中构建和分…...
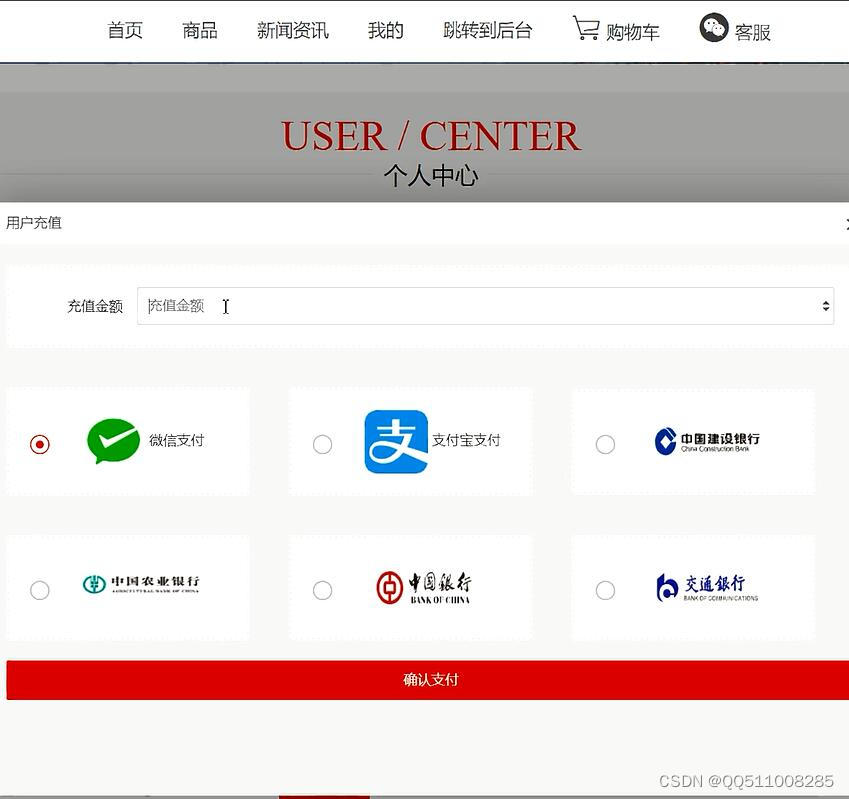
python+django篮球NBA周边商城vue
目 录 第一章 绪 论 1 1.1背景及意义 1 1.2国内外研究概况 1 1.3 研究的内容 1 第二章 关键技术的研究 3 2.1 vue技术介绍 3 myproject/ <-- 高级别的文件夹 |-- myproject/ <-- Django项目文件夹 | |-- myproje…...
抽象类与接口的区别
抽象类什么是抽象类?抽象类是特殊的类,只是不能被实例化;除此以外,具有类的其他特性;重要的是抽象类可以包括抽象方法,这是普通类所不能的。抽象方法只能声明于抽象类中,且不包含任何实现&#…...

1904. 你完成的完整对局数
题目: 一款新的在线电子游戏在近期发布,在该电子游戏中,以 刻钟 为周期规划若干时长为 15 分钟 的游戏对局。这意味着,在 HH:00、HH:15、HH:30 和 HH:45 ,将会开始一个新的对局,其中 HH 用一个从 00 到 23…...

Vue3:自定义指令以及简单的后台管理权限封装
目录 前言: 自定义指令介绍: 局部的自定义指令: 全局自定义指令: 讲讲后台管理权限管理: 前言: 说起这个自定义指令的使用场景,我第一反应就是,后台管理的权限管理,要…...
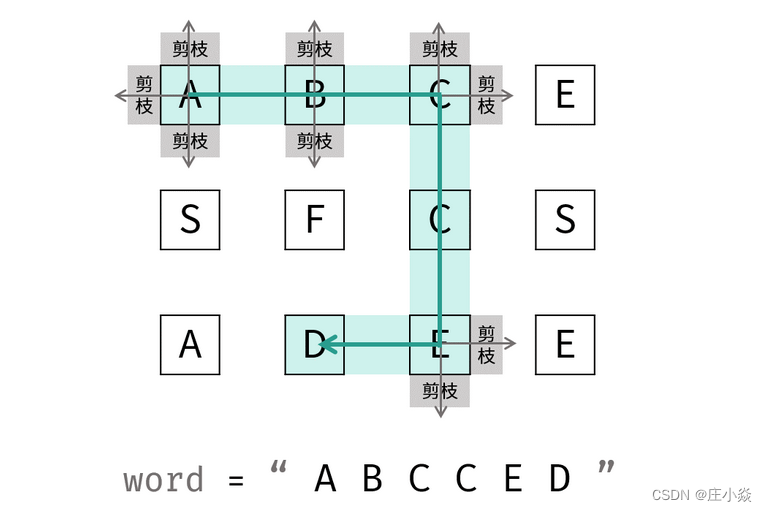
剑指 Offer 12. 矩阵中的路径
摘要 剑指 Offer 12. 矩阵中的路径 一、回溯算法解析 本问题是典型的矩阵搜索问题,可使用 深度优先搜索(DFS) 剪枝解决。 深度优先搜索: 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归,先朝一个方向搜…...
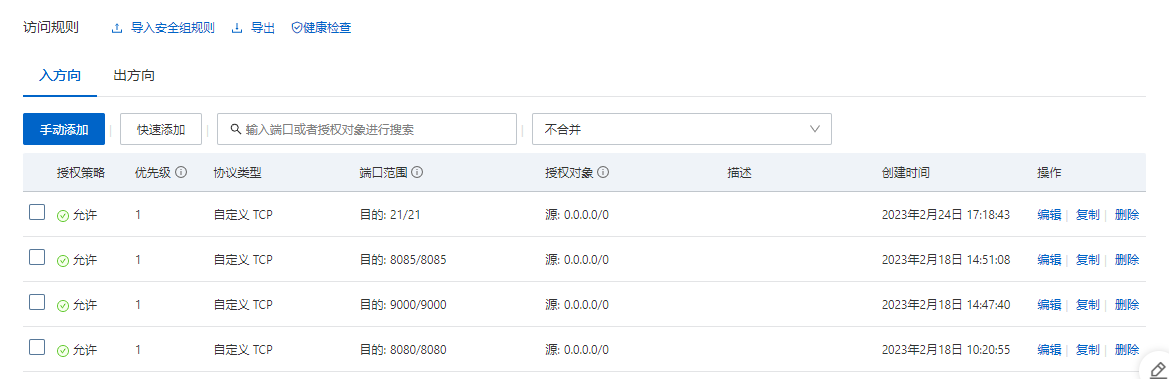
springboot+jersey+tomcat实现跨域方式上传文件到服务器
前言 在服务器上,当我们启动了tomcat,就可以以 http://ip地址:8080/文件路径/文件名 的方式,进行访问到我们服务器上处于tomcat的webapps文件夹下的文件 于是为了可以往上面加文件,我们有两种方式,一种就是直接复制文…...

【微信小程序】-- 常用视图容器类组件介绍 -- view、scroll-view和swiper(六)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &#…...
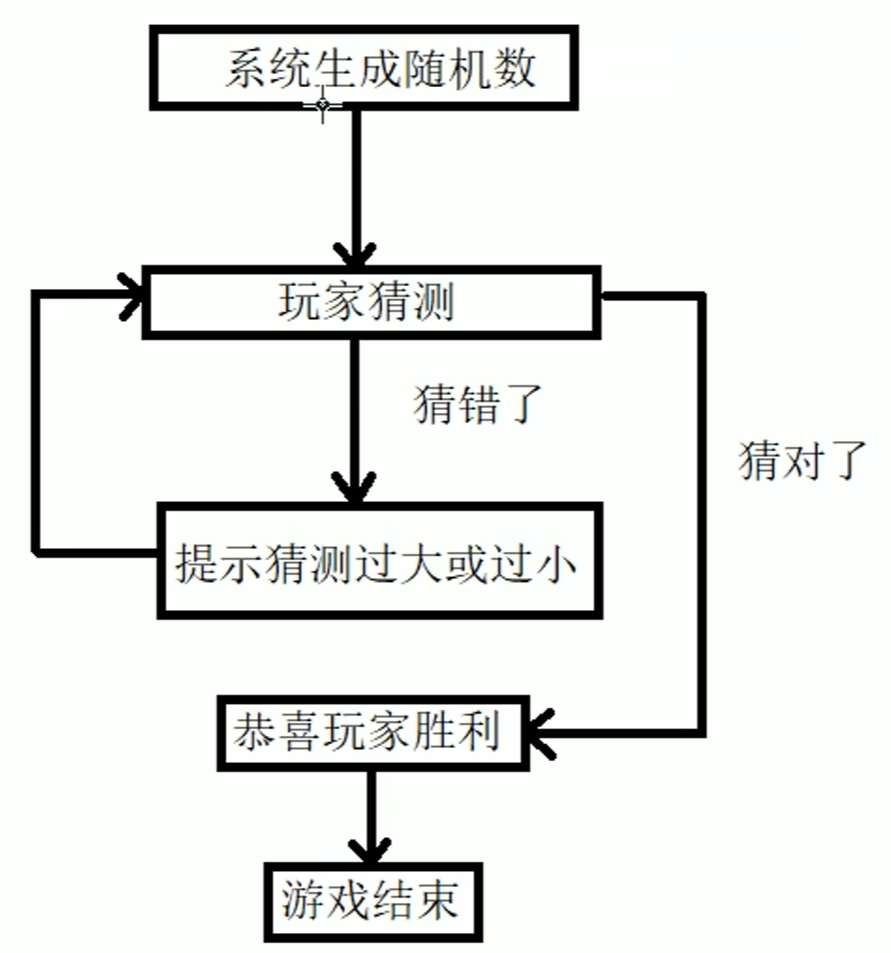
猜数字游戏——C++
我们在有了一定的C基础了以后,简单的实现一个案例(其实只要会while循环结构就行了),我们本章内容会实现猜数字游戏,大家有什么语法疑问可以看看我写的:C快速入门_染柒_GRQ的博客-CSDN博客,该博客…...

整数对最小和
题目描述 给定两个整数数组 array1 array2。数组元素按升序排列,假设从array1 、array2中分别取出一个元素可构成一对元素,现在需要取出K个元素并对取出的所有元素求和,计算和的最小值 注意事项 两对元素如果对应于array1 array2中的两个下…...

2023-2-22 -javaagent
周三,天气晴,7度 Java Agent Java Agent也叫作java探针,可以实现动态修改java字节码,完成额外的功能。在java类编译成字节码,在jvm执行之前,它可以读取修改字节码,以来完成额外的功能。 使用…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
