卡尔曼滤波原理及代码实战
目录
- 简介
- 1.原理介绍
- 场景假设
- (1).下一时刻的状态
- (2).增加系统的内部控制
- (3).考虑运动系统外部的影响
- (4).后验估计:预测结果与观测结果的融合
- 卡尔曼增益K
- 2.卡尔曼滤波计算过程
- (1).预测阶段(先验估计阶段)
- (2).更新阶段(后验估计阶段)
- 3.代码举例
简介
我们可以将卡尔曼滤波看做一种运动模型,它可以在任何含有不确定信息的动态系统中,对系统的下一步走向做出一定的预测,无论是在单目标还是多目标领域都是很常用的一种算法。它最大的优点就是采用递归的方式来解决线性滤波的问题,只需要当前的观测值和前一个周期的预测值就能够进行状态估计。
1.原理介绍
场景假设
假设有一个小车在路上行驶,小车的初始位置和速度用一个状态向量表示:
x^t=[position,velocity]简写为x^t=[pt,vt]\hat x_t=[position,velocity]\\ 简写为\\ \hat x_t=[p_t,v_t] x^t=[position,velocity]简写为x^t=[pt,vt]
因为用两个变量表示了状态向量,所以系统中这两个变量的不确定性和相关性可以用一个协方差矩阵来表示:
Pt=[∑pp∑pv∑vp∑vv]P_t=\begin{bmatrix} \sum_{pp}\quad\sum_{pv}\\ \sum_{vp}\quad\sum_{vv} \end{bmatrix} Pt=[∑pp∑pv∑vp∑vv]
比如前一时刻的速度Vt−1V_{t-1}Vt−1和下一时刻的速度VtV_tVt存在着某种关联,不可能从0突变成光速;
比如前一时刻的速度Pt−1P_{t-1}Pt−1和下一时刻的速度PtP_tPt也存在着某种关联,不可能从我国某地突然变成火星某地。
(1).下一时刻的状态
当小车在做匀速运动时,小车下一时刻的位置和速度如下:
{pt=pt−1+vt−1Δtvt=vt−1\begin{cases} p_t=p_{t-1}+v_{t-1}\Delta t\\ v_t=v_{t-1} \end{cases} {pt=pt−1+vt−1Δtvt=vt−1
矩阵形式为:
[ptvt]=[1Δt01][pt−1vt−1]=Ft[pt−1vt−1]\begin{bmatrix} p_t\\ v_{t} \end{bmatrix}= \begin{bmatrix} 1\quad\Delta t\\ 0\quad1 \end{bmatrix} \begin{bmatrix} p_{t-1}\\ v_{t-1} \end{bmatrix}=F_t\begin{bmatrix} p_{t-1}\\ v_{t-1} \end{bmatrix}[ptvt]=[1Δt01][pt−1vt−1]=Ft[pt−1vt−1]
即:x^t=[1Δt01]x^t−1=Ftx^t−1\hat x_t=\begin{bmatrix} 1\quad\Delta t\\ 0\quad1 \end{bmatrix}\hat x_{t-1}=F_t\hat x_{t-1} x^t=[1Δt01]x^t−1=Ftx^t−1
记状态转移矩阵为,表示小车状态随时间的变化:
Ft=[1Δt01]F_t=\begin{bmatrix}1\quad\Delta t\\0\quad1\end{bmatrix} Ft=[1Δt01]
系统的不确定性和相关性用PtP_tPt表示,而下一时刻的协方差矩阵可表示为(T表示矩阵的转置):
Pt=FtPt−1FtTP_t=F_tP_{t-1}F^T_t Pt=FtPt−1FtT
(2).增加系统的内部控制
如果对小车进行控制,比如加速和减速,假设它的加速度为ata_tat,则小车下一时刻的位置和速度是:
{pt=pt−1+vt−1Δt+12atΔt2vt=vt−1+atΔt\begin{cases} p_t=p_{t-1}+v_{t-1}\Delta t+\frac{1}{2}a_t\Delta t^2\\ v_t=v_{t-1}+a_t\Delta t \end{cases} {pt=pt−1+vt−1Δt+21atΔt2vt=vt−1+atΔt
矩阵形式为:
[ptvt]=[1Δt01][pt−1vt−1]+[Δt22Δt]at=Ft[pt−1vt−1]+Btut\begin{bmatrix} p_t\\ v_{t} \end{bmatrix}= \begin{bmatrix} 1\quad\Delta t\\ 0\quad1 \end{bmatrix} \begin{bmatrix} p_{t-1}\\ v_{t-1}\end{bmatrix}+\begin{bmatrix}\frac{\Delta t^2}{2}\\\Delta t\end{bmatrix}a_t= F_t\begin{bmatrix} p_{t-1}\\ v_{t-1} \end{bmatrix}+B_t u_t [ptvt]=[1Δt01][pt−1vt−1]+[2Δt2Δt]at=Ft[pt−1vt−1]+Btut
记状态控制矩阵为Bt=[Δt22Δt]B_t=\begin{bmatrix} \frac{\Delta t^2}{2}\\ \Delta t \end{bmatrix}Bt=[2Δt2Δt],表明加速度如何改变小车的状态;
记状态控制向量为 utu_tut,表明控制的力度大小和方向。
(3).考虑运动系统外部的影响
小车运动时有很多因素可以对它的位置速度造成影响,比如风俗,路况等,假设外部对小车造成的系统状态误差为wtw_twt,并且它服从高斯分布wtN(0,Qt)w_t~N(0,Q_t)wt N(0,Qt),代入之前的小车运行控制方程,可以得到最终完整的状态预测方程:
x^t=Ftx^t−1+Btut+wtPt=FtPt−1FtT+Qt\hat x_t=F_t\hat x_{t-1}+B_tu_t+w_t\\ P_t=F_tP_{t-1}F^T_t+Q_t x^t=Ftx^t−1+Btut+wtPt=FtPt−1FtT+Qt
除了小车运动的场景,其他物体的状态变化
一般情况下,假设wtw_twt为0即可,将上述公式规范化得到:
x=Fx+BuP=FPFT+Qx=Fx+Bu\\ P=FPF^T+Q x=Fx+BuP=FPFT+Q
(4).后验估计:预测结果与观测结果的融合
在等3步中我们预测出了小车的下一时刻的运动状态,将它的结果称为预测结果,也称为先验估计;不过实际中,汽车上会有里程表、GPS等设备也会提供小车下一时刻的运动状态,称其结果为观测结果。
在实际情况中,预测结果和观测结果都有一定的误差,它们的结果都不一定十分准确,而卡尔曼滤波最重要的作用就是将两者融合,充分利用两者的不确定性得到更加准确的结果,称之为后验估计。
卡尔曼增益K
融合阶段需要用到一个关键的系数卡尔曼增益K,其公式如下(推导过程略):
K=PHT(HPHT)+RK=\frac{PH^T}{(HPH^T)+R} K=(HPHT)+RPHT
P表示变量的不确定性和相关性的协方差矩阵;
R表示传感器观测结果的噪声的协方差矩阵,因为观测值的结果也不一定完美;
H表示预测值和观测值之间的某种关系矩阵,因为它们的结果存在的一定交合;
整体来说,卡尔曼增益表示对观测结果借鉴的程度,相当于一个权重项,让算法知道怎么利用观测与预测进行估计,目的就是让最优估计值的方差更小,是卡尔曼滤波的核心。
2.卡尔曼滤波计算过程
卡尔曼滤波的计算一般分为两步:预测阶段和更新阶段。
(1).预测阶段(先验估计阶段)
x=Fx+BuP=FPFT+Qx=Fx+Bu\\ P=FPF^T+Q x=Fx+BuP=FPFT+Q
(2).更新阶段(后验估计阶段)
K=PHT((HPHT)+R)−1x=x+(K(z−(Hx)))P=(I−(KH))PK=PH^T((HPH^T)+R)^{-1}\\ x=x+(K(z-(Hx)))\\ P=(I-(KH))P K=PHT((HPHT)+R)−1x=x+(K(z−(Hx)))P=(I−(KH))P
x表示系统状态;
z表示传感器的观测结果;
F表示状态转移矩阵;
B表示状态控制矩阵;
u表示状态控制向量;
H表示预测和观测的关系矩阵;
P表示变量的不确定性和相关性的协方差矩阵;
R表示传感器观测结果的噪声的协方差矩阵;
Q表示不确定因素对系统预测结果造成误差的协方差矩阵。
Q和R根据实际情况来定,不断调优根据效果选择一个最优解;
在实际计算中,我们需要关注的是系统的状态x,和它的误差协方差矩阵P,卡尔曼增益K。
3.代码举例
相关文章:

卡尔曼滤波原理及代码实战
目录简介1.原理介绍场景假设(1).下一时刻的状态(2).增加系统的内部控制(3).考虑运动系统外部的影响(4).后验估计:预测结果与观测结果的融合卡尔曼增益K2.卡尔曼滤波计算过程(1).预测阶段(先验估计阶段)(2).更新阶段(后验估计阶段&…...
Jmeter使用教程
目录一,简介二,Jmeter安装1,下载2,安装三,创建测试1,创建线程组2,创建HTTP请求默认值3,创建HTTP请求4,添加HTTP请求头5,添加断言6,添加查看结果树…...

论文笔记|固定效应的解释和使用
DeHaan E. Using and interpreting fixed effects models[J]. Available at SSRN 3699777, 2021. 虽然固定效应在金融经济学研究中无处不在,但许多研究人员对作用的了解有限。这篇论文解释了固定效应如何消除遗漏变量偏差并影响标准误差,并讨论了使用固…...
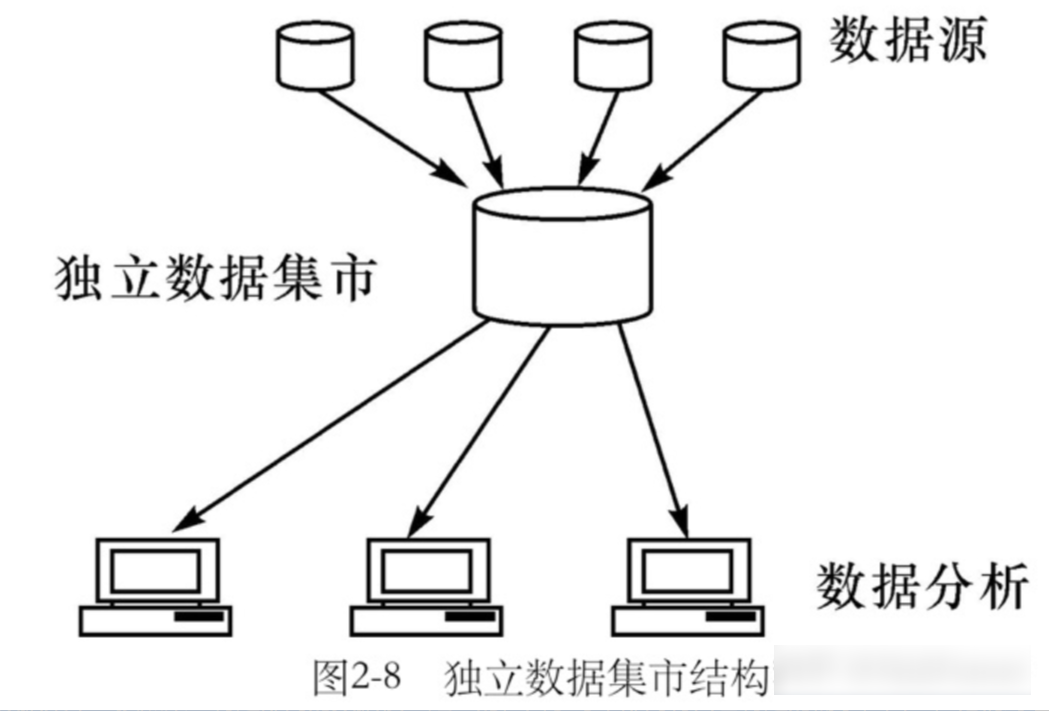
数据集市与数据仓库的区别
数据仓库是企业级的,能为整个企业各个部门的运作提供决策支持;而数据集市则是部门级的,一般只能为某个局部范围内的管理人员服务,因此也称之为部门级数据仓库。 1、两种数据集市结构 数据集市按数据的来源分为以下两种 &#x…...

Golang学习Day3
😋 大家好,我是YAy_17,是一枚爱好网安的小白。 本人水平有限,欢迎各位师傅指点,欢迎关注 😁,一起学习 💗 ,一起进步 ⭐ 。 ⭐ 此后如竟没有炬火,我便是唯一的…...
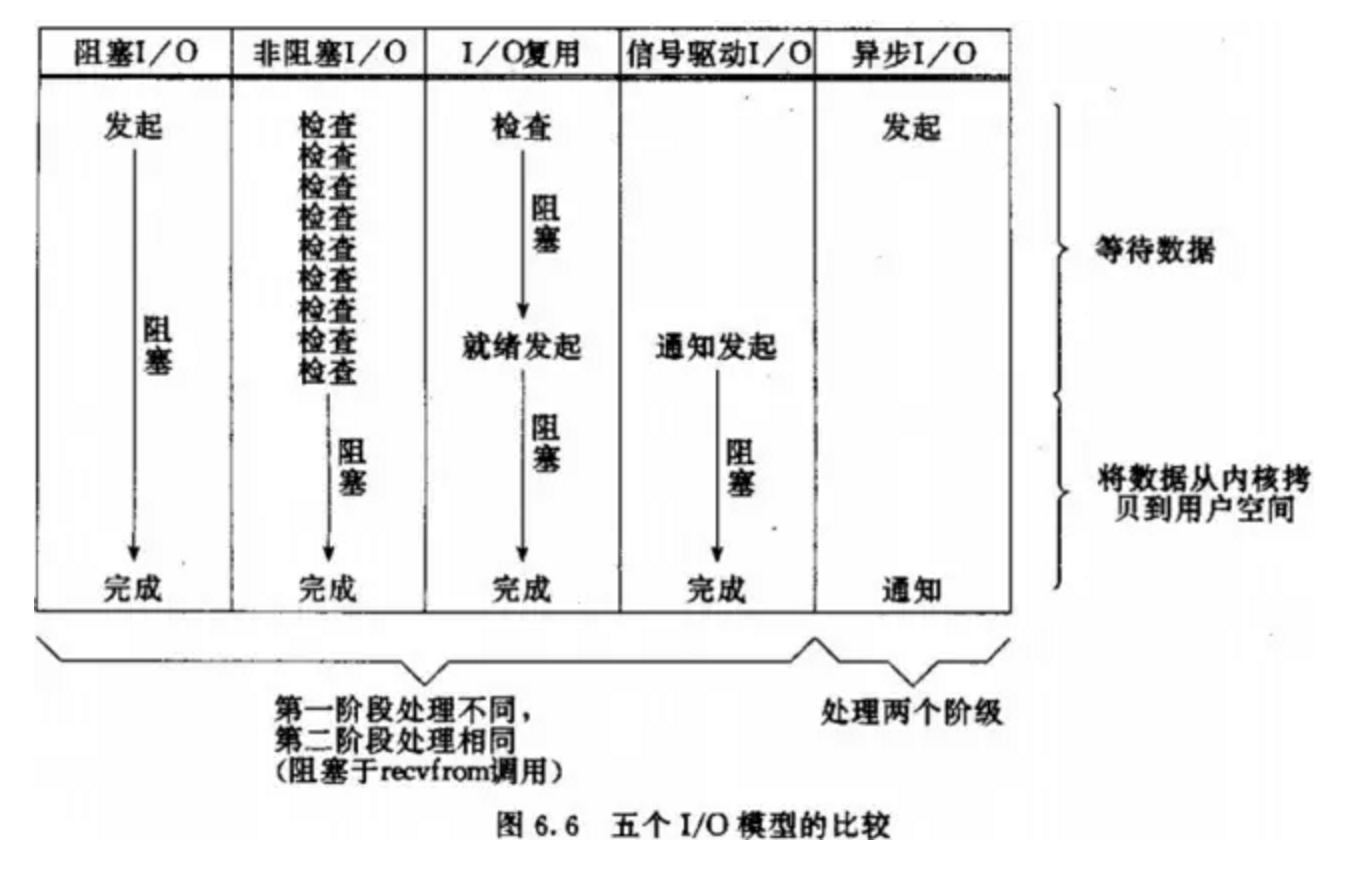
Python并发编程-事件驱动模型
一、事件驱动模型介绍 1、传统的编程模式 例如:线性模式大致流程 开始--->代码块A--->代码块B--->代码块C--->代码块D--->......---&…...
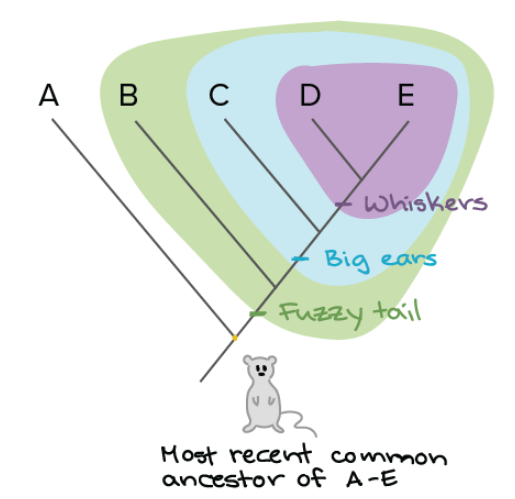
构建系统发育树简述
1. 要点 系统发育树代表了关于一组生物之间的进化关系的假设。可以使用物种或其他群体的形态学(体型)、生化、行为或分子特征来构建系统发育树。在构建树时,我们根据共享的派生特征(不同于该组祖先的特征)将物种组织成…...
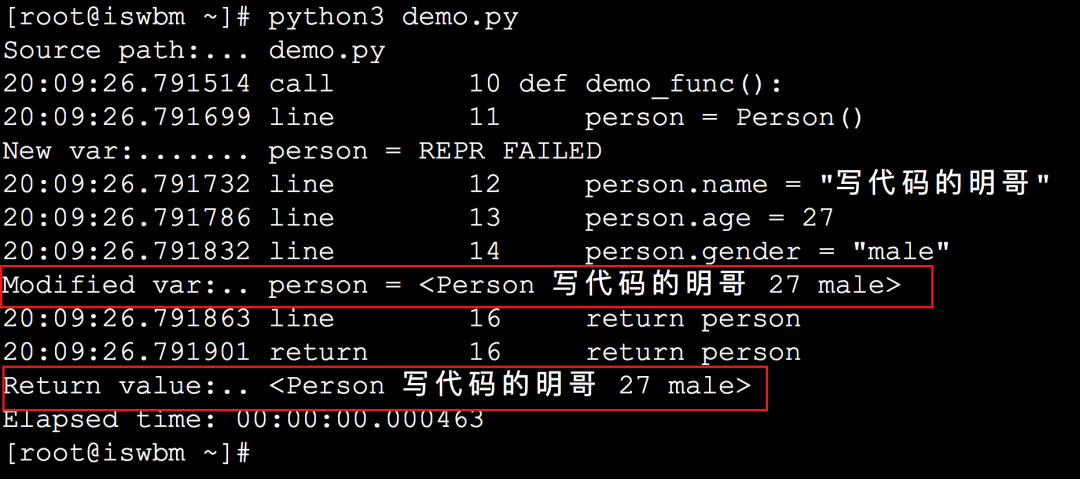
这款 Python 调试神器推荐收藏
大家好,对于每个程序开发者来说,调试几乎是必备技能。 代码写到一半卡住了,不知道这个函数执行完的返回结果是怎样的?调试一下看看 代码运行到一半报错了,什么情况?怎么跟预期的不一样?调试一…...
金三银四吃透这份微服务笔记,面试保准涨10K+
很多人对于微服务技术也都有着一些疑虑,比如: 微服务这技术虽然面试的时候总有人提,但作为一个开发,是不是和我关系不大?那不都是架构师的事吗?微服务不都是大厂在玩吗?我们这个业务体量用得着…...
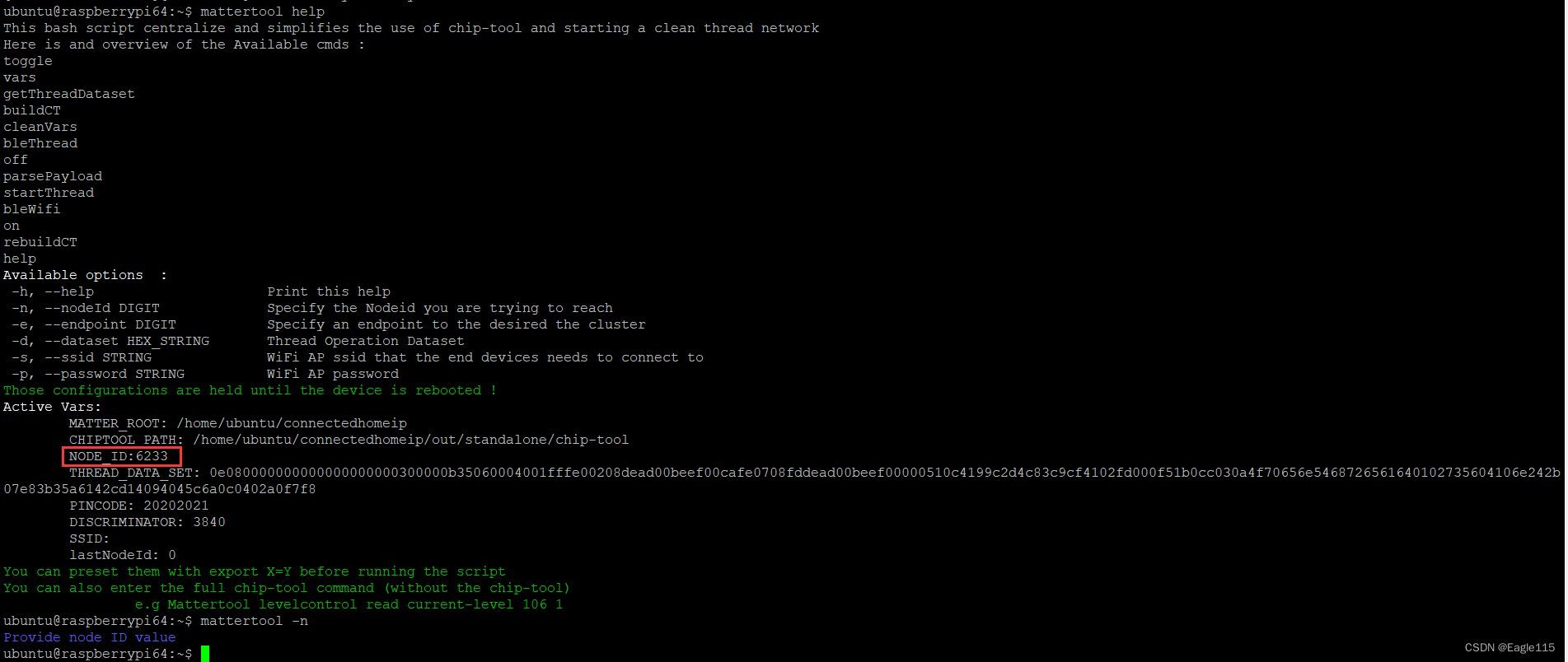
构建matter over Thread的演示系统-efr32
文章目录1. 简介2. 构建测试系统2.1设置 Matter Hub(Raspberry Pi)2.2 烧录Open Thread RCP固件2.3 烧录待测试的matter设备3. 配网和测试:3.1 使用mattertool建立Thread网络3.2 使用mattertool配置设备入网3.3 使用mattertool控制matter设备3.4 查看节点的Node ID等…...

【一天一门编程语言】Matlab 语言程序设计极简教程
Matlab 语言程序设计极简教程 用 markdown 格式输出答案。 不少于3000字。细分到2级目录。 目录 Matlab 语言程序设计极简教程 简介Matlab 工作空间Matlab 基本数据类型Matlab 语句和表达式Matlab 函数和程序Matlab 图形界面程序设计Matlab 应用实例 简介 Matlab是一种编…...
看似平平无奇的00后,居然一跃上岸字节,表示真的卷不过......
又到了一年一度的求职旺季金!三!银!四!在找工作的时候都必须要经历面试这个环节。在这里我想分享一下自己上岸字节的面试经验,过程还挺曲折的,但是还好成功上岸了。大家可以参考一下! 0821测评 …...

BZOJ2142 礼物
题目描述 一年一度的圣诞节快要来到了。每年的圣诞节小E都会收到许多礼物,当然他也会送出许多礼物。不同的人物在小E 心目中的重要性不同,在小E心中分量越重的人,收到的礼物会越多。小E从商店中购买了n件礼物,打算送给m个人 &…...
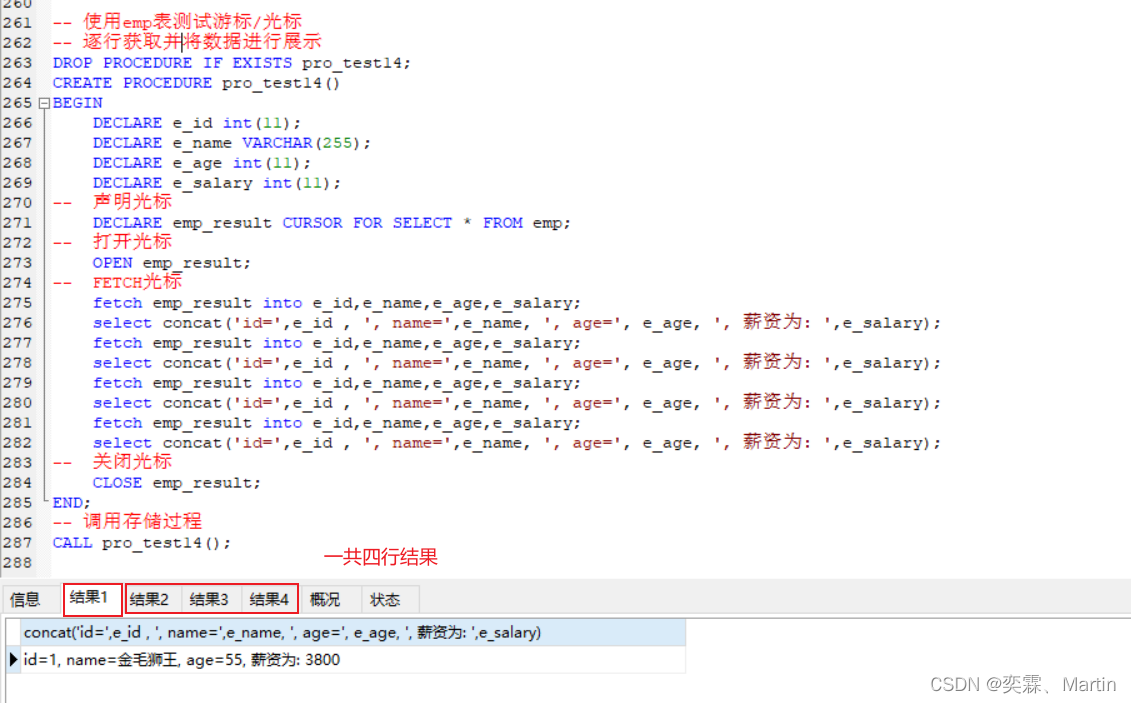
MySQL高级第一讲
目录 一、MySQL高级01 1.1 索引 1.1.1 索引概述 1.1.2 索引特点 1.1.3 索引结构 1.1.4 BTREE结构(B树) 1.1.5 BTREE结构(B树) 1.1.6 索引分类 1.1.7 索引语法 1.1.8 索引设计原则 1.2 视图 1.2.1 视图概述 1.2.2 创建或修改视图 1.3 存储过程和函数 1.3.1 存储过…...

前端面试常用内容——基础积累
1.清除浮动的方式有哪些? 高度塌陷:当所有的子元素浮动的时候,且父元素没有设置高度,这时候父元素就会产生高度塌陷。 清除浮动的方式: 1.1 给父元素单独定义高度 优点: 快速简单,代码少 缺…...
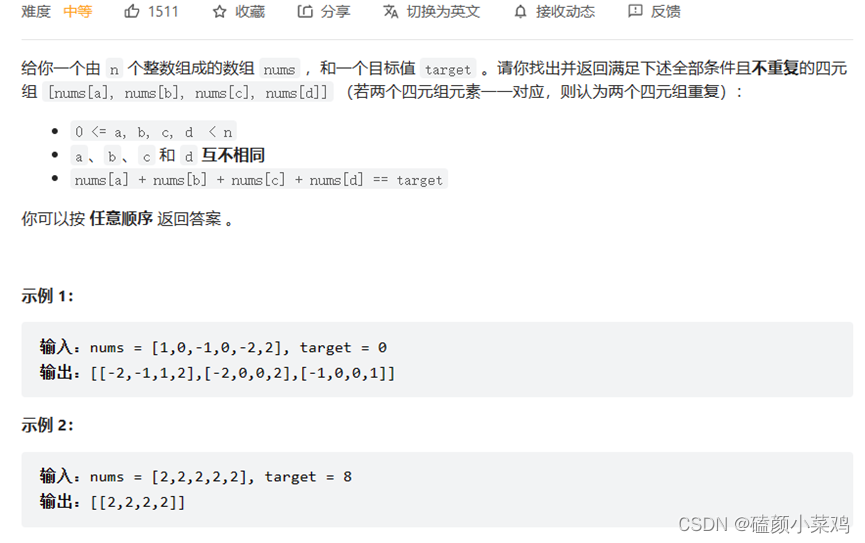
跟着《代码随想录》刷题(三)——哈希表
3.1 哈希表理论基础 哈希表理论基础 3.2 有效的字母异位词 242.有效的字母异位词 C bool isAnagram(char * s, char * t){int array[26] {0};int i 0;while (s[i]) {// 并不需要记住字符的ASCII码,只需要求出一个相对数值就可以了array[s[i] - a];i;}i 0;whi…...
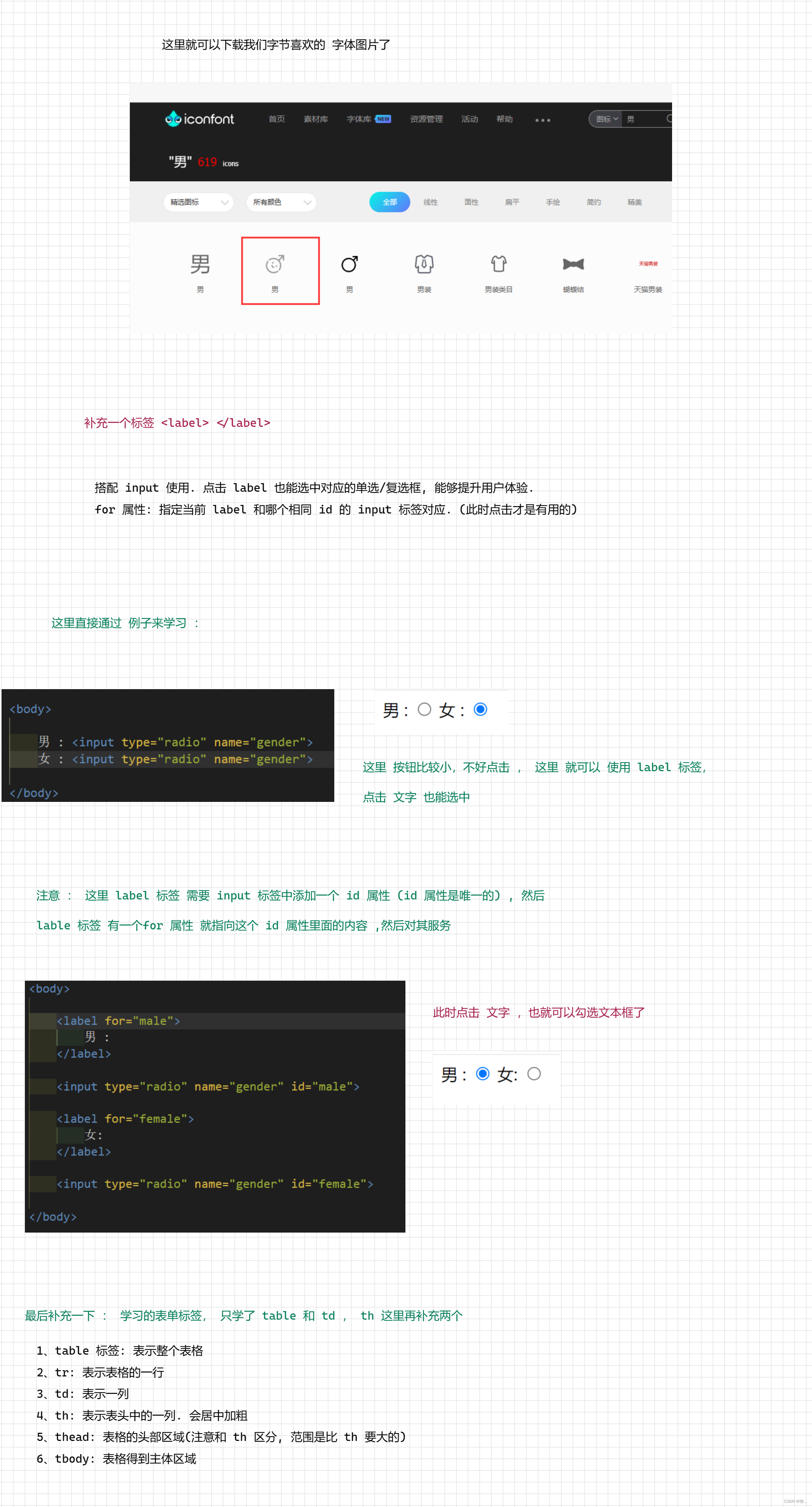
HTML - 扫盲
文章目录1. 前言2. HTML2.1 下载 vscode3 HTML 常见标签3.1 注释标签3.2 标题标签3.3 段落标签3.4 换行标签3.5 格式化标签1. 加粗2. 倾斜3. 下划线3.6 图片标签3.7 超链接标签3.8 表格标签3.9 列表标签4. 表单标签4.1 from 标签4.2 input 标签4.3 select 标签4.4 textarea标签…...
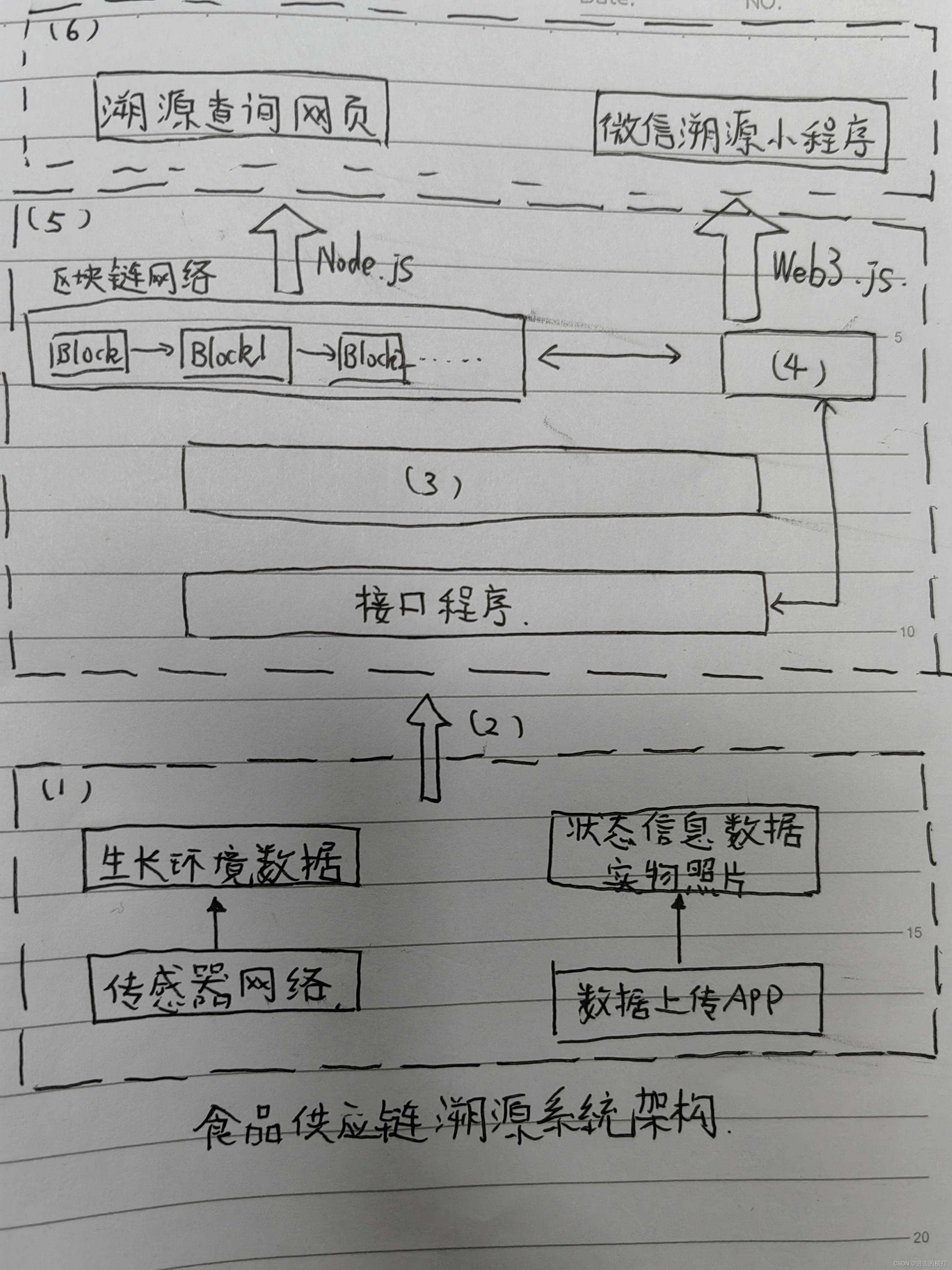
【系统分析师之路】2022上案例分析历年真题
【系统分析师之路】2022上案例分析历年真题 【系统分析师之路】2022上案例分析历年真题【系统分析师之路】2022上案例分析历年真题2022上案例分析历年真题第一题(25分)2022上案例分析历年真题第二题(25分)2022上案例分析历年真题第…...

Python编程规范
Python编程规范 当今Python编程社区有许多关于编程规范的约定和惯例。以下是一些常见的Python编程规范: 1.使用有意义的命名 使用有意义的命名可以使代码更加清晰、易读、易维护。变量、函数、类和模块的命名应该能够明确传达其用途,而不是使用无意义…...
【Java】Spring Boot项目的创建和使用
文章目录SpringBoot的创建和使用1. 什么是Spring Boot?为什么要学Spring Boot?2. Spring Boot项目的优点3. Spring Boot 项目的创建3.1 使用idea创建3.2 接下来创建Spring Boot项目4. 项目目录介绍和运行4.1 运行项目4.2 输出内容5. 总结SpringBoot的创建…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...
