【LeetCode刷题(数据结构与算法)】:数据结构中的常用排序实现数组的升序排列

现在我先将各大排序的动图和思路以及代码呈现给大家
插入排序
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为
止,得到一个新的有序序列
实际中我们玩扑克牌时,就用了插入排序的思想


当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与
array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void InsertSort(int* a, int n)
{// [0,end]有序,把end+1位置的插入到前序序列// 控制[0,end+1]有序for (size_t i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];}else{break;}--end;}a[end + 1] = tmp;}
}
希尔排序
也称缩小增量排序
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个
组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工
作。当到达=1时,所有记录在统一组内排好序
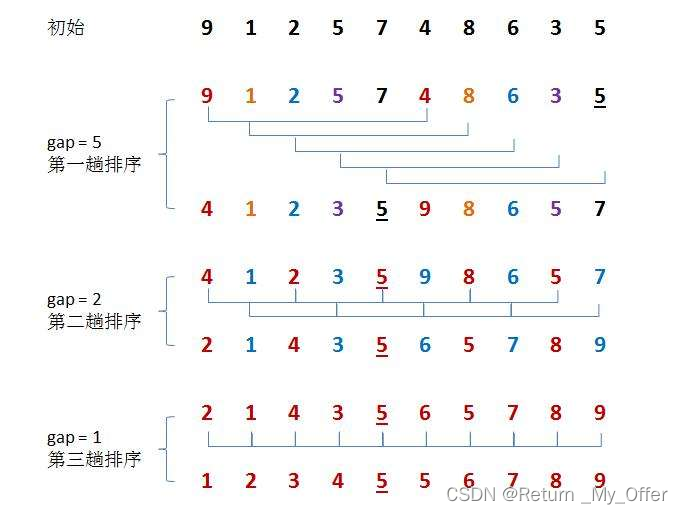
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就
会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。 - 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的
希尔排序的时间复杂度都不固定:
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){//gap = gap / 2;gap = gap / 3 + 1;for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}
选择排序
2.2.1基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的
数据元素排完
2.2.2 直接选择排序:
在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换在剩余的array[i]–array[n-2]集合中,重复上述步骤,直到集合剩余1个元素

直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
void InsertSort(int* a, int n)
{// [0,end]有序,把end+1位置的插入到前序序列// 控制[0,end+1]有序for (size_t i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];}else{break;}--end;}a[end + 1] = tmp;}
}堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种 它是
通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 找出小的那个孩子if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{// 向下调整建堆// O(N)for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}// O(N*logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}

- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
交换排序
基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排
序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动
冒泡排序

冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中
的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右
子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,同学们在写递归框架时可想想二叉
树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可
将区间按照基准值划分为左右两半部分的常见方式有:
- hoare版本

- 挖坑法

- 前后指针版本

快速排序优化 - 三数取中法选key
- 递归到小的子区间时,可以考虑使用插入排序
// 三数取中
int GetMidi(int* a, int left, int right)
{int mid = (left + right) / 2;// left mid rightif (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]) // mid是最大值{return left;}else{return right;}}else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]) // mid是最小{return left;}else{return right;}}
}
// Hoare
int PartSort1(int* a, int left, int right)
{int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;while (left < right){// 找小while (left < right && a[right] >= a[keyi]){--right;}// 找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);return left;
};// 挖坑法
int PartSort2(int* a, int left, int right)
{int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int key = a[left];// 保存key值以后,左边形成第一个坑int hole = left;while (left < right){// 右边先走,找小,填到左边的坑,右边形成新的坑位while (left < right && a[right] >= key){--right;}a[hole] = a[right];hole = right;// 左边再走,找大,填到右边的坑,左边形成新的坑位while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}// 前后指针
int PartSort3(int* a, int left, int right)
{int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int prev = left;int cur = prev + 1;int keyi = left;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[keyi]);return prev;
}
// [begin, end]
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort3(a, begin, end);// [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}
快速排序的特性总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)

归并排序
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and
Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有
序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:


归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
void _MergeSort(int* a, int* tmp, int begin, int end)
{if (end <= begin)return;int mid = (end + begin) / 2;// [begin, mid][mid+1, end]_MergeSort(a, tmp, begin, mid);_MergeSort(a, tmp, mid+1, end);// 归并到tmp数据组,再拷贝回去// a->[begin, mid][mid+1, end]->tmpint begin1 = begin, end1 = mid;int begin2 = mid+1, end2 = end;int index = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}// 拷贝回原数组memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, tmp, 0, n - 1);free(tmp);
}
根据自己的喜好进行数组的升序即可 这里不过多要求
相关文章:

【LeetCode刷题(数据结构与算法)】:数据结构中的常用排序实现数组的升序排列
现在我先将各大排序的动图和思路以及代码呈现给大家 插入排序 直接插入排序是一种简单的插入排序法,其基本思想是: 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个…...

【HTML+CSS】零碎知识点
公告滚动条 <!DOCTYPE html> <html><head><title>动态粘性导航栏</title><style>.container {background: #00aeec;overflow: hidden;padding: 20px 0;}.title {float: left;font-size: 20px;font-weight: normal;margin: 0;margin-left:…...
嵌入式开发学习之STM32F407串口(USART)收发数据(三)
嵌入式开发学习之STM32F407串口(USART)收发数据(三) 开发涉及工具一、选定所使用的串口二、配置串口1.配置串口的I/O2.配置串口参数属性3.配置串口中断4.串口中断在哪里处理5.串口如何发送字符串 三、封装串口配置库文件1.创建头文…...
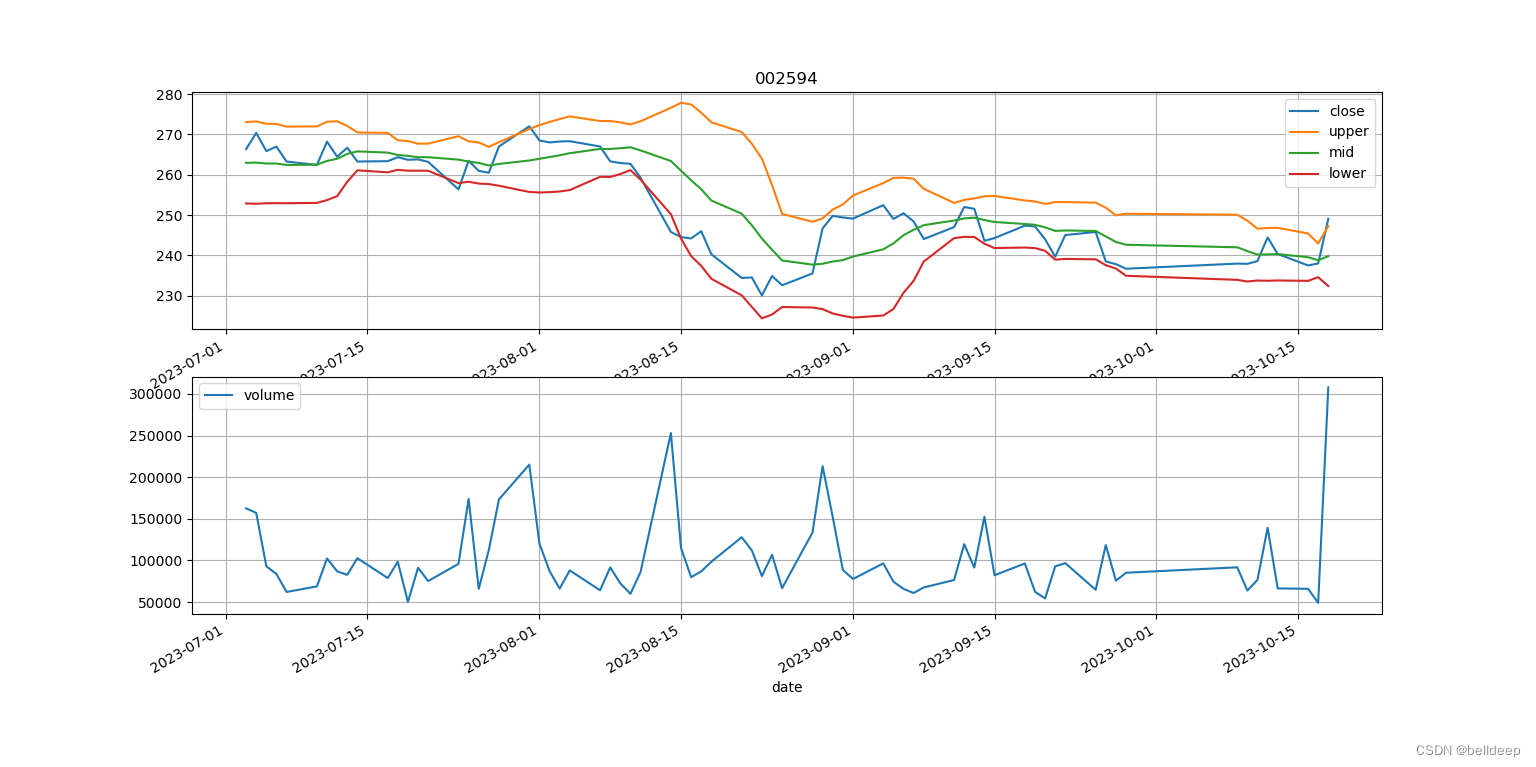
python:talib.BBANDS 画股价-布林线图
python 安装使用 TA_lib 安装主要在 http://www.lfd.uci.edu/~gohlke/pythonlibs/ 这个网站找到 TA_Lib-0.4.24-cp310-cp310-win_amd64.whl pip install /pypi/TA_Lib-0.4.24-cp310-cp310-win_amd64.whl 编写 talib_boll.py 如下 # -*- coding: utf-8 -*- import os impor…...

ESP32网络开发实例-自定义主机名称
自定义主机名称 文章目录 自定义主机名称1、软件准备2、硬件准备3、代码实现ESP32 的默认主机名是 expressif。 但是,如果正在使用多个 ESP32 设备,并且在某些时候希望在软接入点模式下使用它们时通过名称来区分设备。 例如,在基于物联网的项目中有多个节点,例如温度、湿度…...
【ELK 使用指南 3】Zookeeper、Kafka集群与Filebeat+Kafka+ELK架构(附部署实例)
EFLKK 一、Zookeeper1.1 简介1.2 zookeeper的作用1.3 Zookeeper的特点1.5 Zookeeper的数据结构1.6 Zookeeper的应用场景1.7 Zookeeper的选举机制(重要)1.7.1 第一次启动时1.7.2 非第一次启动时 二、Zookeeper集群部署2.1 安装前准备2.2 安装 ZookeeperSt…...

手写redux的connect方法, 使用了subscribe获取最新数据
一. 公共方法文件 1. connect文件 import React, { useState } from "react"; import MyContext from "./MyContext"; import _ from "lodash";// 模拟react-redux的 connect高阶函数 const connect (mapStateToProps, mapDispatchToProps) &…...

数据结构--B树
目录 回顾二叉查找树 如何保证查找效率 B树的定义 提炼 B树的插入和删除 概括B树的插入方法如下 B树的删除 导致删除时,结点不满足关键字的个数范围时(需要借) 如果兄弟不够借,需要合体 回顾B树的删除 B树 B树的查找 …...

【音视频|ALSA】基于alsa-lib开发ALSA应用层程序--附带源码
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...
嵌入式养成计划-43----QT QMainWindow中常用类的使用--ui界面文件--资源文件的添加--信号与槽
一百零九、QMainWindow中常用类的使用 109.1 菜单栏 QMenuBar 菜单栏 QMenuBar 最多只能有一个 109.2 工具栏 QToolBar 工具栏 QToolBar 可以有多个 109.3 状态栏QStatusBar 状态栏 QStatusBar 最多只能有一个 109.4 浮动窗口QDockWidget 浮动窗口 可以有多个 109.5 代…...

【Yarn】清除Yarn的缓存,更新Yarn本身、更新项目的依赖项
要清除Yarn的缓存,可以运行以下命令: yarn cache clean这将清除Yarn的缓存目录。 要更新Yarn本身,可以运行以下命令: yarn self-update这将下载并安装最新版本的Yarn。 如果要更新项目的依赖项,可以运行以下命令&a…...
)
点云从入门到精通技术详解100篇-雨雾环境下多传感器融合SLAM方法(续)
目录 4 基于球面投影的激光视觉融合里程计 4.1 引言 4.2 视觉惯性里程计 4.2.1特征点提取与匹配...

解决GET请求入参@NotNull验证不生效问题
一、问题 get请求NotNull验证不生效 二、解决方案 两个步骤: 在该方法的controller类上加Validated;在参数面前加NotNull; 三、其他注解 //被注释的元素必须为null Null //被注释的元素不能为null NotNull //被注释的元素必须为true Ass…...

《golang设计模式》第三部分·行为型模式-01-责任链模式(Chain of Responsibility)
文章目录 1 概念1.1 角色1.2 类图 2. 代码示例2.1 设计2.2 代码2.3 类图 1 概念 责任链(Chain of Responsibility)是指将客户端请求处理的不同职责对象组成请求处理链。 客户端只需要将请求交付到该链上,而不需要关心链上含有哪些对象。请求…...
环境变量【使用命令行参数引出环境变量】
前提:命令行参数 大家在写C/C程序的时候肯定见过下面这种情况: main函数里面携带的参数,平常写代码过程中很少用到这两个参数,接下来我们就研究一下 我们也不知道 指针数组argv里面到底保存的是什么,也不知道这个a…...

【Java 进阶篇】JavaScript BOM History 详解
当用户浏览网页时,可以使用JavaScript的BOM (Browser Object Model)中的History对象来访问浏览器的历史记录。这个对象允许您在不更改页面的情况下导航到不同的历史记录项,或者查看有关用户访问过的页面的信息。 在本篇博客中,我们将围绕Jav…...
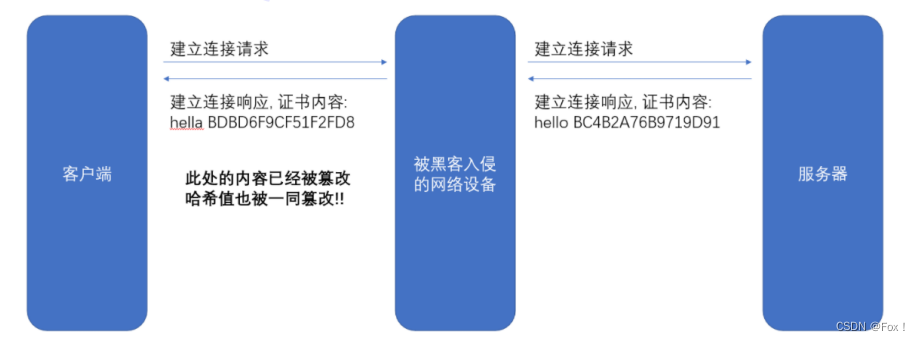
【计算机网络】https协议
文章目录 1 :peach:基本概念:peach:1.1 :apple:什么是HTTPS?:apple:1.2 :apple:什么是加密?:apple:1.3 :apple:常见的加密方式:apple:1.3.1 :lemon:对称加密:lemon:1.3.2 :lemon:⾮对称加密:lemon: 1.4 :lemon:数据指纹:lemon: 2 :peach:HTTPS的⼯作过程…...
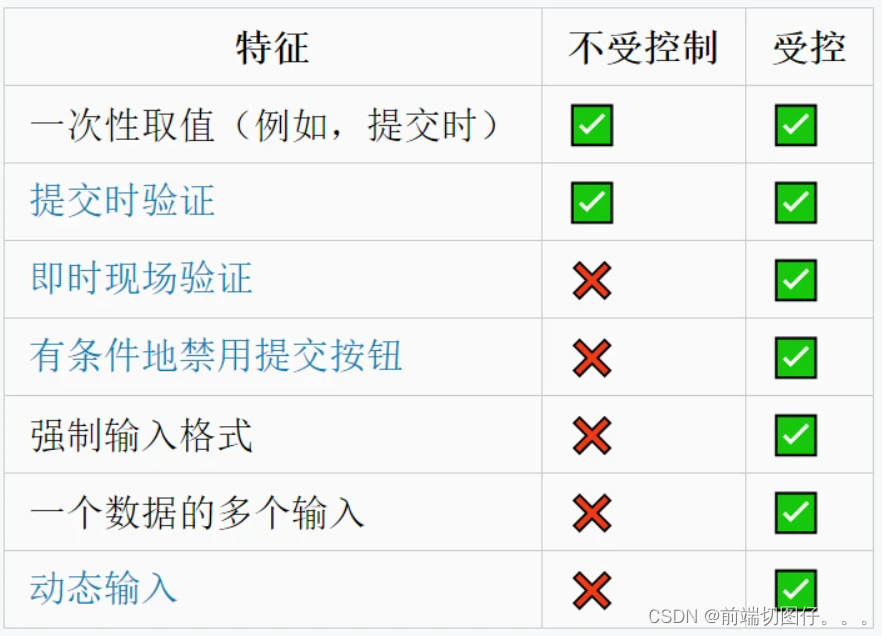
React之受控组件和非受控组件以及高阶组件
一、受控组件 受控组件,简单来讲,就是受我们控制的组件,组件的状态全程响应外部数据 举个简单的例子: class TestComponent extends React.Component {constructor (props) {super(props);this.state { username: lindaidai }…...

中国移动集采120万部,助推国产5G赶超iPhone15
近期媒体纷纷传出消息指中国移动将大规模集采,预计将采购国产5G手机120万台,加上另外两家运营商的集采数量,估计集采数量可能达到300万部,如此将有助于它在国内高端手机市场赶超苹果。 国产5G手机在8月底突然上市,获益…...
华为云HECS服务器下docker可视化(portainer)
一、docker安装 华为云HECS安装docker-CSDN博客 二、portainer安装 portainer地址:Portainer: Docker and Kubernetes Management Platform 当前portainer分CE(开源版) 和 BE(商业版),用CE即可 1 创建…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
