针孔成像模型零基础入门(三)

2020年爆火的Nerf(神经辐射场)横空出世,据说只要用手机拍照,然后喂给模型,就可以生成3D模型了,我试过了,确有此事!
那我们有想过,为什么可以从二维的图片里面获取物体三维的信息吗?
接下来,我们就追根溯源,先从数学和物理的角度来看下三维世界的物体如何通过照相机变成二维的图像信息。
稍微插播:大家支持的话可以关注公众号 AI知识物语(周更三维重建相关文章), B站 出门吃三碗饭,不定期更新视频讲解
接下来我们将依次介绍下面几个坐标
世界坐标,相机坐标,归一化坐标,像素坐标。

首先我们引入一个最简单的相机模型——针孔相机模型
P:真实世界中的一个点
O:相机的光心,处在相机平面上
P‘:真实世界的点通过光心在成像平面上形成的一个点
在左边的平面看作是相机内部的成像平面
光心O到成像平面O‘的距离叫f 焦距
P到光心O的距离w设为z
设P坐标 [X,Y,Z]^T
设P’坐标 [X‘,Y‘,Z‘]^T
z和f的距离可以见右图,通过相似三角形可以得出

我们知道成像平面最终呈现给我们是一张图片,也就是只有2维的信息,于是我们在 成像平面上引入 像素平面,并在其左上角顶点设立起点坐标系,设P’的像素坐标为 [u,v]^T
像素坐标系相对于成像平面,可看做在u、v轴分别缩放了α和β倍,同时原点平移了
[Cx,Cy]^T,像素坐标推导如下图:


为了更加美观,我们把像素坐标变为齐次形式,并写为以上形式
Z:世界空间点到光心距离
K:相机内参矩阵(可以问厂家or自己测;相机如果碰损会影响值)
P:世界空间点的坐标
现在我们已经成功实现了一个数学模型,输入空间的一个点,就输出其通过相机的像素点,是不是很神奇?如果输入的是很多个点,那么最终就会输出一幅色彩丰富的图片啦。
但是,现在我们还有一点要考虑。在上面我们输入的P是相机坐标下的点坐标,但因为相机的运动关系,P的相机坐标应该是其世界坐标P_world,简称P_w ,根据相机位姿变化的结果。
(也就是说如果需要使用P相机坐标,我们需要知道他的值,可以通过P_w推出)
相机的位姿由他的旋转矩阵R和平移向量t来确定,将其代入上述公式,代替P

现在,我们得到了式子,他的含义是:
输入 世界坐标下的点P_w, 先左乘 相机内参矩阵,再右乘 相机外参矩阵T,
值=空间点坐标距离光心距离 右乘 像素坐标
输出:(Z已知)可以得到其 像素坐标
这样,我们的空间点在相机的成像过程就顺利理顺了!
从另一个角度再看,
我们先把世界坐标点P_w转为P相机坐标系点,再除去其最后一维值,也就是Z(该点距离相
机成像平面的深度),这样相当于对最后一个维度归一化(最后一维经过上面操作后变为1),于是我们得到 相机坐标系的点P在 相机归一化平面上的投影点。

归一化坐标可以看作相机前面z=1处的平面有一个点,z=1的平面可以看作归一化平面,归一化坐标左乘内参就得到了像素坐标,因此,我们可以把像素坐标看作是对归一化平面上点量化测量的结果。
这里,如果我们对相机坐标P乘任意非0常数,其归一化坐标都是一样的,也即该点的深度在投影失去了信息。因此单目视觉(针孔成像)没法得到像素点的深度值。该任务需要双目模型来完成。
另外,本篇文章参考借鉴了高翔的视觉SLAM14讲,第5章节,想了解更多细节请自行搜索。
最后,觉的有帮助的话可以关注公众号 AI知识物语, B站 出门吃三碗饭,不定期更新视频讲解。
好了,我去复习明天下午的操作系统考试了,我真的会谢!
相关文章:

针孔成像模型零基础入门(三)
2020年爆火的Nerf(神经辐射场)横空出世,据说只要用手机拍照,然后喂给模型,就可以生成3D模型了,我试过了,确有此事! 那我们有想过,为什么可以从二维的图片里面获取物体三…...

你真的了解环形队列吗?(学习数据结构必须掌握的模型)
目录 0.前言 1. 什么是环形队列 2. 如何使用数组结构 / 链表结构 对环形队列封装 3. 代码手撕环形队列各个接口 3.1 代表封装一个环形队列 3.2 环形队列的初始化 3.3 环形队列的插入 3.4环形队列的删除 3.5环形队列的判空 3.6环形队列的判满 3.7环形队列的队头 3.8环…...

《痞子衡嵌入式半月刊》 第 72 期
痞子衡嵌入式半月刊: 第 72 期 这里分享嵌入式领域有用有趣的项目/工具以及一些热点新闻,农历年分二十四节气,希望在每个交节之日准时发布一期。 本期刊是开源项目(GitHub: JayHeng/pzh-mcu-bi-weekly),欢迎提交 issue,…...
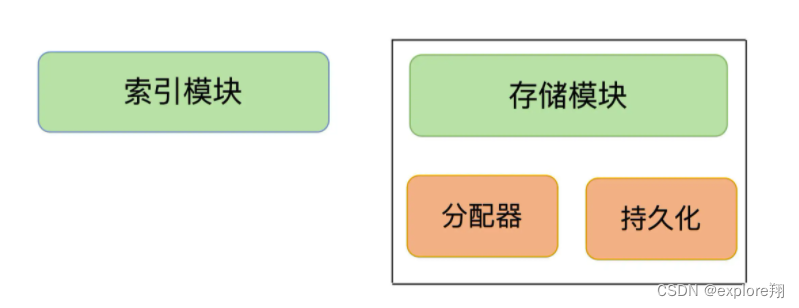
对redis之键值型数据库的理解
键值数据库,首先就要考虑里面可以存什么样的数据,对数据可以做什么样的操作,也就是数据模型和操作接口。它们看似简单,实际上却是我们理解 Redis 经常被用于缓存、秒杀、分布式锁等场景的重要基础。理解了数据模型,你就…...

Linux内核中的软中断、tasklet和工作队列
软中断、tasklet和工作队列并不是Linux内核中一直存在的机制,而是由更早版本的内核中的“下半部”(bottom half)演变而来。下半部的机制实际上包括五种,但2.6版本的内核中,下半部和任务队列的函数都消失了,…...
【Java】Spring Boot 2 集成 nacos
官方文档:https://nacos.io/zh-cn/docs/quick-start-spring-boot.html pom 本次Springboot版本 2.2.6.RELEASE,nacos-config 版本 0.2.7,nacos-discovery版本 0.2.7 parent <parent><groupId>org.springframework.boot</gr…...
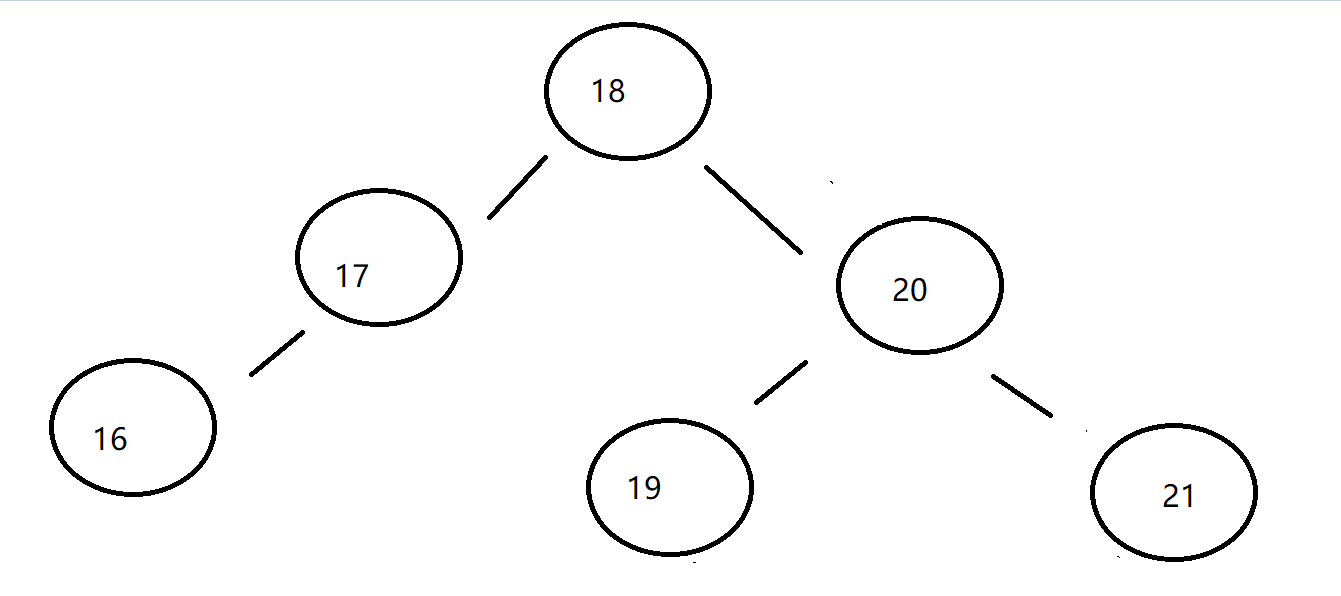
JavaSE学习笔记day14
二、Set Set集合是Collection集合的子接口,该集合中不能有重复元素!! Set集合提供的方法签名,与父接口Collection的方法完全一致!! 即没有关于下标操作的方法 Set接口,它有两个常用的子实现类HashSet,TreeSet 三、HashSet HashSet实现了Set接口,底层是hash表(实际上底层是HashM…...
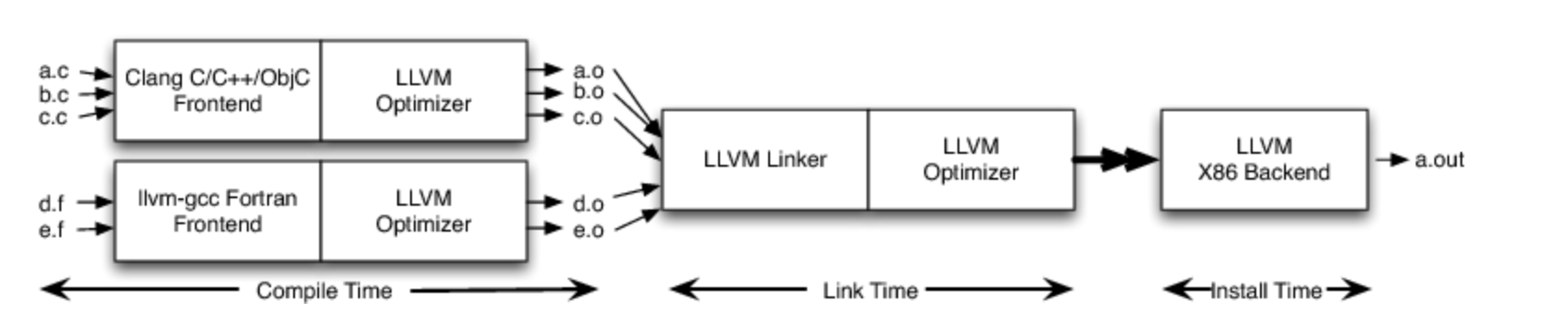
LLVM高级架构介绍
LLVM 为什么要开一个LLVM的新坑呢? 我从智能穿戴转行到芯片软件行业,从事编译器开发,不过是AI编译器。不过基本的传统编译器还是绕不过去啊,所以开始学习LLVM,后面开始学习TVM,MLIR。 LLVM GitHub地址 L…...

全网最经典函数题型【详解】——C语言
文章目录1. 写一个函数可以判断一个数是不是素数。2. 写一个函数判断一年是不是闰年。3. 写一个函数,实现一个整形有序数组的二分查找。4. 写一个函数,每调用一次这个函数,就会将 num 的值增加1。5. 写一个函数,打印乘法口诀表。6…...
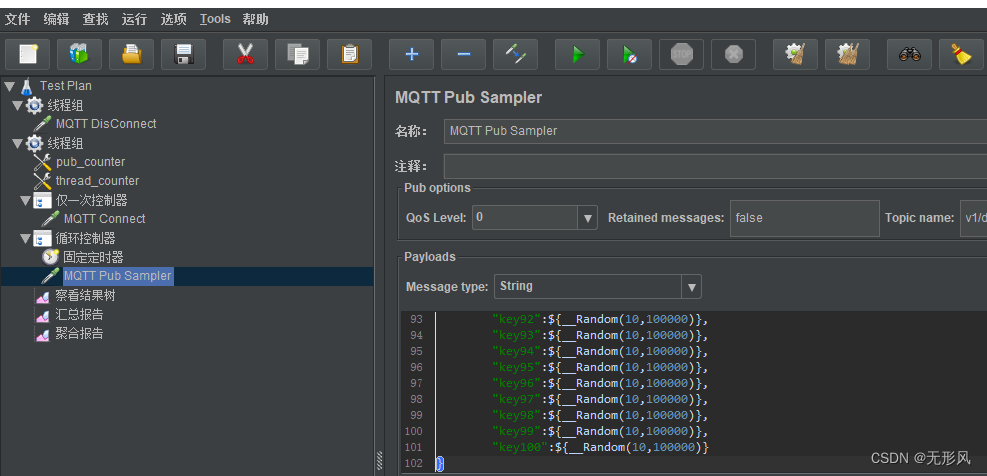
emqx桥接配置+常见问题解决+jmeter压测emqx
一,桥接资源配置及规则配置 Emqx桥接配置流程 1,配置资源并测试连接通过 规则引擎——>资源——>新建——>选择MQTT Bridge——>填写参数测试连接 参数描述详见3.1资源配置 2,配置规则 2.1根据实际业务选择合适sql 规则引擎…...
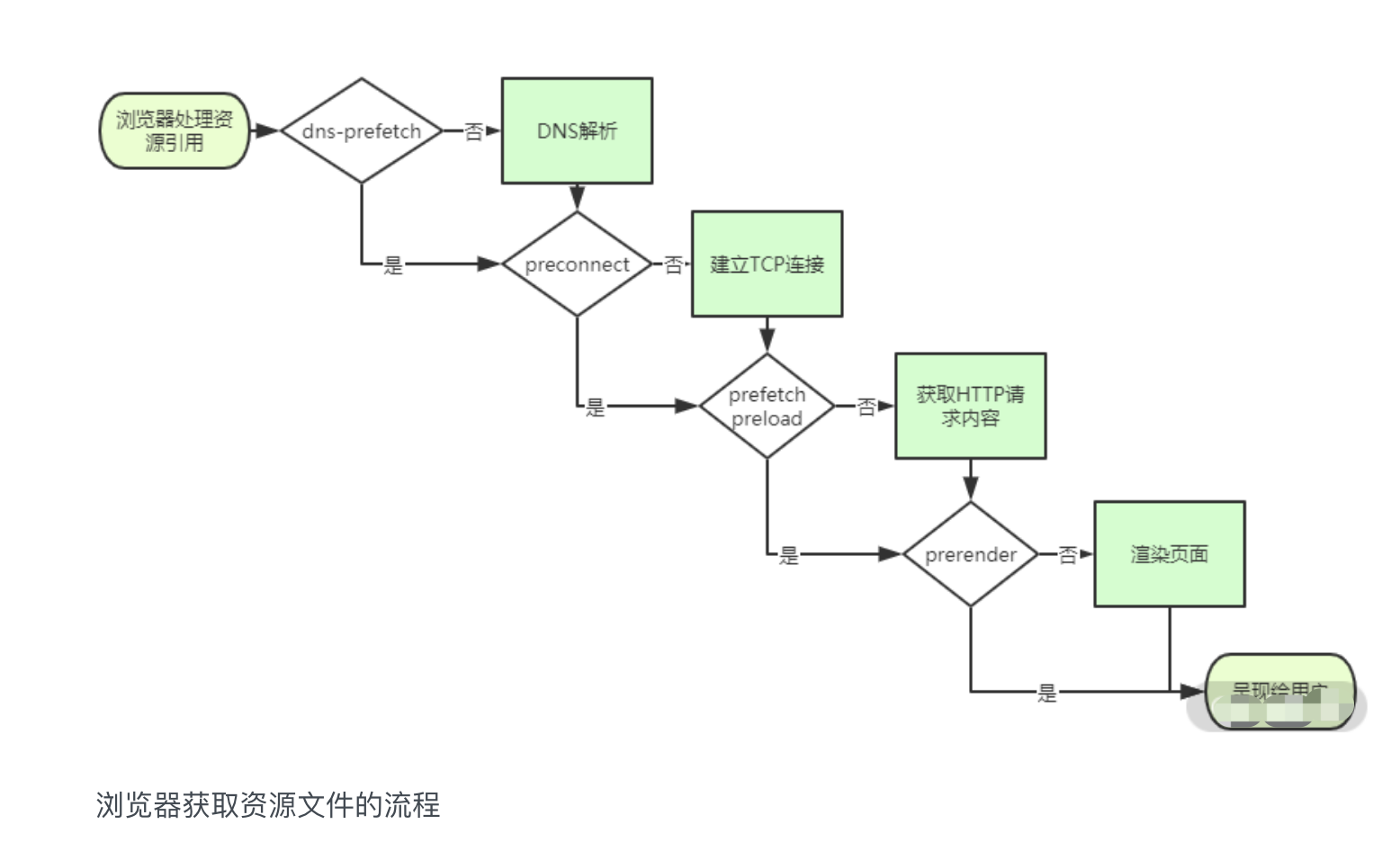
improve-1
类型及检测方式 1. JS内置类型 JavaScript 的数据类型有下图所示 其中,前 7 种类型为基础类型,最后 1 种(Object)为引用类型,也是你需要重点关注的,因为它在日常工作中是使用得最频繁,也是需要…...

华为OD机试用Python实现 -【云短信平台优惠活动】(2023-Q1 新题)
华为OD机试题 华为OD机试300题大纲云短信平台优惠活动题目描述输入描述输出描述示例一输入输出说明示例二输入输出说明Python 代码实现代码编写思路华为OD机试300题大纲 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看…...

Facebook广告投放运营中的关键成功因素是什么?
在当今数字化的时代,广告投放已经成为了各种企业获取市场份额和增加品牌曝光的重要手段之一。Facebook作为全球最大的社交媒体平台之一,其广告投放运营的成功,将直接影响企业的品牌推广和市场营销效果。本文将探讨Facebook广告投放运营中的关…...
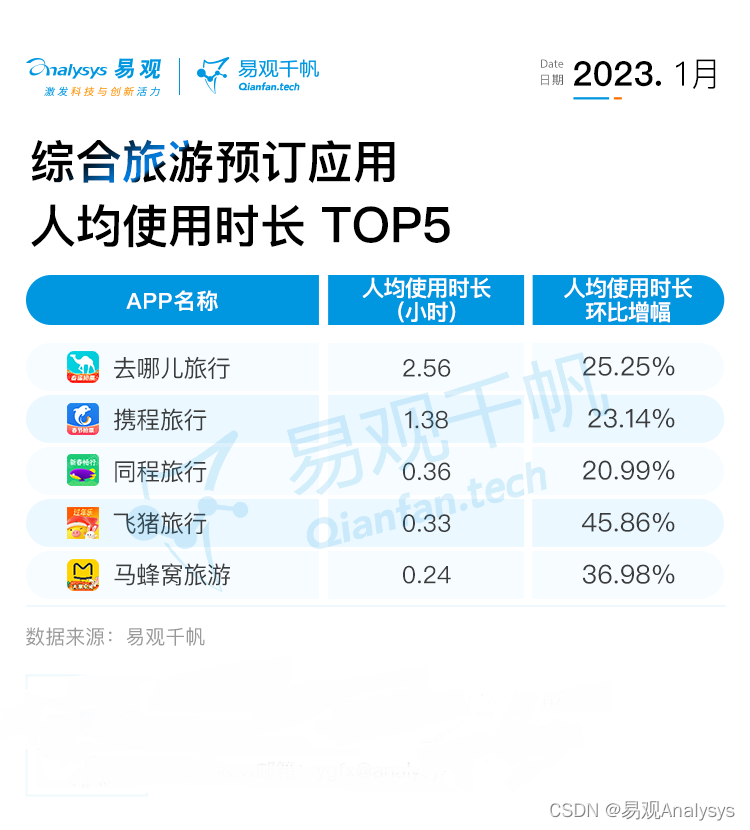
2023年1月综合预订类APP用户洞察——旅游市场复苏明显,三年需求春节集中释放
2023年1月,随着国家对新型冠状病毒感染实施“乙类乙管”,不再对入境人员和货物等采取检疫传染病管理措施,并且取消入境后全员核酸检测和集中隔离,横亘在旅游者与旅游目的地之间的隔阂从此彻底消失。2023年1月恰逢春节假期…...

基于stm32计算器设计
这里写目录标题 完整de代码可q我获取1 系统功能设计2 系统硬件系统分析设计2.1 STM32单片机核心电路设计2.2 LCD1602液晶显示模块电路设计2.3 4X4矩阵键盘模块设计3 STM32单片机系统软件设计3.1 编程语言选择3.2 Keil程序开发环境3.3 FlyMcu程序烧录软件介绍3.4 CH340串口程序烧…...
)
基于SpringCloud的可靠消息最终一致性02:项目骨架代码(上)
在上一节中咱们已经把分布式事务问题交代了一遍,包括两大定理、五大解决方案和一个成熟的开源框架,而咱们最终的目标是用Spring Cloud实现一个实际创业项目的可靠消息最终一致性的分布式事务方案。 先交代一下项目背景。 前几年,社会上慢慢兴起一种称为C2C同城快递的业务,也…...

RockerMQ集群部署
目录一、Broker集群模式1、单Master:2、多Master多Slave模式异步复制3、多Master多Slave模式同步双写二、集群搭建实践1、集群架构2、克隆生成rocketmqos13、修改rocketmqos1配置文件4、克隆生成rocketmqOS25、修改rocketmqOS2配置文件6、启动服务器7、测试一、Brok…...

unicloud的aggregate聚合查询时间戳转日期
我特么不知道看了这个帖子几百遍才看明白到-----》unicloud数据库中,聚合操作如何操作时间戳? - DCloud问答 自己淋过雨老想着为别人撑伞,可怜我这35岁的老人家,给我去点关注!!!!&a…...

Vue2.0开发之——使用ref引用组件实例(41)
一 概述 在本组件内部修改count的值在父组件内修改子组件的count值 二 在本组件内部修改count的值 2.1 Left.vue 布局代码 <template><div class"left-container"><h3 >Left 组件---{{count}}</h3><button click"count 1"&…...

极狐GitLab仓库瘦身
参考文章: [分享] 极狐GitLab仓库瘦身 - 官方技术分享 - 极狐GitLab 论坛 一、瘦身概述 Git仓库随着时间推移会变得越来越大,比如很多比较大的文件加入Git仓库时,可能引起以下问题: 下载仓库越来越慢,因为每个人都…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
