算法第十五期——动态规划(DP)之各种背包问题
目录
0、背包问题分类
1、 0/1背包简化版
【代码】
2、0/ 1背包的方案数
【思路】
【做法】
【代码】
空间优化1:交替滚动
空间优化2:自我滚动
3、完全背包
【思路】
【代码】
4、分组背包
核心代码
5、多重背包
多重背包解题思路1:转化为0/1背包
多重背包解题思路2:直接DP
核心代码
多重背包解题思路3:二进制拆分优化
拆分要点
多重背包解题思路4:单调队列
模板题
【代码】
0、背包问题分类
背包问题可分为0/1背包简化版,背包方案数,完全背包,分组背包,多重背包等
1、 0/1背包简化版
0/1背包的简化版:不管物品的价值。把体积看成最优化目标:最大化体积。
装箱问题 lanqi ao0J题号763
题目描述
有一个箱子容量为 V(正整数,0≤V≤20000),同时有 n 个物品(0≤n≤30),每个物品有一个体积(正整数)。
要求 n 个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。
输入描述
输入第一行,一个整数,表示箱子容量。
第二行,一个整数 n,表示有 n 个物品。
接下来 n 行,分别表示这 n 个物品的各自体积。
输出描述
输出一行,表示箱子剩余空间。
输入输出样例
输入
24 6 8 3 12 7 9 7输出
0
0/1背包的简化版,不管物品的价格。把体积(不是价格)看成最优化目标:最大化体积。
【代码】
dp = [0]*20010
V = int(input())# 容量
n = int(input())# 物品数
c = [0]*40 # 存每个物品体积
# 读入每个物体的体积
for i in range(1, n+1): c[i]=int(input ())
# 自我滚动
for i in range (1, n+1) :for j in range (V, c[i]-1,-1):dp[j] = max(dp[j],dp[j-c[i]]+c[i])
print(V-dp[V]) # 剩余最小容量 = 容量 - 物品最大体积2、0/ 1背包的方案数
2022年届国赛,填空题,langiao0J题号2186
问题描述
将 2022 拆分成 10 个互不相同的正整数之和, 总共有多少种拆分方法?
注意交换顺序视为同一种方法, 例如 2022=1000+1022 和 2022=1022+1000 就视为同一种方法。
答案提交
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
【思路】
- 题目求10个数的组合情况,这十个数相加等于2022。因为是填空题可以不管运行时间,看起来可以用暴力for循环10次,加上剪枝。然而暴力的时间极长,因为答案是:379187662194355221。
- 建模:这一题其实是0/1背包:背包容量为2022,物品体积为1~2022,往背包中装10个物品,要求总体积为2022,问一共有多少种方案。
- 与标准背包的区别:是求方案总数。
【做法】
- 定义dp[ ][ ][ ]: dp[i][i][k]表示数字1~i取j个,容量为k的方案数。
- 下面的分析沿用标准0/1背包的分析方法。
- 从i-1扩展到i,分两种情况:
(1) k>i:数i可以要,也可以不要。
要i: 从1~i-1中取j-1个数,再取i,等价于dp[i-1][j-1][k-i]。
不要i:从1~i-1中取j个数,等价于dp[i-1][i][k]
合起来(要和不要的总方案数): dp[i][i][k] = dp[i-1][i][k] + dp[i-1][j-1][k-i]
( 2) k<i:由于数i比总和k还大,显然i不能用。有: dp[i][i][k]= dp[i-1][ji][k]
【代码】
空间优化1:交替滚动
dp = [[[0]*2222 for i in range(11)] for j in range(2222)] # 比题目要求的数据范围大一点
for i in range(0,2023): dp[i][0][0]=1 # 初始化:递推条件的初始值,不选也是一种方案
for i in range(1,2023):for j in range(1,11):for k in range(1,2023):if k<i: dp[i][j][k] = dp[i-1][j][k]else:dp[i][j][k] = dp[i-1][j][k]+dp[i-1][j-1][k-i]
print(dp[2022][10][2022])空间优化2:自我滚动
dp = [[0]*2222 for i in range(11)]
dp[0][0] = 1 #特别注意这个初始化
for i in range(1,2023):for j in range (10,0,-1): # 10个数for k in range(i,2023): # k>=idp[j][k] += dp[j-1][k-i]
print(dp[10][2022])3、完全背包
- 特点:每种物品有无穷多个
小明的背包2lanqiao0J题号1175
题目描述
小明有一个容量为 V 的背包。
这天他去商场购物,商场一共有 N 种物品,第 i 种物品的体积为 wi,价值为 vi,每种物品都有无限多个。
小明想知道在购买的物品总体积不超过 V 的情况下所能获得的最大价值为多少,请你帮他算算。
输入描述
输入第 1 行包含两个正整数 N,V,表示商场物品的数量和小明的背包容量。
第 2∼N+1 行包含 2 个正整数 w,v,表示物品的体积和价值。
1≤N≤10^3,1≤V≤10^3,1≤wi,vi≤10^3。
输出描述
输出一行整数表示小明所能获得的最大价值。
输入输出样例
输入
5 20 1 6 2 5 3 8 5 15 3 3输出
120
【思路】
和0/1背包类似。0/1背包的每种物品只有1件,完全背包的每种物品有无穷多件,第i种可以装0件、1件、2件、.....、件。
做法:定义dp[i][j]:把前i种物品(从第1种到第i种)装入容量为j的背包中获得的最大价值。把每个dp[i][j]都看成一个背包:背包容量为j,装1~i这些物品。最后得到的dp[N][C]就是问题的答案:把N种物品装进容量C的背包的最大价值。
区别:在0/1背包问题中,每个物品只有拿与不拿两种;而完全背包问题,需要考虑拿几个
【代码】
完全背包的代码和0/1背包的代码相似,只多了一个k循环,用来遍历每种物品拿几个。
def solve(n,C) :for i in range (1, n+1):for j in range (0,C+1):dp[i][j] = dp[i - 1][j] # 初始化为都不装的情况for k in range(1,j//c[i]+1): # 可以拿1~j//c[i]个该物品 k*c[i]<=j #在容量为j的背包中放k个dp[i][j] = max(dp[i][j],dp[i - 1][j - k * c[i]] +k * w[i])return dp[n][C]N = 3011
dp = [[0]*N for j in range(N)]
w =[0]*N; c = [0]*N
n,C = map(int,input().split())
for i in range(1, n+1):c[i], w[i] = map(int,input ().split()) # 每个物品的体积和价值
print(solve(n,C))也可以不需要初始化条件,但下面要从0个该物品开始遍历,这样写代码更加简洁,但时间复杂度高了一点,代码如下:
def solve(n,C) :for i in range (1, n+1):for j in range (0,C+1):dp[i][j] = dp[i - 1][j] # 初始化为都不装的情况for k in range(1,j//c[i]+1): # 可以拿1~j//c[i]个该物品 k*c[i]<=j #在容量为j的背包中放k个dp[i][j] = max(dp[i][j],dp[i - 1][j - k * c[i]] +k * w[i])return dp[n][C]N = 3011
dp = [[0]*N for j in range(N)]
w =[0]*N; c = [0]*N
n,C = map(int,input().split())
for i in range(1, n+1):c[i], w[i] = map(int,input ().split()) # 每个物品的体积和价值
print(solve(n,C))4、分组背包
分组背包问题:
- 有一些物品,把物品分为n组,其中第i组第k个物品体积是c[i][k],价值是w[i][k];
- 每组内的物品冲突,每组内最多只能选出一个物品;
- 给定一个容量为C的背包,问如何选物品,使得装进背包的物品的总价值最大。
解题思路与0/1背包相似。
- 0/1背包dp[i][j]:把前i个物品(从第1个到第i个)装入容量为j的背包中获得的最大价值。
- 分组背包dp[i][j]:把前i组物品装进容量j的背包(每组最多选一个物品),可获得的最大价值。
- 状态转移方程:
dp[i][j] = max {dp[i-1][j],dp[i-1][j-c[i][k]] + w[i][k]} dp[i-1][j]表示第i组不选物品,dp[i-1][j-c[i][k]]表示第i组选第k个物品。 - 求解方程需要做i、j、k的三重循环。
核心代码:
状态转移方程:dp[i][j] = max {dp[i-1][j], dp[i-1][j-c[i][k]] + w[i][k]},用滚动数组,变为:dp[j] = max {dp[j],dp[j-c[i][k]]+ w[i][k]}
dp = [0] * N
for i in range(1, n + 1): # 遍历每个组for j in range(C, -1, -1): # 枚举容量for k in range(1, C + 1): # 用k枚举第i组的所有物品if j >= c[i][k]: # 第k个物品能装进容量j的背包dp[j] = max(dp[j], dp[j - c[i][k]] + w[i][k]) # 第i组第k个
print(dp[C])5、多重背包
多重背包问题:
- 给定n种物品和一个背包,第i种物品的体积是ci,价值为wi,并且有mi个,背包的总容量为C。
- 如何选择装入背包的物品,使得装入背包中的物品的总价值最大?
- 与完全背包的区别:完全背包是每种物品都有无限多个,而多重背包是有限个
多重背包解题思路1:转化为0/1背包
- 转换为0/1背包问题。
- 把相同的
个第i种物品看成独立的
个,总共
个物品,。
- 然后按0/1背包求解,复杂度
。
多重背包解题思路2:直接DP
- 定义状态dpli][j]:表示把前i个物品装进容量j的背包,能装进背包的最大价值。
- 第i个物品分为装或不装两种情况,状态转移方程:
dp[i][j] = max {dp[i-1][j],dp[i-1][j-k*c[i]] +k*w[i]}
1 ≤k ≤min{m[i], j/c[i]} # k不能超过 个和最大容量个数的最小值
- 直接写i、j、k三重循环,复杂度和第一种思路的复杂度一样。
- 对比完全背包:1≤k ≤ j/c[i]
核心代码:
状态转移方程:dp[i][j] = max {dp[i-1][j], dp[i-1][j-k*c[i]]+ k*w[i]},用滚动数组,变为:dp[j] = max{dp[j],dp[j-k*c[i]]+ k*w[i]}。
dp = [0]*N
for i in range(1, n+1): #枚举物品for j in range (C,c[i]-1,-1): #枚举背包容量for k in range(1,m[i]+1): #用k遍历第i组的所有物品if(j >= k*c[i]): #第k个物品能装进容量j的背包dp[j] = max(dp[j], dp[j-k*c[i]]+k*w[i])
print(dp[C])多重背包解题思路3:二进制拆分优化
- 一种简单而有效的技巧。
- 例如第i种物品有
= 25个,这25个物品放进背包的组合,有0~25的26种情况。
- 不过要组合成26种情况,其实并不需要25个物品。
- 根据二进制的计算原理,一个十进制整数X,可以用1、2、4、8、...这些2的倍数相加得到,例如25=16+8+1,这些2的倍数只有logX个。
- 题目中第i种物品有
个,用log
个数就能组合出0 ~
种情况。总复杂度从
优化到
。
拆分要点:
- 注意拆分的具体实现,不能全部拆成2的倍数,而是先按2的倍数从小到大拆,最后是一个小于等于最大倍数的余数。
- 保证拆出的数相加在[1, mi]范围内,不会大于mi。
- 例如mi= 25,把它拆成1、2、4、8、10,最后是余数10,10<16,这5个数能组合成1~25内的所有数字,不会超过25。
- 错误示例:如果把25拆成1、2、4、8、16,相加的范围就是[1,31]了。
多重背包解题思路4:单调队列
因为这一讲主要是讲dp算法,所以就不在直接过多介绍其他算法,但这个方法优化程度更高,有兴趣的朋友可以看看这篇文章:单调队列优化多重背包(全网最详细解析)
模板题
【输入描述】第一行是整数n和C,分别表示物品种数和背包的最大容量。接下来 n行,每行三个整数 wi、ci、mi,分别表示第i个物品的价值、体积、数量。
【输出描述】输出一个整数,表示背包不超载的情况下装入物品的最大价值。
【输入样例】
4 20
3 9 3
5 9 1
9 4 2
8 1 3
【输出样例】
47
【代码】
代码用二进制拆分优化来解答。
N = 100010
w = [0] * N;c = [0] * N;m = [0] * N
xw = [0] * N;xc = [0] * N # 经过二进制拆分后的新体积和新价值,转换后每个物体只有一个,所以没有新的数量n, C = map(int, input().split())
for i in range(1, n + 1):w[i], c[i], m[i] = map(int, input().split())# 以下是二进制拆分
xn = 0 # 二进制拆分后的新物品总数量
for i in range(1, n + 1):j = 1while j <= m[i]: # 例:直到最后一个数m[i](余数)出现m[i] -= j # 减去已拆分的xn += 1xc[xn] = j * c[i] # 新物品的体积xw[xn] = j * w[i]j <<= 1 # 二进制枚举:1,2,4...if m[i] > 0: # 最后一个是余数xn += 1xc[xn] = m[i] * c[i]xw[xn] = m[i] * w[i]
# 以下是滚动数组版本的0/1背包
dp = [0] * N
for i in range(1, xn + 1): # 枚举物品for j in range(C, xc[i] - 1, -1): # 枚举背包容量 xc[i] - 1这里的-1是因为range函数是左闭右开区间,-1才能取到xc[i]dp[j] = max(dp[j], dp[j - xc[i]] + xw[i])
print(dp[C])相关文章:
算法第十五期——动态规划(DP)之各种背包问题
目录 0、背包问题分类 1、 0/1背包简化版 【代码】 2、0/ 1背包的方案数 【思路】 【做法】 【代码】 空间优化1:交替滚动 空间优化2:自我滚动 3、完全背包 【思路】 【代码】 4、分组背包 核心代码 5、多重背包 多重背包解题思路1:转化…...
实现复选框全选和全不选的切换
今天,复看了一下JS的菜鸟教程,发现评论里面都是精华呀!! 看到函数这一节,发现就复选框的全选和全不选功能展开了讨论。我感觉挺有意思的,尝试实现了一下。 1. 全选、全不选,两个按钮ÿ…...
React hooks之useState用法(一)
系列文章目录 学习React已经有很长的一段时间了,今天决定重新回顾一下跟React相关的一些知识点 文章目录系列文章目录结构如下一、hooks是什么?useState可以能做什么二、如何使用useState()第一步:创建【函数组件&…...
spring的简单理解
目录 1 .ioc容器(控制反转) 2. Aop面向切面编程 3. 事务申明 4. 注解的方式启动 5. spring是什么与他的优势 6. 代理设计模式(比如aop) 7. springmvc中相应json数据 8. 使用lombok来进行对代码的简化 9. 使用logback记录…...
Docker调用Intel集显实现FFmpeg硬解码
文章目录Docker调用Intel集显实现FFmpeg硬解码参考FFmpeg 集成qsv方式一 容器完成所有步骤方式二 容器完成部分步骤方式三 dockerfile部署Docker调用Intel集显实现FFmpeg硬解码 参考 ffmpeg_qsv_docker拉取该镜像可以实现FFmpeg集成vaapi的硬加速,通过dockerfile文…...

端到端模型(end-to-end)与非端到端模型
一、端到端(end to end) 从输入端到输出端会得到一个预测结果,将预测结果和真实结果进行比较得到误差,将误差反向传播到网络的各个层之中,调整网络的权重和参数直到模型收敛或者达到预期的效果为止,中间所…...
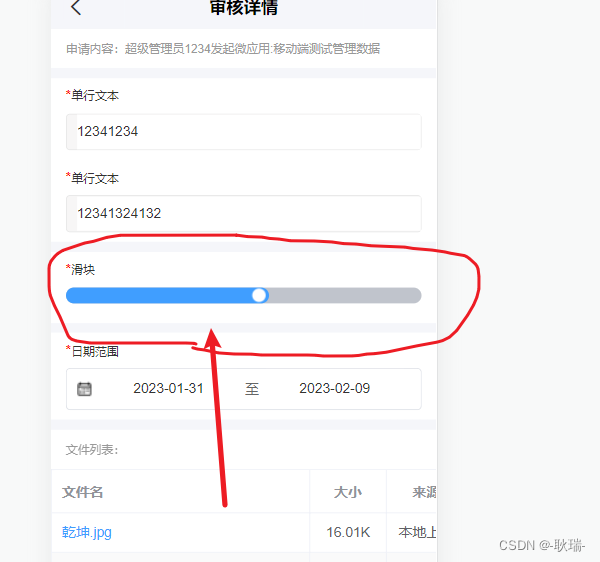
uniApp封装一个滑块组件
最近 项目中有一个需求 PC端动态设计的表单 移动端要能渲染出来 那么 就要去找到对应的组件 而其中 没有的 就包括滑块 没有又能怎么办 只能自己封装一个 我们直接上代码 <template><view class"u-slider" tap"onClick" :class"[disabled…...

运动基元(二):贝塞尔曲线
贝塞尔曲线是我第一个深入接触并使用于路径规划的运动基元。N阶贝塞尔曲线具有很多优良的特性,例如端点性、N阶可导性、对称性、曲率连续性、凸包性、几何不变性、仿射不变性以及变差缩减性。本章主要介绍贝塞尔曲线用于运动基元时几个特别有用的特性。 一、贝塞尔曲线的定义 …...

Android 11.0 关于Launcher3中调用截图功能总是返回null的解决方案
1.1概述 在11.0的系统产品开发中,在某些时候需要调用截图接口来进行截屏功能实现,而在Launcher3中发现调用系统截屏接口SurfaceControl.screenshot进行截图的时候始终为null, 获取不到系统当前页面的截屏功能,所以需要找到当前截屏失败的原因然后来实现截屏功能的实现,下面来…...

random随机数
random随机数 1.概述 random用来生成一些随机数,下面介绍random模块提供的方法根据需求生成不同的随机数。 2.random常用操作 2.1.random默认随机数 random()函数返回一个随机的浮点值,默认返回值范围在0 < n < 1.0区间 import randomfor i …...
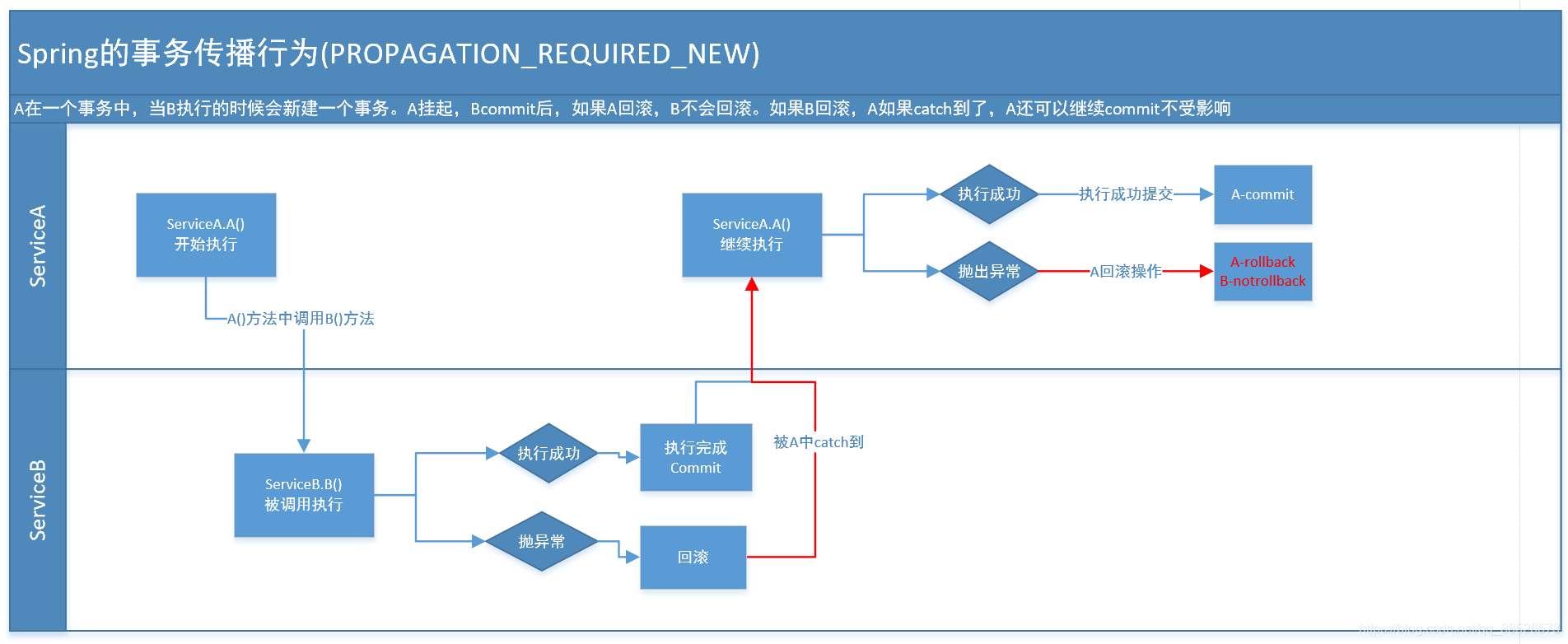
【金三银四系列】Spring面试题-上(2023版)
Spring面试专题 1.Spring应该很熟悉吧?来介绍下你的Spring的理解 有些同学可能会抢答,不熟悉!!! 好了,不开玩笑,面对这个问题我们应该怎么来回答呢?我们给大家梳理这个几个维度来回答 1.1 Spring的发展历程 先介绍…...

linux基本功系列之tar命令实战
文章目录前言一. tar命令介绍二. 语法格式及常用选项三. 参考案例3.1 仅打包不压缩3.2 打包后使用调用压缩命令进行压缩3.3 列出文件的内容3.4 追加文件到tar命令中3.5 释放文件到指定的目录四 . 各种压缩方式的比较总结前言 大家好,又见面了,我是沐风晓…...
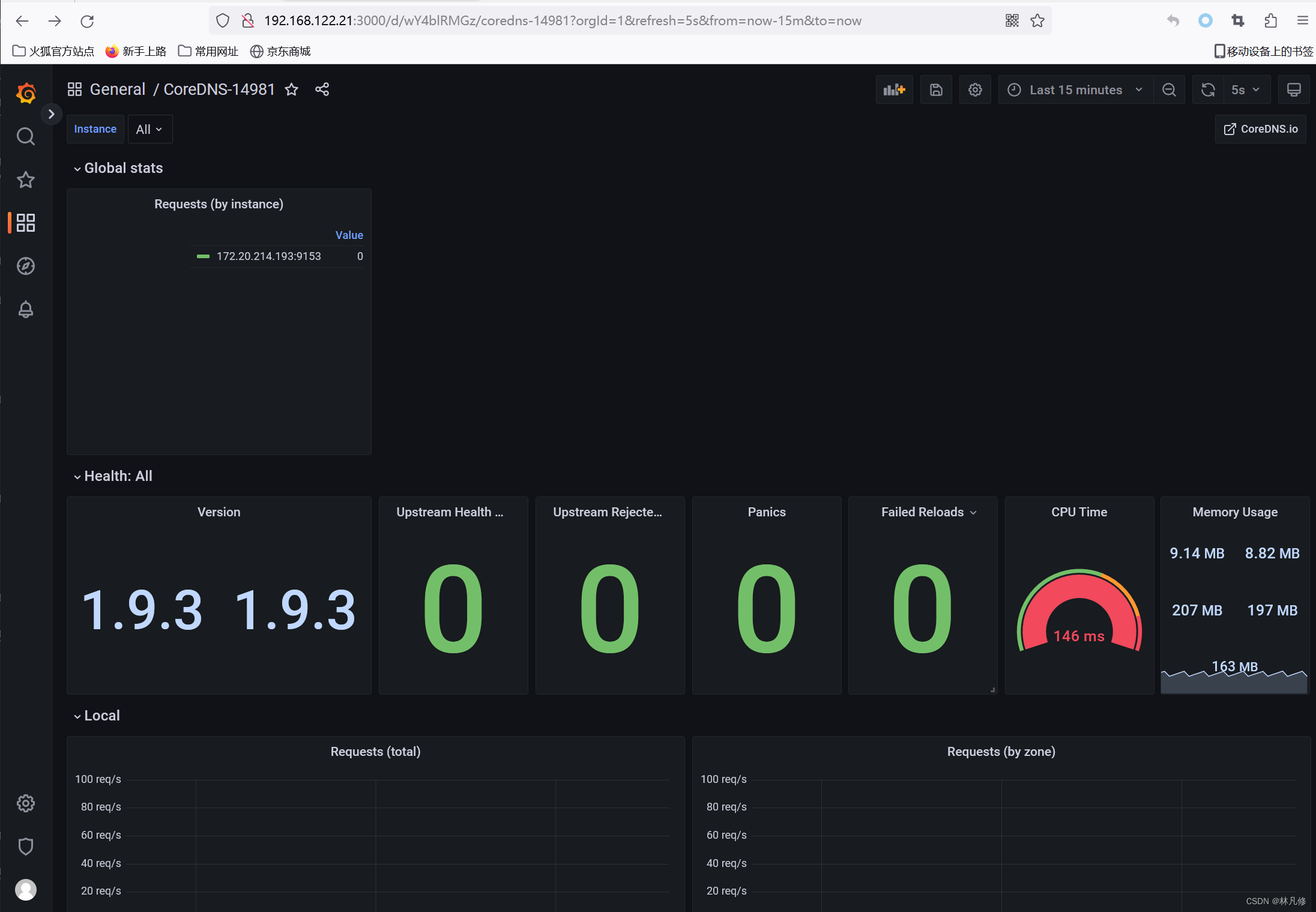
Prometheus服务发现
Prometheus服务发现介绍 Prometheus默认是采用pull的方式拉取监控数据的,每一个被抓取的目标都要暴露一个HTTP接口,prometheus通过这个接口来获取相应的指标数据,这种方式需要由prometheus-server决定采集的目标服务器有哪些,通过…...
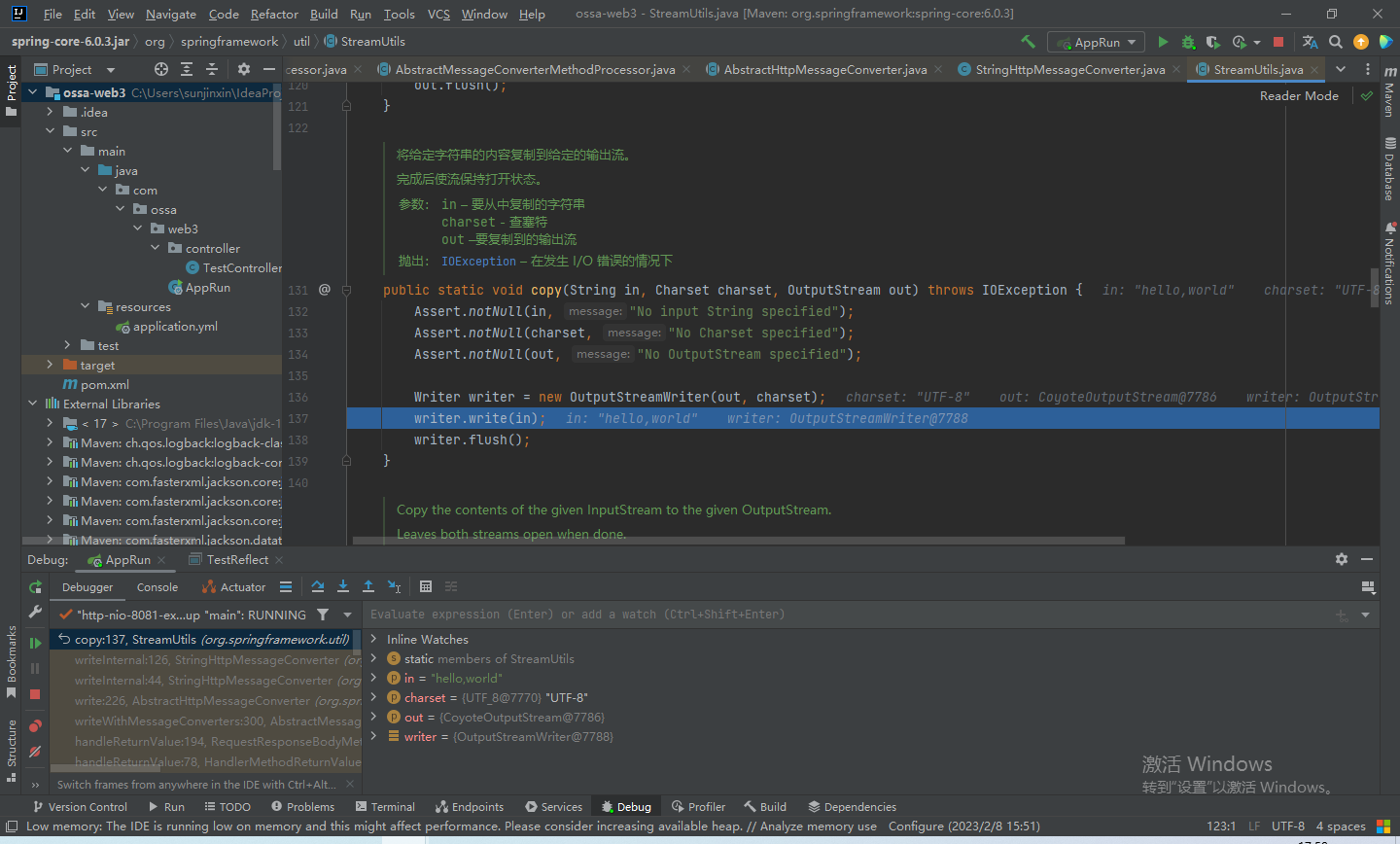
【Spring6源码・MVC】请求处理流程源码解析
上一篇《【Spring6源码・MVC】初始化registry,完成url和controller的映射关系》我们知道,在IOC容器加载的同时,初始化了registry这个HashMap,这个HashMap中存放了请求路径和对应的方法。当我们请求进来,会通过这个regi…...

elasticsearch term match 查询
1. 准备数据 PUT h1/doc/1 {"name": "rose","gender": "female","age": 18,"tags": ["白", "漂亮", "高"] }PUT h1/doc/2 {"name": "lila","gender&quo…...
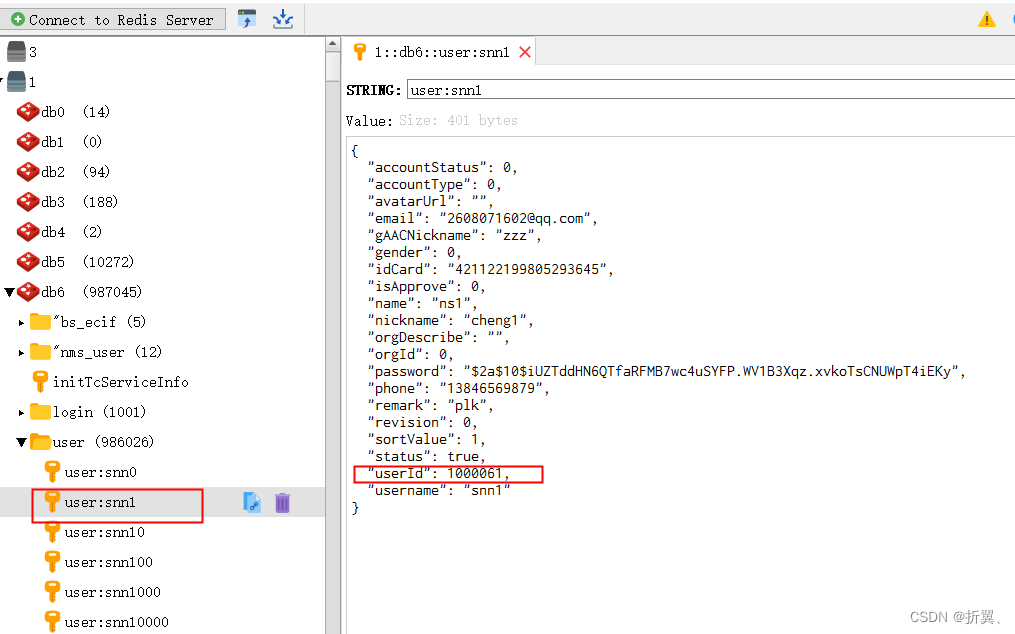
canal使用说明:MySQL、Redis实时数据同步
1. canal简介 canal是阿里开源的数据同步工具,基于bin log可以将数据库同步到其他各类数据库中,目标数据库支持mysql,postgresql,oracle,redis,MQ,ES等 canal分成服务端deployer和客户端adapter,我们可以部署多个,同时为了方便管…...

计算机视觉框架OpenMMLab开源学习(三):图像分类实战
前言:本篇主要偏向图像分类实战部分,使用MMclassification工具进行代码应用,最后对水果分类进行实战演示,本次环境和代码配置部分省略,具体内容建议参考前一篇文章:计算机视觉框架OpenMMLab开源学习&#x…...

awk命令
一.介绍 awk是专门为文本处理设计的编程语言,是一门数据驱动的编程语言。与sed类似,都是以数据驱动的行处理软件,主要用于数据扫描,过滤和汇总。数据可以来自于标准输入,管道或者文件。 二.语法 awk是一种处理文本文件…...

LocalDateTime获取时间的年、月、日、时、分、秒、纳秒
如何把String/Date转成LocalDateTime参考String、Date与LocalDate、LocalTime、LocalDateTime之间互转 String、Date、LocalDateTime、Calendar与时间戳之间互相转化参考String、Date、LocalDateTime、Calendar与时间戳之间互相转化 方法介绍 getYear() 获取日期的年 getMon…...
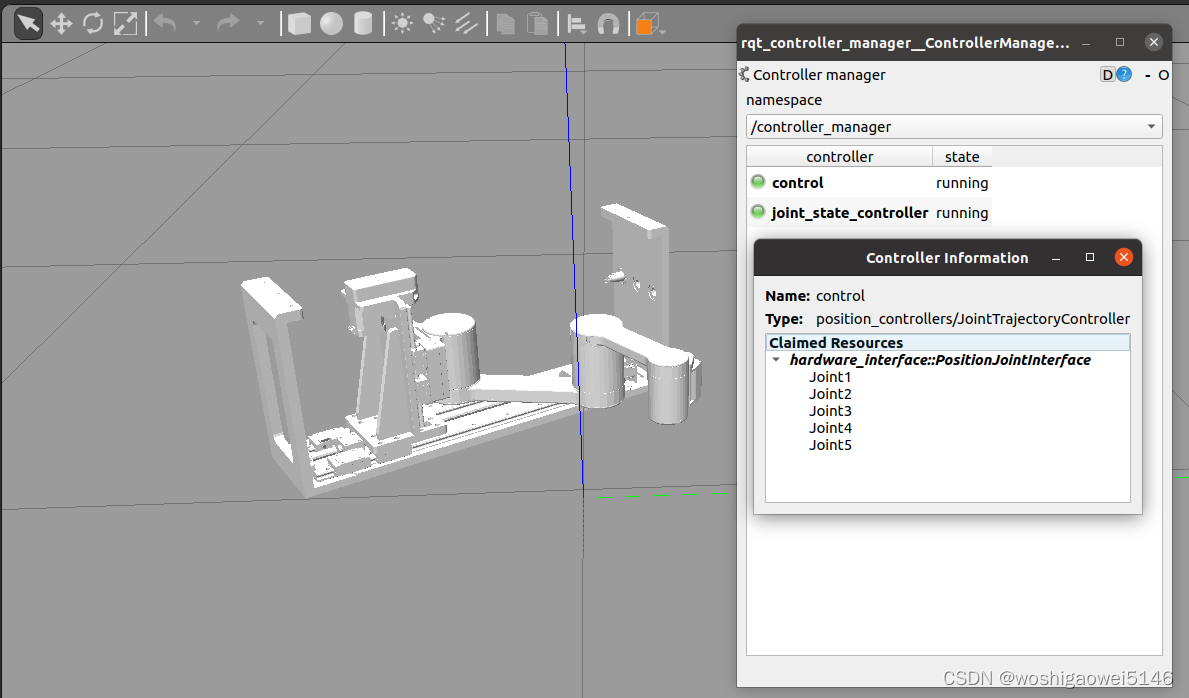
MoveIT Rviz和Gazebo联合仿真
文章目录环境安装概述ros_control框架ros_control数据流文件配置附加工具故障问题解决参考接前两篇:ROS MoveIT1(Noetic)安装总结 Solidworks导出为URDF用于MoveIT总结(带prismatic) MoveIT1 Assistant 总结 环境 Ubu…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

21-Oracle 23 ai-Automatic SQL Plan Management(SPM)
小伙伴们,有没有迁移数据库完毕后或是突然某一天在同一个实例上同样的SQL, 性能不一样了、业务反馈卡顿、业务超时等各种匪夷所思的现状。 于是SPM定位开始,OCM考试中SPM必考。 其他的AWR、ASH、SQLHC、SQLT、SQL profile等换作下一个话题…...

从0开始学习R语言--Day17--Cox回归
Cox回归 在用医疗数据作分析时,最常见的是去预测某类病的患者的死亡率或预测他们的结局。但是我们得到的病人数据,往往会有很多的协变量,即使我们通过计算来减少指标对结果的影响,我们的数据中依然会有很多的协变量,且…...
