【POJ 3352】Road Construction 题解(Tarjan算法求边双连通分量缩点)
描述
现在几乎是夏天,这意味着几乎是夏天的施工时间!今年,负责偏远岛热带岛屿天堂道路的好心人希望修复和升级岛上各个旅游景点之间的各种道路。
道路本身也很有趣。由于岛上的奇怪风俗,道路的安排使得它们不会在交叉路口相遇,而是通过桥梁和隧道相互交叉或下方。通过这种方式,每条道路在两个特定的旅游景点之间穿行,这样游客就不会无法挽回地迷路。
不幸的是,考虑到每条道路所需的维修和升级的性质,当建筑公司在某条道路上施工时,这条道路在任何方向都无法使用。如果无法在两个旅游景点之间旅行,即使建筑公司在任何特定时间只在一条道路上施工,这可能会造成问题。
因此,偏远岛屿的公路部门决定请您的咨询服务来帮助解决这个问题。已决定在各个景点之间修建新的道路,以便在最终配置中,如果任何一条道路正在施工,则仍可以使用剩余的道路在任何两个旅游景点之间行驶。您的任务是找到所需的最少数量的新道路。
输入
第一行输入由正整数n和r组成,用空格隔开,其中3≤n≤1000是岛上旅游景点的数量,2≤r≤1000是道路的数量。旅游景点的标记很方便,从1到n。以下r行中的每一行将由两个整数v和w组成,用空格隔开,表示标记为v和w的景点之间存在一条道路。请注意,您可以沿着每条道路向任何方向行驶,任何一对旅游景点之间最多只能有一条道路直接连接。此外,您可以放心,在当前配置中,您可以在任意两个旅游景点之间旅行。
输出
一行,由一个整数组成,它给出了我们需要添加的最小道路数。
Sample Input
Sample Input 1
10 12
1 2
1 3
1 4
2 5
2 6
5 6
3 7
3 8
7 8
4 9
4 10
9 10
Sample Input 2
3 3
1 2
2 3
1 3
Sample Output
Output for Sample Input 1
2
Output for Sample Input 2
0
Source
CCC 2007
思路
用Tarjan算法求边双连通分量缩点,每两个度为1的叶子节点添加一条边。
AC代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#define AUTHOR "HEX9CF"
using namespace std;const int maxn = 100005;int cnt;
struct Snode {int to;int next;
}edge[maxn];
int head[maxn];// tarjan
int num;
int dfn[maxn], low[maxn];
int deg[maxn];void init(){cnt = 0;num = 0;memset(head, -1, sizeof(head));memset(dfn, 0, sizeof(dfn));memset(low, 0, sizeof(low));memset(deg, 0, sizeof(deg));
}void add(int u, int v){edge[cnt].to = v;edge[cnt].next = head[u];head[u] = cnt++;
}void print(int x){for(int j = 1; j <= x; j++){cout << j << "-";for(int i = head[j]; ~i; i = edge[i].next){cout << edge[i].to;}cout << endl;}
}void tarjan(int u, int root){dfn[u] = low[u] = ++num;for (int i = head[u]; ~i; i = edge[i].next){int v = edge[i].to;if (v == root){continue;}if(!dfn[v]){tarjan(v, u);low[u] = min(low[u], low[v]);}else{low[u] = min(low[u], dfn[v]);}}}int main() {int n, r, si;while(cin >> n >> r){init();for(int i = 0; i < r; i++){int u, v;cin >> u >> v;add(u, v);add(v, u);}// print(r);for(int i = 1; i <= r; i++){if(!dfn[i]){tarjan(i,i);}}// 求缩点和度for(int u = 1; u <= n; u++){for(int i = head[u]; ~i; i = edge[i].next){int v = edge[i].to;if(low[u] != low[v]){deg[low[u]]++;}}}// 统计叶子数int leaf = 0;for(int i = 1; i <= n; i++){if(1 == deg[i]){leaf++;}}// 每两个叶子间加一条路cout << (leaf + 1) / 2 << endl;}return 0;
}
相关文章:
)
【POJ 3352】Road Construction 题解(Tarjan算法求边双连通分量缩点)
描述 现在几乎是夏天,这意味着几乎是夏天的施工时间!今年,负责偏远岛热带岛屿天堂道路的好心人希望修复和升级岛上各个旅游景点之间的各种道路。 道路本身也很有趣。由于岛上的奇怪风俗,道路的安排使得它们不会在交叉路口相遇&…...
Python—单分支结构
(1)if分支语句 Python中if语句的语法结构: if <条件表达式>: 满足条件运行的代码1 满足条件运行的代码2 代码示例: age 12 if age > 18:print(去上网)if 1 1 2 and :print(我满足条件了)if 1 …...
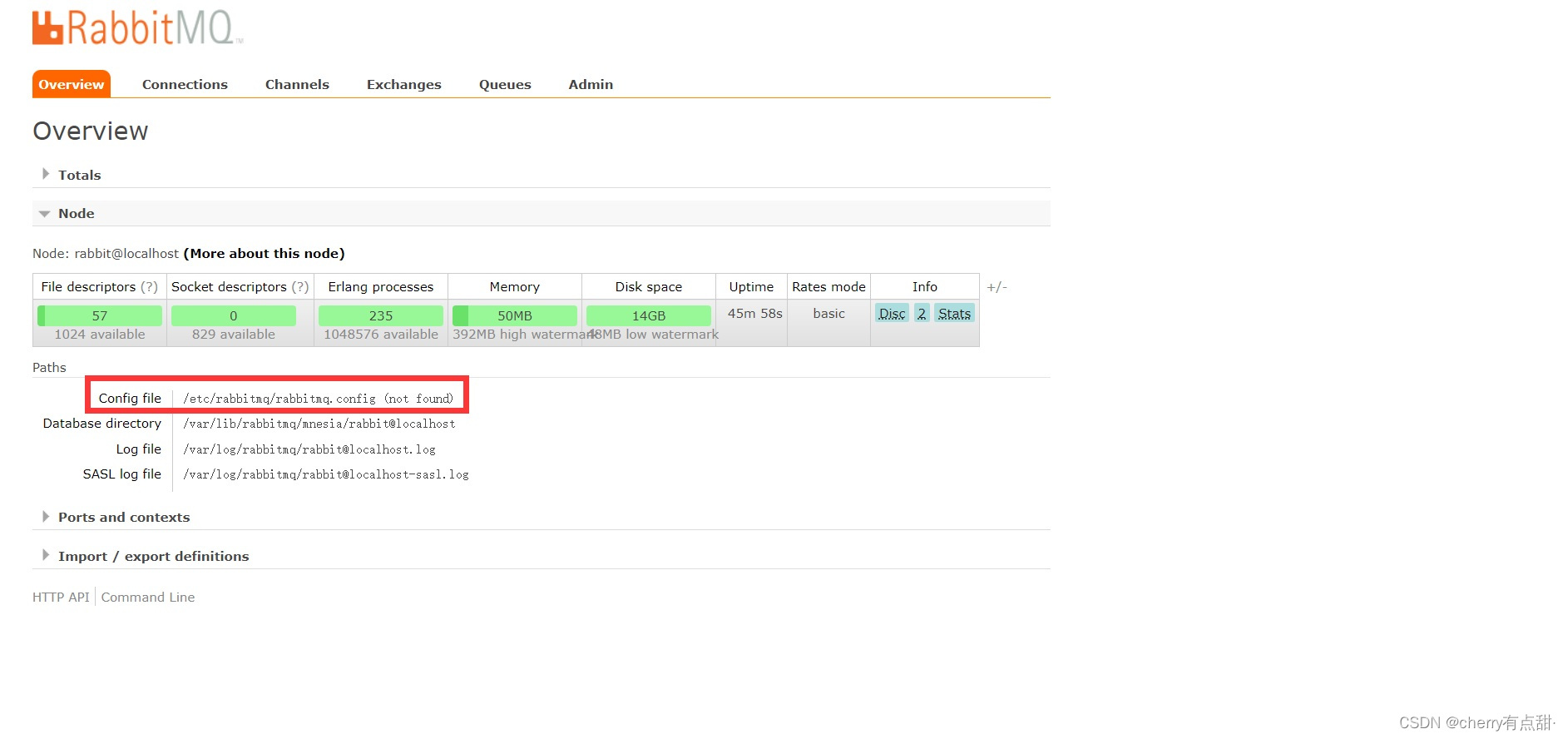
rabbitmq添加用户,虚拟机步,设置rabbitmq配置文件
第一步,登录后台控制页面 http://ip:15672第二步,添加用户和权限 重点:选择Admin和Users 第三步,添加虚拟机 点击侧边的Virtual Hosts 第四步将虚拟机和用户搭配 注意新建好后,在虚拟机列表中,点击虚拟机…...

Codeforces Round#853 div2 A-C
Codeforces Round#853 div2 A-C 等了很久终于迎来了一场cf比赛,白天出去玩了一圈,晚上回来打比赛,这次只出了A,B题。C题思路很巧妙,赛时没做出来,看了大佬学习到了,还是很不错。 A.Serval and Mocha’s A…...
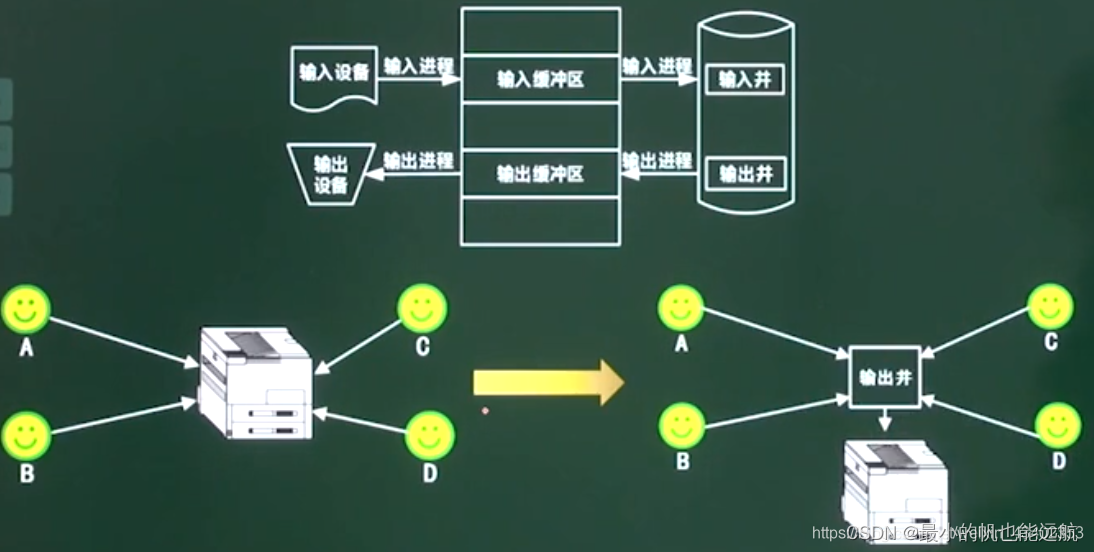
软考之操作系统知识
目录 1.进程管理-进程的概念 2.进程的三态图和五态图 3.进程的同步与互斥 4.PV操作应用 5.死锁问题 6.银行家算法 7.存储管理 8.段式存储组织 9.段页式存储组织 10.页面置换算法 11.磁盘管理 12.作业管理 13.索引文件结构 14.树型目录结构 15.空闲存储空间管理 …...

【线性代数/计算复杂性理论】积和式的指数时间算法:Ryser算法
文章目录一、积和式的定义二、Ryser算法三、代码实现一、积和式的定义 积和式(permanent)是一种和行列式长得很像的矩阵函数。在介绍积和式之前,我们先看看行列式(determinant)的定义。 首先需要引入“排列”&#x…...

代码随想录 NO52 | 动态规划_leetcode 647. 回文子串 516.最长回文子序列
动态规划_leetcode 647. 回文子串 516.最长回文子序列今天是动态规划最后一天的题了,整个过程已经接近尾声了! 647. 回文子串 确定dp数组(dp table)以及下标的含义 本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp…...
【数据挖掘】1、综述:背景、数据的特征、数据挖掘的六大应用方向、有趣的案例
目录一、背景1.1 学习资料1.2 数据的特征1.3 数据挖掘的应用案例1.4 获取数据集1.5 数据挖掘的定义二、分类三、聚类四、关联分析五、回归六、可视化七、数据预处理八、有趣的案例8.1 隐私保护8.2 云计算的弹性资源8.3 并行计算九、总结一、背景 1.1 学习资料 推荐书籍如下&a…...
【架构师】零基础到精通——康威定律
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小留言…...

Could not extract response: no suitable HttpMessageConverter
版本:spring-cloud-openfeign-core-2.1.1.RELEASE.jar,spring-webmvc-5.1.14.RELEASE.jar,jetty-server-9.4.41.v20210516.jar,tomcat-embed-core-9.0.48.jar 问题背景 生产服务请求下游服务时偶发抛出下面的异常,下…...

文献计量三大定律之一---洛特卡定律及普赖斯定律
科学生产率是洛特卡定律的基础,科学生产率”(Scientific Productivity))是指科学家(科研人员)在科学上所表现出的能力和工作效率,通常用其生产的科学文献的数量来衡量。 1926年,洛特卡在一篇论文中提出了科…...
2023年软考高级网络规划设计师
网络规划设计师是软考高级考试科目之一,也是比较难的科目,据官方数据统计网规每年的通过率很低,而且每年只有下半年11月份考一次,如果是直接裸考,估计很悬哦~ 但是你参加考试获得证书的过程就是一个学习网络规划系统知…...

数据治理驱动因素 -报考题
数据治理并不是到此为止,而是需要直接与企业战略保持一致。数据治理越显著地帮助解决组织问题,人们越有可能改变行为、接受数据治理实践。数据治理的驱动因素大多聚焦于减少风险或者改进流程。(1)减少风险1)一般性风险…...
2023淘宝天猫38节红包满减优惠活动时间是从几月几号什么时候开始?
2023年淘宝天猫38节活动将于2023年3月2日中午12点正式开始,活动将持续至2023年3月8日晚上23点59分。届时,淘宝天猫将推出一系列的优惠活动和红包福利,为广大女性用户送上节日的祝福和福利。在这个特别的节日里,淘宝天猫为女性用户…...
、数据压缩、存储优化)
Hive表优化、表设计优化、Hive表数据优化(ORC)、数据压缩、存储优化
文章目录Hive表优化Hive表设计优化分区表结构 - 分区设计思想分桶表结构 - Join问题Hive中的索引Hive表数据优化常见文件格式TextFileSequenceFileParquetORC数据压缩存储优化 - 避免小文件生成存储优化 - 合并输入的小文件存储优化 - ORC文件索引Row Group IndexBloom Filter …...

LearnOpenGL-入门-着色器
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject LearnOpenGL中文官网:https://learnopengl-cn.github.io/ 文章目录着色器GLSL数据类型输入与输…...
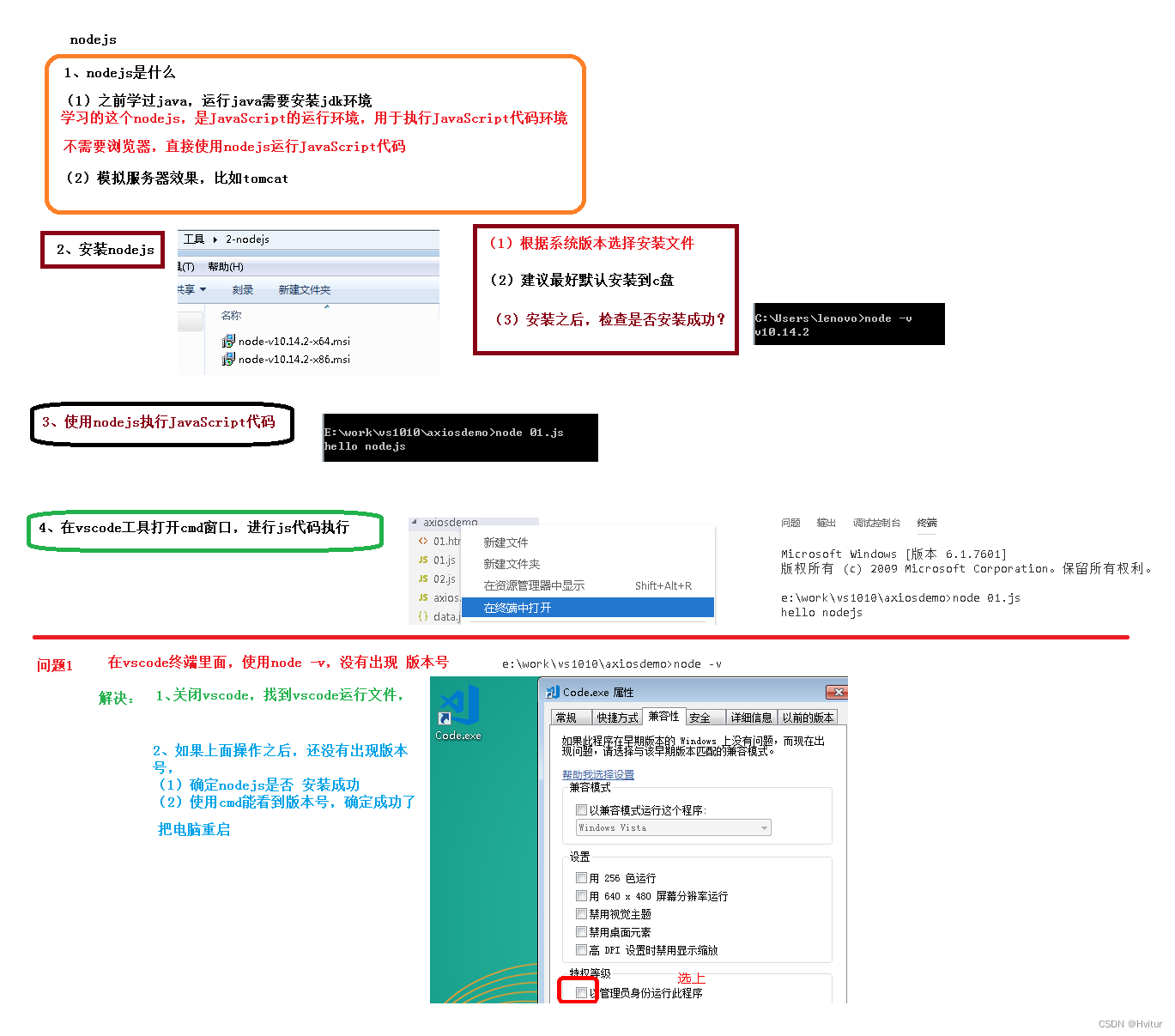
【谷粒学院】vue、axios、element-ui、node.js(44~58)
44.前端技术-vue入门 🧨Vue.js 是什么 Vue (读音 /vjuː/,类似于 view) 是一套用于构建用户界面的渐进式框架。 Vue 的核心库只关注视图层,不仅易于上手,还便于与第三方库或既有项目整合。另一方面,当与现代化的工具…...

【一些回忆】2022.02.26-2023.02.26 一个普通男孩的365天
💃🏼 本人简介:男 👶🏼 年龄:18 🤞 作者:那就叫我亮亮叭 📕 专栏:一些回忆 为什么选择在这个时间节点回忆一下呢? 一是因为今天距离2023高考仅剩1…...
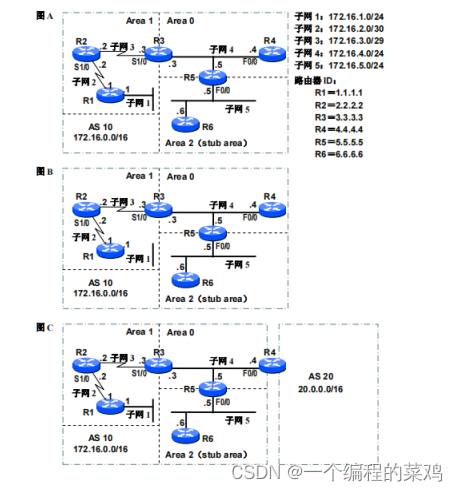
OSPF的多区域特性 (电子科技大学TCP/IP实验三)
一.实验目的 1、掌握OSPF 协议中区域的类型、特征和作用 2、掌握OSPF 路由器的类型、特征和作用 3、掌握OSPF LSA 分组的类型、特征和作用 4、理解OSPF 区域类型、路由器类型和OSPF LSA 分组类型间的相互关系 二.预备知识 1、静态路由选择和动态路…...
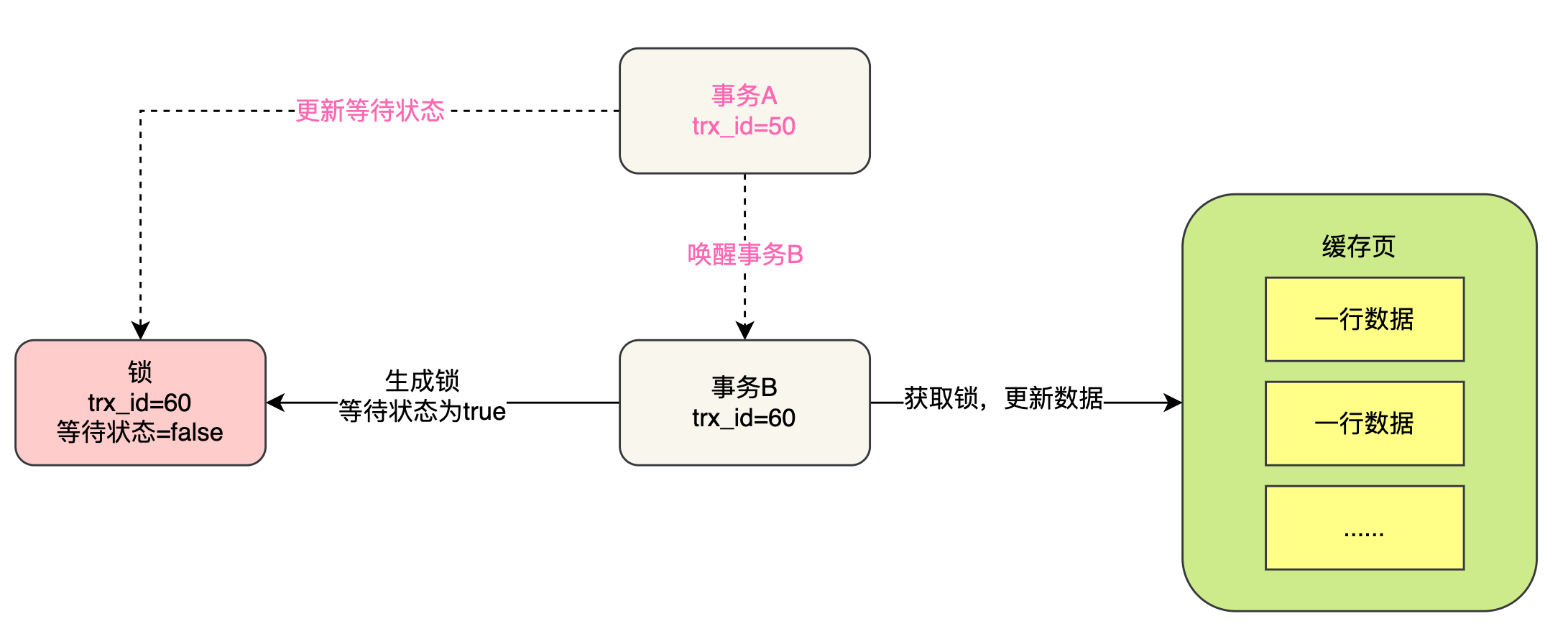
(四十四)多个事务更新同一行数据时,是如何加锁避免脏写的?
之前我们已经用很多篇幅给大家讲解了多个事务并发运行的时候,如果同时要读写一批数据,此时读和写时间的关系是如何协调的,毕竟要是你不协调好的话,可能就会有脏读、不可重复读、幻读等一系列的问题。 简单来说,脏读、…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

PCA笔记
✅ 问题本质:为什么让矩阵 TT 的行列式为 1? 这个问题通常出现在我们对数据做**线性变换(旋转/缩放)**的时候,比如在 PCA 中把数据从原始坐标系变换到主成分方向时。 📌 回顾一下背景 在 PCA 中ÿ…...

夏普比率(Sharpe ratio)
具有投资常识的人都明白,投资光看收益是不够的,还要看承受的风险,也就是收益风险比。 夏普比率描述的正是这个概念,即每承受一单位的总风险,会产生多少超额的报酬。 用数学公式描述就是: 其中࿱…...
