CSP-J 2023 T3 一元二次方程 解题报告
CSP-J 2023 T3 一元二次方程 解题报告
Link
前言
今年 C S P CSP CSP的原题, 回家 1 h 1h 1h内写 A C AC AC, 但是考场上没有写出来 , 原因是脑子太不好了, 竟然调了两个小时没有调出来. 一等奖悬那…
正题
看完题目,第一眼就是大模拟, 并且 C C F CCF CCF绝对不会让你好受,所以出了一个如此刁钻的题目, 并且要考虑到非常多的情况, 代码非常长…
最重要的一点: Δ \Delta Δ
Δ \Delta Δ是此题中最重要的分情况讨论的地方. 根据初三 22 22 22章的所学知识 ,可知分三种情况:
1. Δ < 0 \Delta < 0 Δ<0
不用说了
直接输出NO
2. Δ = 0 \Delta = 0 Δ=0
同样的, 只有一种情况, 答案为 − b 2 a - \dfrac{b}{2a} −2ab,但是, 需要严谨的判断.
if(delta == 0) {if(b == 0) {cout << 0;}else if(a * b > 0) {a = abs(a);b = abs(b);cout << "-";if(b % (2 * a) == 0) {cout << b / 2 / a;}else {cout << b / __gcd(2 * a, b) << "/" << (2 * a) / __gcd(2 * a, b);}}else {a = abs(a);b = abs(b);if(b % (2 * a) == 0) {cout << b / 2 / a;}else {cout << b / __gcd(2 * a, b) << "/" << (2 * a) / __gcd(2 * a, b);}}
}
3. Δ > 0 \Delta > 0 Δ>0
地狱.
我是分两种情况的, 一种是 a > 0 a > 0 a>0, 一种是 a < 0 a < 0 a<0. 这样可以分辨出是 + Δ + \sqrt{\Delta } +Δ 还是 − Δ -\sqrt{\Delta } −Δ
如若 a < 0 a < 0 a<0, 则可知答案为:
b + Δ − 2 a \dfrac{b + \sqrt{\Delta}}{-2a} −2ab+Δ
如若 a > 0 a > 0 a>0, 则可知答案为:
Δ − b 2 a \dfrac{\sqrt{\Delta} - b}{2a} 2aΔ−b
- 在这里有一个技巧, 就是不论怎样, 输出时, Δ \sqrt{\Delta} Δ永远是正的(符号为
+)
可以分两种情况:
1.第一种: 不需要写sqrt, 也就是 Δ \Delta Δ为完全平方数时,
比较好处理, 首先需要判断 b + Δ b + \sqrt{\Delta} b+Δ是否为 0 0 0. 如果是, 则直接输出 0 0 0; 否则输出最简分数.
其中, 一定要记住如果 ( b + Δ ) % ( 2 ∗ a ) = 0 (b + \sqrt{\Delta}) \% (2 * a) = 0 (b+Δ)%(2∗a)=0, 就直接输出一个整数.还要注意判断正负号.
2.第二种: 需要写sqrt, 很难.
首先, 先输出前面的内容, 也就是 − b 2 a -\dfrac{b}{2a} −2ab, 判断同上.
然后, 输出+, 代表符号.
接着, 找出三个变量, 也就是: x y Δ x 2 \dfrac{x}{y} \sqrt{\dfrac{\Delta}{x^2}} yxx2Δ中的 x , y 和 Δ x 2 x, y和\dfrac{\Delta}{x^2} x,y和x2Δ.其中, Δ x 2 \sqrt{\dfrac{\Delta}{x^2}} x2Δ为最简平方根数.
接下来是 4 4 4种情况:
x = y x = y x=y, 只有 Δ x 2 \sqrt{\dfrac{\Delta}{x^2}} x2Δ;
x % y = 0 x \% y = 0 x%y=0, 只有 x y Δ x 2 \dfrac{x}{y}\sqrt{\dfrac{\Delta}{x^2}} yxx2Δ
y % x = 0 y \% x = 0 y%x=0, 只有 Δ x 2 y \dfrac{\sqrt{\dfrac{\Delta}{x^2}}}{y} yx2Δ
其他情况, 输出 x × Δ x 2 y \dfrac{x \times \sqrt{\dfrac{\Delta}{x^2}}}{y} yx×x2Δ
完结撒花!!
C o d e : Code: Code:
- 心脏病患者请勿观看
#include <bits/stdc++.h>
using namespace std;int T, M;
int a, b, c;int pd(int x) {for(int i = sqrt(x) + 1; i >= 1; --i) {if(x % (i * i) == 0) {return i;}}
}int main() {cin >> T >> M;while(T--) {cin >> a >> b >> c;int delta;delta = b * b - 4 * a * c;if(delta < 0) {cout << "NO";}else if(delta == 0) {if(b == 0) {cout << 0;}else if(a * b > 0) {a = abs(a);b = abs(b);cout << "-";if(b % (2 * a) == 0) {cout << b / 2 / a;}else {cout << b / __gcd(2 * a, b) << "/" << (2 * a) / __gcd(2 * a, b);}}else {a = abs(a);b = abs(b);if(b % (2 * a) == 0) {cout << b / 2 / a;}else {cout << b / __gcd(2 * a, b) << "/" << (2 * a) / __gcd(2 * a, b);}}}else {if(a < 0) {int mother = - 2 * a;int x = pd(delta);int y = delta / x / x;if(b == 0) {mother = abs(mother);if(y == 1) {if(x == mother) {cout << "1";}else if(x % mother == 0) {cout << x / mother;}else {cout << x / __gcd(x, mother) << "/" << mother / __gcd(x, mother);}}else {if(x == mother) {cout << "sqrt(" << y << ")";}else if(mother % x == 0) {cout << "sqrt(" << y << ")";cout << "/" << mother / x;}else if(x % mother == 0) {cout << x / mother << "*sqrt(" << y << ")";}else {cout << x / __gcd(x, mother) << "*sqrt(" << y << ")" << "/" << mother / __gcd(x, mother);}}}else if(y == 1) { // 不需要sqrt// 说明可以合并为同一个式子int son = - b - x;if(son == 0) {cout << 0;}else if(son * mother < 0) { // 如果分子分母同号.son = abs(son);mother = abs(mother);if(son % mother == 0) {cout << son / mother;}else {cout << son / __gcd(son, mother) << "/" << mother / __gcd(son, mother);}}else { // 如果分子分母异号.son = abs(son);mother = abs(mother);cout << "-";if(son % mother == 0) {cout << son / mother;}else {cout << son / __gcd(son, mother) << "/" << mother / __gcd(son, mother);}}}else { // 需要sqrt.// 1. 先输出前面的if(b > 0) { // 不需要负号b = abs(b);mother = abs(mother);if(b % mother == 0) {cout << b / mother;}else {cout << b / __gcd(b, mother) << "/" << mother / __gcd(b, mother);}}else { // 需要负号b = abs(b);mother = abs(mother);cout << "-";if(b % mother == 0) {cout << b / mother;}else {cout << b / __gcd(b, mother) << "/" << mother / __gcd(b, mother);}}// 2. 输出sqrt部分(不管怎样都是+)cout << "+";if(x == 1) { // 不需要输出前缀.cout << "sqrt(" << y << ")";cout << "/" << - 2 * a;}else {if(x == mother) {cout << "sqrt(" << y << ")";}else if(x % mother == 0) {cout << x / mother << "*sqrt(" << y << ")";}else if(mother % x == 0) {cout << "sqrt(" << y << ")";cout << "/" << mother / x;}else {cout << x / __gcd(x, mother);cout << "*sqrt(" << y << ")";cout << "/" << mother / __gcd(x, mother);}}}}else {int mother = 2 * a;int x = pd(delta);int y = delta / x / x;if(b == 0) {mother = abs(mother);if(y == 1) {if(x == mother) {cout << "1";}else if(x % mother == 0) {cout << x / mother;}else {cout << x / __gcd(x, mother) << "/" << mother / __gcd(x, mother);}}else {if(x == mother) {cout << "sqrt(" << y << ")";}else if(mother % x == 0) {cout << "sqrt(" << y << ")";cout << "/" << mother / x;}else if(x % mother == 0) {cout << x / mother << "*sqrt(" << y << ")";}else {cout << x / __gcd(x, mother) << "*sqrt(" << y << ")" << "/" << mother / __gcd(x, mother);}}}else if(y == 1) { // 不需要sqrt// 说明可以合并为同一个式子int son = - b + x;if(son == 0) {cout << 0;}else if(son * mother > 0) { // 如果分子分母同号.son = abs(son);mother = abs(mother);if(son % mother == 0) {cout << son / mother;}else {cout << son / __gcd(son, mother) << "/" << mother / __gcd(son, mother);}}else { // 如果分子分母异号.son = abs(son);mother = abs(mother);cout << "-";if(son % mother == 0) {cout << son / mother;}else {cout << son / __gcd(son, mother) << "/" << mother / __gcd(son, mother);}}}else { // 需要sqrt.// 1. 先输出前面的if(b * mother < 0) { // 不需要负号b = abs(b);mother = abs(mother);if(b % mother == 0) {cout << b / mother;}else {cout << b / __gcd(b, mother) << "/" << mother / __gcd(b, mother);}}else { // 需要负号b = abs(b);mother = abs(mother);cout << "-";if(b % mother == 0) {cout << b / mother;}else {cout << b / __gcd(b, mother) << "/" << mother / __gcd(b, mother);}}// 2. 输出sqrt部分(不管怎样都是+)cout << "+";if(x == 1) { // 不需要输出前缀.cout << "sqrt(" << y << ")";cout << "/" << 2 * a;}else {mother = 2 * a;if(x == mother) {cout << "sqrt(" << y << ")";}else if(x % mother == 0) {cout << x / mother << "*sqrt(" << y << ")";}else if(mother % x == 0) {cout << "sqrt(" << y << ")";cout << "/" << mother / x;}else {cout << x / __gcd(x, mother);cout << "*sqrt(" << y << ")";cout << "/" << mother / __gcd(x, mother);}}}}}cout << endl;}return 0;
}
相关文章:

CSP-J 2023 T3 一元二次方程 解题报告
CSP-J 2023 T3 一元二次方程 解题报告 Link 前言 今年 C S P CSP CSP的原题, 回家 1 h 1h 1h内写 A C AC AC, 但是考场上没有写出来 , 原因是脑子太不好了, 竟然调了两个小时没有调出来. 一等奖悬那… 正题 看完题目,第一眼就是大模拟, 并且 C C F CCF CCF绝对不会让你好受…...
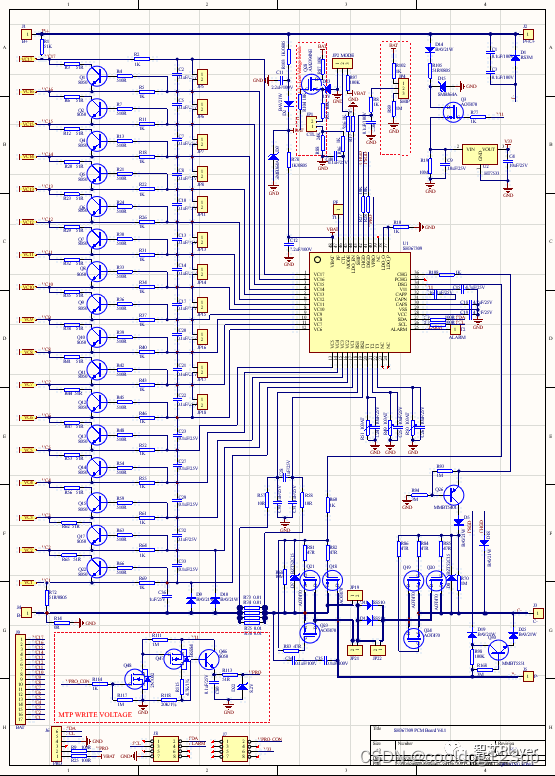
中颖单片机SH367309全套量产PCM,专用动力电池保护板开发资料
方案总体介绍 整套方案硬件部分共2块板子,包括MCU主板,采用SH79F6441-32作为主处理器。MCU主板包括2个版本。PCM动力电池保护板采用SH367309。 软件方案采用Keil51建立的工程,带蓝牙的版本,支持5~16S电池。 硬件方案--MCU主板 MC…...
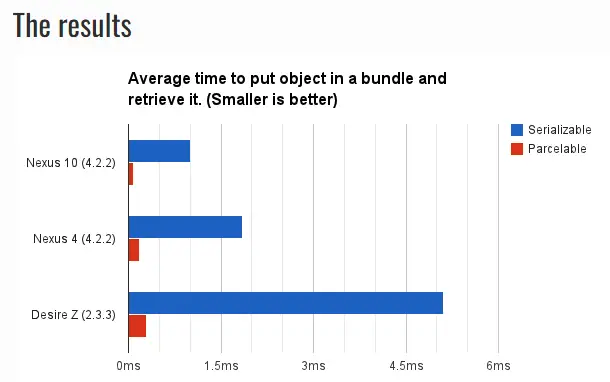
Android数据对象序列化原理与应用
序列化与反序列化 序列化是将对象转换为可以存储或传输的格式的过程。在计算机科学中,对象通常是指内存中的数据结构,如数组、列表、字典等。通过序列化,可以将这些对象转换为字节流或文本格式,以便在不同的系统之间进行传输或存…...

Linux cp命令:复制文件和目录
cp 命令,主要用来复制文件和目录,同时借助某些选项,还可以实现复制整个目录,以及比对两文件的新旧而予以升级等功能。 cp 命令的基本格式如下: [rootlocalhost ~]# cp [选项] 源文件 目标文件 选项: -a&…...

SpringBoot 接收不到 post 请求数据与接收 post 请求数据
文章归档:https://www.yuque.com/u27599042/coding_star/xwrknb7qyhqgdt10 SpringBoot 接收不到 post 请求数据 接收 post 请求数据,控制器方法参数需要使用 RequestParam 注解修饰 public BaseResponseResult<Object> getMailCode(RequestParam…...
vue3学习(十四)--- vue3中css新特性
文章目录 样式穿透:deep()scoped的原理 插槽选择器:slotted()全局选择器:global()动态绑定CSScss module 样式穿透:deep() 主要是用于修改很多vue常用的组件库(element, vant, AntDesigin),虽然配好了样式但是还是需要更改其他的样式就需要用…...

Python爬虫基础之Requests详解
目录 1. 简介2. 安装3. 发送请求4. 处理响应5. IP代理6. Cookie登录参考文献 原文地址:https://program-park.top/2023/10/27/reptile_4/ 本文章中所有内容仅供学习交流使用,不用于其他任何目的,严禁用于商业用途和非法用途,否则由…...

C++求根节点到叶子节点数字之和
文章目录 题目链接题目描述解题思路代码复杂度分析 题目链接 LCR 049. 求根节点到叶节点数字之和 - 力扣(LeetCode) 题目描述 给定一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表…...
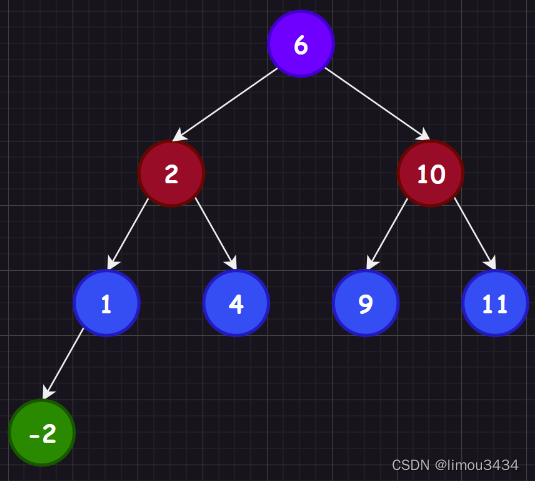
C++搜索二叉树
本章主要是二叉树的进阶部分,学习搜索二叉树可以更好理解后面的map和set的特性。 1.二叉搜索树概念 二叉搜索树的递归定义为:非空左子树所有元素都小于根节点的值,非空右子树所有元素都大于根节点的值,而左右子树也是二叉搜索树…...
软件工程17-18期末试卷
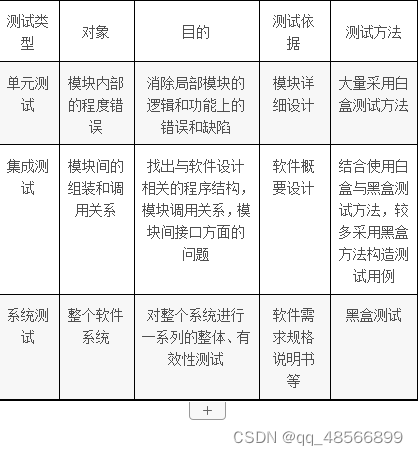
2.敏捷开发提倡一个迭代80%以上的时间都在编程,几乎没有设计阶段。敏捷方法可以说是一种无计划性和纪律性的方法。错 敏捷开发是一种软件开发方法论,它强调快速响应变化、持续交付有价值的软件、紧密合作和适应性。虽然敏捷方法鼓励迭代开发和灵活性&…...
课题学习(九)----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记
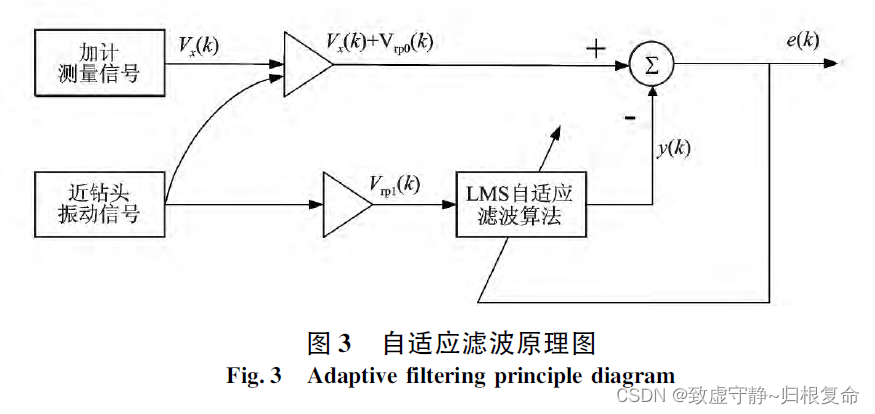
一、 引言 引言直接从原论文复制,大概看一下论文的关键点: 垂直导向钻井工具在近钻头振动和工具旋转的钻井工作状态下,工具姿态参数的动态测量精度不高。为此,通过理论分析和数值仿真,提出了转速补偿的算法以消除工具旋…...

阿里云服务器—ECS快速入门
这里对标阿里云的课程,一步步学习,链接在下面,学习完考试及格即可获取阿里云开发认证和领取证书,大家可以看看这个,这里我当作笔记,记一下提升印象! 内容很长,请耐心看完࿰…...

Hive简介及核心概念
本专栏案例数据集链接: https://download.csdn.net/download/shangjg03/88478038 1.简介 Hive 是一个构建在 Hadoop 之上的数据仓库,它可以将结构化的数据文件映射成表,并提供类 SQL 查询功能,用于查询的 SQL 语句会被转化为 MapReduce 作业,然后提交到 Hadoop 上运行。 …...

CrossOver 23.6.0 虚拟机新功能介绍
CrossOver 23.6.0 Mac 此应用程序允许您运行为 Microsoft Windows 编写的程序,而无需实际安装操作系统。 CrossOver 23.6.0 Mac 包括一个 Windows 程序库,用于它可以运行的 Windows 程序。 您会发现非常流行的应用程序,例如 Microsoft Word…...
(免费领源码)Java#Springboot#mysql农产品销售管理系统47627-计算机毕业设计项目选题推荐
摘 要 随着互联网趋势的到来,各行各业都在考虑利用互联网将自己推广出去,最好方式就是建立自己的互联网系统,并对其进行维护和管理。在现实运用中,应用软件的工作规则和开发步骤,采用Java技术建设农产品销售管理系统。…...

centos更改yum源
1、更改yum源 阿里云/etc/yum.repos.d/CentOS-Base.repo 金山云/etc/yum.repos.d/cloud.repo vi /etc/yum.repos.d/cloud.repo 替换为 [base] nameCentOS-$releasever - Base mirrorlisthttp://mirrorlist.centos.org/?release$releasever&arch$basearch&repoos&…...
React-快速搭建开发环境
1.安装 说明:react-excise-01是创建的文件名 npx create-react-app react-excise-01 2. 打开文件 说明:we suggest that you begin by typing:下面即是步骤。 cd react-excise-01 npm start 3.显示...

算法随想录算法训练营第四十六天| 583. 两个字符串的删除操作 72. 编辑距离
583. 两个字符串的删除操作 题目:给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 思路:这题思路主要是求出 word1 字符串和 word2 字符串中的最长相同的子字符串&…...
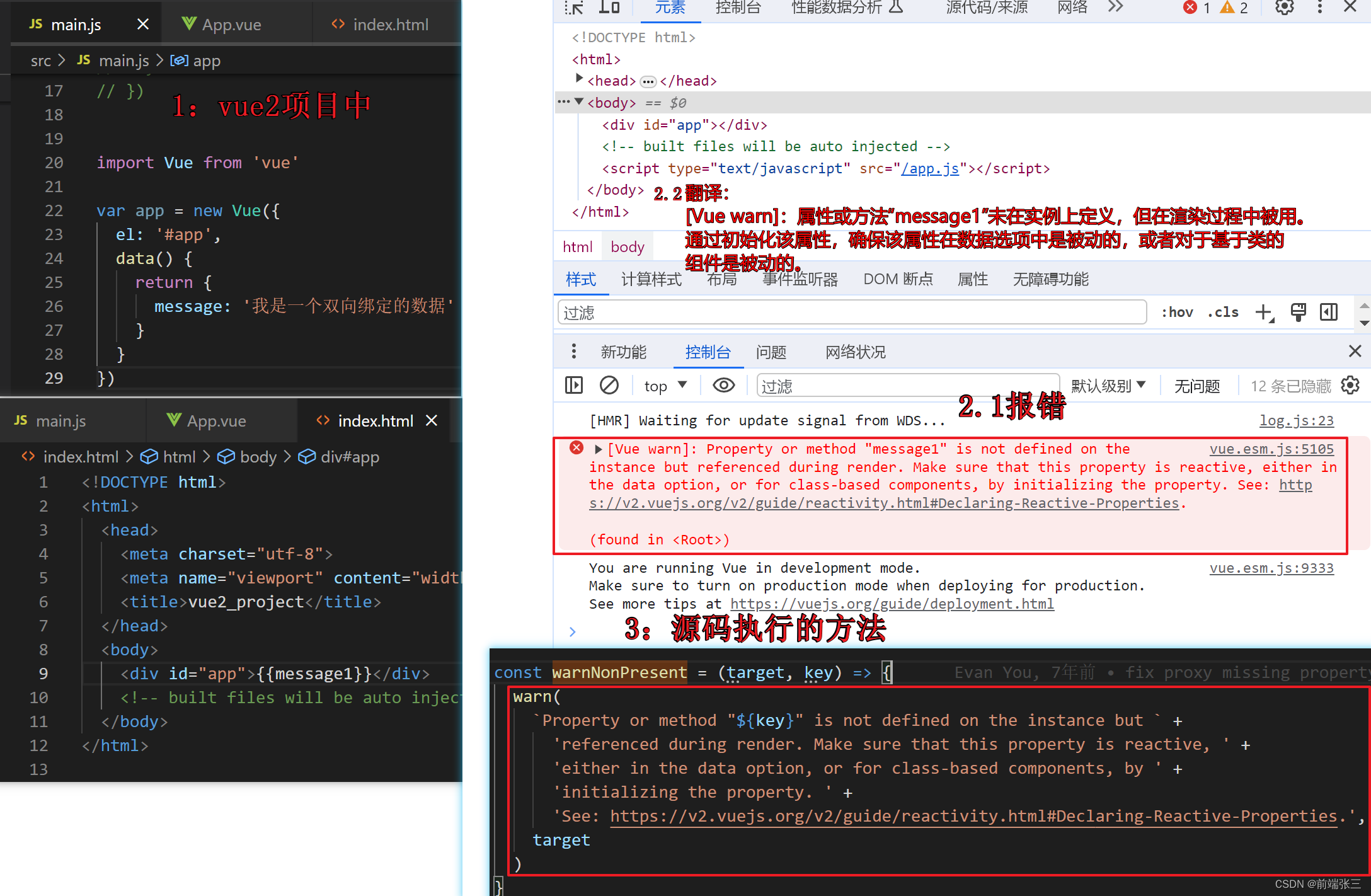
vue源码分析(五)——vue render 函数的使用
文章目录 前言一、render函数1、render函数是什么? 二、render 源码分析1.执行initRender方法2.vm._c 和 vm.$createElement 调用 createElement 方法详解(1)区别(2)代码 3、原型上的_render方法(1…...

Maven第三章:IDEA集成与常见问题
Maven第三章:IDEA集成与常见问题 前言 本章内容重点:了解如何将Maven集成到IDE(如IntelliJ IDEA或Eclipse)中,以及使用过程中遇到的常见的问题、如何解决,如何避免等,可以大大提高开发效率。 IEAD导入Maven项目 File ->Open 选择上一章创建的Maven项目 my-app查看po…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
