【通信原理】第二章|确知信号
前言
那么这里博主先安利一些干货满满的专栏了!
首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。
- 高质量博客汇总
文章目录
- 前言
- 第二章 确知信号
- 1. 确知信号的类型
- 2. 确知信号的频域性质
- 2.1 功率信号的频谱
- 2.2 周期性方波的频谱
- 2.3 能量信号的频谱密度
- 2.4 矩形脉冲的频谱密度
- 2.5 常用的傅里叶变换
- 2.6 能量信号的能量谱密度
- 2.7 功率信号的功率谱密度
- 3. 确知信号的时域性质
- 3.1 能量信号的自相关函数
- 3.2 功率信号的自相关函数
- 3.3 能量信号的互相关函数
- 3.4 功率信号的互相关函数
第二章 确知信号
1. 确知信号的类型
代表信号电压或者电流的时间波形 s ( t ) s(t) s(t)
s ( t ) s(t) \quad s(t)
信号的能量,单位焦耳。
E = ∫ − ∞ ∞ s 2 ( t ) d t E = \int_{-\infty }^{\infty} s^2(t)\mathrm{d}t E=∫−∞∞s2(t)dt
如果这个数是一个正的有限值,则信号为能量信号。与此同时,能量信号的平均功率 P = 0 P=0 P=0。
平均功率定义如下。
P = lim T → ∞ ∫ − T / 2 T / 2 s 2 ( t ) d t P = \lim_{T \to \infty } \int_{-T/2}^{T/2}s^2(t)\mathrm{d}t P=T→∞lim∫−T/2T/2s2(t)dt
两种信号。
- 能量信号,E为一个有限的正的值,但是平均功率P=0。
- 功率信号,其平均功率时等于一个有限的正值,但是能量为无穷大。
2. 确知信号的频域性质
2.1 功率信号的频谱
功率信号一般认为是周期的。(别管这么多,书上就是这样写的)
令一个周期信号 s ( t ) s(t) s(t)的周期为 T 0 T_0 T0,频谱函数可以定义成以下形式。
C n = C ( n f 0 ) = 1 T 0 ∫ − T 0 / 2 T 0 / 2 s ( t ) e − j 2 π n f 0 t d t f 0 = 1 / T 0 n 为整数 , − ∞ < n < ∞ C ( n f 0 ) 表示 C 是 n f 0 的函数,并简记为 C n C_n = C(nf_0) = \frac{1}{T_0}\int_{-T_0/2}^{T_0/2}s(t)e^{-j2\pi nf_0t}\mathrm{d}t \\ f_0 = 1/T_0 \\ n为整数, -\infty<n<\infty \\ C(nf_0)表示C是nf_0的函数,并简记为C_n Cn=C(nf0)=T01∫−T0/2T0/2s(t)e−j2πnf0tdtf0=1/T0n为整数,−∞<n<∞C(nf0)表示C是nf0的函数,并简记为Cn
傅立叶级数可以把 s ( t ) s(t) s(t)展开。
s ( t ) = ∑ n = − ∞ ∞ C n e j 2 π n t / T 0 s(t) = \sum_{n=-\infty}^{\infty} C_ne^{j2\pi nt/T_0} s(t)=n=−∞∑∞Cnej2πnt/T0
展开需要满足傅立叶级数的狄利克雷条件,一般信号是可以满足的。
当 n = 0 n=0 n=0的时候,是 s ( t ) s(t) s(t)的直流分量。
C 0 = 1 T 0 ∫ − T 0 / 2 T 0 / 2 s ( t ) d t C_{0}=\frac{1}{T_{0}} \int_{-T_{0} / 2}^{T_{0} / 2} s(t) \mathrm{d} t C0=T01∫−T0/2T0/2s(t)dt
频谱函数 C n C_n Cn是一个复数。
C n = ∣ C n ∣ e j θ n C_{n}=\left|C_{n}\right| \mathrm{e}^{\mathrm{j} \theta_{n}} Cn=∣Cn∣ejθn
对于周期性功率信号来说,频谱函数 C n C_n Cn是离散的。
重要性质。
C − n = 1 T 0 ∫ − T 0 / 2 T 0 / 2 s ( t ) e + j 2 π n f 0 t d t = [ 1 T 0 ∫ − T 0 / 2 T 0 / 2 s ( t ) e − j 2 π n f 0 t d t ] ∗ = C n ∗ C_{-n}=\frac{1}{T_{0}} \int_{-T_{0} / 2}^{T_{0} / 2} s(t) \mathrm{e}^{+\mathrm{j} 2 \pi n f_{0} t} \mathrm{~d} t=\left[\frac{1}{T_{0}} \int_{-T_{0} / 2}^{T_{0} / 2} s(t) \mathrm{e}^{-\mathrm{j} 2 \pi n f_{0} t} \mathrm{~d} t\right]^{*}=C_{n}^{*} C−n=T01∫−T0/2T0/2s(t)e+j2πnf0t dt=[T01∫−T0/2T0/2s(t)e−j2πnf0t dt]∗=Cn∗
傅立叶级数也可以展开成三角形式。
s ( t ) = C 0 + ∑ n = 1 ∞ [ a n cos ( 2 π n t / T 0 ) + b n sin ( 2 π n t / T 0 ) ] = C 0 + ∑ n = 1 ∞ [ a n 2 + b n 2 cos ( 2 π n t / T 0 + θ n ) ] 其中 θ n = − arctan ( b n / a n ) \begin{array}{l} \begin{aligned} s(t) & =C_{0}+\sum_{n=1}^{\infty}\left[a_{n} \cos \left(2 \pi n t / T_{0}\right)+b_{n} \sin \left(2 \pi n t / T_{0}\right)\right] \\ & =C_{0}+\sum_{n=1}^{\infty}\left[\sqrt{a_{n}^{2}+b_{n}^{2}} \cos \left(2 \pi n t / T_{0}+\theta_{n}\right)\right] \end{aligned}\\ 其中 \quad \theta_{n}=-\arctan \left(b_{n} / a_{n}\right) \end{array} s(t)=C0+n=1∑∞[ancos(2πnt/T0)+bnsin(2πnt/T0)]=C0+n=1∑∞[an2+bn2cos(2πnt/T0+θn)]其中θn=−arctan(bn/an)
2.2 周期性方波的频谱
C n = 1 T ∫ − τ / 2 τ / 2 V e − j 2 π n f 0 t d t = 1 T [ − V j 2 π n f 0 e − j 2 π n f 0 t ] − τ / 2 τ / 2 = V T e j 2 π n f 0 τ / 2 − e − j 2 π n f 0 τ / 2 j 2 π n f 0 = V π n f 0 T sin π n f 0 τ = V τ T S a ( n π τ T ) \begin{aligned} C_{n} & =\frac{1}{T} \int_{-\tau / 2}^{\tau / 2} V \mathrm{e}^{-\mathrm{j} 2 \pi n f_{0} t} \mathrm{~d} t=\frac{1}{T}\left[-\frac{V}{\mathrm{j} 2 \pi n f_{0}} \mathrm{e}^{-\mathrm{j} 2 \pi n f_{0} t}\right]_{-\tau / 2}^{\tau / 2} \\ & =\frac{V}{T} \frac{\mathrm{e}^{\mathrm{j} 2 \pi n f_{0} \tau / 2}-\mathrm{e}^{-\mathrm{j} 2 \pi n f_{0} \tau / 2}}{\mathrm{j} 2 \pi n f_{0}}=\frac{V}{\pi n f_{0} T} \sin \pi n f_{0} \tau= \frac{V \tau}{T} \mathrm{Sa}\left(\frac{n \pi \tau}{T}\right) \end{aligned} Cn=T1∫−τ/2τ/2Ve−j2πnf0t dt=T1[−j2πnf0Ve−j2πnf0t]−τ/2τ/2=TVj2πnf0ej2πnf0τ/2−e−j2πnf0τ/2=πnf0TVsinπnf0τ=TVτSa(Tnπτ)
记住答案,很重要。
C n = V τ T S a ( n π τ T ) C_n = \frac{V \tau}{T} \mathrm{Sa}\left(\frac{n \pi \tau}{T}\right) Cn=TVτSa(Tnπτ)
2.3 能量信号的频谱密度
注意叫法,功率信号的傅里叶系数 C n C_n Cn是叫做功率信号的频谱。
而,能量信号的傅里叶变换结果 S ( f ) S(f) S(f)叫做频谱密度。
S ( f ) = ∫ − ∞ ∞ s ( t ) e − j 2 π f t d t S(f)=\int_{-\infty}^{\infty} s(t) \mathrm{e}^{-\mathrm{j} 2 \pi f t} \mathrm{~d} t S(f)=∫−∞∞s(t)e−j2πft dt
S ( f ) S(f) S(f)的逆傅立叶变换就是原信号。
s ( t ) = ∫ − ∞ ∞ S ( f ) e j 2 π f t d f s(t)=\int_{-\infty}^{\infty} S(f) \mathrm{e}^{\mathrm{j} 2 \pi f t} \mathrm{~d} f s(t)=∫−∞∞S(f)ej2πft df
实能量信号的频谱密度和实功率信号的频谱有一个共同的特征,即负频谱和正频谱的模偶对称,相位奇对称。
∫ − ∞ ∞ s ( t ) e − j 2 π f t d t = [ ∫ − ∞ ∞ s ( t ) e + j 2 π f t d t ] ∗ S ( f ) = [ S ( − f ) ] ∗ \int_{-\infty}^{\infty} s(t) \mathrm{e}^{-\mathrm{j} 2 \pi f t} \mathrm{~d} t=\left[\int_{-\infty}^{\infty} s(t) \mathrm{e}^{+\mathrm{j} 2 \pi f t} \mathrm{~d} t\right]^{*} \\ S(f)=[S(-f)]^{*} ∫−∞∞s(t)e−j2πft dt=[∫−∞∞s(t)e+j2πft dt]∗S(f)=[S(−f)]∗
2.4 矩形脉冲的频谱密度
矩形脉冲的表达式为。
g τ ( t ) = { 1 ∣ t ∣ ⩽ τ / 2 0 ∣ t ∣ > τ / 2 g_{\tau}(t)=\left\{\begin{array}{ll} 1 & |t| \leqslant \tau / 2 \\ 0 & |t|>\tau / 2 \end{array}\right. gτ(t)={10∣t∣⩽τ/2∣t∣>τ/2
傅立叶变换结果为。
G τ ( f ) = τ S a ( π f τ ) G_\tau(f) = \tau \mathrm{Sa}(\pi f \tau) Gτ(f)=τSa(πfτ)
很重要,要记住。
2.5 常用的傅里叶变换
f ( t ) F ( w ) f ( t ) F ( w ) δ ( t ) 1 r e c t ( t / τ ) τ S a ( w τ / 2 ) 1 2 π δ ( w ) W 2 π S a ( W t 2 ) r e c t ( w W ) e j w 0 t 2 π δ ( w − w 0 ) c o s ( w 0 t ) π [ δ ( w − w 0 ) + δ ( w + w 0 ) ] s g n ( t ) 2 j w s i n ( w 0 t ) π j [ δ ( w − w 0 ) − δ ( w + w 0 ) ] j 1 π t s g n ( w ) e − α ∣ t ∣ 2 α α 2 + w 2 u ( t ) π δ ( w ) + 1 j w u ( t ) e − α t 1 α + j ω δ T ( t ) = ∑ n = − ∞ ∞ δ ( t − n T ) 2 π T ∑ n = − ∞ ∞ δ ( ω − n ⋅ 2 π T ) u ( t ) t e − α t 1 ( α + j ω ) 2 \begin{array}{cc|cc} \hline f(t) & F(w) & f(t) & F(w) \\ \hline \delta(t) & 1 & rect(t/\tau) & \tau Sa(w\tau/2) \\ 1 & 2\pi\delta(w) & \frac{W}{2\pi}Sa(\frac{Wt}{2}) & rect(\frac{w}{W}) \\ e^{jw_0t} & 2\pi\delta (w-w_0) & cos(w_0t) & \pi[\delta(w-w_0)+\delta(w+w_0)] \\ sgn(t) & \frac{2}{jw} & sin(w_0t) & \frac{\pi}{j}[\delta(w-w_0)-\delta(w+w_0)] \\ j\frac{1}{\pi t} & sgn(w) & e^{-\alpha |t| } & \frac{2\alpha}{\alpha ^2+w^2} \\ u(t) & \pi\delta(w)+\frac{1}{jw} & u(t) \mathrm{e}^{-\alpha t} & \frac{1}{\alpha+\mathrm{j} \omega}\\ \delta_{T}(t)=\sum_{n=-\infty}^{\infty} \delta(t-n T) & \frac{2 \pi}{T} \sum_{n=-\infty}^{\infty} \delta\left(\omega-n \cdot \frac{2 \pi}{T}\right) & u(t) t \mathrm{e}^{-\alpha t} & \frac{1}{(\alpha+\mathrm{j} \omega)^{2}} \\ \hline \end{array} f(t)δ(t)1ejw0tsgn(t)jπt1u(t)δT(t)=∑n=−∞∞δ(t−nT)F(w)12πδ(w)2πδ(w−w0)jw2sgn(w)πδ(w)+jw1T2π∑n=−∞∞δ(ω−n⋅T2π)f(t)rect(t/τ)2πWSa(2Wt)cos(w0t)sin(w0t)e−α∣t∣u(t)e−αtu(t)te−αtF(w)τSa(wτ/2)rect(Ww)π[δ(w−w0)+δ(w+w0)]jπ[δ(w−w0)−δ(w+w0)]α2+w22αα+jω1(α+jω)21
2.6 能量信号的能量谱密度
能量E。
E = ∫ − ∞ ∞ s 2 ( t ) d t E=\int_{-\infty}^{\infty} s^{2}(t) \mathrm{d} t E=∫−∞∞s2(t)dt
巴塞伐尔定理。
E = ∫ − ∞ ∞ s 2 ( t ) d t = ∫ − ∞ ∞ ∣ S ( f ) ∣ 2 d f E=\int_{-\infty}^{\infty} s^{2}(t) \mathrm{d} t=\int_{-\infty}^{\infty}|S(f)|^{2} \mathrm{~d} f E=∫−∞∞s2(t)dt=∫−∞∞∣S(f)∣2 df
能量谱密度。
G ( f ) = ∣ S ( f ) ∣ 2 ( J / H z ) G(f)=|S(f)|^{2} \quad(\mathrm{~J}/\mathrm{Hz}) G(f)=∣S(f)∣2( J/Hz)
由于信号 s ( t ) s(t) s(t)是实函数,所以 ∣ S ( f ) ∣ |S(f)| ∣S(f)∣是一个偶函数。
2.7 功率信号的功率谱密度
巴塞伐尔定理。
E = ∫ − T / 2 T / 2 s T 2 ( t ) d t = ∫ − ∞ ∞ ∣ S T ( f ) ∣ 2 d f E=\int_{-T / 2}^{T / 2} s_{T}^{2}(t) \mathrm{d} t=\int_{-\infty}^{\infty}\left|S_{T}(f)\right|^{2} \mathrm{~d} f E=∫−T/2T/2sT2(t)dt=∫−∞∞∣ST(f)∣2 df
功率谱密度。
P ( f ) = lim T → ∞ 1 T ∣ S T ( f ) ∣ 2 P(f) = \lim _{T \rightarrow \infty} \frac{1}{T}|S_{T}(f)|^{2} P(f)=T→∞limT1∣ST(f)∣2
功率用功率谱密度表示。
P = lim T → ∞ 1 T ∫ − ∞ ∞ ∣ S T ( f ) ∣ 2 d f = ∫ − ∞ ∞ P ( f ) d f P=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{-\infty}^{\infty}\left|S_{T}(f)\right|^{2} \mathrm{~d} f=\int_{-\infty}^{\infty} P(f) \mathrm{d} f P=T→∞limT1∫−∞∞∣ST(f)∣2 df=∫−∞∞P(f)df
3. 确知信号的时域性质
确知信号再时域中的性质主要有自相关函数和互相关函数。
3.1 能量信号的自相关函数
R ( τ ) = ∫ − ∞ ∞ s ( t ) s ( t + τ ) d t − ∞ < τ < ∞ R(\tau)=\int_{-\infty}^{\infty} s(t) s(t+\tau) \mathrm{d} t \quad-\infty<\tau<\infty R(τ)=∫−∞∞s(t)s(t+τ)dt−∞<τ<∞
自相关函数反映了一个信号延迟 τ \tau τ后的同一信号间的相关程度。自相关函数 R ( τ ) R(\tau) R(τ)和时间t无关,只和时间差 τ \tau τ有关。
当 τ = 0 \tau=0 τ=0的时候,能量信号的自相关函数 R ( 0 ) R(0) R(0)等于信号的能量。
R ( 0 ) = E 前提是能量信号 R(0) = E \quad 前提是能量信号 R(0)=E前提是能量信号
此外, R ( τ ) R(\tau) R(τ)是偶函数。
自相关函数和能量谱密度的关系。
能量谱密度的逆傅立叶变换就是能量信号的自相关函数。
R ( τ ) = ∫ − ∞ ∞ ∣ S ( f ) ∣ 2 e j 2 π f τ d f R(\tau)=\int_{-\infty}^{\infty}|S(f)|^{2} \mathrm{e}^{\mathrm{j} 2 \pi f \tau} \mathrm{d} f R(τ)=∫−∞∞∣S(f)∣2ej2πfτdf
R ( τ ) R(\tau) R(τ)和 ∣ S ( f ) ∣ 2 |S(f)|^2 ∣S(f)∣2构成一对傅立叶变换。
3.2 功率信号的自相关函数
功率信号自相关函数的定义。
R ( τ ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 s ( t ) s ( t + τ ) d t − ∞ < τ < ∞ R(\tau)=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{-T / 2}^{T / 2} s(t) s(t+\tau) \mathrm{d} t \quad-\infty<\tau<\infty R(τ)=T→∞limT1∫−T/2T/2s(t)s(t+τ)dt−∞<τ<∞
由定义可以看出, τ = 0 \tau=0 τ=0的时候,功率信号的自相关函数 R ( 0 ) R(0) R(0)等于信号的平均功率。
R ( 0 ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 s 2 ( t ) d t = P R(0)=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{-T / 2}^{T / 2} s^{2}(t) \mathrm{d} t=P R(0)=T→∞limT1∫−T/2T/2s2(t)dt=P
功率信号的自相关函数也是偶函数。
对于周期性的功率信号,自相关函数的定义可以改写为。
R ( τ ) = 1 T 0 ∫ − T 0 / 2 T 0 / 2 s ( t ) s ( t + τ ) d t − ∞ < τ < ∞ R(\tau)=\frac{1}{T_{0}} \int_{-T_{0} / 2}^{T_{0} / 2} s(t) s(t+\tau) \mathrm{d} t \quad-\infty<\tau<\infty R(τ)=T01∫−T0/2T0/2s(t)s(t+τ)dt−∞<τ<∞
功率信号的自相关函数的傅立叶变换就是功率谱密度。
P ( f ) = ∫ − ∞ ∞ R ( τ ) e − j 2 π f τ d τ P(f)=\int_{-\infty}^{\infty} R(\tau) \mathrm{e}^{-\mathrm{j} 2 \pi f \tau} \mathrm{d} \tau P(f)=∫−∞∞R(τ)e−j2πfτdτ
3.3 能量信号的互相关函数
两个能量信号 s 1 ( t ) s_1(t) s1(t)和 s 2 ( t ) s_2(t) s2(t)的互相关函数定义如下。
R 12 ( τ ) = ∫ − ∞ ∞ s 1 ( t ) s 2 ( t + τ ) d t − ∞ < τ < ∞ R_{12}(\tau)=\int_{-\infty}^{\infty} s_{1}(t) s_{2}(t+\tau) \mathrm{d} t \quad-\infty<\tau<\infty R12(τ)=∫−∞∞s1(t)s2(t+τ)dt−∞<τ<∞
顺序很重要。
R 21 ( τ ) = R 12 ( − τ ) R_{21}(\tau) = R_{12}(-\tau) R21(τ)=R12(−τ)
互相关函数和能量谱密度的关系。
互能量谱密度定义。
S 12 ( f ) = S 1 ∗ ( f ) S 2 ( f ) S_{12}(f)=S_{1}^{*}(f) S_{2}(f) S12(f)=S1∗(f)S2(f)
所以互相关函数和互能量谱密度也是一对傅立叶变换。
S 12 ( f ) = ∫ − ∞ ∞ R 12 ( τ ) e − j 2 π / τ d τ S_{12}(f)=\int_{-\infty}^{\infty} R_{12}(\tau) \mathrm{e}^{-\mathrm{j} 2 \pi / \tau} \mathrm{d} \tau S12(f)=∫−∞∞R12(τ)e−j2π/τdτ
3.4 功率信号的互相关函数
两个功率信号的互相关函数定义为。
R 12 ( τ ) = lim T → ∞ 1 T ∫ − T / 2 T / 2 s 1 ( t ) s 2 ( t + τ ) d t R_{12}(\tau)=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{-T / 2}^{T / 2} s_{1}(t) s_{2}(t+\tau) \mathrm{d} t R12(τ)=T→∞limT1∫−T/2T/2s1(t)s2(t+τ)dt
如果两个功率信号的周期相同,则其互相关函数的定义可以写成。
R 12 ( τ ) = 1 T ∫ − T / 2 T / 2 s 1 ( t ) s 2 ( t + τ ) d t − ∞ < τ < ∞ R_{12}(\tau)=\frac{1}{T} \int_{-T / 2}^{T / 2} s_{1}(t) s_{2}(t+\tau) \mathrm{d} t \quad-\infty<\tau<\infty R12(τ)=T1∫−T/2T/2s1(t)s2(t+τ)dt−∞<τ<∞
互功率谱定义。
C 12 = ( C n ) 1 ∗ ( C n ) 2 C_{12}=\left(C_{n}\right)_{1}^{*}\left(C_{n}\right)_{2} C12=(Cn)1∗(Cn)2
周期性功率信号的互功率谱 C 12 C_{12} C12是其互相关函数 R 12 ( τ ) R_{12}(\tau) R12(τ)的傅立叶级数的系数。
相关文章:

【通信原理】第二章|确知信号
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 文章目录 前言 第二章 确知信号1. 确知…...
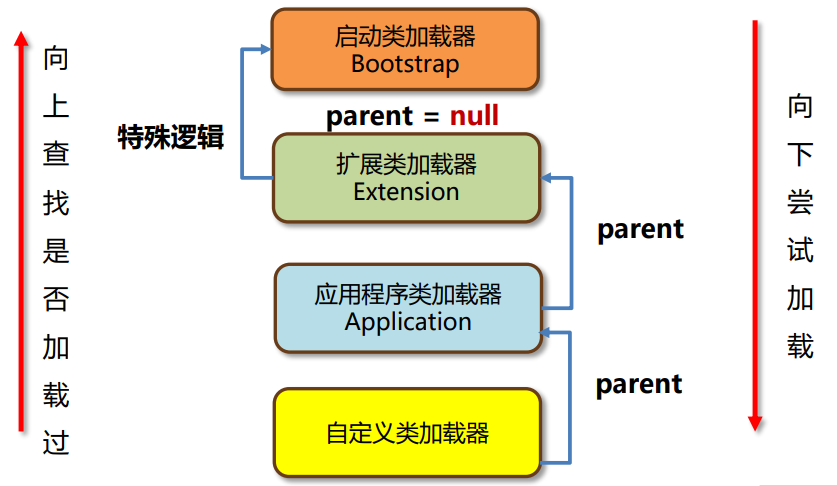
【JVM】类加载器
【JVM】类加载器 文章目录 【JVM】类加载器0. 类加载器概述1. 类加载器的分类1.1 启动类加载器1.2 Java中的默认类加载器1.2.1 扩展类加载器1.2.2 应用程序类加载器 2. 双亲委派机制2.1 类的双亲委派机制是什么?2.2 打破双亲委派机制2.2.1 自定义类加载器2.2.2 线程…...
利用Excel支持JUnit参数化测试
在JUnit里面,可以使用CsvFileSource读取csv文件进行参数化测试,可是CSV文件不支持格式,编辑颇为麻烦,尤其是多次编辑,因此自然想到是否可以使用Excel文件,可以有各种格式,支持各类数据。 最新开…...
第三章 SysML入门|系统建模语言SysML实用指南学习
仅供个人学习记录 UML与SysML的联系 可以稍微参考UML与SysML的联系 UML(统一建模语言)和SysML(系统建模语言)是两种与建模相关的语言,它们之间存在联系和区别。 SysML的图分类如下图所示。 SysML 图概述 这里只…...

敏捷开发框架Scrum-概述
如果你是一个程序员,可能会觉得这是个程序开发框架。Scrum是一个敏捷开发框架。我们可以把Scrum理解成一个团队一次完成一小部分工作的方式。这种方式通过不断的实验和反馈循环来学习和改进。Scrum可以帮助团队以协作的方式逐步交付价值。 Scrum框架由一个Scrum团队…...

Hafnium启动过程分析
安全之安全(security)博客目录导读 目录 一、在安全世界中加载Hafnium和安全分区 二、通过TF-A启动 1、SP manifests 2、安全分区包 3、描述安全分区...
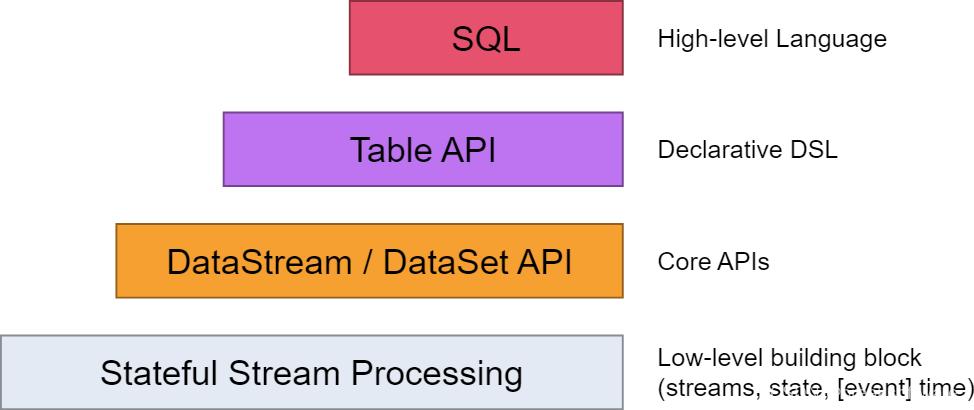
0基础学习PyFlink——使用Table API实现SQL功能
大纲 Souceschemadescriptor Sinkschemadescriptor Execute完整代码参考资料 《0基础学习PyFlink——使用PyFlink的Sink将结果输出到Mysql》一文中,我们讲到如何通过定义Souce、Sink和Execute三个SQL,来实现数据读取、清洗、计算和入库。 如下图所示SQL是最高层级的…...
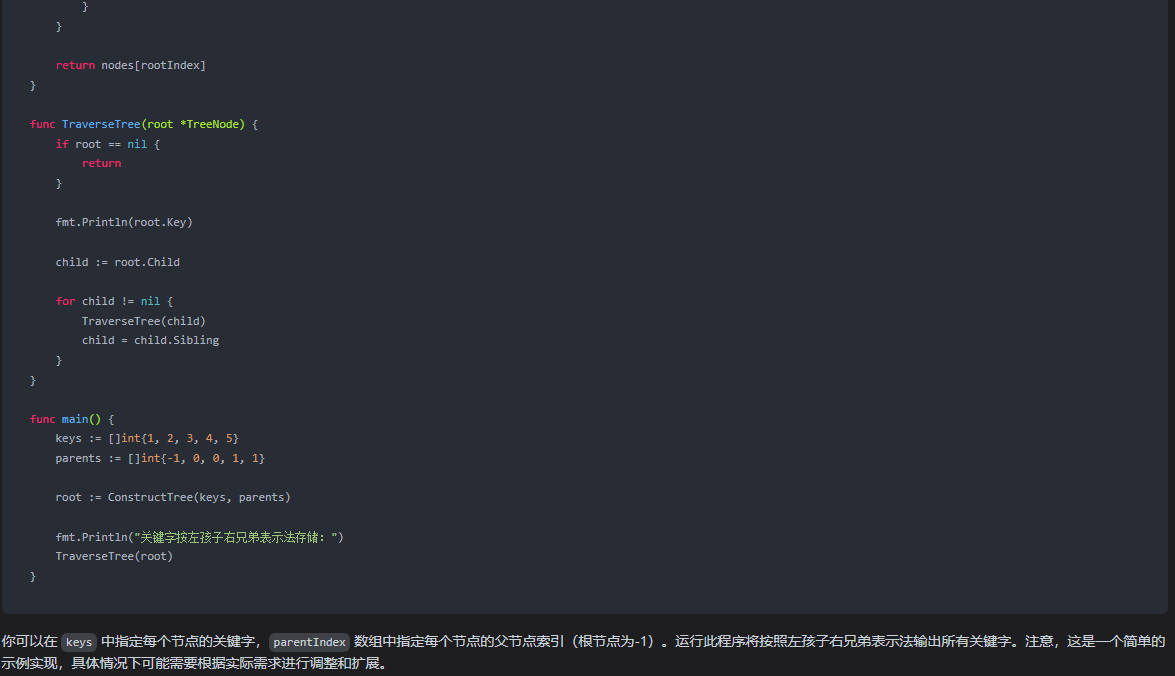
文心一言 VS 讯飞星火 VS chatgpt (123)-- 算法导论10.4 4题
四、用go语言,对于一个含 n个结点的任意有根树,写出一个 O(n)时间的过程,输出其所有关键字该树以左孩子右兄弟表示法存储。 文心一言: 在计算机科学中,左孩子右兄弟表示法是一种用于表示树状结构的方法,其…...
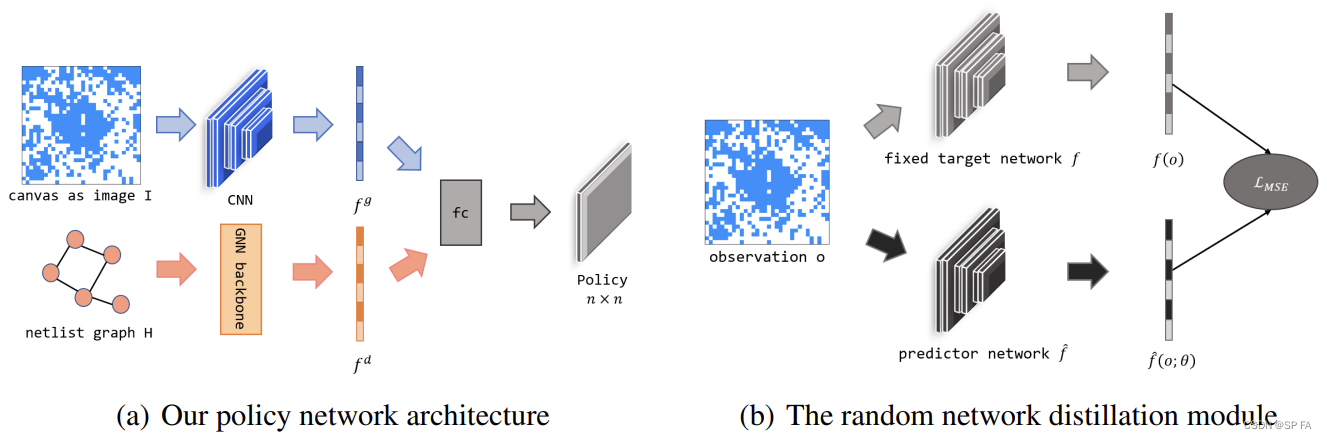
[读论文] On Joint Learning for Solving Placement and Routing in Chip Design
0. Abstract 由于 GPU 在加速计算方面的优势和对人类专家的依赖较少,机器学习已成为解决布局和布线问题的新兴工具,这是现代芯片设计流程中的两个关键步骤。它仍处于早期阶段,存在一些基本问题:可扩展性、奖励设计和端到端学习范…...

L2-1 插松枝
L2-1 插松枝 分数 25 全屏浏览题目 切换布局 作者 陈越 单位 浙江大学 人造松枝加工场的工人需要将各种尺寸的塑料松针插到松枝干上,做成大大小小的松枝。他们的工作流程(并不)是这样的: 每人手边有一只小盒子,初始…...

Android 使用ContentObserver监听SettingsProvider值的变化
1、Settings原理 Settings 设置、保存的一些值,最终是存储到 SettingsProvider 的数据库 例如: Settings.Global.putInt(getContentResolver(), "SwitchLaunch", 0); Settings.System.putInt(getContentResolver(), "SwitchLaunch&quo…...
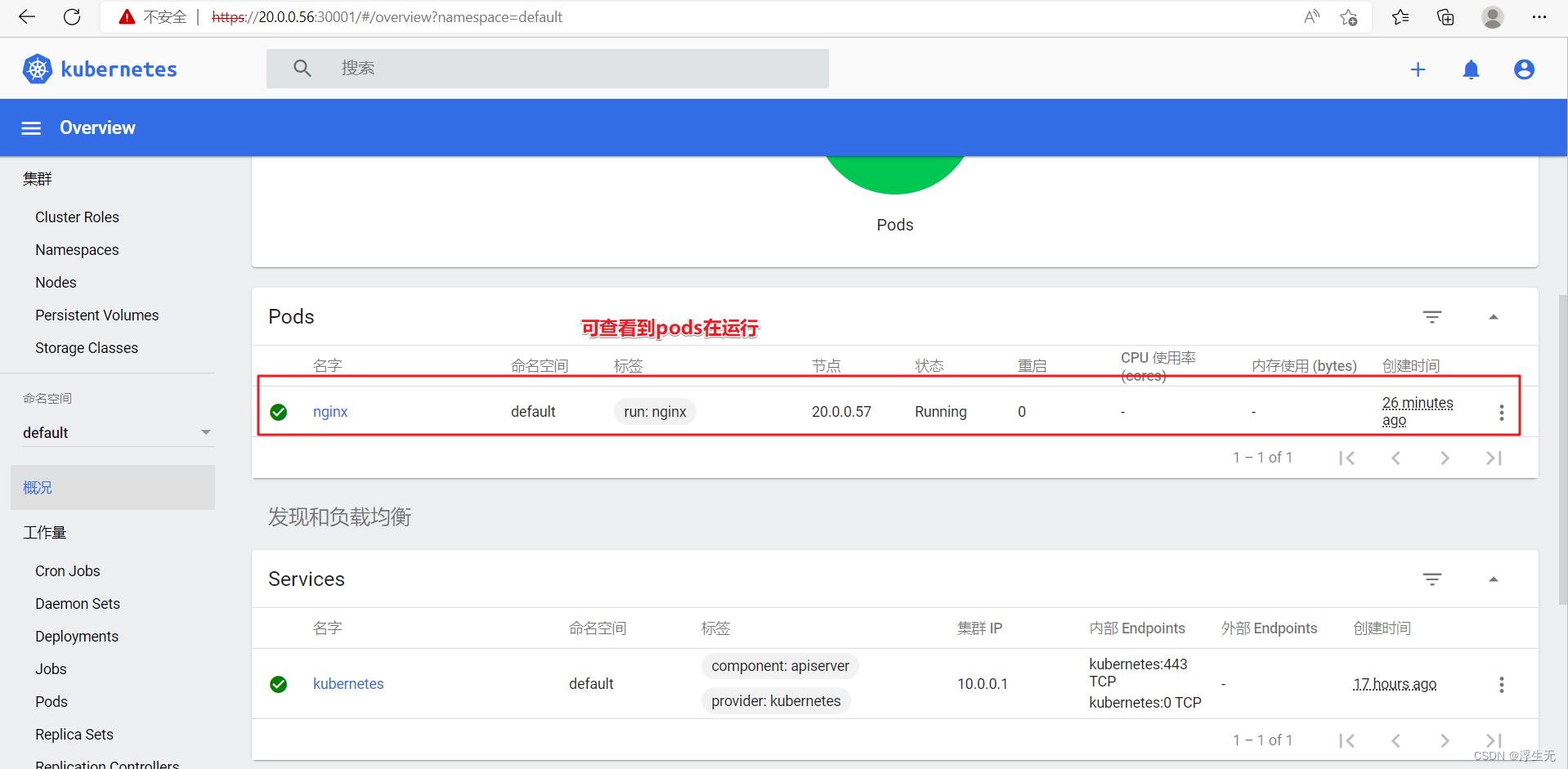
二进制安装部署k8s
概要 常见的K8S按照部署方式 minikube 是一个工具,可以在本地快速运行一个单节点微型K8S,仅用于学习,预习K8S的一些特性使用。 Kubeadmin kubeadmin也是一个工具,特工kubeadm init 和kubedm join,用于快速部署k8s…...
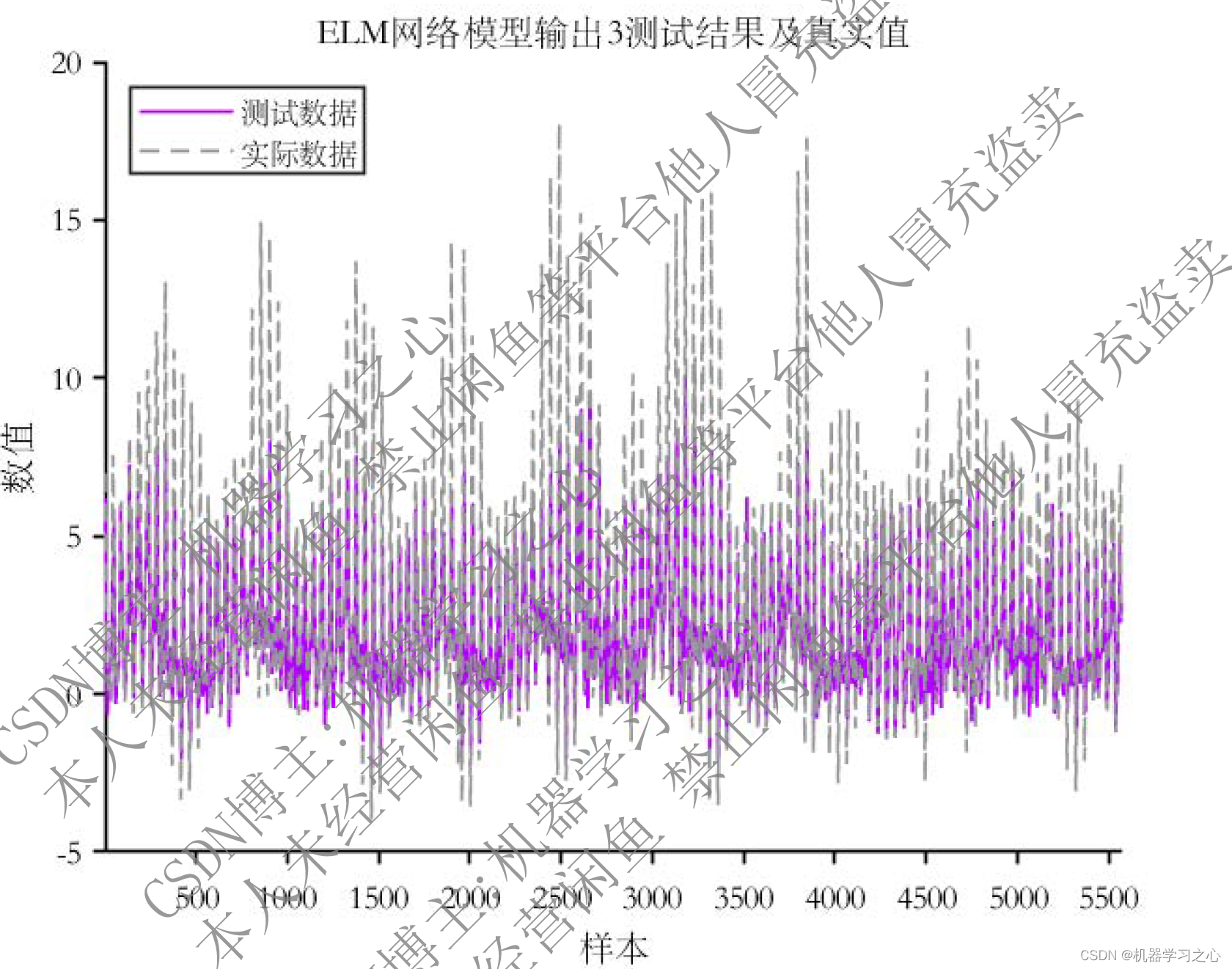
多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测
多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测 目录 多输入多输出 | Matlab实现k-means-ELM(k均值聚类结合极限学习机)多输入多输出组合预测预测效果基本描述程序设计参考资料 预测效果 基…...

ITSource 分享 第5期【校园信息墙系统】
项目介绍 本期给大家介绍一个 校园信息墙 系统,可以发布信息,表白墙,分享墙,校园二手买卖,咨询分享等墙信息。整个项目还是比较系统的,分为服务端,管理后台,用户Web端,小…...
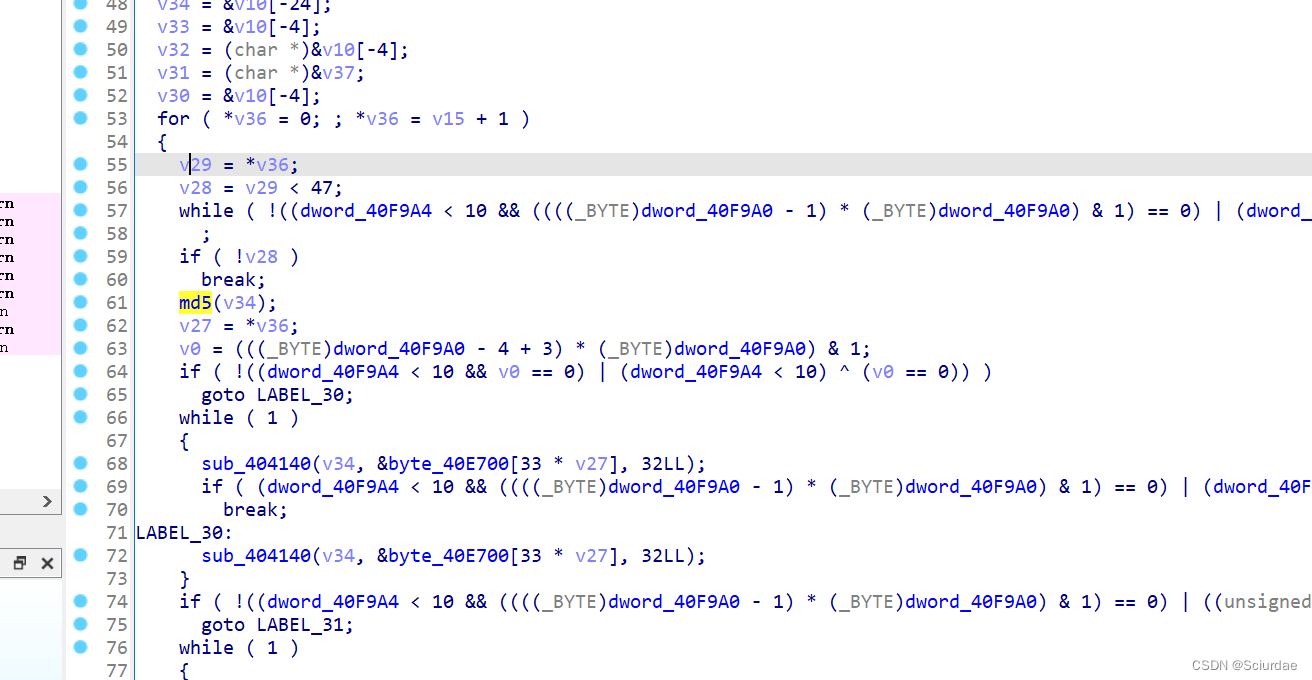
记 : CTF2023羊城杯 - Reverse 方向 Blast 题目复现and学习记录
文章目录 前言题目分析and复习过程exp 前言 羊城杯题目复现: 第一题 知识点 :DES算法 : 链接:Ez加密器 第二题 知识点 :动态调试 : 链接:CSGO 这一题的查缺补漏: 虚假控制流的去除…...

【数据结构练习题】删除有序数组中的重复项
✨博客主页:小钱编程成长记 🎈博客专栏:数据结构练习题 🎈相关博文:消失的数字 — 三种解法超详解 删除有序数组中的重复项 1.🎈题目2. 🎈解题思路3. 🎈具体代码🎇总结 1…...
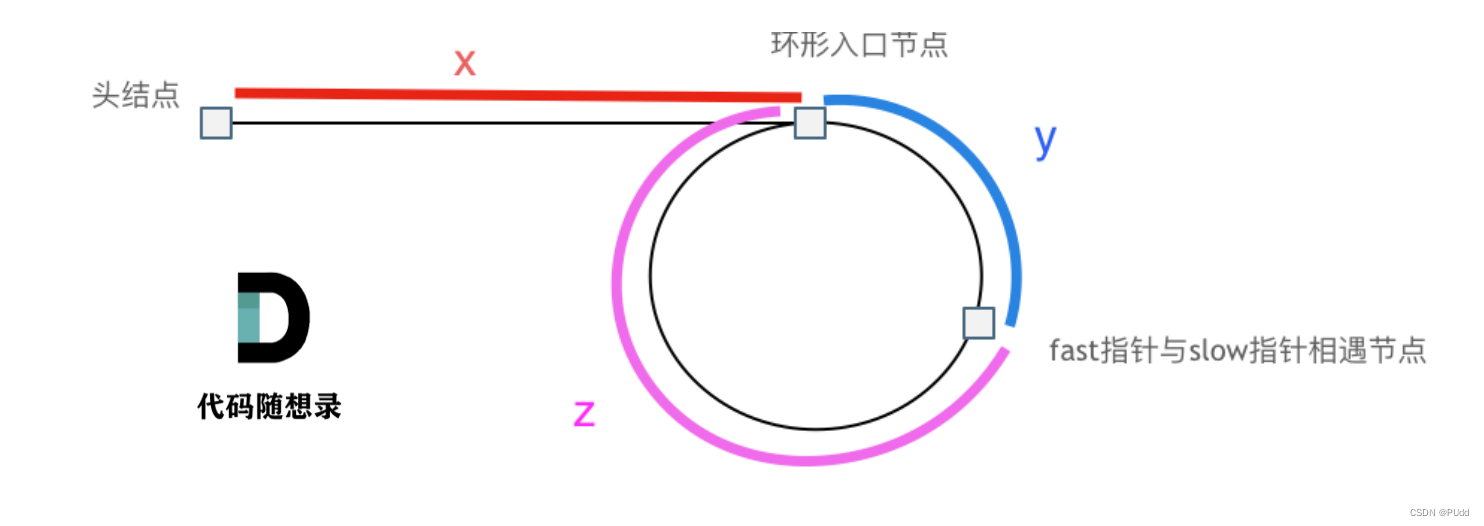
leetcode-链表
链表是一个用指针串联起来的线性结构,每个结点由数据域和指针域构成,指针域存放的是指向下一个节点的指针,最后一个节点指向NULL,第一个结点称为头节点head。 常见的链表有单链表、双向链表、循环链表。双向链表就是多了一个pre指…...
CV计算机视觉每日开源代码Paper with code速览-2023.10.27
精华置顶 墙裂推荐!小白如何1个月系统学习CV核心知识:链接 点击CV计算机视觉,关注更多CV干货 论文已打包,点击进入—>下载界面 点击加入—>CV计算机视觉交流群 1.【基础网络架构:Transformer】(Ne…...
“赋能信创,物联未来” AntDB数据库携高可用解决方案亮相2023世界数字经济大会
10月14日,在2023世界数字经济大会暨京甬信创物联网产融对接会上,AntDB数据库技术总监北陌应邀发表《AntDB国产分布式数据库创新演进与高可用解决方案》主题演讲,就AntDB数据库助力客户数智化升级的高可用信创解决方案进行了详实、真挚地分享&…...
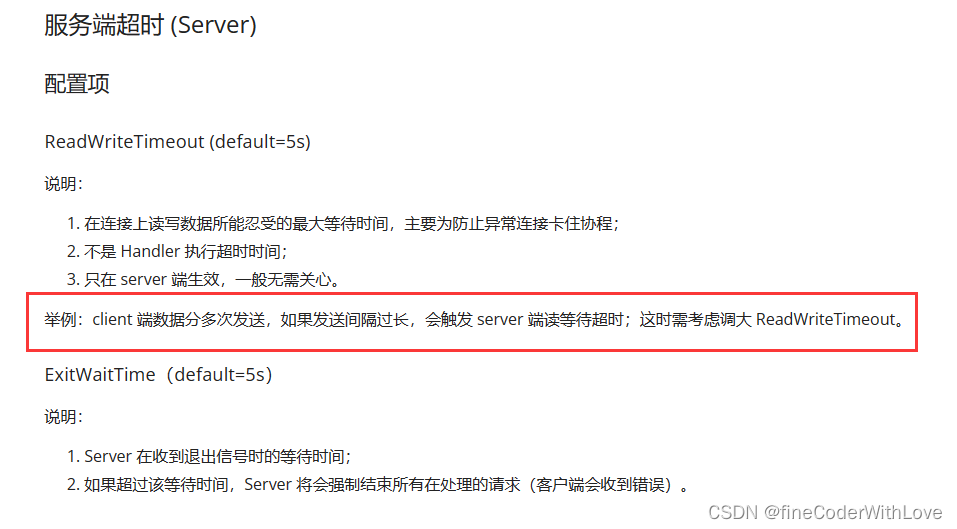
Kitex踩坑 [Error] KITEX: processing request error,i/o timeout
报错问题 2023/010/28 17:20:10.250768 default_server_handler.go:234: [Error] KITEX: processing request error, remoteService, remoteAddr127.0.0.1:65425, errordefault codec read failed: read tcp 127.0.0.1:8888->127.0.0.1:65425: i/o timeout 分析原因 Hert…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
