【面试经典150 | 栈】最小栈
文章目录
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:辅助栈
- 方法二:一个栈
- 方法三:栈中存放差值
- 其他语言
- python3
- 写在最后
Tag
【设计类】【栈】
题目来源
155. 最小栈

题目解读
本题是一个设计类的题目,设计一个最小栈类 MinStack() 实现:
MinStack():初始化堆栈对象;void push(int val):将元素val推入堆栈;void pop():删除堆栈顶部的元素;int top():获取堆栈顶部的元素;int getMin():获取堆栈中的最小元素。
解题思路
方法一:辅助栈
维护两个栈,一个栈就是常规的栈 stk1,另一个栈 stk2 用来存放已经插入栈 stk1 中数字的最小值。
注意入栈和出栈操作时两个栈都要更新。
实现代码
class MinStack {public:MinStack() {min_stk.push(INT_MAX);}void push(int val) {stk.push(val);min_stk.push(std::min(min_stk.top(), val));}void pop() {stk.pop();min_stk.pop();}int top() {return stk.top();}int getMin() {return min_stk.top();}private:std::stack<int> stk;std::stack<int> min_stk;
};/*** Your MinStack object will be instantiated and called as such:* MinStack* obj = new MinStack();* obj->push(val);* obj->pop();* int param_3 = obj->top();* int param_4 = obj->getMin();*/
复杂度分析
时间复杂度: O ( 1 ) O(1) O(1)。
空间复杂度: O ( n ) O(n) O(n), n n n 为 操作次数。
方法二:一个栈
可以只使用一个栈来同时保存当前的最小值和 val。
实现代码
class MinStack {
private:stack<pair<int, int>> stk;
public:MinStack() {stk.push(make_pair(INT_MAX, INT_MAX));}void push(int val) {stk.push({min(stk.top().first, val), val});}void pop() {stk.pop();}int top() {return stk.top().second;}int getMin() {return stk.top().first;}
};/*** Your MinStack object will be instantiated and called as such:* MinStack* obj = new MinStack();* obj->push(val);* obj->pop();* int param_3 = obj->top();* int param_4 = obj->getMin();*/
复杂度分析
时间复杂度: O ( 1 ) O(1) O(1)。
空间复杂度: O ( 1 ) O(1) O(1)。
方法三:栈中存放差值
现在我们维护一个变量 minVal,表示当前插入的变量的最小值,栈中每次入栈的是 val 与 minVal 的差值 differ。现在进行具体分析:
push(int val):如果此时栈为空,我们更新minVal = val,向栈中插入0;如果此时栈非空,首先向栈中插入diff,根据diff的值来更新minVal:- 如果
diff > 0,说明插入的val大于当前的minVal,则minVal不需要更新; - 否则表明插入的
val小于或者等于当前的minVal,则更新minVal = val。
- 如果
pop():我们需要根据diff来更新弹出栈顶元素后的minVal,具体地:- 先弹出栈顶元素
diff,并pop; - 如果
diff > 0,说明我们当时插入的val大于当时的minVal,则minVal是不需要更新的; - 否则说明当时插入的
val小于或者等于minVal,当时的minVal是插入的val,需要将minVal还原回去,即当时插入val更新minVal的过程如下,还原回去得到minVal = minVal + diff。
- 先弹出栈顶元素
d i f f = v a l − m i n V a l ; m i n V a l = v a l ; diff = val - minVal; minVal = val; diff=val−minVal;minVal=val;
top():如果diff < 0,表示minVal就是最小栈的栈顶元素,否则minVal + diff才是最小栈的栈顶元素。getMin():直接返回minVal即可。
实现代码
class MinStack {
private:stack<long long> stk;long long minVal, diff;
public:MinStack() {}void push(int val) {if (stk.empty()) {stk.push(0);minVal = val;}else {diff = val - minVal;stk.push(diff);minVal = diff > 0 ? minVal : val;}}void pop() {diff = stk.top();stk.pop();if (diff < 0) {minVal = minVal - diff;}}int top() {return stk.top() < 0 ? minVal : minVal + stk.top();}int getMin() {return minVal;}
};/*** Your MinStack object will be instantiated and called as such:* MinStack* obj = new MinStack();* obj->push(val);* obj->pop();* int param_3 = obj->top();* int param_4 = obj->getMin();*/
复杂度分析
时间复杂度: O ( 1 ) O(1) O(1)。
空间复杂度: O ( 1 ) O(1) O(1)。
其他语言
python3
以下只给出方法三的 python3 代码,该方法比较巧妙,值得好好研究。
class MinStack:def __init__(self):"""initialize your data structure here."""self.stack = []def push(self, x: int) -> None:if not self.stack:self.stack.append(0)self.min_value = xelse:diff = x-self.min_valueself.stack.append(diff)self.min_value = self.min_value if diff > 0 else xdef pop(self) -> None:if self.stack:diff = self.stack.pop()if diff < 0:self.min_value = self.min_value - diffdef top(self) -> int:return self.min_value if self.stack[-1] < 0 else self.stack[-1] + self.min_valuedef getMin(self) -> int:return self.min_value if self.stack else -1
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【面试经典150 | 栈】最小栈
文章目录 Tag题目来源题目解读解题思路方法一:辅助栈方法二:一个栈方法三:栈中存放差值 其他语言python3 写在最后 Tag 【设计类】【栈】 题目来源 155. 最小栈 题目解读 本题是一个设计类的题目,设计一个最小栈类 MinStack() …...
Linux网络基础2 -- 应用层相关
一、协议 引例:编写一个网络版的计算器 1.1 约定方案:“序列化” 和 “反序列化” 方案一:客户端发送形如“11”的字符串,再去解析其中的数字和计算字符,并且设限(如数字和运算符之间没有空格; 运算符只…...

【Python机器学习】零基础掌握SkewedChi2Sampler内核近似特征
有没有遇到这样的困扰:即使在拥有大量数据的条件下,传统的机器学习模型表现依然不佳?这时,数据预处理和特征工程成了解决问题的关键步骤。那么,有没有一种算法能够优化特征,提升模型性能呢? 假设一个在线商城希望通过用户行为(比如点击、购买等)来预测用户是否会成为…...
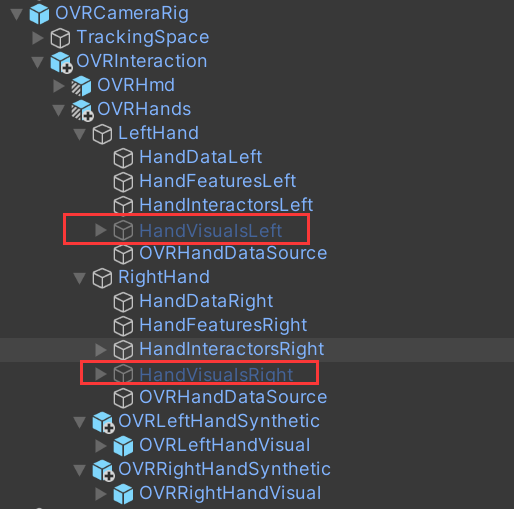
Unity Meta Quest 一体机开发(三):Oculus Integration 基本原理、概念与结构+玩家角色基本配置
文章目录 📕教程说明📕输入数据📕Oculus Integration 处理手部数据的推荐流程📕VR 中交互的基本概念📕Oculus Integration 中的交互流程📕配置一个基本的玩家物体⭐OVRCameraRig⭐OVRInteraction⭐OVRHandP…...

excel 拼接字符 单元格
需要将单元格作为字符串拼接,使用 & 符号,拼接逗号,分号,冒号,横杠等,需要用英文双引号。...
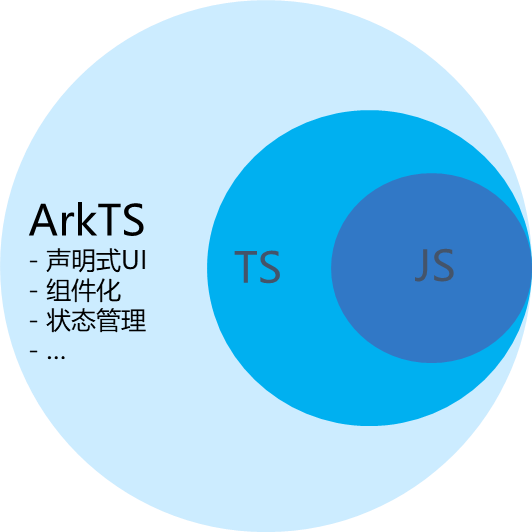
HarmonyOS 快速入门TypeScript
1.什么是TypeScript,它和JavaScript,ArkTs有什么区别 ArkTS是HarmonyOS优选的主力应用开发语言。它在TypeScript(简称TS)的基础上,匹配ArkUI框架,扩展了声明式UI、状态管理等相应的能力,让开发…...
ChatGPT扩展系列之ChatExcel
文章目录 ChatGPT扩展系列之ChatExcel对某一列的文字进行处理对数据进行排序对数据进行计算微软官方又推出Excel AI插件ChatGPT扩展系列之ChatExcel 自从ChatGPT很空出世之后,很多基于ChatGPT的应用便如雨后春笋般应用而生,这些应用的底层本质就是利用了ChatGPT对自然语言的…...

AM@微元法和定积分的应用@平面图形面积@立体体积@曲线弧长
文章目录 abstract微元法平面图形的面积极坐标上图形面积曲边扇形面积 平行截面面积为已知的立体体积旋转体的体积绕 x x x轴旋转绕 y y y轴旋转另一类型旋转体积 曲线弧长参数方程表示的曲线弧长直角坐标方程表示的曲线弧长极坐标方程表示得曲线弧长小结 abstract 微元法定积…...
SparkStreaming【实例演示】
前言 1、环境准备 启动Zookeeper和Kafka集群导入依赖: <dependency><groupId>org.apache.spark</groupId><artifactId>spark-core_2.12</artifactId><version>3.2.4</version></dependency><dependency>&l…...

提高抖音小店用户黏性和商品销量的有效策略
抖音小店是抖音平台上的电商模式,用户可以在抖音上购买各类商品。要提高用户黏性和商品销量,四川不若与众帮你整理了需要注意以下几个方面。 首先,提供优质的商品和服务。在抖音小店中,用户会通过观看商品展示视频和用户评价来选…...

提高公众意识:共同防范AI诈骗
随着人工智能技术的飞速发展,AI诈骗成为了一个不容忽视的威胁,影响到我们的社交、金融和个人隐私安全。在这个数字时代,提高公众对AI诈骗的意识至关重要,以下是一些关于如何提高公众意识以防范AI诈骗的观点: 认知AI诈…...

MES的物料管理
----物料管理的定义和作用---- 物料管理在制造执行系统(MES)中扮演着至关重要的角色。通过有效的物料管理,企业可以实现生产过程的高效性、准确性和可靠性,从而提高生产效率并降低成本。 一、物料管理的定义 物料管理是指对生产过…...
正点原子嵌入式linux驱动开发——Linux 多点电容触摸屏
随着智能手机的发展,电容触摸屏也得到了飞速的发展。相比电阻触摸屏,电容触摸屏有很多的优势,比如支持多点触控、不需要按压,只需要轻轻触摸就有反应。ALIENTEK的三款RGB LCD屏幕都支持多点电容触摸,本章就以ATK7016这…...
Git基础命令实践
文章目录 简介git的安装配置git的安装git的配置 git使用的基本流程创建版本库时光机穿梭版本回退工作区和暂存区管理修改撤销修改删除文件 远程仓库添加远程库从远程库克隆 总结 简介 本文主要记录了我在学习git操作的过程,以及如何使用GitHub。建议先参考廖雪峰的…...
微信小程序设计之页面文件pages
一、新建一个项目 首先,下载微信小程序开发工具,具体下载方式可以参考文章《微信小程序开发者工具下载》。 然后,注册小程序账号,具体注册方法,可以参考文章《微信小程序个人账号申请和配置详细教程》。 在得到了测…...
VScode 自定义主题各参数解析
参考链接: vscode自定义颜色时各个参数的作用(史上最全)vscode编辑器,自己喜欢的颜色 由于 VScode 搜索高亮是在是太不起眼了,根本看不到此时选中到哪个搜索匹配了,所以对此进行了配置,具体想增加更多可配置项可参考…...

Linux进程等待
文章目录 1. 为什么要进程等待2. 进程等待的方法waitwaitpid非阻塞轮询 1. 为什么要进程等待 子进程退出,如果父进程还未结束,没有管这个子进程,那么就可能会造成“僵尸进程”问题,进而出现内存泄漏 如果这个进程变成了“僵尸进程…...
python设计模式笔记1:创建型模式 工厂模式和抽象工厂模式
1.工厂模式 (1) 导入所需的模块( json 和 ElementTree )。 (2) 定义 JSON数据提取器类( JSONDataExtractor )。 (3) 定义 XML数据提取器类( XMLDataExtractor )。 (4) 添加工厂函数 dataextraction_factor…...

第五章 I/O管理 一、I/O设备的基本概念和分类
目录 一、什么是I/O设备 1、定义: 2、按特性分类: 3、按传输速率分类: 4、按信息交换的方式分类: 二、总结 一、什么是I/O设备 1、定义: I/O设备就是可以将数据输入到计算机,或者可以接收计算机输出…...
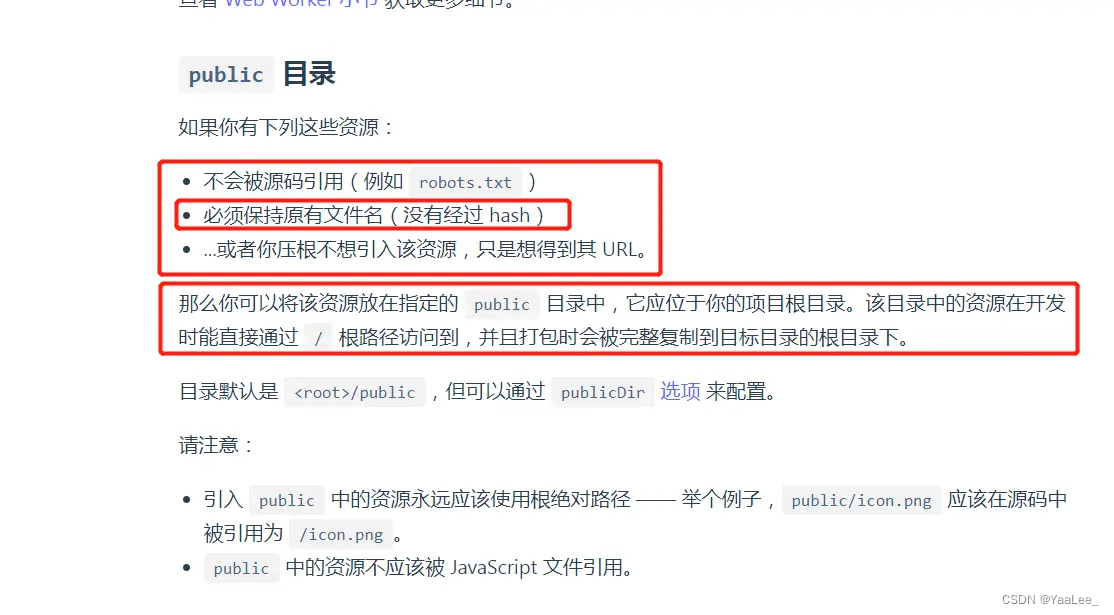
vue3动态引入图片(:src)
vite 官方默认的配置,如果资源文件在assets文件夹打包后会把图片名加上 hash值,但是直接通过 :src"imgSrc"方式引入并不会在打包的时候解析,导致开发环境可以正常引入,打包后却不能显示的问题 实际上我们不希望资源文…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
