树----数据结构
树的概念
树是一种非线性的数据结构,它是由 n (n>=1) 个有限结点组成一个具有层次关系的集合,它看起来就像一颗倒挂的树,根朝上,叶朝下。由 0 个节点构成的树,叫做空树。
树的特点:每个结点有 0 个或多个子结点。没有父节点的结点称为根结点。每个非根结点有且只有一个父结点。除了根结点以外,每个子结点可以分成多个不相交的子树。(节和结都一样)
| 专业术语 | 中文 | 描述 |
|---|---|---|
| Root | 根节点 | 一棵树的顶点 |
| Child | 孩子节点 | 一个节点含有的子树的根节点称为该节点的孩子节点 |
| Leaf | 叶子节点 | 没有孩子的节点 |
| Degree | 度 | 一个节点包含的子树的数量 |
| Edge | 边 | 一个节点与另一个节点的连接 |
| Depth | (节点)深度 | 根节点到这个节点最长路径的经过的边的数量 |
| Height | (节点)高度 | 从当前节点到叶子节点形成的最长路径中边的数量 |
| Level | (节点)层级 | 节点到根节点最长路径的边的总和 |
| Path | 路径 | 一个节点和另一个节点之间经过的边和 Node(节点)的序列 |

其中 93 是根节点,92 和 82 是 93 的孩子节点,87、82、86 是叶子节点,93 与 82 的连接线为边,不知道你有没有听过梅开二度?当然和这个关系不大,93 的度数为 2 ,因为它有两个子节点(分了两个岔),那当然 82 的度数就为 0 。

黄颜色的就是一条路径, 93 到 92 到 86。另外 86 的深度为2(到根节点的路径的边的数量),93 的深度为0,可以将根节点所在的水平当做水平面,那么你和根节点的距离就是深度了。

既然有深度,那就有高度,93 的高度为 2,可不是 1 ,因为高度取得是到叶子节点的最长路径的边数之和。
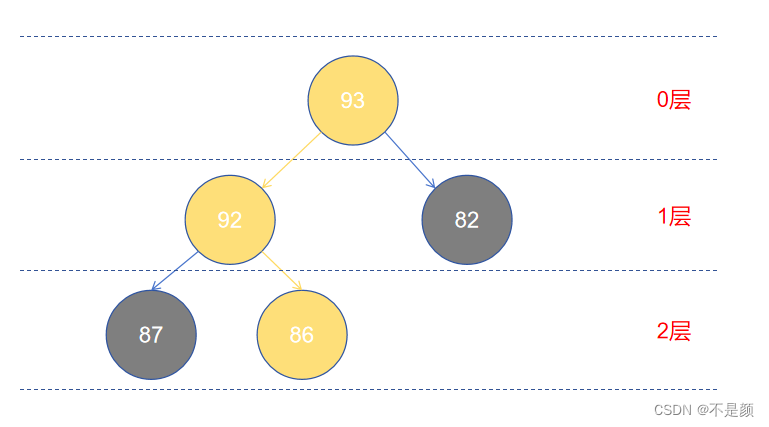
也就是节点的深度,93 的层级为 0,86 的层级为 2。
以上的概念个人认为多看看就好了,重点在下面(因为有些定义不是统一的,可能会和别人的文章有区别)。
二叉树的概念
如同线性表与栈、队列的关系,二叉树就是操作受限的树,那二叉树就是一个 一个节点最多只有两个分支的树(一个父节点最多有两个子节点),不一定一个节点一定是有两个子节点,左边的分支叫做左子树,右边的分支叫做右子树。
如图框框框住的就是子树。:

二叉树的一些性质
1、在非空二叉树中,第 i-1 层的节点总数不超过
,i >= 1
2、深度为 h-1 的二叉树最多有
- 1 个节点(h>=1),最少有 h 个节点
3、对于任意一颗二叉树,如果其叶子节点的数为 N0 ,而度数为 2 的节点的总数为 N2 ,则N0 = N2 + 1
(定义可能和书有所不同,但是意思是一样的)
对于第一点:因为第 0 层的最大节点数为 1 ,第 1 层的最大节点数为 2 ,下一层是上一层的 2 倍,以此类推。对于第二点:也能从第一点中得到深度为 h-1 的最多的节点数,最少的节点就是所有的父节点都只有一个子节点的情况。(注意是整个二叉树的节点总数)。对于第三点:二叉树最开始时只有一个根节点,叶子节点数为 1,只要根节点有两个子节点(分了两个岔路,变为了度数为 2 的节点),那叶子节点数就加 1 ,因为到最后,两个子节点的最下面一定有两个叶子节点,以此类推。
常见二叉树的分类
(1)完全二叉树-设二叉树的深度为 h,除了第 h 层外,其他层 (0~h-1) 的节点数都达到了最大个数,第 h 层有叶子节点,并且叶子节点是从左到右依次排列的,这就是完全二叉树(堆就是完全二叉树)。
如图,这就是一个完全二叉树。

那叶子节点依次排列是什么意思呢?如下图这就不是一个完全二叉树,因为叶子节点不是依次排列的,第二个和第三个叶子节点中有个空位。

(2)满二叉树-除了叶子节点外每一个节点都有左右子节点,且叶子节点处于最低层的二叉树。(也就是每层都是满的,每一层节点数达到最大),如图:
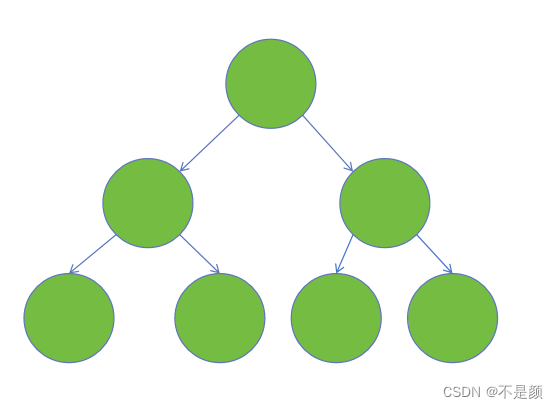
(3)平衡二叉树-又称 AVL 树,它是一颗空树(一个节点也没有)或者左右两个子树的高度差的绝对值不超过 1 ,并且左右两个子树都是平衡二叉树。
这里得注意:树的高度和节点的高度不同,因为层级是从 0 开始的,所以树的高度为层数 + 1 。

看,左子树的高度为 3 ,右子树的高度为 2 ,满足条件,别忘了子树也是平衡二叉树,和刚刚的分析一致,例如把右子树拿出来分析,如下图。

当节点的数量为 1 时,为空子树(没有孩子),高度为 1 ,故左子树的高度为 1 ,而右边啥也没有,那高度就是 0 。
(4)二叉搜索树-又称二叉查找树、二叉排序树,它是一颗空树或是满足下列性质的树:
1.若左子树不为空,则左子树上所有节点的值都小于等于它的根节点的值。
2.若右子树不为空,则右子树上所有节点的值都大于等于它的根节点的值。
3.左右子树也为二叉排序树。
二叉排序树例子:

那二叉排序树的作用是什么呢?可以用来快速地查找数据,比如有一亿个数据,要查找某个数据,理想状态只需要 27次操作就能找到,不需要遍历一亿次,是二分查找的一种特殊形式。
(5)红黑树-是每个节点都带有颜色属性(颜色为红色或者黑色)的自平衡二叉查找树,满足下列性质:
1.首先要满足二叉查找树的性质
2.节点是红色或黑色
3.根节点是黑色
4.所有的叶子节点是黑色
5.每个红色节点的子节点一定是黑色的,黑色节点的子节点无要求(从每个叶子到根的所有路径上不能有两个连续的红色节点)
6.从任一节点到其叶子节点的所有简单路径都包含相同数目的黑色节点

二叉搜索树的算法实现
引入:有一个一维数组,需要在这个数组中找到某个数字,可以遍历数组,可是这种方式效率太低。让数组有序,使用折半法(二分查找)就快得多了,可是如果需要删除或者添加数据,为了能够继续使用二分查找,就需要将数组排序,这需要移动大量的数据,显然可以使用链表存储数据,方便数据的查找和删除,可是链表却不能快速查找位置,通过比较一次排除一部分元素。
这时候二叉搜索树的应用就出现了,根据二叉搜索树的性质可以得出,它是这个场景的最佳选择(查找插入频率高)。
二叉树一般采用链式存储方式,每个节点包含两个指针域,分别指向左右孩子节点,还包含了一个数据域,存储节点的信息。如下图:

typedef int TreeDateElem;
typedef struct _BNode //二叉树
{TreeDateElem date; //元素类型struct _BNode* l; //指向左右孩子节点struct _BNode* r;
}BNode, BTree;二叉搜索树的插入
将插入的结点与根节点进行比较,如果小于等于就和左子节点进行比较,大于就和右子节点进行比较(是由二叉搜索树的性质得出的)。重复以上步骤,直到找到一个空位置,这样就可以插入了。
bool insertBtree(BNode** root, BNode* node)
{BNode *temp = NULL, *parent = NULL;if (!node){return false;}else //初始化插入节点的左右子树{node->l = NULL;node->r = NULL;}if (!*root) //根节点为空,也就是空树{*root = node;return true;}else{temp = *root;}while (temp != NULL){parent = temp; //parent 保存父节点if (node->date <= temp->date){temp = parent->l;}else{temp = parent->r;}}if (node->date < parent->date) //此时temp==NULL(找到空位置),可以进行插入{parent->l = node;}else{parent->r = node;}return true;
}二叉搜索树的删除
二叉树中节点的状态有 5 种,分别是为空、无左右子节点(叶子节点)、无左子节点、无右子节点、有左右子树(有左右子节点),对应删除操作也要分情况。
首先要比较要删除节点的值,找到节点位置。插入时已经实现过了
情况一:要删除的节点不存在左右子节点,即为叶子节点,直接删除它。

情况二:要删除的节点存在左子节点,不存在右子节点,直接将它的父节点的左孩子指针指向它的左子节点(也就是用左子节点代替它)。

情况三:要删除的节点存在右子节点,不存在左字节点,用右子节点代替删除节点(和情况二类似)。

情况四:要删除的节点存在左右子节点,则取左子树上的最大节点,或者取右子树上的最小节点来代替要删除的节点。
图为第一种情况:
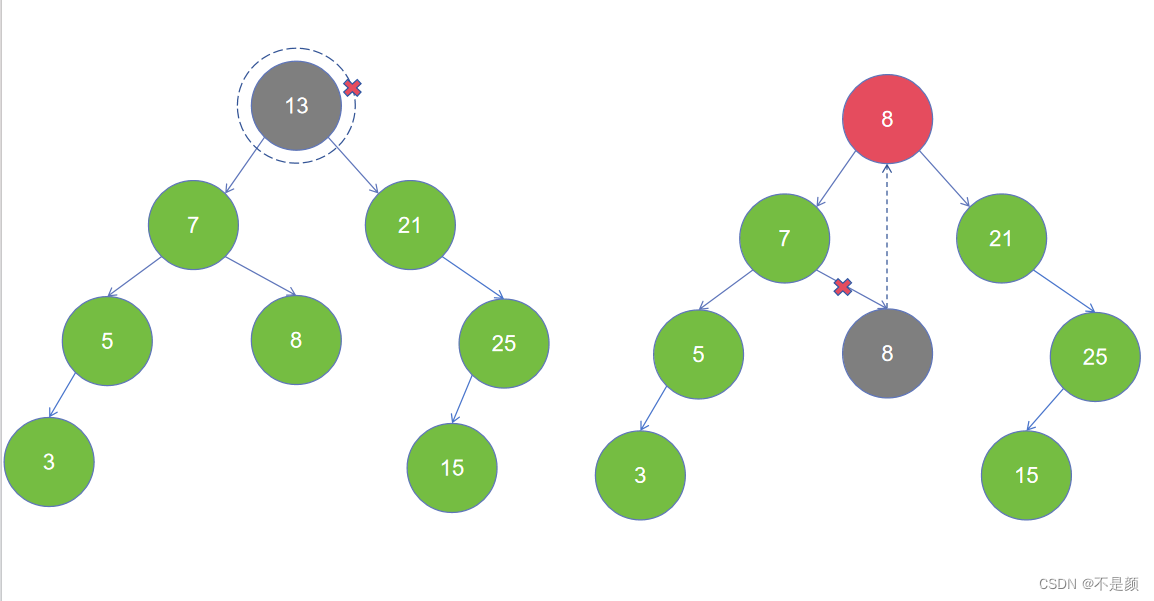
看替换后还是一颗二叉搜索树,你也可以用右子树的最小节点替换。
//二叉树的删除(采用递归的方式)
BTree* deleteBtree(BTree *root, TreeDateElem date)
{if (root == NULL) return NULL; // 没有找到节点if (date < root->date){root->l = deleteBtree(root->l, date);return root;}else if (date > root->date){root->r = deleteBtree(root->r, date);return root;}//说明找到了,因为没有继续递归//情况一:if (root->l == NULL && root->r == NULL) return NULL; //将这个节点的父节点置为空//情况二:if (root->l == NULL && root->r != NULL) return root->r; //左子节点取代//情况三:if (root->l != NULL && root->r == NULL) return root->l; //右子节点取代//情况四if (root->l != NULL && root->r != NULL) //将左子树最大的节点的值赋给这个节点,再将左子树最大的节点删除{int val = findMax(root->l);root->date = val;root->l = deleteBtree(root->l, val); return root;}//注意删除函数中并没有释放内存,可以在参数中加一个指针变量,把要删除的节点的地址返回,在主函数中释放内存return NULL; //运行不到这步,只是为了消除 不是所有的控件路径都返回值 的警告
}其中查找左子树(树)最大的节点的函数是下面这个
int findMax(BTree* root)
{assert(root != NULL);//循环实现/*while (root->r != NULL){root = root->r;}return root->date;*///递归实现if (root->r == NULL){return root->date;}return findMax(root->r);
}二叉树查找节点
BNode* queryNode(BTree* root, TreeDateElem e)
{//(递归实现)if (root == NULL || root->date==e){return root;}else if(root->date < e ){return queryNode(root->r, e); //查询右子树}else if(root->date > e ){return queryNode(root->l,e); //查询左子树}return NULL; //运行不到这步,只是为了消除 不是所有的控件路径都返回值 的警告循环实现//while (root != NULL && root->date != e)//{// if (root->date < e)// {// root = root->r;// }// else if (root->date > e)// {// root = root->l;// }//}//return root;
}二叉树的遍历
二叉树的遍历是从根节点开始,依次访问各个节点,且每个节点仅访问一次,有四种遍历方式:
前序遍历-先访问根节点,然后前序遍历左子树,再前序遍历右子树。

上图的遍历结果是:13 7 5 8 15 21 17 26
递归实现:
void visitTree2(BTree * root)
{if (root == NULL){return;}printf("-%d-", root->date);visitTree2(root->l);visitTree2(root->r);
}循环实现(非递归)申请一个栈,首先将头结点压入栈中。然后出栈,打印出栈元素的值,如果右孩子不为空,就将右孩子压入栈中,如果左孩子不为空,就将左孩子压入栈中。重复此操作直至栈为空。
void visitTree3(BTree* root)
{BNode cur;if (root == NULL){return;}Stack stack;initStack(stack);pushStack(stack, *root);while (!IsEmpty(stack)){popStack(stack, cur);printf("-%d-", cur.date);if (cur.r != NULL){pushStack(stack, *(cur.r));}if (cur.l != NULL){pushStack(stack, *(cur.l));}}destoryStack(stack);
}中序遍历-先访问根节点的左子树,再访问根节点,最后访问右子树。(这也是一个递归的过程,对于它的左子树也是先访问左子树,再访问根节点,最后访问右子树)
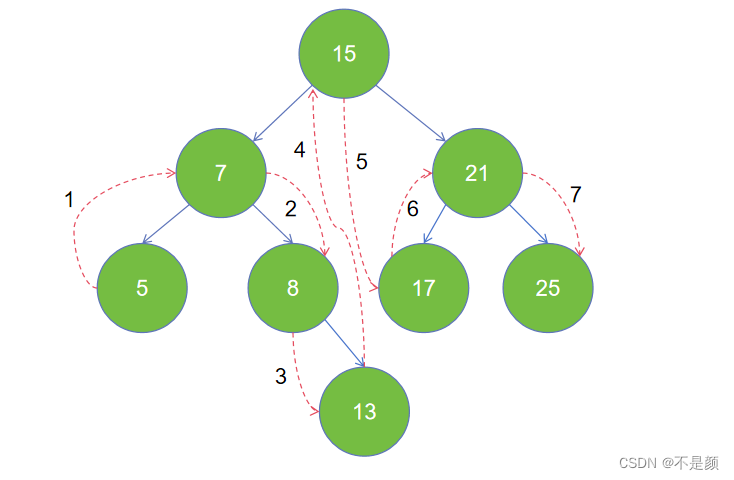
上图的遍历结果是:5 7 8 13 15 17 21 25
递归实现
void visitTree(BTree* root)
{if (root == NULL){return;}visitTree(root->l); //是不是so easy!重在理解printf("-%d-", root->date);//visitTree(root->l);visitTree(root->r);
}后序遍历-从左到右先叶子再节点的方式访问左右子树,最后是根节点。(也是一个递归的过程,先访问左子树,再访问右子树,最后访问根节点。访问左子树时,继续这个操作……)

上图的遍历结果是:5 13 8 7 17 25 21 15
后续遍历的代码就不写了。
层序遍历-从根节点从上往下逐层遍历( 0 层、1 层、2层……),对于同一层的节点,按照从左到右的顺序访问。

上图的遍历结果是:15 7 21 5 8 17 25 13
层序遍历的代码也不贴了,可以自己独立完成,可以队列实现。
最后是主函数的测试代码
其中栈的实现我也没贴出来。
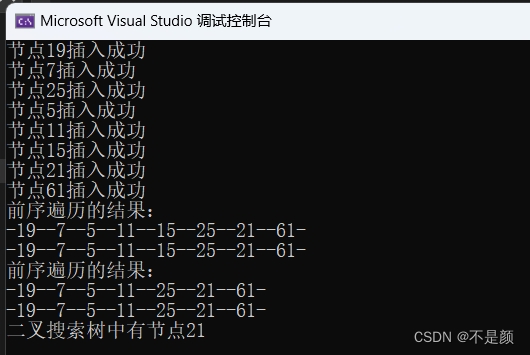
int main(void)
{int arr[] = { 19,7,25,5,11,15,21,61 };BTree *tree = NULL;BNode *node = NULL;for (int i = 0; i < sizeof(arr) / sizeof(int); i++){node = new BNode;node->date = arr[i];if (insertBtree(&tree, node)) //传递的是一级指针的地址,所以用二级指针接收{cout << "节点" << arr[i] << "插入成功" << endl;}else{cout << "节点" << arr[i] << "插入失败" << endl;}}cout << "前序遍历的结果:"<<endl;visitTree2(tree);puts("");visitTree3(tree);puts("");deleteBtree(tree, 15);cout << "前序遍历的结果:" << endl;visitTree2(tree);puts("");visitTree3(tree);puts("");BNode* temp = queryNode(tree, 21);if (temp != NULL){printf("二叉搜索树中有节点%d\n", temp->date);}else{printf("表中无此节点\n");}return 0;
}
相关文章:

树----数据结构
树的概念 树是一种非线性的数据结构,它是由 n (n>1) 个有限结点组成一个具有层次关系的集合,它看起来就像一颗倒挂的树,根朝上,叶朝下。由 0 个节点构成的树,叫做空树。 树的特点:每个结点有 0 个或多…...

GitLab定时备份
GitLab定时备份 文章目录 GitLab定时备份GitLab基础环境备份命令自动清理备份上传命令设置定时任务参考链接 GitLab基础环境 部署方式:Docker 版本:16.2.2 备份命令 Notes: 编写sh脚本时,不要使用Windows上的Notepad类似编辑…...

SQL IN 运算符
SQL IN 运算符 IN 运算符允许您在 WHERE 子句中指定多个值。 IN 运算符是多个 OR 条件的简写。 SQL IN 语法 SELECT column_name(s) FROM table_name WHERE column_name IN (value1, value2, ...); 或者 SELECT column_name(s) FROM table_name WHERE column_name IN (SELE…...

虚拟机构建单体项目及前后端分离项目
引言 在现代化办公环境中,会议是组织沟通、决策和合作的重要方式之一。为了提高会议的效率和质量,许多企业选择部署会议OA系统来实现会议管理的自动化和数字化。本博客将介绍如何部署和优化会议OA系统,并探讨前后端分离的SPA项目在此过程中的…...
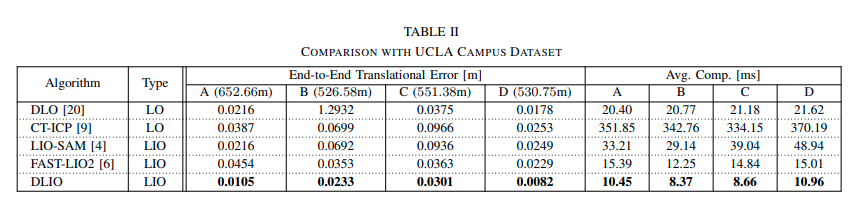
代码浅析DLIO(一)---整体框架梳理
0. 简介 我们刚刚了解过DLIO的整个流程,我们发现相比于Point-LIO而言,这个方法更适合我们去学习理解,同时官方给出的结果来看DLIO的结果明显好于现在的主流方法,当然指的一提的是,这个DLIO是必须需要六轴IMU的&#x…...
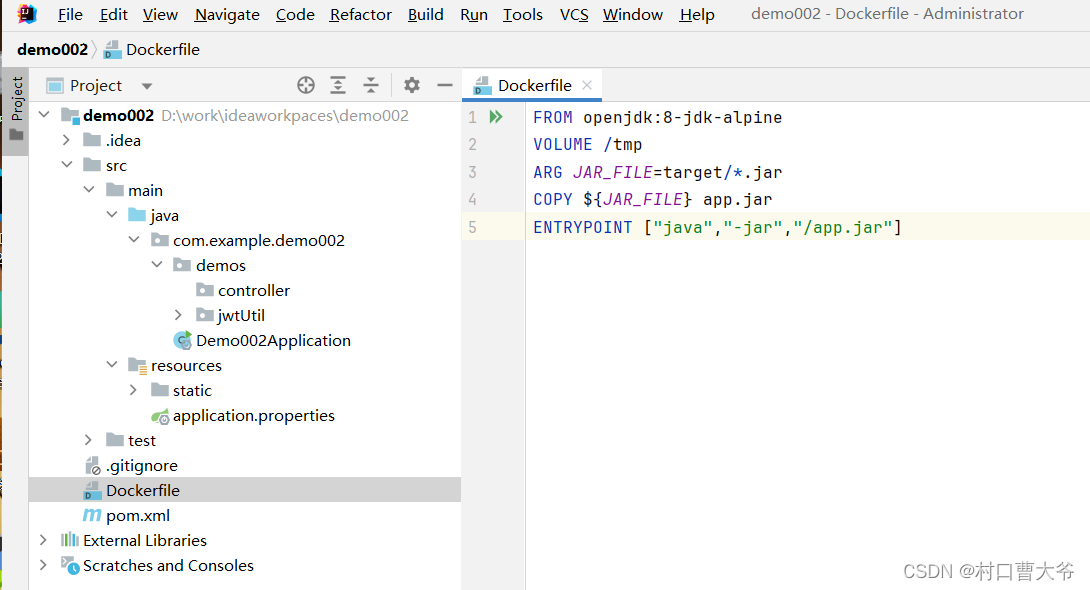
Springboot的Container Images,docker加springboot
Spring Boot应用程序可以使用Dockerfiles容器化,或者使用Cloud Native Buildpacks来创建优化的docker兼容的容器映像,您可以在任何地方运行。 1. Efficient Container Images 很容易将Spring Boot fat jar打包为docker映像。然而,像在docke…...

c 从avi 视频中提取图片
avi 视频的视频流编码必须是jpeg,或者mjpg 直接用摄像头录取的视频都是这两种格式,不能用ffmpeg转成avi的视频。 #include <stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <stdlib.…...
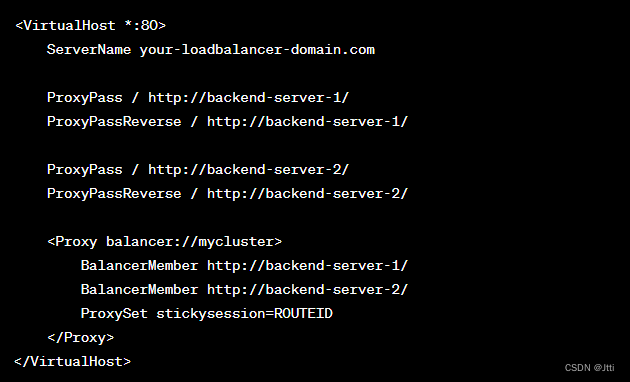
Jtti:Apache服务的反向代理及负载均衡怎么配置
配置Apache服务的反向代理和负载均衡可以帮助您分散负载并提高应用程序的可用性和性能。下面是一些通用的步骤,以配置Apache反向代理和负载均衡。 1. 安装和配置Apache: 确保您已经安装了Apache HTTP服务器。通常,Apache的配置文件位于/etc…...

82.二分查找
目录 什么是二分查找 一、左闭右闭写法[left,right] 代码演示: 二、左闭右开写法[left,right] 代码演示: 今天进行了二分查找的学习。 什么是二分查找 二分查找(Binary Search)是一种常用的搜索算法,也被称为折…...
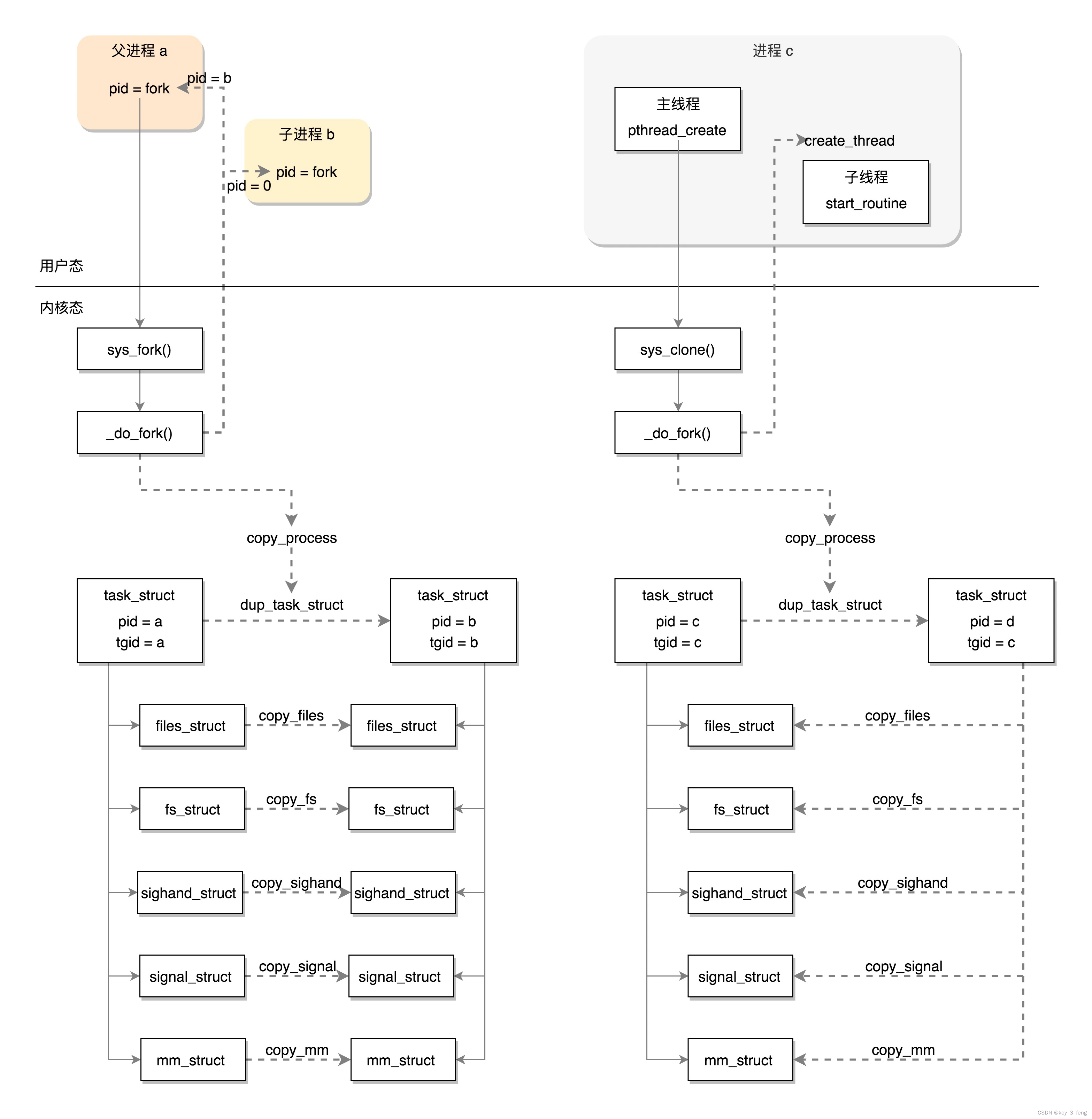
线程是如何创建的
线程不是一个完全由内核实现的机制,它是由内核态和用户态合作完成的。pthread_create 不是一个系统调用,是 Glibc 库的一个函数,所以我们还要去 Glibc 里面去找线索。 首先处理的是线程的属性参数。例如前面写程序的时候,我们设置…...

owl_vit安装步骤
owl项目的clip目录与openai的clip重名了,import时容易找不到文件simple_tokenizer。 from clip import simple_tokenizer解决办法: 把clip项目下的simple_tokenizer.py拷贝到owl项目下的clip文件夹 cp simple_tokenizer.py /{project_dir}/scenic/scenic/projects…...

运行real.exe时出现NUM_METGRID_SOIL_LEVELS=0
本人在运行real.exe时,发现出现这样的报错: d01 2020-01-01_00:00:00 ---- ERROR: Mismatch between namelist and global attribute NUM_METGRID_SOIL_LEVELS NOTE: 2 namelist vs input data inconsistencies found. -------------- FATAL CALL…...

【数值计算方法】Gauss消元法及其Python/C实现
文章目录 一、基础理论1. 线性方程组2. Gauss消元法的详细步骤3. 注意事项 二、具体计算过程1. 用Gauss 消元法求A的LU分解,并由此求解方程组 Ax ba. 将A进行LU分解。b. 使用LU分解求解方程组Axb 三、代码实现1. Python代码实现2. C语言代码实现 Gauss消元法&#x…...

ins老被封禁?快来看看这些雷区你踩了没!
做外贸的小伙伴应该都运营或者接触过Instagram,但是忽视平台规则和操作不当很容易出现ins被封号的情况,今天就给大家介绍ins封禁原因,大家在运营过程中就可以很好避免了! Instagram 封禁原因 1.短时间内大量关注和点赞操作 为了封…...
)
《Effective Java》读书笔记(1-2章)
第一章 创建和销毁对象 1. 考虑用静态代替构造方法 想要获取一个类的实例,一种传统的方式是通过共有的构造器,当然还可以使用另一种技术:提供共有的静态工厂方法。 什么是静态工厂? public static Boolean valueOf(boolean b) …...
函数)
C++版split(‘_‘)函数
目录 1 使用stringstream2 使用双指针算法 1 使用stringstream #include <iostream> #include <sstream> #include <string> #include <vector>using namespace std;vector<string> split(string str, char separator) {vector<string> …...

Leaky singletons的一种使用场景
Leaky singletons的一种使用场景 文章目录 Leaky singletons的一种使用场景场景问题本质如何解决Leaky singletons 场景 最近遇到了这个问题,正好想记录下。 比如你有一段代码,如下(伪代码): static std::map<int…...

TensorFlow图像多标签分类实例
接下来,我们将从零开始讲解一个基于TensorFlow的图像多标签分类实例,这里以图片验证码为例进行讲解。 在我们访问某个网站的时候,经常会遇到图片验证码。图片验证码的主要目的是区分爬虫程序和人类,并将爬虫程序阻挡在外。 下面…...

Python程序设计期末复习笔记
文章目录 一、数据存储1.1 倒计时1.2 os库1.3 字符串操作1.4 文件操作1.5 列表操作1.6 元组1.7 字典 二、文本处理及可视化2.1 jieba分词2.2 集合操作2.3 pdf文件读取2.4 参数传递2.5 变量作用域 三、数据处理分析3.1 Sumpy3.2 Matplotlib3.3 Numpy 四、Pandas4.1 索引操作4.2 …...

人大与加拿大女王大学金融硕士—与您共创辉煌
生活的本质就是有意识的活着,而生活的智慧就是活出了自己想要的样子,那些真正厉害的人,从来都在默默努力,伴随着金融人才的需求日益增长,中国人民大学与加拿大女王大学联合推出了人大女王金融硕士项目,旨在…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
