多分类、正则化问题
多分类问题
利用逻辑回归解决多分类问题,假如有一个训练集,有 3 个类别,分别为三角形 𝑦 = 1,方框𝑦 = 2,圆圈 𝑦 = 3。我们下面要做的就是使用一个训练集,将其分成 3 个二元分类问题。
我们先从用三角形代表的类别 1 开始,此时创造一个新的训练集,三角形为正类,方框和圆圈为负类;
对于方框代表的类别2,此时创造一个新的训练集,方框为正类,三角形和圆圈为负类;
对于圆圈代表的类别3,此时创造一个新的训练集,圆圈为正类,方框和三角形为负类。
过拟合问题
如果模型有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集(代价函数可能几乎为 0),但是可能会不能推广到新的数据集。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HRq07PFu-1677397084341)(C:\Users\20491\AppData\Roaming\Typora\typora-user-images\image-20230225104532799.png)]](https://img-blog.csdnimg.cn/bd93f79f2d4d442695fbadd9fbbe8da9.png)
第一个模型是一个线性模型,欠拟合,不能很好地适应我们的训练集;第三个模型是一
个四次方的模型,过于强调拟合原始数据,而丢失了算法的本质:预测新数据。我们可以看
出,若给出一个新的值使之预测,它将表现的很差,是过拟合,虽然能非常好地适应我们的
训练集但在新输入变量进行预测时可能会效果不好;而中间的模型似乎最合适。
过拟合问题解决方法:
1.丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如 PCA)
2.正则化。 保留所有的特征,但是减少参数的大小(magnitude)。
正则化线性回归
对于上面的图片所示模型,由于高次项导致过拟合的问题,所以通过将高次项的系数接近于0来解决这个问题(即减少θ3、θ4\theta_3、\theta_4θ3、θ4的大小)。通过在θ3、θ4\theta_3、\theta_4θ3、θ4加入惩罚项来减少θ3、θ4\theta_3、\theta_4θ3、θ4的大小。
J(θ0,θ1,...,θn)=12m∑i=1m(hθ(x(i))−y(i))2J(\theta_{0},\theta_{1},...,\theta_{n})=\frac{1}{2m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})^2} J(θ0,θ1,...,θn)=2m1i=1∑m(hθ(x(i))−y(i))2
将上述代价函数改为
J(θ0,θ1,...,θ4)=12m[∑i=1m(hθ(x(i))−y(i))2+1000θ32+10000θ42]J(\theta_{0},\theta_{1},...,\theta_{4})=\frac{1}{2m}[\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})^2}+1000\theta_3^2+10000\theta_4^2] J(θ0,θ1,...,θ4)=2m1[i=1∑m(hθ(x(i))−y(i))2+1000θ32+10000θ42]
假如我们有非常多的特征,我们并不知道其中哪些特征我们要惩罚,我们将对所有的特征进行惩罚,并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设(一般不对θ0\theta_0θ0进行惩罚):
J(θ)=12m[∑i=1m(hθ(x(i))−y(i))2+λ∑j=1nθj2]J(\theta)=\frac{1}{2m}[\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})^2}+\lambda \sum_{j=1}^{n} \theta_j^2] J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
如果选择的正则化参数 λ 过大,则会把所有的参数都最小化了,导致模型变成 Font metrics not found for font: .,也就是图中红色直线所示的情况,造成欠拟合。 因为如果我们令 𝜆 的值很大的话,为了使 Cost Function 尽可能的小,所有的 𝜃 的值(不包括θ0\theta_0θ0)都会在一定程度上减小。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ck5wbVGP-1677397084341)(C:\Users\20491\AppData\Roaming\Typora\typora-user-images\image-20230225111158548.png)]](https://img-blog.csdnimg.cn/1d65a6b5b10e409b9ff7040a8eb3b4e5.png)
对正则化后的代价函数进行梯度下降得到
θ0:=θ0−α1m∑i=1m(hθ(x(i))−y(i))x0(i)\theta_0:=\theta_0-\alpha \frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})}x_0^{(i)} θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))x0(i)
θj:=θj−α[1m∑i=1m(hθ(x(i))−y(i))xj(i)+λmθj]\theta_j:=\theta_j-\alpha[ \frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})}x_j^{(i)}+\frac{\lambda}{m} \theta_j] θj:=θj−α[m1i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj]
整个公式可写为
θj:=θj(1−αλm)−α1m∑i=1m(hθ(x(i))−y(i))xj(i)\theta_j:=\theta_j(1-\alpha \frac{\lambda}{m})-\alpha \frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})}x_j^{(i)} θj:=θj(1−αmλ)−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令𝜃值减少了一个额外的值。
利用正规方程来求解正则化线性回归模型
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hEkfnaGZ-1677397084342)(C:\Users\20491\AppData\Roaming\Typora\typora-user-images\image-20230225112347014.png)]](https://img-blog.csdnimg.cn/6e6d6edda8b54772a73c27608415d63e.png)
正则化逻辑回归模型
J(θ)=1m∑i=1m−y(i)⋅log(hθ(x(i)))−(1−y(i))⋅log(1−hθ(x(i)))+λ2m∑j=1nθj2J({\theta})=\frac{1}{m}\sum_{i=1}^{m}{-y^{(i)}\cdot log(h_{\theta}(x^{(i)}))-(1-y^{(i)})\cdot log(1-h_{\theta}(x^{(i)}))}+\frac{\lambda}{2m}\sum_{j=1}^{n} \theta_j^2 J(θ)=m1i=1∑m−y(i)⋅log(hθ(x(i)))−(1−y(i))⋅log(1−hθ(x(i)))+2mλj=1∑nθj2
该代价函数的梯度下降算法为
θ0:=θ0−α1m∑i=1m(hθ(x(i))−y(i))x0(i)\theta_0:=\theta_0-\alpha \frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})}x_0^{(i)} θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))x0(i)
θj:=θj−α[1m∑i=1m(hθ(x(i))−y(i))xj(i)+λmθj]\theta_j:=\theta_j-\alpha[ \frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})}x_j^{(i)}+\frac{\lambda}{m} \theta_j] θj:=θj−α[m1i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj]
相关文章:
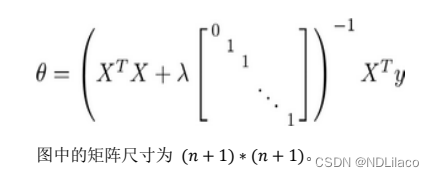
多分类、正则化问题
多分类问题 利用逻辑回归解决多分类问题,假如有一个训练集,有 3 个类别,分别为三角形 𝑦 1,方框𝑦 2,圆圈 𝑦 3。我们下面要做的就是使用一个训练集,将其分成 3 个二…...

史上最全面的软件测试面试题总结(接口、自动化、性能全都有)
目录 思维发散 Linux 测试概念和模型 测试计划与工具 测试用例设计 Web项目 Python基础 算法 逻辑 接口测试 性能测试 总结感谢每一个认真阅读我文章的人!!! 重点:配套学习资料和视频教学 思维发散 一个球ÿ…...

速来~与 Werner Vogels 博士一起探索敏捷性与创新速度一起提升的秘方
Amazon Web Services 的现代应用程序创新一直是 Amazon 公司坚持追求的核心目标。约20年前,我们经历了一次彻底的转型,旨在建立起“发明、发布、再发明、再发布、重新开始、洗牌、再重复”的快速迭代流程。正是此番探索,彻底改变了我们构建应…...

Apache Hadoop、HDFS介绍
目录Hadoop介绍Hadoop集群HDFS分布式文件系统基础文件系统与分布式文件系统HDFS简介HDFS shell命令行HDFS工作流程与机制HDFS集群角色与职责HDFS写数据流程(上传文件)HDFS读数据流程(下载文件)Hadoop介绍 用Java语言实现开源 允许…...
python“r e 模块“常见函数详解
正则表达式:英文Regular Expression,是计算机科学的一个重要概念,她使用一种数学算法来解决计算机程序中的文本检索,匹配等问题,正则表达式语言是一种专门用于字符串处理的语言。在很多语言中都提供了对它的支持,re模块…...

【数据结构】二叉树的四种遍历方式——必做题
写在前面学完上一篇文章的二叉树的遍历之后,来尝试下面的习题吧开始做题144. 二叉树的前序遍历 - 力扣(LeetCode)94. 二叉树的中序遍历 - 力扣(LeetCode)145. 二叉树的后序遍历 - 力扣(LeetCode)…...

Nginx使用“逻辑与”配置origin限制,修复CORS跨域漏洞
目录1.漏洞报告2.漏洞复现3.Nginx 修复3.1 添加请求头3.2 配置origin限制2.3 调整origin限制1.漏洞报告 漏洞名称: CORS 跨域漏洞等级: 中危漏洞证明: Origin从任何域名都可成功访问,未做任何限制。漏洞危害: 因为同源…...
Laravel框架02:路由与控制器
Laravel框架02:路由与控制器一、路由配置文件二、路由参数三、路由别名四、路由群组五、控制器概述六、控制器路由七、接收用户输入一、路由配置文件 以web网页路由文件为例: 默认根路由 路由定义格式Route::请求方式(请求的URL, 匿名函数或控制响应的方…...
)
【POJ 2418】Hardwood Species 题解(映射)
描述 阔叶树是一种植物群,具有宽阔的叶子,结出果实或坚果,通常在冬天休眠。 美国的温带气候造就了数百种阔叶树种的森林,这些树种具有某些生物特征。例如,虽然橡树、枫树和樱桃都是硬木树,但它们是不同的物…...
)
React组件之间的通信方式总结(下)
一、写一个时钟 用 react 写一个每秒都可以更新一次的时钟 import React from react import ReactDOM from react-domfunction tick() {let ele <h1>{ new Date().toLocaleTimeString() }</h1>// Objects are not valid as a React child (found: Sun Aug 04 20…...
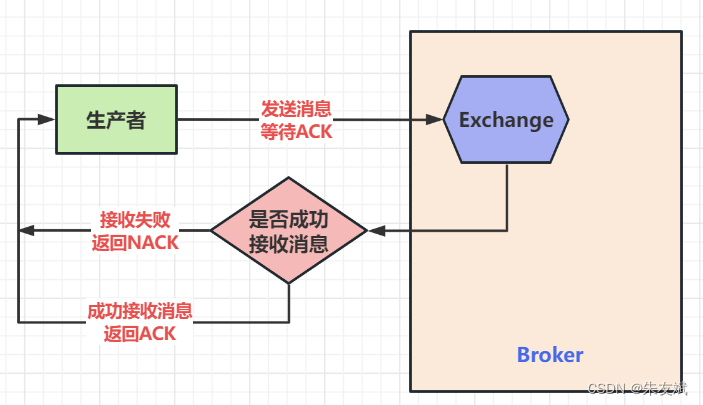
【RabbitMQ笔记07】消息队列RabbitMQ七种模式之Publisher Confirms发布确认模式
这篇文章,主要接收消息队列RabbitMQ七种模式之Publisher Confirms发布确认模式。 目录 一、消息队列 1.1、发布确认模式 1.2、案例代码 (1)引入依赖 (2)编写生产者【消息确认--单条确认】 (3…...

【华为OD机试模拟题】用 C++ 实现 - IPv4 地址转换成整数(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 去重求和(2023.Q1) 文章目录 最近更新的博客使用说明IPv4 地址转换成整数题目输入输出示例一输入输出说明示例一输入输出说明Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,...

闭包与高阶函数
文中内容均来自于曾探《JavaScript设计模式与开发实践》的学习笔记。闭包作用域变量的作用域,就是指变量的有效范围。局部变量、全局变量。变量的搜索是从内到外而非从外到内的。变量的生命周期对于全局变量莱索,全局变量的生命周期是永久的,…...

人工智能轨道交通行业周刊-第35期(2023.2.20-2.26)
本期关键词:重庆智慧轨道、智能运维主机、标准轨距、地方铁路公报、景深、机器视觉应用 1 整理涉及公众号名单 1.1 行业类 RT轨道交通人民铁道世界轨道交通资讯网铁路信号技术交流北京铁路轨道交通网上榜铁路视点ITS World轨道交通联盟VSTR铁路与城市轨道交通Rai…...

快慢指针判断链表是否有环
快慢指针判断链表是否有环 单链表有可能存在环,有些情况下要判断一个单链表是否有环。数组的有个快慢指针的方法,其实单链表和数组有相似的地方,可以使用快慢指针的方法。具体做法如下: 首先创建两个指针,它们初始时…...

《MongoDB入门教程》第26篇 聚合统计之$max/$min表达式
本文将会介绍两个 MongoDB 表达式,返回一组数据中最大值的 $max 表达式,以及返回一组数据中最小值的 $min 表达式。 $max 表达式 $max 表达式用于返回一组数据中的最大值,语法如下: { $max: <expression> }$max 表达式在…...

FPGA纯verilog解码SDI视频 纯逻辑资源实现 提供2套工程源码和技术支持
目录1、前言2、硬件电路解析SDI摄像头Gv8601a单端转差GTX解串SDI解码VGA时序恢复YUV转RGB图像输出FDMA图像缓存HDMI输出3、工程1详解:无缓存输出4、工程2详解:缓存3帧输出5、上板调试验证并演示6、福利:工程代码的获取1、前言 FPGA实现SDI视…...
JVM篇之垃圾回收
一.如何判断对象可以回收 1.引用计数法 只要一个对象被其他变量所引用,就让它的计数加1,被引用了两次就让它的计数变成2,当这个变量的计数变成0时,就可以被垃圾回收; 弊端:当出现如下图的情况࿰…...

尝试用程序计算Π(3.141592653......)
文章目录1. π\piπ2. 用微积分来计算π\piπ2.1 原理2.2 代码2.3 结果2.4 分析1. π\piπ π\piπ的重要性或者地位不用多说,有时候还是很好奇,精确地π\piπ值是怎么计算出来的。研究π\piπ的精确计算应该是很多数学家计算机科学家努力的方向…...

【异常检测三件套】系列3--时序异常检测综述
写在前面: 异常检测共包含3个内容,从多个方面剖析异常检测方法,本文为第三篇。过往内容请查看以下链接: 【异常检测三件套】系列1--14种异常检测算法https://blog.csdn.net/allein_STR/article/details/128114175?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
