尝试用程序计算Π(3.141592653......)
文章目录
- 1. π\piπ
- 2. 用微积分来计算π\piπ
- 2.1 原理
- 2.2 代码
- 2.3 结果
- 2.4 分析
1. π\piπ
π\piπ的重要性或者地位不用多说,有时候还是很好奇,精确地π\piπ值是怎么计算出来的。研究π\piπ的精确计算应该是很多数学家计算机科学家努力的方向,很多算式看起来和π\piπ没有一点关系,但是最后的表达式中却包含π\piπ。
作为一个国家定义的从事信息技术的“新时代农民工”,要验证某些式子相对来说就容易得多了。
2. 用微积分来计算π\piπ
2.1 原理
小学时候就知道了圆的面积公式S=πr2S=\pi r^2S=πr2,到了高中学习了微积分,方程与曲线之后可以知道:
x2+y2=r2x^2 + y^2 = r^2x2+y2=r2
表示一个圆,如果y>=0y>=0y>=0则表示上半圆,这个时候上半圆可以表达为一个函数:
y=(r2−x2)y = \sqrt{(r^2-x^2)}y=(r2−x2)
当它是一个单位圆时(r=1)图形如下所示:

根据从微积分的角度来看曲线y(x)与x=0,x∈[−r,r]y(x)与x=0,x\in [-r,r]y(x)与x=0,x∈[−r,r]围成的区域面积,就是圆面积的一半,即上半圆的面积。令圆面积为S,则有:令圆面积为S,则有:令圆面积为S,则有:
S=πr2=2∫−rr(r2−x2)dxS = \pi r^2 = 2\int_{-r}^{r} \sqrt{(r^2-x^2)} dxS=πr2=2∫−rr(r2−x2)dx
现在的工作就变成计算上面右侧的积分式了。积分式用化曲为直(马师傅称为:接 化 发),把圆分成许多直立的小矩形,再求和,小矩形的高为yi=(r2−xi2),宽为Δx,Δx=1ny_i=\sqrt{(r^2-x_{i}^2)},宽为\Delta x, \Delta x=\frac{1}{n}yi=(r2−xi2),宽为Δx,Δx=n1,n表示把圆的面积分为n个小矩形的面积来近似,n越大则近似程度越好,而且当n趋近于无穷时就和积分式完全一致了。
为了求π\piπ那我们只需要用程序帮我们把圆分成一个一个的小矩形再求和就行了,设定圆的半径,每个矩形的宽度,就可以计算积分式的近似值了。
下面的程序就来计算下式
π=2r2∫−rr(r2−x2)dx\pi = \frac{2}{r^2}\int_{-r}^{r} \sqrt{(r^2-x^2)} dxπ=r22∫−rr(r2−x2)dx
2.2 代码
#include <cmath>
#include <iostream>/*** @brief calculate sqrt(r^2-x^2)* * @param x : * @return constexpr long double */
constexpr inline long double IntegralFormula(const long double radius,const long double x)
{return std::sqrt(radius*radius-x*x);
} /*** @brief 计算曲线y=sqrt(r^2-x^2),在 x in [-r,r]的积分* * @param radius : * @param delta_x : * @return constexpr long double */
constexpr long double Integral(const long double radius,const long double delta_x)
{long double sum = 0.0;for (double x = -radius; x <= radius; x += delta_x){sum += delta_x * IntegralFormula(radius,x);}return sum;
}/*** @brief * * @param radius : 半径* @param bin_num : 分成小矩形的数目* @return constexpr long double */
constexpr long double CalculatePi(const long double radius,double bin_num)
{long double delta_x = 2 * radius / bin_num;long double integral = Integral(radius,delta_x);long double pi = integral * 2.0 / (radius * radius);return pi;
}/*** @brief 计算pi值,用单位圆的上半圆做积分,y=sqrt(r^2-x^2),x in [-r,r]* */
void Test()
{constexpr long double true_pi = 3.141592653589793;printf("True PI: %.15Lf\n",true_pi);for(double radius = 10; radius <= 100; radius*=10)for(double bin_num = 100000; bin_num <= 10000000; bin_num*=10){printf("radius:%f, \t bin_num: %f,\t pi: %.20Lf \n",radius,bin_num,CalculatePi(radius,bin_num));}}void Test2()
{double radius = 10000;double bin_num = 100000;printf("radius:%f, \t bin_num: %f,\t pi: %.20Lf \n",radius,bin_num,CalculatePi(radius,bin_num));
}int main()
{Test();Test2();return 0;
}
2.3 结果
输出
True PI: 3.141592653589793
radius:10.000000, bin_num: 100000.000000, pi: 3.14159254840509465393
radius:10.000000, bin_num: 1000000.000000, pi: 3.14159265028029712060
radius:10.000000, bin_num: 10000000.000000, pi: 3.14159265331958147799
radius:100.000000, bin_num: 100000.000000, pi: 3.14159254846500206543
radius:100.000000, bin_num: 1000000.000000, pi: 3.14159265024260935645
radius:100.000000, bin_num: 10000000.000000, pi: 3.14159265331696711159
radius:10000.000000, bin_num: 100000.000000, pi: 3.141592548407530979602.4 分析
这重方式用long double的计算精度,但是最后计算的精度最高只到"3.141592653",小数点后9位。分再多的小矩形也没用了,因为计算时候的截断误差已经足够影响计算精度了。不知道有没有什么好的策略保持计算精度的。
相关文章:

尝试用程序计算Π(3.141592653......)
文章目录1. π\piπ2. 用微积分来计算π\piπ2.1 原理2.2 代码2.3 结果2.4 分析1. π\piπ π\piπ的重要性或者地位不用多说,有时候还是很好奇,精确地π\piπ值是怎么计算出来的。研究π\piπ的精确计算应该是很多数学家计算机科学家努力的方向…...

【异常检测三件套】系列3--时序异常检测综述
写在前面: 异常检测共包含3个内容,从多个方面剖析异常检测方法,本文为第三篇。过往内容请查看以下链接: 【异常检测三件套】系列1--14种异常检测算法https://blog.csdn.net/allein_STR/article/details/128114175?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%…...

关于SAP 错误日志解析
有时候启动或操作sap会出现故障,只是察看sap用户当前目录下的日志文件可能不得要领,此时有必要察看work目录下的一些trace. 以Linux系统为例,其他的也差不多。 instance说明 如下 DVEBMGS?? ABAP Central Instance D?? …...
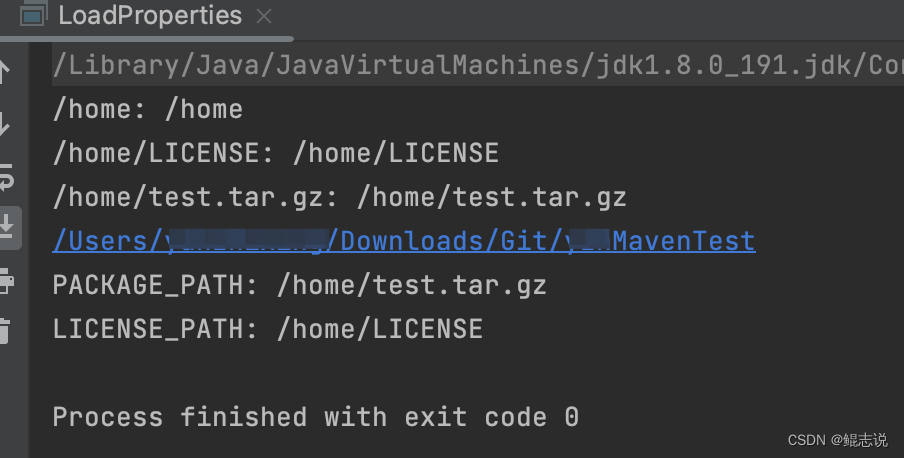
java:自定义变量加载到系统变量后替换shell模版并执行shell
这里的需求前提是,在项目中进行某些操作前,需要在命令后对shell配置文件的进行修改(如ip、port),这个对于用户是不友好的,需要改为用户页面输入ip、port,后台自动去操作修改配置;那么…...
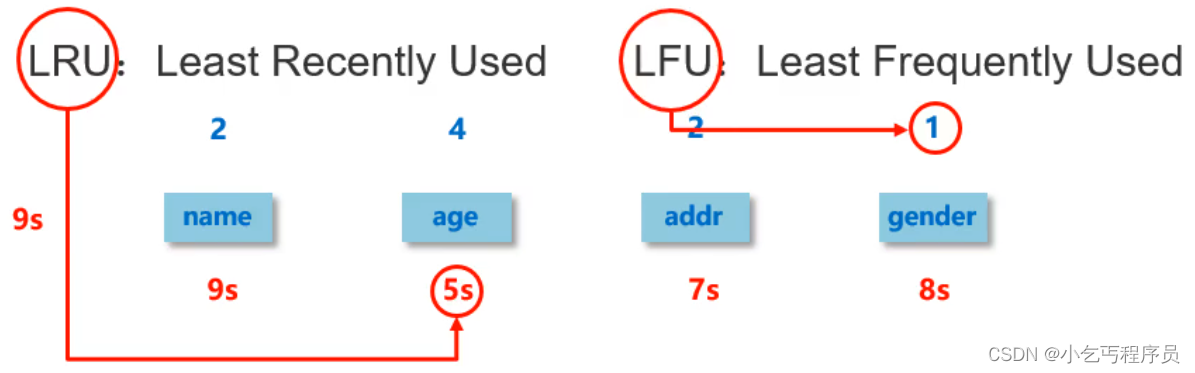
Redis高级删除策略与数据淘汰
第二章:Redis高级 学习目标 目标1:能够说出redis中的数据删除策与略淘汰策略 目标2:能够说出主从复制的概念,工作流程以及场景问题及解决方案 目标3:能够说出哨兵的作用以及工作原理,以及如何启用哨兵 …...
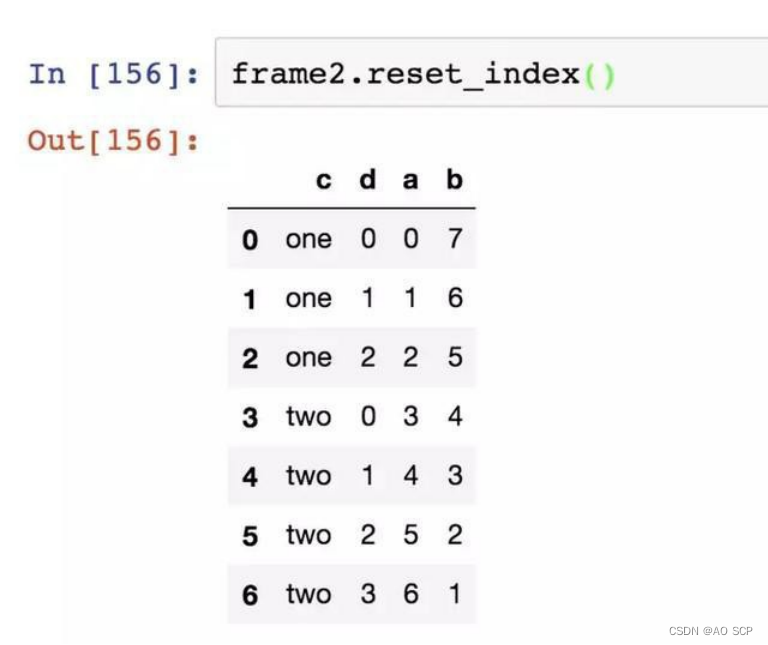
社畜大学生的Python之pandas学习笔记,保姆入门级教学
接上期,上篇介绍了 NumPy,本篇介绍 pandas。 目录 pandas 入门pandas 的数据结构介绍基本功能汇总和计算描述统计处理缺失数据层次化索引 pandas 入门 Pandas 是基于 Numpy 构建的,让以 NumPy 为中心的应用变的更加简单。 Pandas是基于Numpy…...
20_FreeRTOS低功耗模式
目录 低功耗模式简介 STM32低功耗模式 Tickless模式详解 Tickless模式相关配置 实验源码 低功耗模式简介 很多应用场合对于功耗的要求很严格,比如可穿戴低功耗产品、物联网低功耗产品等。 一般MCU都有相应的低功耗模式,裸机开发时可以使用MCU的低功耗模式。 FreeRTOS也…...

Hive的使用方式
操作Hive可以在Shell命令行下操作,或者是使用JDBC代码的方式操作 针对命令行这种方式,其实还有两种使用 第一个是使用bin目录下的hive命令,这个是从hive一开始就支持的使用方式 后来又出现一个beeline命令,它是通过HiveServer2服…...

Flume三大核心组件
Flume的三大核心组件: Source:数据源 Channel:临时存储数据的管道 Sink:目的地 Source:数据源:通过source组件可以指定让Flume读取哪里的数据,然后将数据传递给后面的 channel Flume内置支持读…...
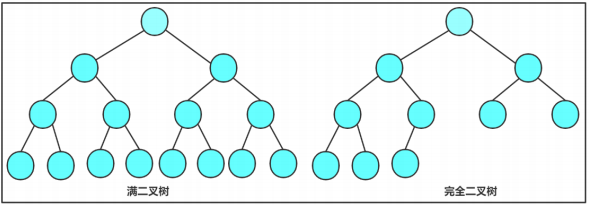
数据结构(六)二叉树
一、树形结构概念树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:1、有一个…...
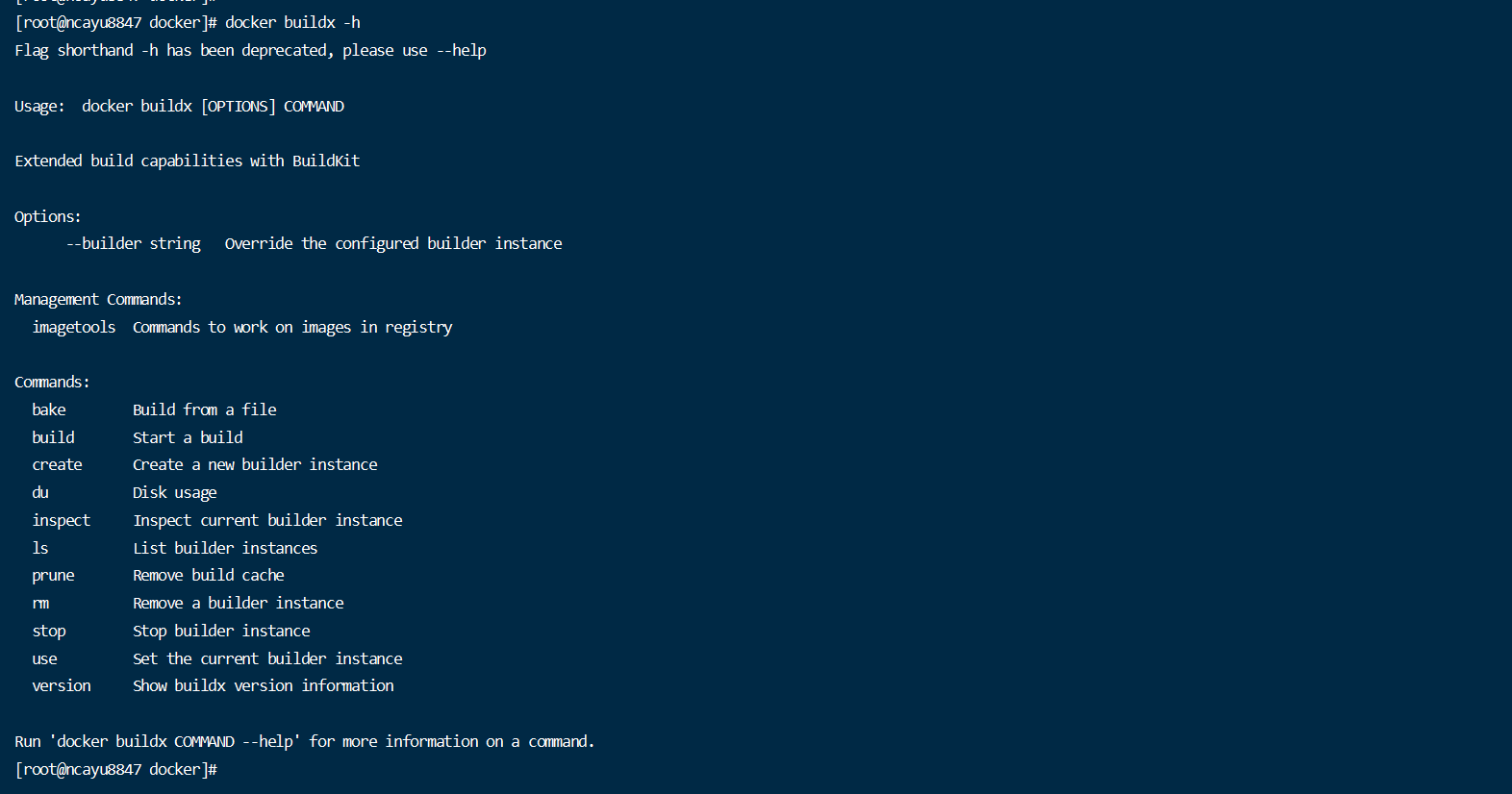
Docker buildx 的跨平台编译
docker buildx 默认的 docker build 命令无法完成跨平台构建任务,我们需要为 docker 命令行安装 buildx 插件扩展其功能。buildx 能够使用由 Moby BuildKit 提供的构建镜像额外特性,它能够创建多个 builder 实例,在多个节点并行地执行构建任…...

【java基础】方法重载和方法重写
文章目录方法重载方法重写方法重载 方法重载就是可以在一个类里面定义多个相同名称的方法,只需要参数列表的个数或者类型不同就行。 public class Overload {public int add(int a, int b) {return a b;}public double add(double a, double b) {return a b;}}对…...
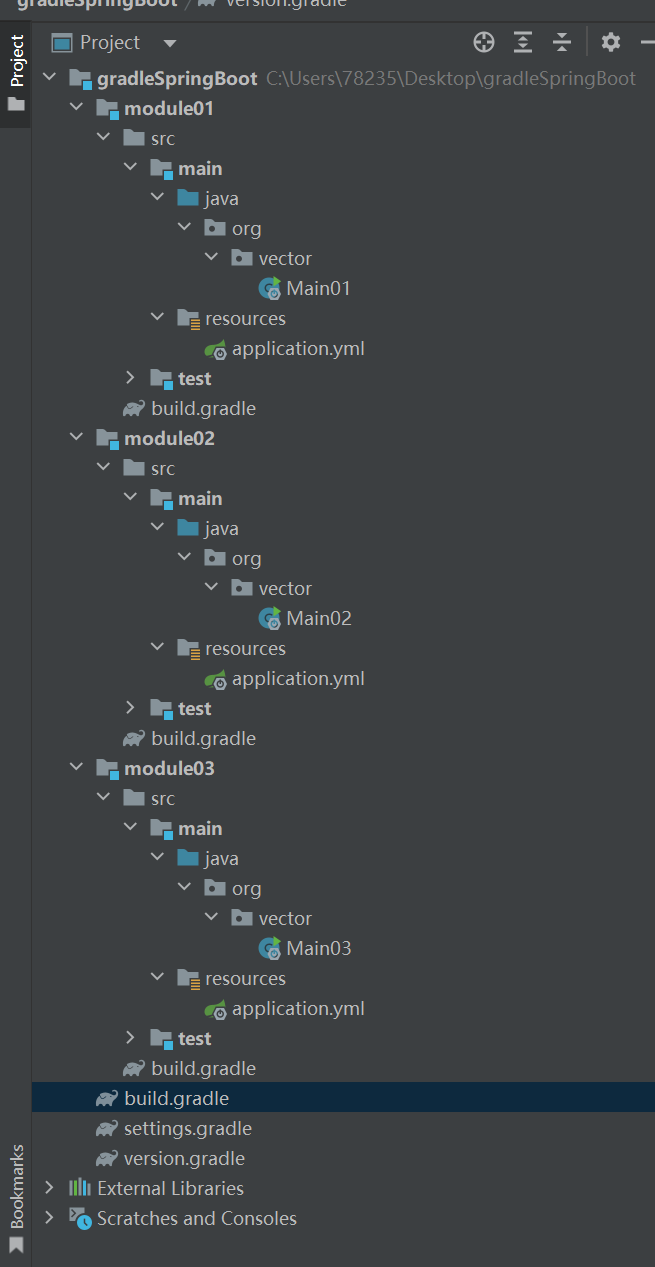
Gradle7.4安装与基本使用
文章目录一.前言二.下载Gradle三.Gradle镜像源-全局级配置四.配置Gradle wrapper-项目级配置五.Gradle对测试的支持五.生命周期5.1 settings文件六.Gradle任务入门6.1 任务行为6.2 任务依赖方式七. Dependencies依赖引入7.1 依赖冲突及解决方案八.Gradle整合多模块SpringBoot九…...

[系统安全] 虚拟化安全之虚拟化概述
本文为笔者从零基础学习系统安全相关内容的笔记,如果您对系统安全、逆向分析等内容感兴趣或者想要了解一些内容,欢迎关注。本系列文章将会随着笔者在未来三年的读研过程中持续更新,由于笔者现阶段还处于初学阶段,不可避免参照复现各类书籍内容,如书籍作者认为侵权请告知,…...

如何从零开始系统的学习项目管理?
经常会有人问,项目管理到底应该学习一些什么?学习考证之后能得到什么价值? 以下我就总结一下内容 一,学习项目管理有用吗? 有效的项目管理带来的益处大致包括以下几个方面:更有效达成业务目标、满足相关…...

面试题-----
面试题---- 一.HTML 1.常用哪些浏览器进行测试,对应有哪些内核? ①IE------------------->Trident ②Chrome---------->以前是Webkit现在是Blink ③Firefox------------>Gecko ④Safari-------------->Webkit ⑤Opera--------------&…...
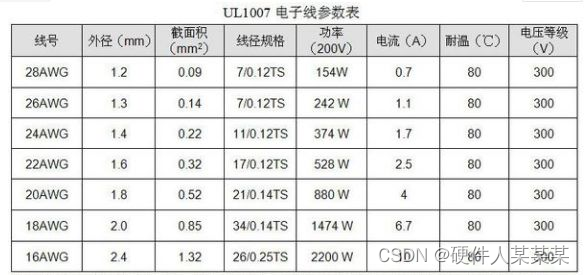
线材-电子线载流能力
今天来讲的是关于电子线的一个小知识,可能只做板子的工程师遇到此方面的问题会比较少,做整机的工程师则必然会遇到此方面问题,那就是线材问题。 下面主要说下电子线的过电流能力。(文末有工具下载)电子线(h…...
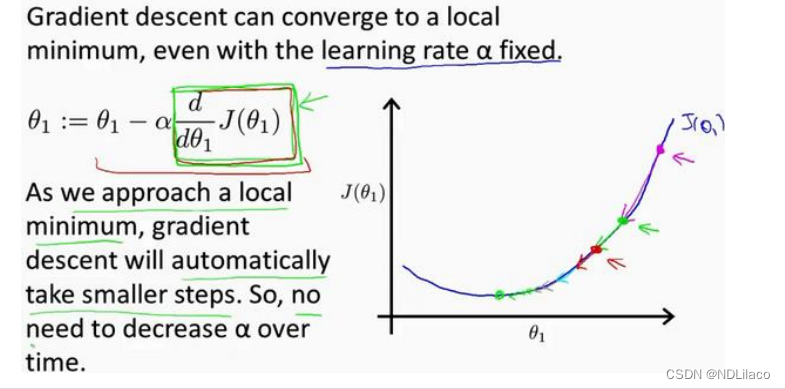
单变量回归问题
单变量回归问题 对于某房价问题,x为房屋大小,h即为预估房价,模型公式为: hθ(x)θ0θ1xh_{\theta}(x)\theta_{0}\theta_{1}x hθ(x)θ0θ1x 要利用训练集拟合该公式(主要是计算θ0、θ1\theta_{0}、\theta_{1}θ…...
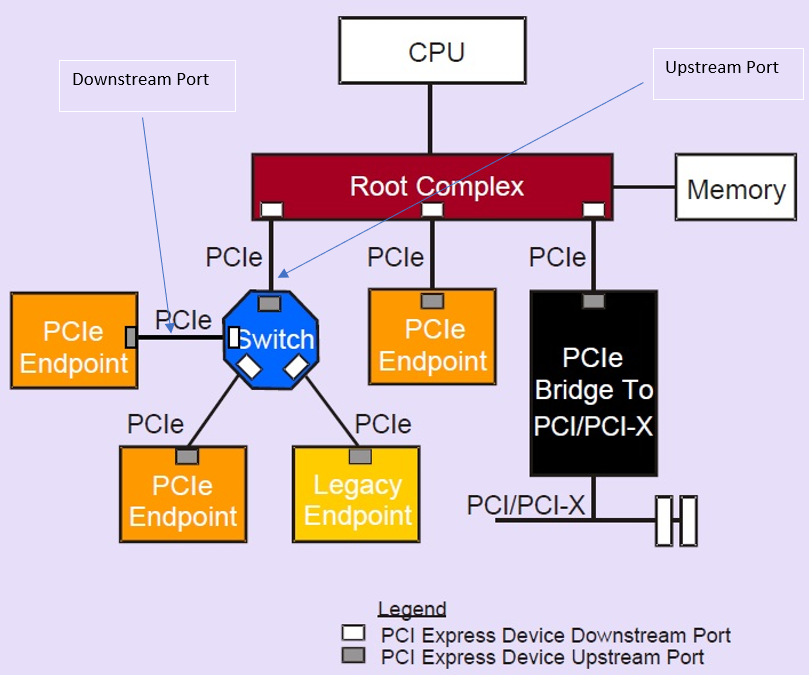
ubuntu/linux系统知识(36)linux网卡命名规则
文章目录背景命名规范系统默认命名规则优势背景 很久以前Linux 操作系统的网卡设备的传统命名方式是 eth0、eth1、eth2等,属于biosdevname 命名规范。 服务器通常有多块网卡,有板载集成的,同时也有插在PCIe插槽的。Linux系统的命名原来是et…...
java的一些冷知识
接口并没有继承Object类首先接口是一种特殊的类,理由就是将其编译后是一个class文件大家都知道java类都继承自Object,但是接口其实是并没有继承Object类的 可以自己写代码测试: 获取接口类的class对象后遍历它的methods,可以发现是不存在Obje…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...
