ccc-台大林轩田机器学习基石-hw1
文章目录
- Question1-14
- Question15-PLA
- Question16-PLA平均迭代次数
- Question17-不同迭代系数的PLA
- Question18-Pocket_PLA
- Question19-PLA的错误率
- Question20-修改Pocket_PLA迭代次数
Question1-14

对于有明确公式和定义的不需要使用到ml

智能系统在与环境的连续互动中学习最优行为策略的机器学习问题,学习最优的序贯决策

无标签分类
从标注数据 学习预测模型

主动地提出一些标注请求,将一些经过筛选的数据提交给专家进行标注

- 解题关键是计算N+1到N+L上的偶数个数
- 0到N的偶数个数是⌊N⌋2\frac{ ⌊N⌋}{2}2⌊N⌋
- 问题转化成(0到N+L的偶数个数-0到N的偶数个数)

generate了D,但是N+1到N+L上L个点没有generate。每个点都有{被generate,没被generate}两种可能,所以是2L2^L2L

由“无免费午餐定理”可知,任何算法在没有噪声时对于未知样本期望相等

P(5orange&5else)=C105210P(5orange\&5else)=\frac{C_{10}^5}{2^{10}}P(5orange&5else)=210C105
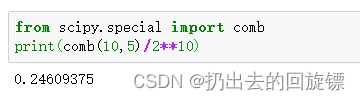
from scipy.special import comb
print(comb(10,5)/2**10)

P(9orange&1else)=C1090.99×0.1P(9orange\&1else)=\frac{C_{10}^9}{0.9^{9}\times0.1}P(9orange&1else)=0.99×0.1C109
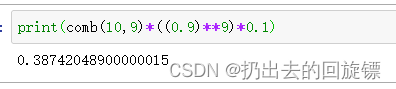
print(comb(10,9)*((0.9)**9)*0.1)

- 分v=0.1和0时讨论
P=C101(910)1(110)9+C100(110)10P=C_{10}^1{(\frac 9{10})^{1}{(\frac 1 {10})}^{9} }+C_{10}^0{{(\frac 1 {10})}^{10}}P=C101(109)1(101)9+C100(101)10


Hoeffding:P[∣μ−v∣>ϵ]≤2e−2ϵ2NP[v≤0.1]=P[0.9−v≥0.8]=P[μ−v≥0.8]≤P[∣μ−v∣≥0.8]≤2e−2×0.82×10≈5.5215451440744015×10−6Hoeffding:\mathbb P[| \mu-v|>\epsilon]\le 2e^{-2\epsilon ^2N}\\ \begin{aligned} \mathbb P[v\le 0.1] &=P[0.9-v\ge 0.8]\\ &=P[\mu-v\ge 0.8]\\ &\le P[|\mu-v|\ge 0.8]\\ &\le 2e^{-2\times 0.8^2\times 10}\\ &\approx5.5215451440744015\times 10^{-6} \end{aligned}Hoeffding:P[∣μ−v∣>ϵ]≤2e−2ϵ2NP[v≤0.1]=P[0.9−v≥0.8]=P[μ−v≥0.8]≤P[∣μ−v∣≥0.8]≤2e−2×0.82×10≈5.5215451440744015×10−6

- A:奇数绿,偶数橙
- B:奇数橙,偶数绿
- C:1-3橙,4-6绿
- D:1-3绿,4-6橙
5个橙1,只可能是BC中,所以132=8256\frac{1}{32}=\frac{8}{256}321=2568

- 1全橙:BC
- 2全橙:AC
- 3全橙:BC
- 4全橙:AD
- 5全橙:BD
- 6全橙:AD
- 全A,B,C,D被重复算了一遍,要减去4
P=4×25−445=31256P=\frac{4\times2^5-4}{4^5}=\frac {31}{256}P=454×25−4=25631

Question15-PLA

data链接

代码部分:
utils函数:
import numpy as np
#判别函数,判断所有数据是否分类完成
def Judge(X, y, w):n = X.shape[0]num = np.sum(X.dot(w) * y > 0)return num == ndef PLA(X, y, eta=1, max_step=np.inf):# 获取维度n, d = X.shape# 初始化w = np.zeros(d)# 迭代次数t = 0# 元素的下标i = 0# 错误的下标last = 0while not (Judge(X, y, w)) :if np.sign(X[i, :].dot(w) * y[i]) <= 0:t += 1w += eta * y[i] * X[i, :]# 更新错误last = i# 移动到下一个元素,如果达到n,则重置为0i += 1if i == n:i = 0return t, last, w
主函数:
import numpy as np
import utils as util#读取数据
data = np.genfromtxt("hw1_15_train.dat")
#获取维度
n, d = data.shape
#分离X
X = data[:, :-1]
#添加偏置项1
X = np.c_[np.ones(n), X]
#分离y
y = data[:, -1]
print(util.PLA(X, y))
运行结果:

Question16-PLA平均迭代次数

代码部分:
utils函数:
import numpy as np
import matplotlib.pyplot as pltdef Judge(X, y, w):n = X.shape[0]num = np.sum(X.dot(w) * y > 0)return num == ndef PLA(X, y, eta=1):n, d = X.shapew = np.zeros(d)t = 0i = 0last = 0while not (Judge(X, y, w)):if np.sign(X[i, :].dot(w) * y[i]) <= 0:t += 1w += eta * y[i] * X[i, :]last = ii += 1if i == n:i = 0return t, last, w#运行g算法n次并返回平均的迭代次数
def average_of_n(g, X, y, n, eta=1):result = []data = np.c_[X, y]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]result.append(g(X, y, eta=eta)[0])plt.hist(result)plt.xlabel("迭代次数")plt.title("平均运行次数为" + str(np.mean(result)))plt.show()
主函数:
import numpy as np
import utils as util
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False #显示负号data = np.genfromtxt("hw1_15_train.dat")
#获取维度
n, d = data.shape
#分离X
X = data[:, :-1]
#添加偏置项1
X = np.c_[np.ones(n), X]
#分离y
y = data[:, -1]
util.average_of_n(util.PLA, X, y, 2000, 1)
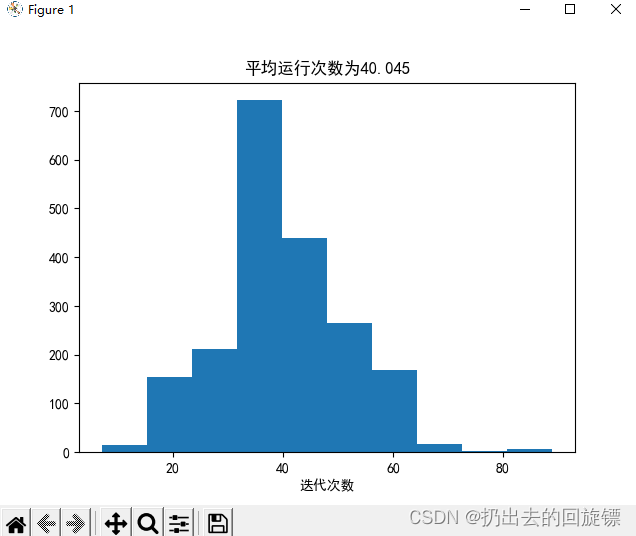
Question17-不同迭代系数的PLA
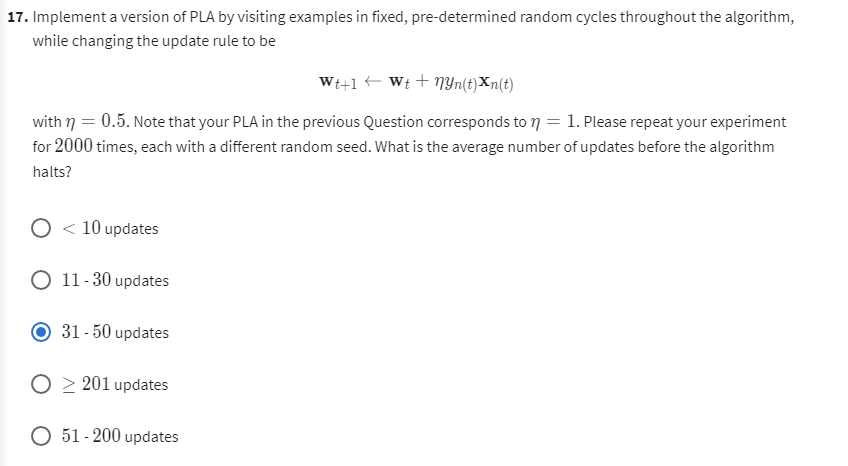
修改迭代系数即可:
util.average_of_n(util.PLA, X, y, 2000, 0.5)
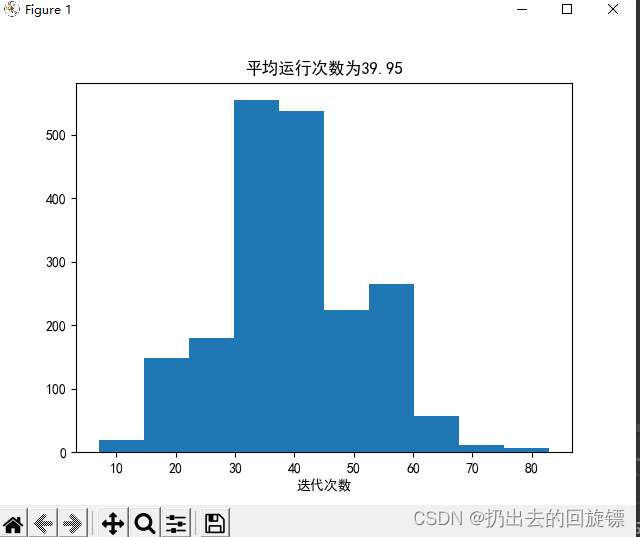
Question18-Pocket_PLA
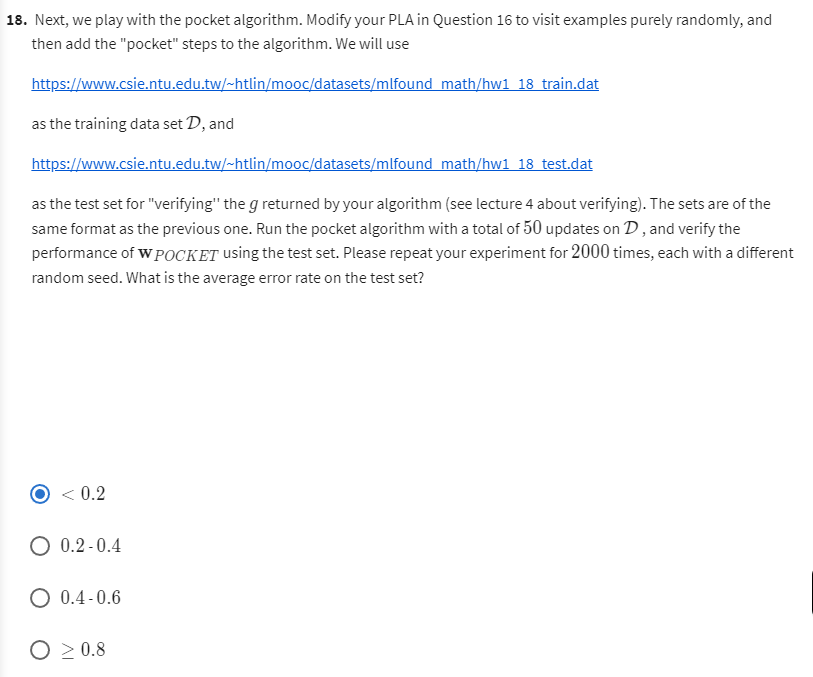
utils函数:
import matplotlib.pyplot as plt
import numpy as np
#统计错误数量
def count(X, y, w):num = np.sum(X.dot(w) * y <= 0)return np.sum(num)#预处理
def preprocess(data):# 获取维度n, d = data.shape# 分离XX = data[:, :-1]# 添加偏置项1X = np.c_[np.ones(n), X]# 分离yy = data[:, -1]return X, ydef Pocket_PLA(X, y, eta=1, max_step=np.inf):#max_step 限制迭代次数#获得数据维度n, d = X.shape#初始化w = np.zeros(d)#记录最优向量w0 = np.zeros(d)#记录次数t = 0#记录最少错误数量error = count(X, y, w0)#记录元素的下标i = 0while (error != 0 and t < max_step):if np.sign(X[i, :].dot(w) * y[i]) <= 0:w += eta * y[i] * X[i, :]#迭代次数增加t += 1#记录当前错误error_now = count(X, y, w)if error_now < error:error = error_noww0 = np.copy(w)#移动到下一个元素i += 1#如果达到n,则重置为0if i == n:i = 0return error, w0#运行g算法n次,1代表训练集,2代表测试集
def average_of_n(g, X1, y1, X2, y2, n, eta=1, max_step=np.inf):result = []data = np.c_[X1, y1]m = X2.shape[0]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]w = g(X, y, eta=eta, max_step=max_step)[-1]result.append(count(X2, y2, w) / m)plt.hist(result)plt.xlabel("错误率")plt.title("平均错误率为"+str(np.mean(result)))plt.show()
主函数:
import matplotlib.pyplot as plt
import numpy as np
import utils as util
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号data_train = np.genfromtxt("hw1_18_train.dat")
data_test = np.genfromtxt("hw1_18_test.dat")X_train, y_train = util.preprocess(data_train)
X_test, y_test = util.preprocess(data_test)util.average_of_n(util.Pocket_PLA, X_train, y_train, X_test, y_test, 2000, max_step=50)
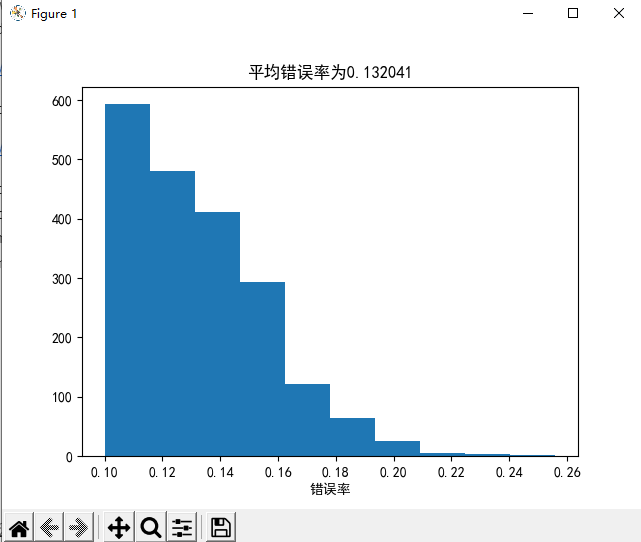
Question19-PLA的错误率

utils函数:
import matplotlib.pyplot as plt
import numpy as npdef count(X, y, w):#判断是否同号num = np.sum(X.dot(w) * y <= 0)return np.sum(num)def Judge(X, y, w):n = X.shape[0]#判断是否同号num = np.sum(X.dot(w) * y > 0)return num == ndef preprocess(data):"""数据预处理"""# 获取维度n, d = data.shape# 分离XX = data[:, :-1]# 添加偏置项1X = np.c_[np.ones(n), X]# 分离yy = data[:, -1]return X, ydef PLA(X, y, eta=1,max_step=np.inf):n, d = X.shapew = np.zeros(d)t = 0i = 0last = 0while not (Judge(X, y, w)) and t<max_step:if np.sign(X[i, :].dot(w) * y[i]) <= 0:t += 1w += eta * y[i] * X[i, :]last = ii += 1if i == n:i = 0return t, last, w#运行g算法n次,1代表训练集,2代表测试集
def average_of_n(g, X1, y1, X2, y2, n, eta=1, max_step=np.inf):result = []data = np.c_[X1, y1]m = X2.shape[0]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]w = g(X, y, eta=eta, max_step=max_step)[-1]result.append(count(X2, y2, w) / m)plt.hist(result)plt.xlabel("错误率")plt.title("平均错误率为"+str(np.mean(result)))plt.show()
主函数:
import matplotlib.pyplot as plt
import numpy as np
import utils as util
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号data_train = np.genfromtxt("hw1_18_train.dat")
data_test = np.genfromtxt("hw1_18_test.dat")X_train, y_train = util.preprocess(data_train)
X_test, y_test = util.preprocess(data_test)util.average_of_n(util.PLA, X_train, y_train, X_test, y_test, 2000, max_step=50)
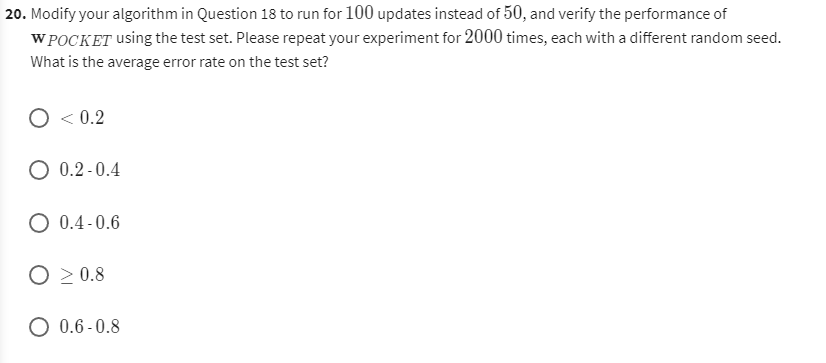
Question20-修改Pocket_PLA迭代次数
utils函数:
import matplotlib.pyplot as plt
import numpy as npdef count(X, y, w):#判断是否同号num = np.sum(X.dot(w) * y <= 0)return np.sum(num)def Judge(X, y, w):n = X.shape[0]#判断是否同号num = np.sum(X.dot(w) * y > 0)return num == ndef preprocess(data):"""数据预处理"""# 获取维度n, d = data.shape# 分离XX = data[:, :-1]# 添加偏置项1X = np.c_[np.ones(n), X]# 分离yy = data[:, -1]return X, ydef Pocket_PLA(X, y, eta=1, max_step=np.inf):#max_step 限制迭代次数#获得数据维度n, d = X.shape#初始化w = np.zeros(d)#记录最优向量w0 = np.zeros(d)#记录次数t = 0#记录最少错误数量error = count(X, y, w0)#记录元素的下标i = 0while (error != 0 and t < max_step):if np.sign(X[i, :].dot(w) * y[i]) <= 0:w += eta * y[i] * X[i, :]#迭代次数增加t += 1#记录当前错误error_now = count(X, y, w)if error_now < error:error = error_noww0 = np.copy(w)#移动到下一个元素i += 1#如果达到n,则重置为0if i == n:i = 0return error, w0#运行g算法n次,1代表训练集,2代表测试集
def average_of_n(g, X1, y1, X2, y2, n, eta=1, max_step=np.inf):result = []data = np.c_[X1, y1]m = X2.shape[0]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]w = g(X, y, eta=eta, max_step=max_step)[-1]result.append(count(X2, y2, w) / m)plt.hist(result)plt.xlabel("错误率")plt.title("平均错误率为"+str(np.mean(result)))plt.show()
主函数:
import matplotlib.pyplot as plt
import numpy as np
import utils as util
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号data_train = np.genfromtxt("hw1_18_train.dat")
data_test = np.genfromtxt("hw1_18_test.dat")X_train, y_train = util.preprocess(data_train)
X_test, y_test = util.preprocess(data_test)util.average_of_n(util.Pocket_PLA, X_train, y_train, X_test, y_test, 2000, max_step=100)
相关文章:

ccc-台大林轩田机器学习基石-hw1
文章目录Question1-14Question15-PLAQuestion16-PLA平均迭代次数Question17-不同迭代系数的PLAQuestion18-Pocket_PLAQuestion19-PLA的错误率Question20-修改Pocket_PLA迭代次数Question1-14 对于有明确公式和定义的不需要使用到ml 智能系统在与环境的连续互动中学习最优行为策…...

hadoop03-MapReduce【尚硅谷】
大数据学习笔记 MapReduce 一、MapReduce概述 MapReduce是一个分布式运算程序的编程框架,是基于Hadoop的数据分析计算的核心框架。 MapReduce处理过程为两个阶段:Map和Reduce。 Map负责把一个任务分解成多个任务;Reduce负责把分解后多任务处…...

测牛学堂:软件测试python学习之异常处理
python的捕获异常 程序在运行时,如果python解释器遇到一个错误,则会停止程序的执行,并且提示一些错误信息,这就是异常。 程序停止执行并且提示错误信息,称之为抛出异常。 因为程序遇到错误会停止执行,有时…...

图神经网络--图神经网络
图神经网络 图神经网络图神经网络一、PageRank简介1.1互联网的图表示1.2PageRank算法概述1.3求解PageRank二、代码实战2.1引入库2.2加载数据,并构建图2.3计算每个节点PageRank重要度2.4用节点尺寸可视化PageRank值一、PageRank简介 PageRank是Google最早的搜索引擎…...

React useCallback如何使其性能最大化?
前言 React中最让人畅谈的就是其带来的灵活性,可以说写起来非常的舒服。但是也就是它的灵活性太强,往往让我们忽略了很多细节的地方,而就是这些细节的东西能进行优化,减小我们的性能开销。可以说刚学React和工作几年后写React的代…...
长尾关键词使用方法,通过什么方式挖掘长尾关键词?
当你在搜索引擎的搜索栏中输入有关如何使用长尾关键词的查询时,你可能希望有简单快捷的方式出现在搜索结果中,可以帮助你更好地应用seo。 不过,这里要记住一件事:SEO 策略只会为你的网站带来流量;在你的产品良好之前&a…...

【网络编程套接字(一)】
网络编程套接字(一)理解源IP地址和目的IP地址理解源MAC地址和目的MAC地址理解源端口号和目的端口号PORT VS PID认识TCP协议和UDP协议网络字节序socket编程接口socket常见APIsockaddr结构简单的UDP网络程序服务端创建套接字服务端绑定字符串IP VS 整数IP客…...
shell脚本入门
实习的时候第一个月的考核就是如何部署一个云资源,当时走的捷径(杠杠的搜索能力hhhh)找到了一个shell脚本一键部署,后来被leader问起来就如实说了,leader问有没有看懂shell脚本中的逻辑……(没有࿰…...
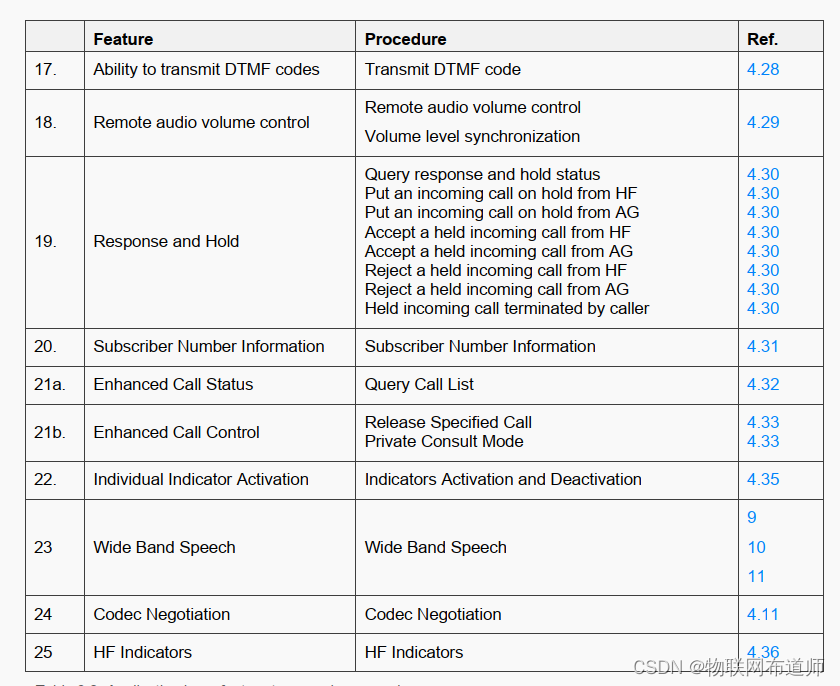
【经典蓝牙】 蓝牙HFP层协议分析
HFP 概述 HFP概念介绍 HFP(Hands-Free Profile), 是蓝牙免提协议, 可以让蓝牙设备对对端蓝牙设备的通话进行控制,例如蓝牙耳机控制手机通话的接听、 挂断、 拒接、 语音拨号等。HFP中蓝牙两端的数据交互是通过定义好的AT指令来通讯的。 &am…...
)
互联网摸鱼日报(2023-02-26)
互联网摸鱼日报(2023-02-26) InfoQ 热门话题 迁移工具 Air2phin 宣布开源,2 步迁移 Airflow 至 Dolphinscheduler 专访奇安信董国伟博士:目前开源安全的现状并不乐观,但其重要性已成各方共识 专访Brian Behlendorf&…...

关于程序员中年危机的一个真实案例
关于中年危机,网上已经有了各种各样的解读。但是,这两天一个学员跟我简单几句聊天,却触发了对于中年危机的另一种思考。如果你曾经也有点迷茫,或许你可以稍微花几分钟看下这个故事。 一、无奈的故事 39岁还出来面试&#x…...
【fly-iot飞凡物联】(2):如何从0打造自己的物联网平台,使用开源的技术栈搭建一个高性能的物联网平台,目前在设计阶段。
目录前言1,fly-iot 飞凡物联2,mqtt-broker 服务3, 管理后台产品/设备设计4,数据存储目前使用mysql,消息存储到influxdb中5,规则引擎使用 ekuiper6, 总结和其他的想法前言 本文的原文连接是: https://blog.csdn.net/freewebsys/article/detail…...
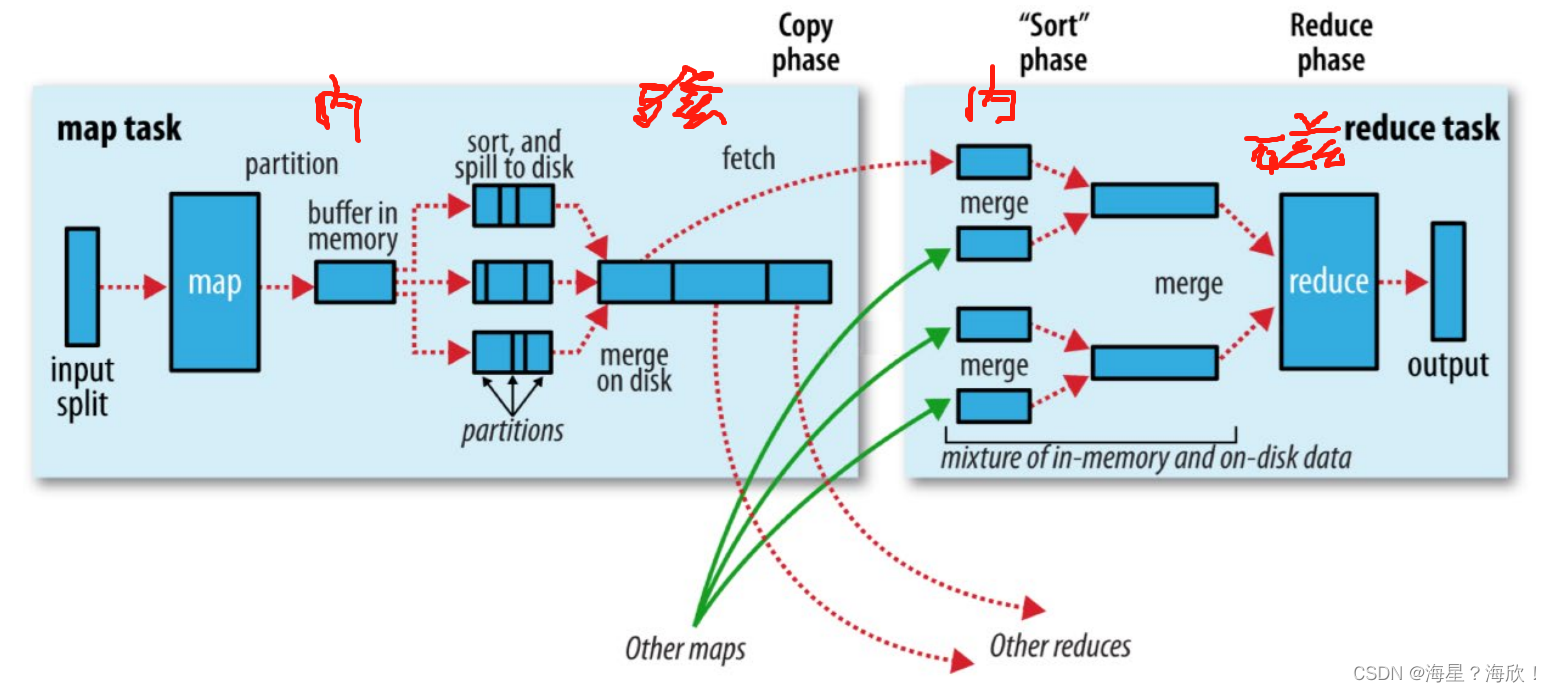
Hadoop MapReduce
目录1.1 MapReduce介绍1.2 MapReduce优缺点MapReduce实例进程阶段组成1.3 Hadoop MapReduce官方示例案例:评估圆周率π(PI)的值案例:wordcount单词词频统计1.4 Map阶段执行流程1.5 Reduce阶段执行流程1.6 Shuffle机制1.1 MapReduc…...
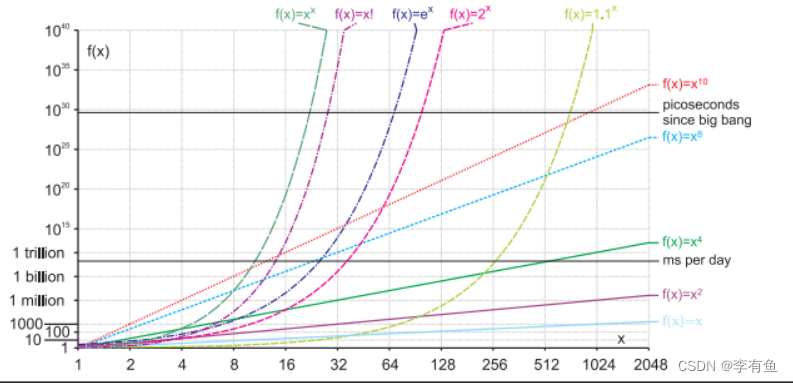
时间复杂度和空间复杂度详解
有一堆数据需要排序,A要使用快速排序,B要使用堆排序,A认为自己的代码更高效,B也认为自己的代码更高效,在这种情况下,怎么来判断谁的代码更好一点呢?这时候就有了时间复杂度和空间复杂度。 目录 …...

【C++】面向对象---封装
【C】面向对象—封装 1.封装的意义 封装是C面向对象三大特性之一 封装的意义: 将属性和行为作为一个整体,表现生活的事物将属性和行为加以权限控制 封装意义一: 在设计类的时候,属性和行为写在一起,表现事物 语…...

Docker简介
一、介绍容器虚拟化技术(带环境安装的一种解决方案)打破程序即应用的观念,透过镜像image将作业系统核心除外,运用应用程序所需要的运行环境,由上而下打包,达到应用程序跨平台间的无缝接轨运作。Docker是基于…...
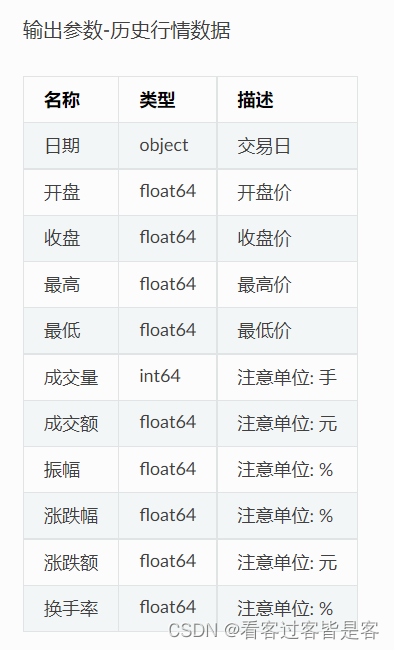
量化学习(一)数据获取
试验环境 windows10 AnacondaPyCharm(小白参考文章:https://coderx.com.cn/?p14) VM中安装MySQL5.7(设置utf8及相应配置优化) 关于复权 小白参考文章:https://zhuanlan.zhihu.com/p/469820288 数据来源 AK…...

java并发编程讨论:锁的选择
java并发编程 线程堆栈大小 单线程的堆栈大小默认为1M,1000个线程内存就占了1G。所以,受制于内存上限,单纯依靠多线程难以支持大量任务并发。 上下文切换开销 ReentrantLock 2个线程交替自增一个共享变量,使用ReentrantLock&…...

大数据框架之Hadoop:MapReduce(三)MapReduce框架原理——ReduceTask工作机制
1、ReduceTask工作机制 ReduceTask工作机制,如下图所示。 (1)Copy阶段:ReduceTask从各个MapTask上远程拷贝一片数据,并针对某一片数据,如果其大小超过一定阈值,则写到磁盘上,否则直…...

Nginx的介绍、安装与常用命令
前言:传统结构上(如下图所示)我们只会部署一台服务器用来跑服务,在并发量小,用户访问少的情况下基本够用但随着用户访问的越来越多,并发量慢慢增多了,这时候一台服务器已经不能满足我们了,需要我们增加服务…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
