算法设计与分析第二章作业
1. 描述最大字段和的分治算法
题目

思路
判断最大子段和,可以用分治的思想,每次将序列一分为二,选择两个序列的最大子段和。
但是这里还有一种可能,就是子段可以横跨两个子序列,所以我们的最大子段和就是:
MAX(左边序列最大字段和,横跨两序列的最大子段和,右边序列的最大子段和)。
对于左右两边的最大子段和,可以用分治递归的方法来做,临界条件就是序列中只剩一个数了,这时候最大子段和就是这个数,而递归函数就是对左右两边分别求最大子段和(调用自身),而且还得求跨序列的最大子段和,取三者的最大值来返回。
那么怎么求跨序列的最大子段和呢?其实很简单,首先要对原来的大序列添加几个指针,开头的是指针l,最右边的是指针r,因为要分治,所以再设置一个中间的指针mid,此时序列就可以分为两个部分,分别是(l,mid)和(mid+1,r),这时候的跨序列子段,必须包含mid和mid+1这两个地方,当然也可以向左或向右延申,所以,我们只需要求出从mid开始向左延申的最大字段和,还有从mid+1开始向右延申的最大子段和,将两者相加,就能得到跨序列的最大子段和了。
思路很好理解,照着上面的描述画出图来就一目了然了。下面来看看代码实现吧。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5;
int n, a[N];
int maxSum (int left, int right) {if (left == right)return a[left];int mid = left + right >> 1;int lmax = maxSum (left, mid);int rmax = maxSum (mid + 1, right);int sum = a[mid];int clmax = a[mid];for (int i = mid - 1; i >= left; i--) {sum += a[i];if (sum > clmax)clmax = sum;}sum = a[mid + 1];int crmax = a[mid + 1];for (int i = mid + 2; i <= right; i++) {sum += a[i];if (sum > crmax)crmax = sum;}int cmax = clmax + crmax;int maxsum = max (cmax, max (lmax, rmax));if (maxsum < 0)maxsum = 0;return maxsum;
}
int main () {cin >> n;for (int i = 0; i < n; i++)cin >> a[i];cout << maxSum (0, n - 1);return 0;
}
2. 分析该算法的时间复杂度
分解子问题:O(1)
求解子问题:2T(n/2)
合并子问题:O(n)
故时间复杂度为T(n)=2T(n/2)+O(n)=nlogn
3. 对分治法的体会和思考
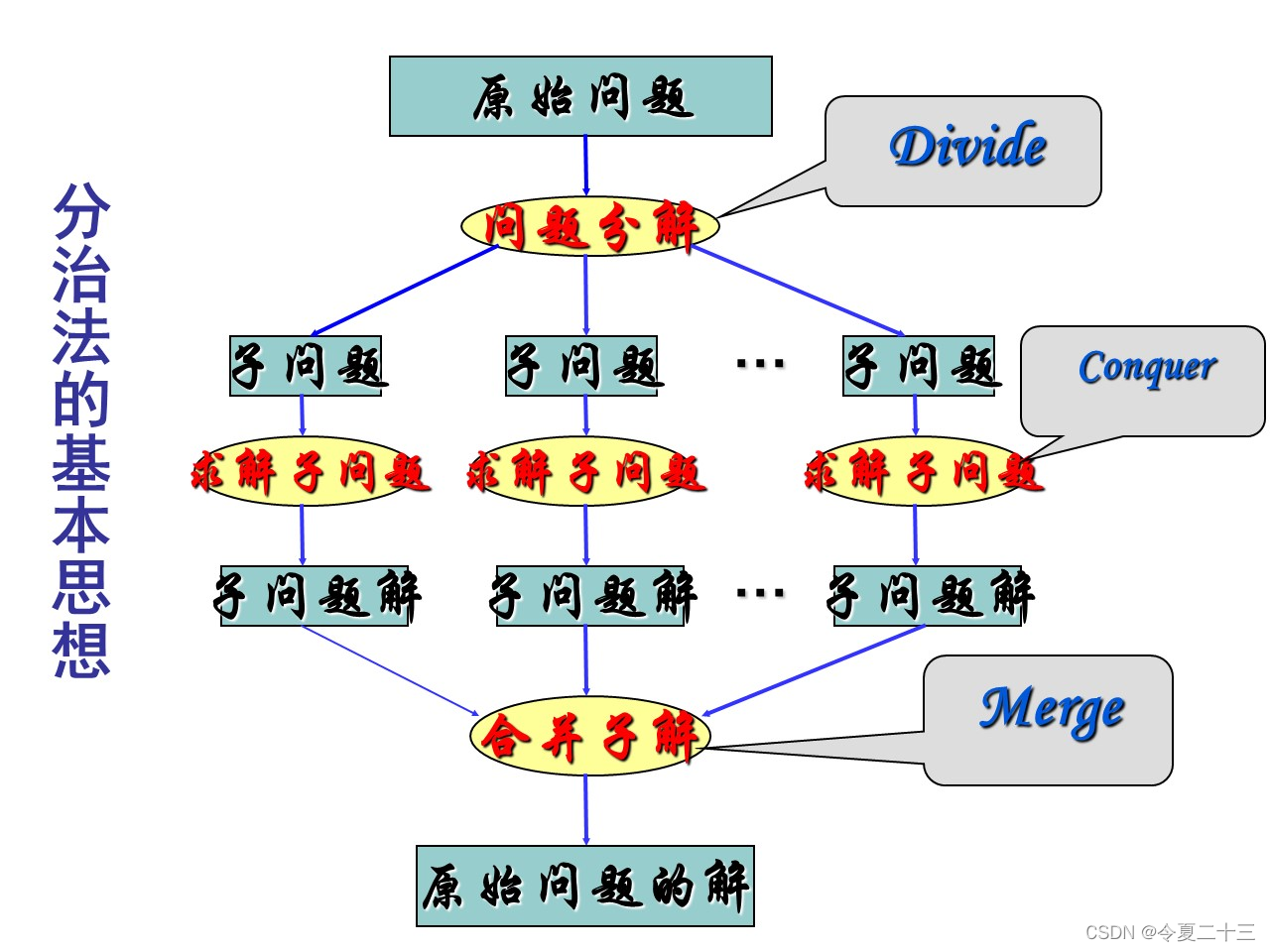
分治法的设计思想是,将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
其中的划分再击破,和递归的分解再解决异曲同工,其实同样用到了递归的思想,只不过分治法先分再治,最后还得合并。
相关文章:

算法设计与分析第二章作业
1. 描述最大字段和的分治算法 题目 思路 判断最大子段和,可以用分治的思想,每次将序列一分为二,选择两个序列的最大子段和。 但是这里还有一种可能,就是子段可以横跨两个子序列,所以我们的最大子段和就是࿱…...

《视觉SLAM十四讲》-- 三维空间的刚体运动
文章目录 02 三维空间的刚体运动2.0 机器人位姿表述2.1 点和坐标系2.1.1 三维坐标系有关表述2.1.2 坐标系变换 2.2 旋转向量和欧拉角2.2.1 旋转向量2.2.2 欧拉角 2.3 四元数2.3.1 四元数的定义2.3.2 四元数的计算2.3.3 四元数表示旋转2.3.4 四元数与其他旋转表示法的转换 2.4 相…...

关于iOS:如何使用SwiftUI调整图片大小?
How to resize Image with SwiftUI? 我在Assets.xcassets中拥有很大的形象。 如何使用SwiftUI调整图像大小以缩小图像? 我试图设置框架,但不起作用: 1 2 Image(room.thumbnailImage) .frame(width: 32.0, height: 32.0) 在Image上应用…...

【MySQL】数据库MySQL基础知识与操作
作者主页:paper jie_博客 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文录入于《MySQL》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精力)打造&a…...
)
vim手册(vim cheatsheet)
vim手册(vim cheatsheet) 1. 命令模式 1). 移动光标 在命令模式下,可以使用以下命令来移动光标: - h:向左移动一个字符。 - j:向下移动一行。 - k:向上移动一行。 - l:向右移动一个…...
软件测试具体人员分工
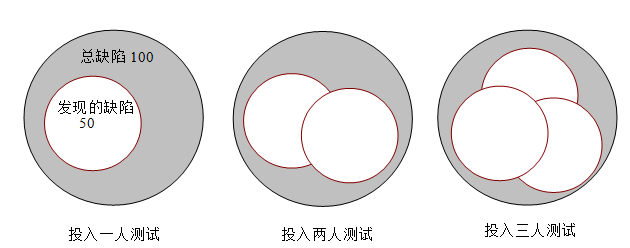
最近看了点敏捷测试的东西,看得比较模糊。一方面是因为没有见真实的环境与流程,也许它跟本就没有固定的模式与流程,它就像告诉人们要“勇敢”“努力”。有的人在勇敢的面对生活,有些人在勇敢的挑战自我,有些人在勇敢的…...
计算机网络-应用层
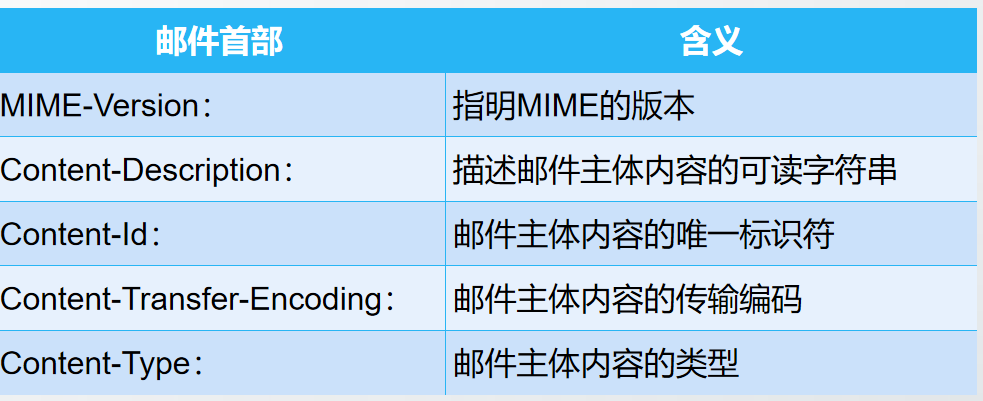
文章目录 应用层协议原理万维网和HTTP协议万维网概述统一资源定位符HTML文档 超文本传输协议(HTTP)HTTP报文格式请求报文响应报文cookie 万维网缓存与代理服务器 DNS系统域名空间域名服务器和资源记录域名解析过程递归查询迭代查询 动态主机配置协议&…...
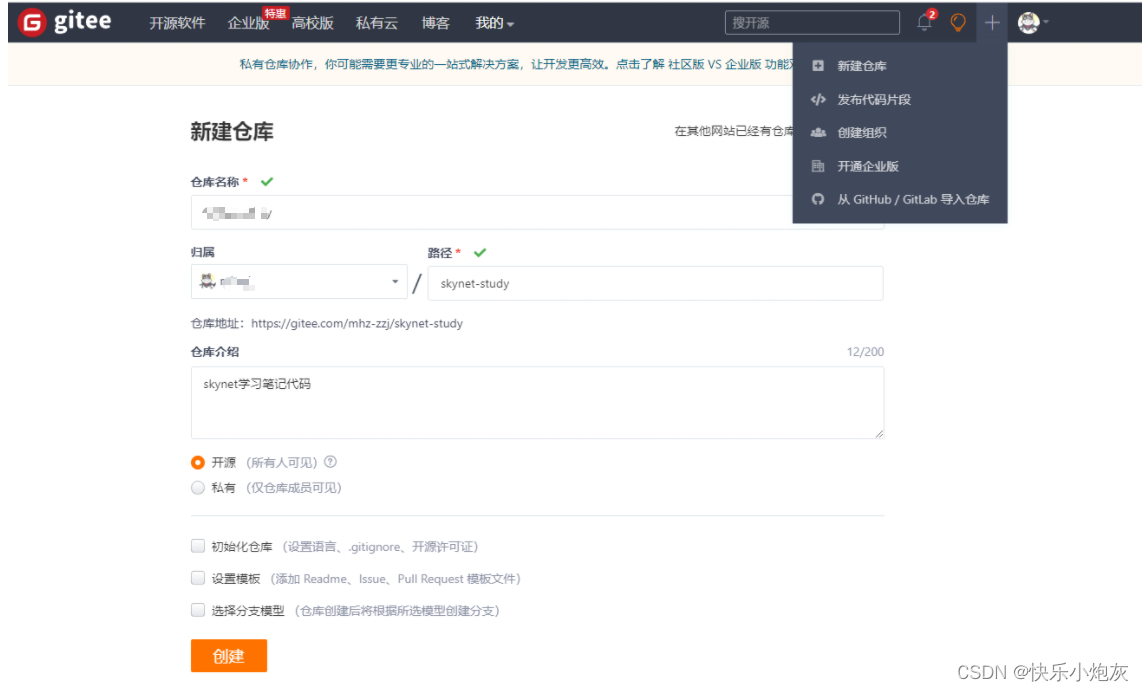
linux 创建git项目并提交到gitee(保姆式教程)
01、git安装与初始化设置 mhzzjmhzzj-virtual-machine:~/work/skynetStudy$ apt install mhzzjmhzzj-virtual-machine:~/work/skynetStudy$ git config --global user.name "用户名" mhzzjmhzzj-virtual-machine:~/work/skynetStudy$ git config --global user.ema…...

STM32 IAP应用开发--bootloader升级程序
STM32 IAP应用开发--bootloader升级程序 Chapter1 STM32 IAP应用开发——通过串口/RS485实现固件升级(方式2)前言什么是IAP?什么是BootLoader? 方案介绍:1)bootloader部分:2)APP部分…...

Q_GLOBAL_STATIC宏
文章目录 目的Q_GLOBAL_STATIC源代码分析涉及到原子操作 以及静态变量初始化顺序代码实现 目的 由Q_GLOBAL_STATIC宏, 引发的基于线程安全的Qt 单例模式的使用。 Q_GLOBAL_STATIC /***************************************************************************…...

[批处理]_[初级]_[如何删除变量值里的双引号]
场景 在使用Visual Studio开发本地程序的时,需要在项目属性,生成事件->生成后事件里增加一些资源的打包,复制,删除等操作,那么就需要用到批处理来进行。而传递带空格的路径给外部的批处理文件时就需要双引号引用从…...
51单片机电子钟闹钟温度LCD1602液晶显示设计( proteus仿真+程序+原理图+设计报告+讲解视频)
51单片机电子钟闹钟温度液晶显示设计( proteus仿真程序原理图设计报告讲解视频) 1.主要功能:2.仿真3. 程序代码4. 原理图5. 设计报告6. 设计资料内容清单&&下载链接资料下载链接(可点击): 🌟51单片…...

怎样学好java
最近在看一本java方面的书。《java从入门到精通》,里面看到一段如何学习java的话,觉得非常好,下面我分享一下。 如何学好java语言,是所有初学者都需要面对的问题。其实,每种语言的学习方法都大同小异。初学者需要注意…...

HarmonyOS 数据管理与应用数据持久化(二)
通过键值型数据库实现数据持久化 场景介绍 键值型数据库存储键值对形式的数据,当需要存储的数据没有复杂的关系模型,比如存储商品名称及对应价格、员工工号及今日是否已出勤等,由于数据复杂度低,更容易兼容不同数据库版本和设备…...
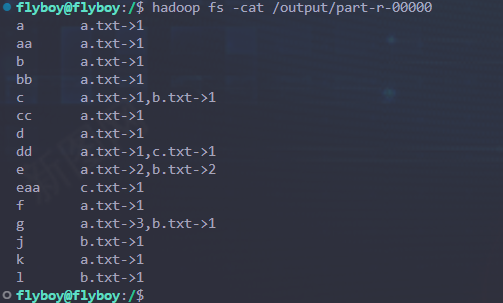
Hadoop环境搭建及Demo
参考博客 Windows 10安装Hadoop 3.3.0教程 (kontext.tech) Hadoop入门篇——伪分布模式安装 & WordCount词频统计 | Liu Baoshuai’s Blog Hadoop安装教程 Linux版_linux和hadoop的安装_lnlnldczxy的博客-CSDN博客 hadoop启动出错 The value of property bind.address …...
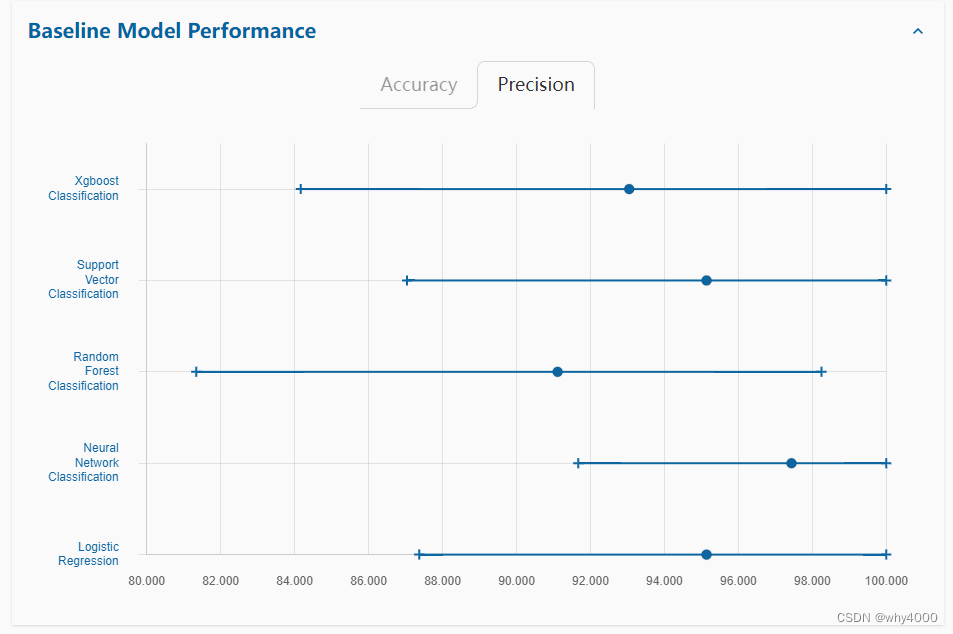
更新一下数据集
UCI Machine Learning Repository UCI的数据集还是挺老牌的,最近换了地址,我就再记录一下。 左边是比较常见的数据集,比如Iris很经典,Heart Disease这也是,包括Wine,通常对于初学者学习比较好,…...

web3之跨链预言机SupraOracles:什么是Supra
文章目录 web3之跨链预言机SupraOracles什么是Supra什么是DORA(分布式Oracle协议)使用场景web3之跨链预言机SupraOracles 什么是Supra 官网:https://supraoracles.com/ 预言机的核心价值就在于数据传输,数据传输的速度、准确性、安全性更是重中之重。Supra Oracles 就是这…...

关系型数据库 期末复习(未完
关系型数据库 绪论概念间的关系数据库的历史信息和数据数据模型 关系模型数据结构关系完整性关系操作语言 关系代数语言 绪论 概念间的关系 数据->数据库->数据库管理系统->数据库系统 数据库的历史 人工管理阶段 -> 文件系统阶段 -> 数据库系统阶段 数据库…...

【学习笔记】CF1895G Two Characters, Two Colors
感谢grass8sheep提供的思路。 首先,我们可以用 D P DP DP解决这个问题。 设 f i , j f_{i,j} fi,j表示前 i i i个数中有 j j j个为 1 1 1的位置为红色的最大价值。则转移如下: f i , j ← f i − 1 , j b i f_{i,j}\gets f_{i-1,j}b_i fi,j←fi−…...
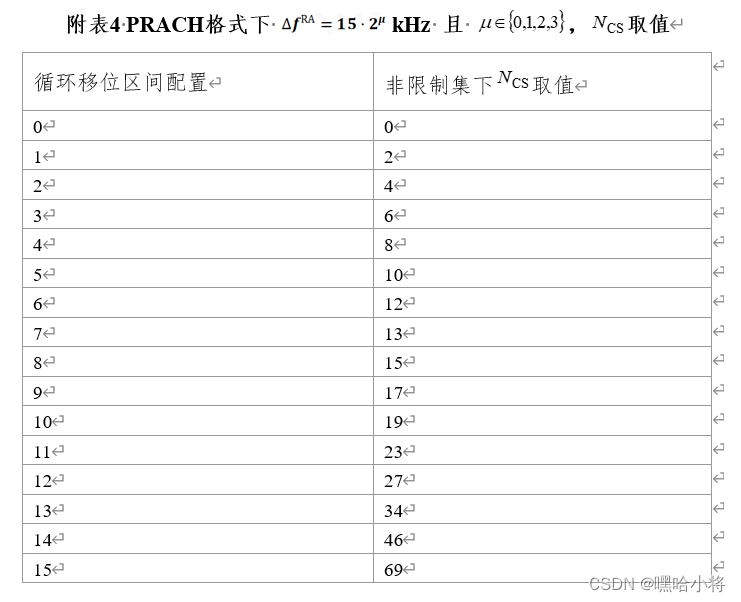
GZ035 5G组网与运维赛题第10套
2023年全国职业院校技能大赛 GZ035 5G组网与运维赛项(高职组) 赛题第10套 一、竞赛须知 1.竞赛内容分布 竞赛模块1--5G公共网络规划部署与开通(35分) 子任务1:5G公共网络部署与调试(15分) 子…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
