0-1背包、完全背包及其变形【零神基础精讲】
来源0x3f:https://space.bilibili.com/206214
三叶姐的对背包问题的总结:【宫水三叶】详解完全背包一维空间优化推导(附背包问题攻略)https://leetcode.cn/circle/discuss/GWpXCM/
文章目录
- 0-1背包、完全背包及其拓展(选/不选思想的代表)
- 0-1背包常见变形【至多/恰好/至少】 :※重要
- 纯0-1背包问题
- [494. 目标和](https://leetcode.cn/problems/target-sum/)
- 记忆化搜索
- 1:1翻译成递推(动态规划)
- 空间优化:滚动数组
- 空间优化(一个数组)从后往前遍历背包
- 完全背包变形
- 纯完全背包问题
- [322. 零钱兑换](https://leetcode.cn/problems/coin-change/)
- 记忆化搜索
- 翻译成递推
- 空间优化(一维数组)从前到后遍历背包
- 练习
- [416. 分割等和子集](https://leetcode.cn/problems/partition-equal-subset-sum/)
- [279. 完全平方数](https://leetcode.cn/problems/perfect-squares/)
- [518. 零钱兑换 II](https://leetcode.cn/problems/coin-change-ii/)
对边界条件的总结:
不同的题目,所要的答案不同, 比如:方案数,最大、小值,数字个数,能否构成?
这也就意味着 dp 数组值可以为数值,也可以是 boolean 类型
另外,同样是数值的情况下,不同的要求,也会造成不同的初始值 f【0】【0】:
-
能否构成: f【0】【0】 = True ; 0 可以构成 0
-
方案数: f【0】【0】 = 1 ; 0 组成 0 只有一种方案
-
数字个数: f【0】【0】 = 0 ; 0 组成 0 没有使用数字
-
最大、小值: 问题一般会回归到 方案数 或 数字个数问题, 一般会使用到 max/min 函数约束答案,而且会使用 ±inf 初始化来表示极端情况。 比如:力扣 279 求最小数量(f【0】【j】 的初始值也是要考虑的)
0-1背包、完全背包及其拓展(选/不选思想的代表)
0-1背包常见变形【至多/恰好/至少】 :※重要
1、至多装capacity,求方案数/最大价值和
2、恰好装capacity,求方案数/最大/最小价值和
3、至少装capacity,求方案数/最小价值和
纯0-1背包问题
0-1背包问题:有N件物品和一个容量为C的背包。第i件物品的费用是v[i],价值是w[i]。
求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
dp[N][C+1]解法
import java.util.Scanner;
public class Main{ public static void main(String[] args){ Scanner sc = new Scanner(System.in); int N = sc.nextInt(); int C = sc.nextInt(); int[] v = new int[N]; int[] w = new int[N]; for (int i = 0; i < N; i++){ v[i] = sc.nextInt(); w[i] = sc.nextInt(); }System.out.println(maxValue(N, C, v, w)); }private static int maxValue(int N, int C, int[] v, int[] w) {int[][] dp = new int[N][C + 1];dp[0][0] = 0;//填充第 0 位物品在 0-C 容量下的初始值for (int i = 0; i < C + 1; i++) {dp[0][i] = i >= v[0] ? w[0] : 0;}// 先遍历物品 再遍历背包for (int i = 1; i < N; i++) {for (int j = 0; j < C + 1; j++) {int n = dp[i - 1][j]; // 不选该物品int y = 0;if (j >= v[i]) {y = w[i] + dp[i - 1][j - v[i]]; // 选择该物品}dp[i][j] = Math.max(n, y);}}return dp[N - 1][C];}
}
dp[2][C+1]解法
private static int maxValue(int N, int C, int[] v, int[] w) {int[][] dp = new int[2][C + 1];dp[0][0] = 0;for (int i = 0; i < C + 1; i++) {dp[0][i] = i >= v[0] ? w[0] : 0;}for (int i = 1; i < N; i++) {for (int j = 0; j < C + 1; j++) {int n = dp[(i - 1)%2][j]; // 不选该物品int y = 0;if (j >= v[i]) {y = w[i] + dp[(i - 1)%2][j - v[i]]; // 选择该物品}dp[i%2][j] = Math.max(n, y);}}return dp[(N - 1)%2][C];}
dp[C+1]解法
private static int maxValue(int N, int C, int[] v, int[] w) {int[] dp = new int[C + 1];for (int i = 0; i < C + 1; i++) {dp[i] = i >= v[0] ? w[0] : 0;}for (int i = 1; i < N; i++) {for (int j = C; j >= 0; j--) {int n = dp[j]; // 不选该物品int y = 0;if (j >= v[i]) {y = w[i] + dp[j - v[i]]; // 选择该物品}dp[j] = Math.max(n, y);}}return dp[C];}
494. 目标和
难度中等1515
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
从什么都不知道的题目到0-1背包问题的推理过程:
设添加+号的数和为p
则添加 - 号的数和为 sum-p
则 p-(sum-p) = target
==> p = (s+t)/2 => 在nums中选择一些数字,使得和恰好为p
记忆化搜索
class Solution {int[] nums;int[][] cache;public int findTargetSumWays(int[] nums, int target) {for(int x : nums) target += x;if(target < 0 || target % 2 == 1) return 0;target /= 2;this.nums = nums;int n = nums.length;cache = new int[n][target+1];for (int i = 0; i < n; i++)Arrays.fill(cache[i], -1); // -1 表示没用访问过return dfs(n - 1, target);}public int dfs(int i, int c){if(i < 0) return c == 0 ? 1 : 0;if(cache[i][c] != -1) return cache[i][c];int res = 0;if(c < nums[i]) {res = dfs(i-1, c); // 没有容量装下i位置的物体了}else{res = dfs(i-1, c) + dfs(i-1, c - nums[i]);}cache[i][c] = res;return res;}
}
1:1翻译成递推(动态规划)
class Solution {int[] nums;int[][] cache;public int findTargetSumWays(int[] nums, int target) {for(int x : nums) target += x;if(target < 0 || target % 2 == 1) return 0;target /= 2;int n = nums.length;int[][] f = new int[n+1][target+1];f[0][0] = 1; // 容量未0,所有数都选了for(int i = 0; i < n; i++){for(int c = 0; c <= target; c++){if(c < nums[i]){f[i+1][c] = f[i][c];}else{f[i+1][c] = f[i][c] + f[i][c-nums[i]];}}}return f[n][target];}// public int dfs(int i, int c){// if(i < 0) return c == 0 ? 1 : 0;// if(cache[i][c] != -1) return cache[i][c];// int res = 0;// if(c < nums[i]) {// res = dfs(i-1, c); // 没有容量装下i位置的物体了// }else{// res = dfs(i-1, c) + dfs(i-1, c - nums[i]);// }// cache[i][c] = res;// return res;// }
}
空间优化:滚动数组
(i+1) ==> (i+1) % 2
class Solution {int[] nums;int[][] cache;public int findTargetSumWays(int[] nums, int target) {for(int x : nums) target += x;if(target < 0 || target % 2 == 1) return 0;target /= 2;int n = nums.length;int[][] f = new int[2][target+1];f[0][0] = 1; // 容量未0,所有数都选了for(int i = 0; i < n; i++){for(int c = 0; c <= target; c++){if(c < nums[i]){f[(i+1) % 2][c] = f[i % 2][c];}else{f[(i+1) % 2][c] = f[i % 2][c] + f[i % 2][c-nums[i]];}}}return f[n % 2][target];}
}
空间优化(一个数组)从后往前遍历背包
从后往前遍历容量c
class Solution {int[] nums;int[][] cache;public int findTargetSumWays(int[] nums, int target) {for(int x : nums) target += x;if(target < 0 || target % 2 == 1) return 0;target /= 2;int n = nums.length;int[] f = new int[target+1];f[0] = 1; // 容量未0,所有数都选了for(int i = 0; i < n; i++){for(int c = target; c >= nums[i]; c--){f[c] = f[c] + f[c-nums[i]];}}return f[target];}
}
完全背包变形
纯完全背包问题
完全背包问题 : 有 N 种物品和一个容量为 C 的背包,每种物品都有无限件。
第 i 件物品的体积是 v[i],价值是 w[i]。
求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
其实就是在 0-1 背包问题的基础上,增加了每件物品可以选择多次的特点(在容量允许的情况下)。
import java.util.Scanner;
public class Main{ public static void main(String[] args){ Scanner sc = new Scanner(System.in); int N = sc.nextInt(); int C = sc.nextInt(); int[] v = new int[N]; int[] w = new int[N]; for (int i = 0; i < N; i++){ v[i] = sc.nextInt(); w[i] = sc.nextInt(); }System.out.println(maxValue(N, C, v, w)); }private static int maxValue(int N, int C, int[] v, int[] w) {int[] dp = new int[C + 1];//先遍历物品,再遍历背包for (int i = 0; i < N; i++) {for (int j = C; j >= v[i]; j--) {//比较格子的数量等于最多可选第i件物品多少次for (int k = 0 ;; k++) {if (j < v[i] * k) {break;}dp[j] = Math.max(dp[j], dp[j - v[i] * k] + w[i] * k);}}}return dp[C];}
}
完全背包的dp[C+1]解法
private static int maxValue(int N, int C, int[] v, int[] w) {int[] dp = new int[C + 1];for (int i = 0; i < N; i++) {// for (int j = C; j >= v[i]; j--) { // 0-1 背包问题for (int j = v[i]; j <= C; j++) { // 完全背包问题int n = dp[j]; // 不选该物品int y = w[i] + dp[j - v[i]]; // 选择该物品dp[j] = Math.max(n, y);}}return dp[C];}
}322. 零钱兑换
难度中等2307
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
记忆化搜索
class Solution {private int[] coins;private int[][] cache;public int coinChange(int[] coins, int amount) {this.coins = coins;int n = coins.length;cache = new int[n][amount + 1];for (int i = 0; i < n; i++)Arrays.fill(cache[i], -1); // -1 表示没用访问过int ans = dfs(n - 1, amount);return ans < Integer.MAX_VALUE / 2 ? ans : -1;}private int dfs(int i, int c) {// 当 c==0 时,表示这是一个合法的方案if (i < 0) return c == 0 ? 0 : Integer.MAX_VALUE / 2; // 除 2 是防止下面 + 1 溢出if (cache[i][c] != -1) return cache[i][c];if (c < coins[i]) return cache[i][c] = dfs(i - 1, c);return cache[i][c] = Math.min(dfs(i - 1, c), dfs(i, c - coins[i]) + 1);}
}
翻译成递推
class Solution {public int coinChange(int[] coins, int amount) {int n = coins.length;int[][] f = new int[n + 1][amount + 1];Arrays.fill(f[0], Integer.MAX_VALUE / 2); // 除 2 是防止下面 + 1 溢出f[0][0] = 0;for (int i = 0; i < n; ++i)for (int c = 0; c <= amount; ++c)if (c < coins[i]) f[i + 1][c] = f[i][c];else f[i + 1][c] = Math.min(f[i][c], f[i + 1][c - coins[i]] + 1);int ans = f[n][amount];return ans < Integer.MAX_VALUE / 2 ? ans : -1;}
}
空间优化(一维数组)从前到后遍历背包
class Solution {public int coinChange(int[] coins, int amount) {int[] f = new int[amount + 1];Arrays.fill(f, Integer.MAX_VALUE / 2); // 除 2 是防止下面 + 1 溢出f[0] = 0;for (int x : coins)for (int c = x; c <= amount; ++c)f[c] = Math.min(f[c], f[c - x] + 1);int ans = f[amount];return ans < Integer.MAX_VALUE / 2 ? ans : -1;}
}
练习
416. 分割等和子集
难度中等1645
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 2001 <= nums[i] <= 100
class Solution {// 每个元素只可以取一次,元素的价值和大小就是自己本身public boolean canPartition(int[] nums) {Arrays.sort(nums);int sum = 0;for(int num : nums) sum += num;if(sum % 2 != 0) return false;int target = sum / 2; // 背包为target时,有没有价值和为target(价值和只可能 <= target)int[] dp = new int[target+1]; // 空间优化:一个数组for(int i = 0; i < nums.length; i++){for(int j = target; j >= nums[i]; j--){dp[j] = Math.max(dp[j], dp[j-nums[i]] + nums[i]);}}return dp[target] == target ? true : false;}
}
279. 完全平方数
难度中等1619
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
提示:
1 <= n <= 104
朴素完全背包解法
class Solution {private static final int INF = Integer.MAX_VALUE / 2;public int numSquares(int n) {// 将可能用到的【物品】预处理出来List<Integer> list = new ArrayList<>();for(int i = 1; i * i <= n; i++) list.add(i*i);// 问题就变成了:给定数字中,每个数字可以使用无限次,求凑出目标值n所需要的最少数字个数是多少int[][] dp = new int[list.size()+1][n+1]; // 前i个数字中,凑出数字总和j所需要的最少数字个数//当没有任何数时,除了 f[0][0] 为 0(花费 0 个数值凑出 0),其他均为无效值Arrays.fill(dp[0], INF); dp[0][0] = 0;// dp[i][j] = min(dp[i-1][j-k*t]+k) 0 <= k*t <= j; k:选k个数字i,第i个数字数值为tfor(int i = 1; i <= list.size(); i++){int x = list.get(i-1);for(int j = 0; j <= n; j++){// 对于不选第 i 个数的情况dp[i][j] = dp[i-1][j];// 对于选 k 次第 i 个数的情况for(int k = 1; k * x <= j; k++){// 能够选择 k 个 x 的前提是剩余的数字 j - k * x 也能被凑出if(dp[i-1][j-k*x] != INF){dp[i][j] = Math.min(dp[i][j], dp[i-1][j-k*x] + k);}}}}return dp[list.size()][n];}
}
空间优化:
class Solution {private static final int INF = Integer.MAX_VALUE / 2;public int numSquares(int n) {// 将可能用到的【物品】预处理出来List<Integer> list = new ArrayList<>();for(int i = 1; i * i <= n; i++) list.add(i*i);// 问题就变成了:给定数字中,每个数字可以使用无限次,求凑出目标值n所需要的最少数字个数是多少int[] dp = new int[n+1]; // 前i个数字中,凑出数字总和j所需要的最少数字个数//当没有任何数时,除了 f[0][0] 为 0(花费 0 个数值凑出 0),其他均为无效值Arrays.fill(dp, INF); dp[0] = 0;// dp[i][j] = min(dp[i-1][j-k*t]+k) 0 <= k*t <= j; k:选k个数字i,第i个数字数值为tfor(int i = 1; i <= list.size(); i++){int x = list.get(i-1);for(int j = x; j <= n; j++){dp[j] = Math.min(dp[j], dp[j-x] + 1);}}return dp[n];}
}
518. 零钱兑换 II
难度中等1005
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入:amount = 3, coins = [2]
输出:0
解释:只用面额 2 的硬币不能凑成总金额 3 。
示例 3:
输入:amount = 10, coins = [10]
输出:1
提示:
1 <= coins.length <= 3001 <= coins[i] <= 5000coins中的所有值 互不相同0 <= amount <= 5000
class Solution {public int change(int amount, int[] coins) {int[] dp = new int[amount+1];dp[0] = 1;for(int x : coins){for(int j = x; j <= amount; j++){dp[j] = dp[j] + dp[j-x];}}return dp[amount];}
}
相关文章:

0-1背包、完全背包及其变形【零神基础精讲】
来源0x3f:https://space.bilibili.com/206214 三叶姐的对背包问题的总结:【宫水三叶】详解完全背包一维空间优化推导(附背包问题攻略)https://leetcode.cn/circle/discuss/GWpXCM/ 文章目录0-1背包、完全背包及其拓展(…...

OpenStack
OpenStack优势: 1、模块松耦合。 2、组件配置较为灵活。 3、二次开发容易 OpenStack共享服务组件: 1、数据库服务:MongoDB 2、消息列队:RabbitMQ 3、缓存:Redis 4、存储:Ceph 5、负载均衡ÿ…...
Spring Boot整合Kaptcha实现验证码功能
目录一、前言1.Kaptcha 简介2.Kaptcha 详细配置表二、实现1.整合kaptcha,创建kaptcha的工具类1.1 添加依赖1.2 创建KaptchaConfig工具类2 编写接口,在接口中使用 kaptcha 工具类来生成验证码图片(验证码信息)并返回3 登录时从sess…...

【2023】某python语言程序设计跟学第一周内容
本文说明: 案例内容为北理工python语言程序设计课程,如有不妥请联系! 目录温度转换案例:执行结果:代码解析:白话说明:举一反三:根据输入半径求圆周长或面积执行结果:温度…...
C#学习记录——接口的实现
一小部分知识精英依旧直面核心困难,努力地进行深度钻研,生产内容;而大多数信息受众始终在享受轻度学习,消费内容。如果我们真的希望在时代潮流中占据一席之地,那就应该尽早抛弃轻松学习的幻想,锤炼深度学习…...

“ChatGPT之父”Sam Altman:我是如何成功的?
背靠微软,OpenAI能拳打谷歌,脚踢Meta,它背后的男人,必然不简单。 让我们来看一看,Sam Altman是如何一步步成长为今天这个搅动全世界的男人。 山姆奥特曼(Sam Altman) 成长和创业经历 在YC创始…...

jQuery发送Ajax请求的几种方式
概述JQuery发送ajax请求的方法有很多,其中最基本的方法是$.ajax,在其中封装的方法有 $.get, $post等。我们分别举了不同的示例。数据格式首先,浏览器与服务器之间传输数据所采用的格式,比较常见的有json,jsonp…...
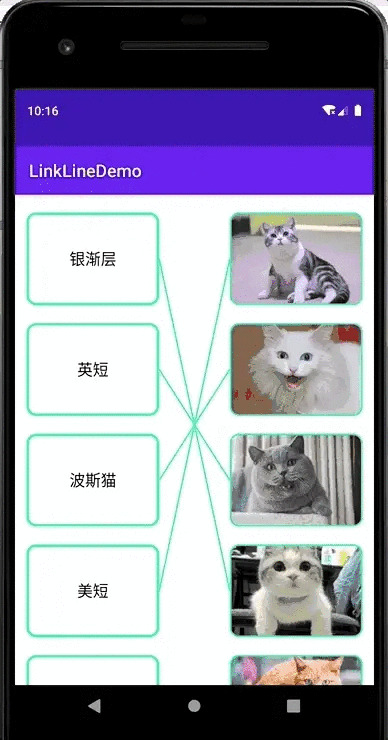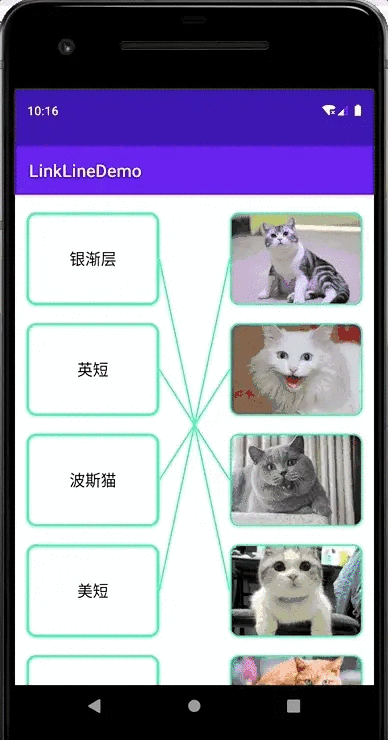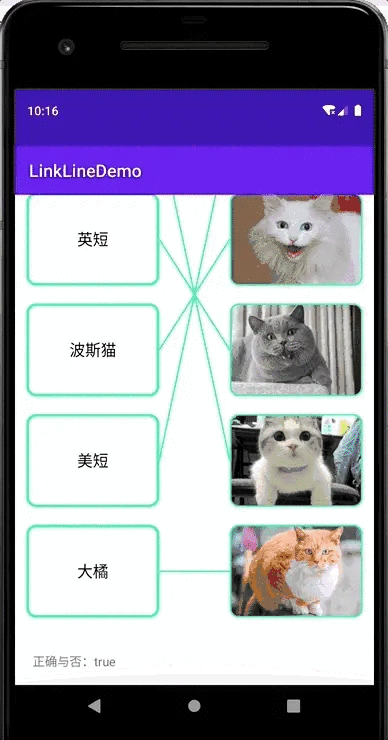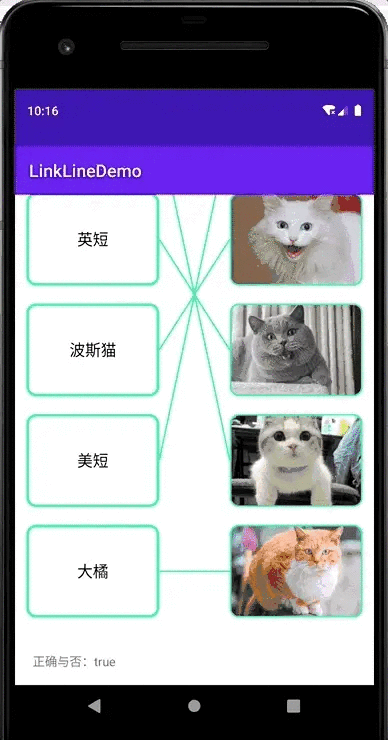
Android实现连线题效果
效果图全部正确:有对有错:结果展示,纯黑色:支持图片:实现思路仔细分析可以发现,连线题的布局可以分为两部分,一个是左右两列矩形,另一个是他们之间的连线。每个矩形的宽高都一样&…...

以数据 见未来!首届未来数商大会成功举办
2月25日,2023未来数商大会在杭州未来科技城学术交流中心举办。大会发布了数商产业趋势研究报告,首次提出并探讨了完整的数商产业概念,并成立了未来数商联盟,开通了浙江大数据交易服务平台余杭专区。会上,杭州未来科技城…...
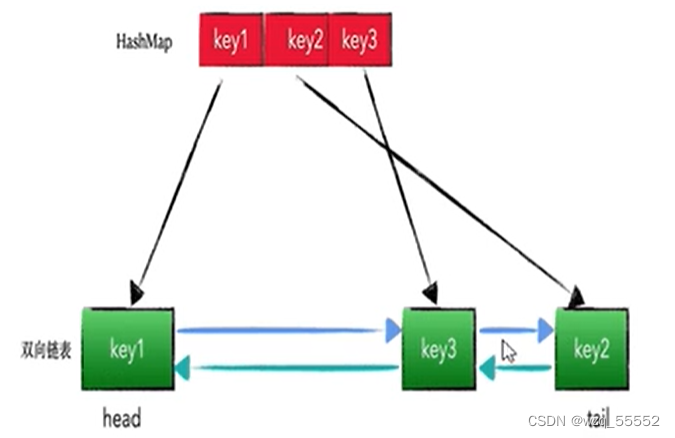
Java数据结构与算法——手撕LRULFU算法
LRU算法 力扣146:https://leetcode-cn.com/problems/lru-cache/ 讲解视频:https://www.bilibili.com/video/BV1Hy4y1B78T?p65&vd_source6f347f8ae76e7f507cf6d661537966e8 LRU是Least Recently Used的缩写,是一种常用的页面置换算法&…...

20230227英语学习
Can Clay Capture Carbon Dioxide? 低碳新思路:粘土也能吸收二氧化碳! The atmospheric level of carbon dioxide — a gas that is great at trapping heat, contributing to climate change — is almost double what it was prior to the Industria…...

校招前端高频react面试题合集
了解redux吗? redux 是一个应用数据流框架,主要解决了组件之间状态共享问题,原理是集中式管理,主要有三个核心方法:action store reduce 工作流程 view 调用store的dispatch 接受action传入的store,reduce…...
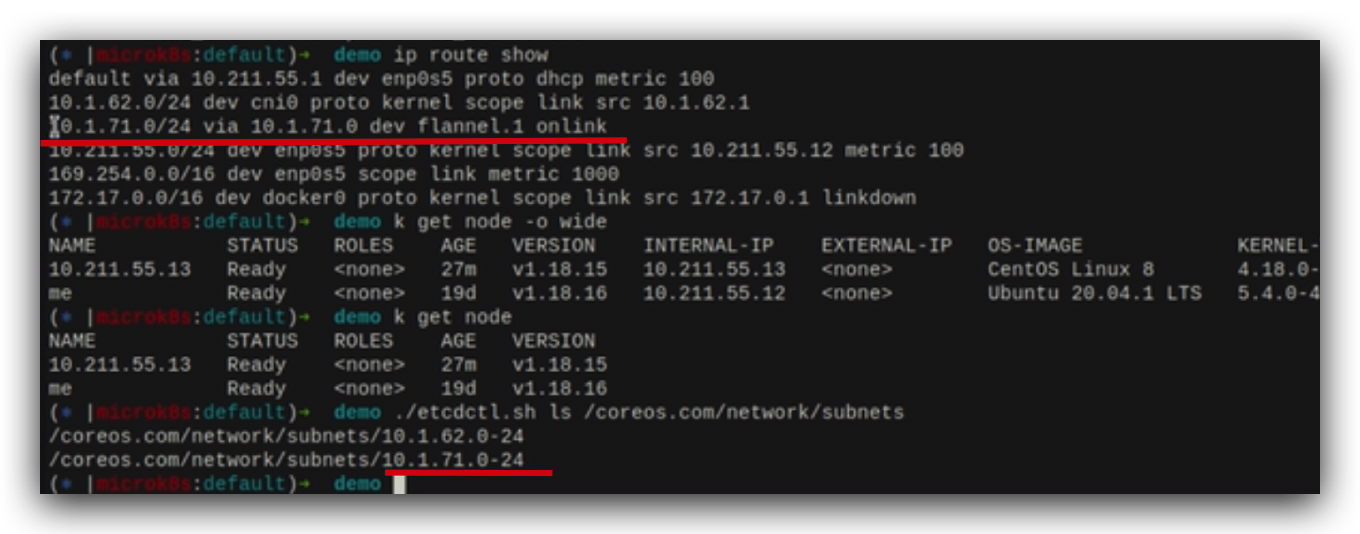
k8s node之间是如何通信的?
承接上文同一个node中pod之间如何通信?单一Pod上的容器是怎么共享网络命名空间的?每个node上的pod ip和cni0网桥ip和flannel ip都是在同一个网段10.1.71.x上。cni0网桥会把报文发送flannel这个网络设备上,flannel其实是node上的一个后台进程&…...
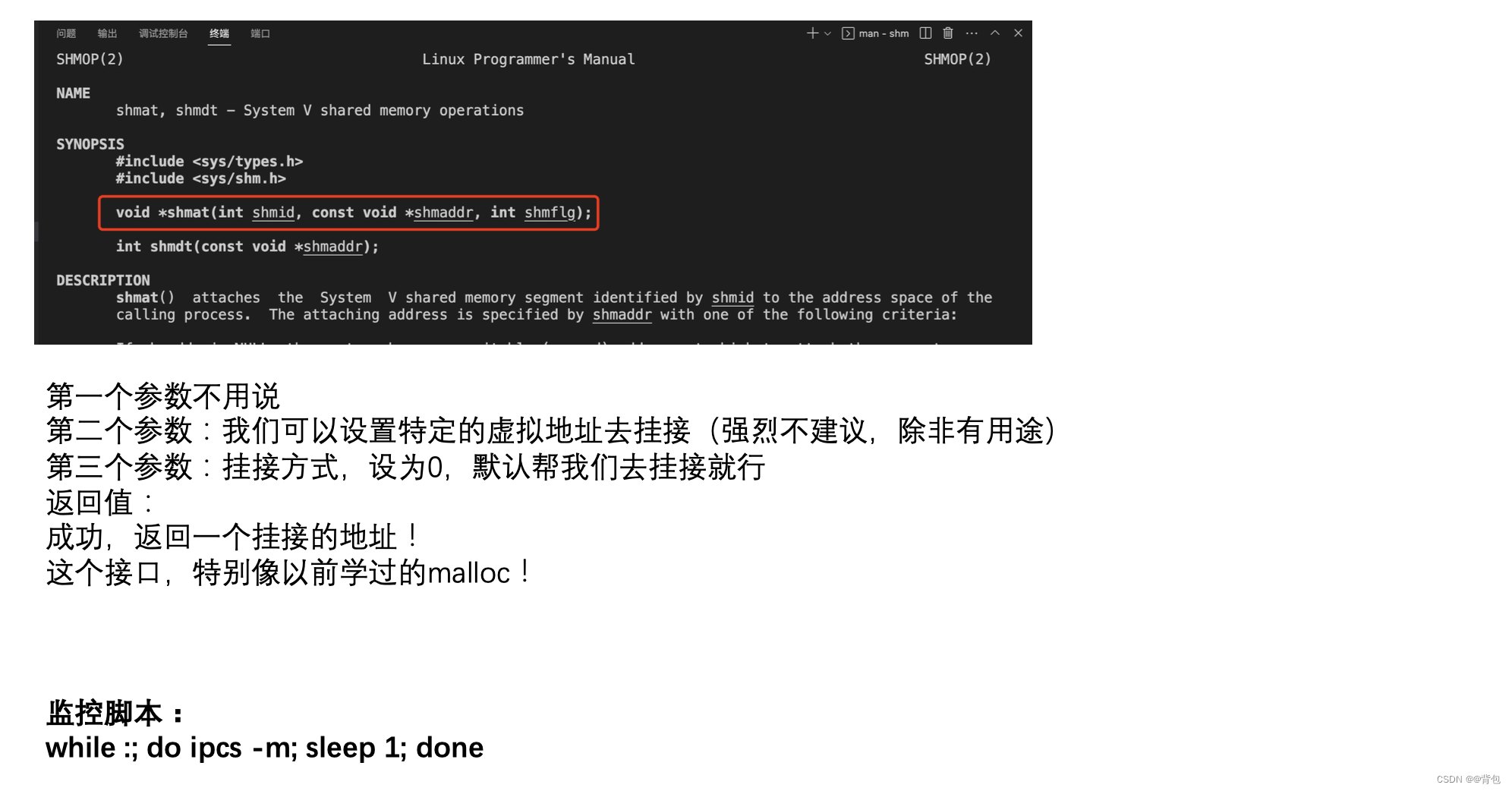
System V|共享内存基本通信框架搭建|【超详细的代码解释和注释】
前言 那么这里博主先安利一下一些干货满满的专栏啦! 手撕数据结构https://blog.csdn.net/yu_cblog/category_11490888.html?spm1001.2014.3001.5482这里包含了博主很多的数据结构学习上的总结,每一篇都是超级用心编写的,有兴趣的伙伴们都支…...
魔兽世界WoW注册网站搭建——-Liunx
问题背景哎 搭建了一个魔兽3.35(纯洁版)每当同学朋友要玩的时候我都直接worldserver上面打一个命令随之出现朋友的朋友也要玩想了想还是要有一个网站原本以为吧单机版里面网页的IP数据库改下可以了结果PHP报错了Unknown column sha_pass_hash in field l…...

OSG三维渲染引擎编程学习之六十八:“第六章:OSG场景工作机制” 之 “6.8 OSG内存管理”
目录 第六章 OSG场景工作机制 6.8 OSG内存管理 6.8.1 Referenced类 6.8.2 ref_ptr<>模板类 6.8.3 智能指针...

字节前端必会面试题(持续更新中)
事件传播机制(事件流) 冒泡和捕获 谈一谈HTTP数据传输 大概遇到的情况就分为定长数据 与 不定长数据的处理吧。 定长数据 对于定长的数据包而言,发送端在发送数据的过程中,需要设置Content-Length,来指明发送数据的长度。 当…...

内存数据库-4-[redis]在ubuntu中离线安装
Ubuntu20.04(linux)离线安装redis 官网redis下载地址 下载安装包redis-6.0.9.tar.gz。 1 下载安装 (1)解压 sudo tar -xzvf redis-6.0.9.tar.gz -C /usr/local/ cd /usr/local/redis-6.0.9/(2)编译 sudo make(3)测试 sudo dpkg -i libtcl8.6_8.6.10dfsg-1_amd64.deb sudo d…...
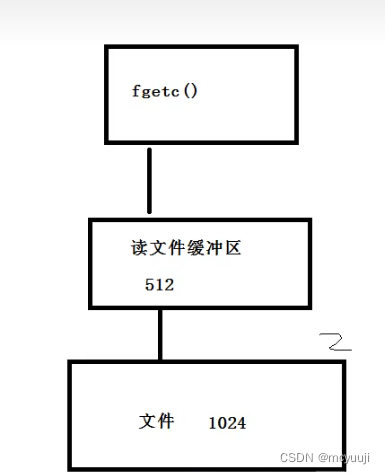
并非从0开始的c++ day8
并非从0开始的c day8结构体结构体嵌套二级指针练习结构体偏移量内存对齐内存对齐的原因如何内存对齐文件操作文件的概念流的概念文本流二进制流文件缓冲区文件打开关闭文件关闭fclose文件读写函数回顾按格式化读写文件文件读写注意事项结构体 结构体嵌套二级指针练习 需求&am…...
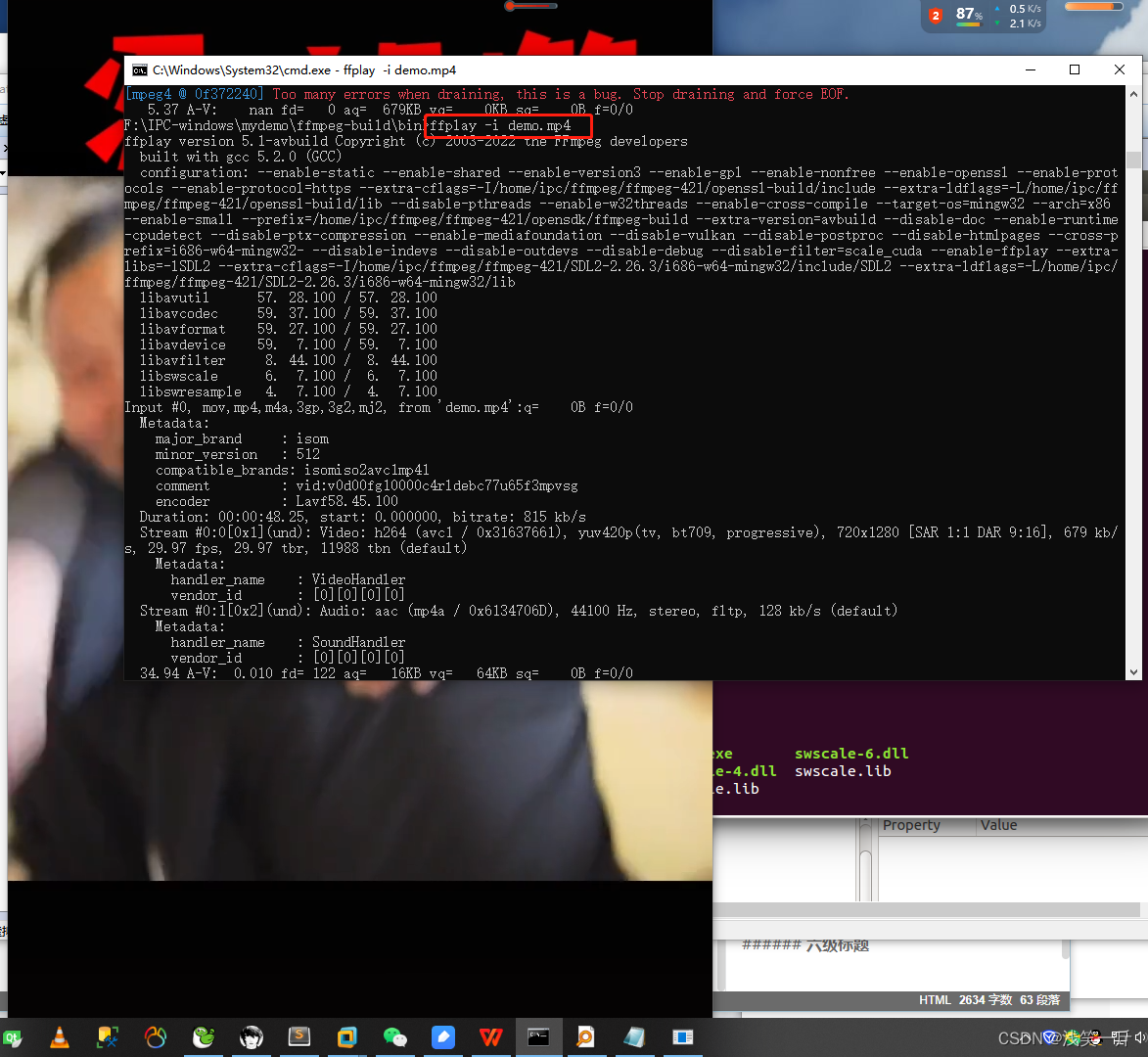
ubuntu下用i686-w64-mingw32交叉编译支持SDL、Openssl的ffmpeg库
前言 本篇博客是基于前两篇关于ffmpeg交叉编译下,进行再次编译操作。ubuntu下ffmpeg的交叉编译环境搭建可以参看以下我的这篇博客:https://blog.csdn.net/linyibin_123/article/details/108759367 ; ubuntu下交叉编译openssl及交叉编译支持o…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
