【聚类】谱聚类解读、代码示例
【聚类】谱聚类详解、代码示例
文章目录
- 【聚类】谱聚类详解、代码示例
- 1. 介绍
- 2. 方法解读
- 2.1 先验知识
- 2.1.1 无向权重图
- 2.1.2 拉普拉斯矩阵
- 2.2 构建图(第一步)
- 2.2.1 ϵ\epsilonϵ 邻近法
- 2.2.2 k 近邻法
- 2.2.3 全连接法
- 2.3 切图(第二步)
- 2.3.1 最小化 cut (A1, A2, . . . Ak)\text{cut (A1, A2, . . . Ak)}cut (A1, A2, . . . Ak)
- 2.3.2 RatioCut 切图
- 2.3.3 Ncut切图
- 3. 谱聚类流程
- 3.1 输入与输出
- 3.2 一般流程
- 4. 代码演示
- 5. 总结
- 6. 参考
1. 介绍
谱聚类的基本原理:
- 把所有数据看成空间中的点,这些点之间可以用变连接起;
- 距离较远的两个点之间的边权重较低,而距离较近的两个点之间的边权重较高;
- 通过对所有数据点组成的图进行切图,让切图后的不同的子图间边权重和尽可能小(即距离远),而子图内的边权重和尽可能高(即距离近)。
难点:
- 如何构建图?
- 如何切分图?
2. 方法解读
2.1 先验知识
2.1.1 无向权重图

2.1.2 拉普拉斯矩阵

2.2 构建图(第一步)
2.2.1 ϵ\epsilonϵ 邻近法

2.2.2 k 近邻法

2.2.3 全连接法
比前两种方法,第三种方法所有的点之间的权重值都大于0,因此称之为全连接法。
- 可以选择不同的核函数来定义边权重,常用的有多项式核函数,高斯核函数和Sigmoid核函数。
- 最常用的是高斯核函数 RBF。

2.3 切图(第二步)

其中Aiˉ\bar {\text{A}_i}Aiˉ 为 A\text{A}A 的补集。
进而,如何切图使子图内的点权重高,子图之间的点权重低?
2.3.1 最小化 cut (A1, A2, . . . Ak)\text{cut (A1, A2, . . . Ak)}cut (A1, A2, . . . Ak)
一个自然的想法就是最小化 cut (A1, A2, . . . Ak)\text{cut (A1, A2, . . . Ak)}cut (A1, A2, . . . Ak),但是可以发现,这种极小化的切图存在问题,如下图:
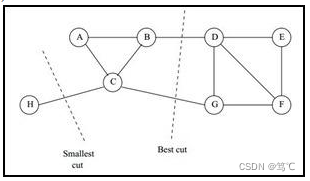
- 为了避免最小切图导致的切图效果不佳,我们需要对每个子图的规模做出限定;
- 一般来说,有两种切图方式,第一种是 RatioCut,第二种是 Ncut。
2.3.2 RatioCut 切图
对于每个切图,不仅要考虑最小化 cut (A1, A2, . . . Ak)\text{cut (A1, A2, . . . Ak)}cut (A1, A2, . . . Ak),还要考虑最大化每个子图样本的个数,即最小化 RatioCut函数:
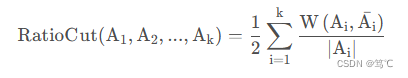

- 这里需要提一下,hih_ihi是正交基,但并不是单位正交基,因为hiThi=1∣Aj∣{h_i}^Th_i = \frac{1}{|A_j|}hiThi=∣Aj∣1,而不是1。但是不影响后面结论。
2.3.3 Ncut切图


3. 谱聚类流程
3.1 输入与输出
- 输入:样本集 D=(x1,x2,...,xn)D=(x_1, x_2,...,x_n)D=(x1,x2,...,xn),邻接矩阵的生成方式,降维后的维度k1,聚类方法,聚类后的簇个数k2;
- 输出: 簇划分C(c1,c2,...,ck2)C ( c_1, c_2,. . .,c_{k2})C(c1,c2,...,ck2)
3.2 一般流程
- 根据邻接矩阵生成方式构建邻接矩阵W,构建度矩阵D;
- 计算出拉普拉斯矩阵L;
- 构建标准化后的拉普拉斯矩阵D−12LD−12D^{-\frac {1}{2}}LD^{-\frac {1}{2}}D−21LD−21;
- 计算D−12LD−12D^{-\frac {1}{2}}LD^{-\frac {1}{2}}D−21LD−21最小的k1个特征值所各自对应的特征向量f;
- 将各自对应的特征向量f组成的矩阵按行标准化,最终组成n × k1 维矩阵F;
- 对F 中的每一行作为一个k1维样本,共n个样本,用输入的聚类方法进行聚类,聚类个数为k2;
- 得到簇划分C(c1,c2,...,ck2)C ( c_1, c_2,. . .,c_{k2})C(c1,c2,...,ck2)。
4. 代码演示
import numpy as np
import matplotlib.pyplot as plt
from sklearn import cluster, datasets
from sklearn.preprocessing import StandardScalernp.random.seed(0)# 数据构造
n_samples = 1500
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=0.2, noise=0.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=0.05)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)data_sets = [(noisy_circles, {"n_clusters": 3}),(noisy_moons, {"n_clusters": 2}), (blobs, {"n_clusters": 3})
]
colors = ["#377eb8", "#ff7f00", "#4daf4a"]
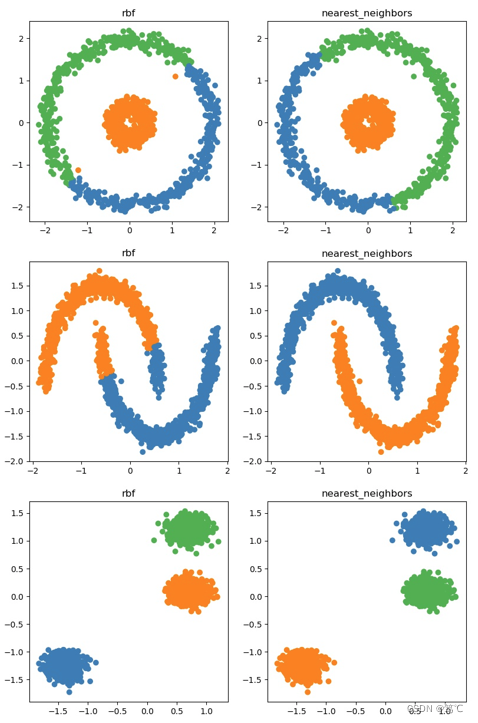
affinity_list = ['rbf', 'nearest_neighbors']plt.figure(figsize=(20, 15))for i_dataset, (dataset, algo_params) in enumerate(data_sets):params = algo_paramsX, y = datasetX = StandardScaler().fit_transform(X)for i_affinity, affinity_strategy in enumerate(affinity_list):spectral = cluster.SpectralClustering(n_clusters=params['n_clusters'],eigen_solver='arpack', affinity=affinity_strategy)spectral.fit(X)y_pred = spectral.labels_.astype(int)y_pred_colors = []for i in y_pred:y_pred_colors.append(colors[i])plt.subplot(3, 4, 4*i_dataset+i_affinity+1)plt.title(affinity_strategy)plt.scatter(X[:, 0], X[:, 1], color=y_pred_colors)# plt.show()
plt.savefig("a.jpg")
5. 总结
- 优点:
- 谱聚类只需要数据之间的邻接矩阵,因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到;
- 由于使用了降维,因此在处理高维数据聚类时的复杂度比传统聚类算法好。
- 缺点:
- 如果最终聚类的维度非常高,则由于降维的幅度不够,谱聚类的运行速度和最后的聚类效果均不好;
- 聚类效果依赖于邻接矩阵,不同的邻接矩阵得到的最终聚类效果可能很不同。
6. 参考
【1】https://blog.csdn.net/qq_42735631/article/details/121010760
相关文章:

【聚类】谱聚类解读、代码示例
【聚类】谱聚类详解、代码示例 文章目录【聚类】谱聚类详解、代码示例1. 介绍2. 方法解读2.1 先验知识2.1.1 无向权重图2.1.2 拉普拉斯矩阵2.2 构建图(第一步)2.2.1 ϵ\epsilonϵ 邻近法2.2.2 k 近邻法2.2.3 全连接法2.3 切图(第二步…...
,简介)
最牛逼的垃圾回收期ZGC(1),简介
1丶什么是ZGC? ZGC是JDK 11中引入的一种可扩展的、低延迟的垃圾收集器。ZGC最主要的特点是:在非常短的时间内(一般不到10ms),就可以完成一次垃圾回收,而且这个时间是与堆的大小无关的。另外,ZGC支持非常大…...

微服务的Feign到底是什么
Feign是什么 分区是一种数据库优化技术,它可以将大表按照一定的规则分成多个小表,从而提高查询和维护的效率。在分区的过程中,数据库会将数据按照分区规则分配到不同的分区中,并且可以在分区中使用索引和其他优化技术来提高查询效…...

JavaScript 正则表达式
正则表达式(英语:Regular Expression,在代码中常简写为regex、regexp或RE)使用单个字符串来描述、匹配一系列符合某个句法规则的字符串搜索模式。搜索模式可用于文本搜索和文本替换。什么是正则表达式?正则表达式是由一…...

【批处理脚本】-1.15-文件内字符串查找命令find
"><--点击返回「批处理BAT从入门到精通」总目录--> 共7页精讲(列举了所有find的用法,图文并茂,通俗易懂) 在从事“嵌入式软件开发”和“Autosar工具开发软件”过程中,经常会在其集成开发环境IDE(CodeWarrior,S32K DS,Davinci,EB Tresos,ETAS…)中,…...
【手撕面试题】JavaScript(高频知识点二)
目录 面试官:请你谈谈JS的this指向问题 面试官:说一说call apply bind的作用和区别? 面试官:请你谈谈对事件委托的理解 面试官:说一说promise是什么与使用方法? 面试官:说一说跨域是什么&a…...

Web学习1_HTML
在学校期间学的Web知识忘了一些,很多东西摸棱两可,现重新系统的学习一下。 首先下载安装完vsc后并下载拓展文件live server(模拟一个服务器) Auto Rename Tag(在写网页时,自动对齐前后标签)在设…...
)
华为OD机试真题Java实现【靠谱的车】真题+解题思路+代码(20222023)
靠谱的车 题目 程序员小明打了一辆出租车去上班。出于职业敏感,他注意到这辆出租车的计费表有点问题,总是偏大。 出租车司机解释说他不喜欢数字4,所以改装了计费表,任何数字位置遇到数字4就直接跳过,其余功能都正常。 比如: 23再多一块钱就变为25; 39再多一块钱变…...
【C++入门(下篇)】C++引用,内联函数,auto关键字的学习
前言: 在上一期我们进行了C的初步认识,了解了一下基本的概念还学习了包括:命名空间,输入输出以及缺省参数等相关的知识。今天我们将进一步对C入门知识进行学习,主要还需要大家掌握我们接下来要学习的——引用…...

基于合作型Stackerlberg博弈的考虑差别定价和风险管理的微网运行策略研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

2023年全国最新保安员精选真题及答案8
百分百题库提供保安员考试试题、保安职业资格考试预测题、保安员考试真题、保安职业资格证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 81.以下各组情形都属于区域巡逻中异常情况的是()。 A&#x…...

JavaScript高级程序设计读书分享之6章——MapSet
JavaScript高级程序设计(第4版)读书分享笔记记录 适用于刚入门前端的同志 Map 作为 ECMAScript 6 的新增特性,Map 是一种新的集合类型,为这门语言带来了真正的键/值存储机制。Map 的大多数特性都可以通过 Object 类型实现,但二者之间还是存在…...
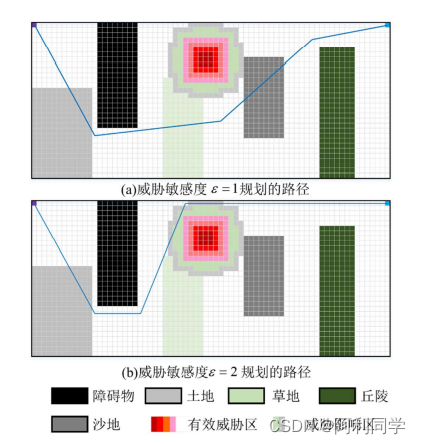
改进的 A*算法的路径规划(路径规划+代码+毕业设计)
引言 近年来,随着智能时代的到来,路径规划技术飞快发展,已经形成了一套较为成熟的理论体系。其经典规划算法包括 Dijkstra 算法、A算法、D算法、Field D算法等,然而传统的路径规划算法在复杂的场景的表现并不如人意,例…...

Tina_Linux存储性能参考指南
OpenRemoved_Tina_Linux_存储性能_参考指南 1 概述 1.1 编写目的 介绍TinaLinux 存储性能的测试方法和历史数据,提供参考。 1.2 适用范围 Tina V3.0 及其后续版本。 1.3 相关人员 适用于TinaLinux 平台的客户及相关技术人员。 2 经验性能值 Flash 性能与实…...

NCRE计算机等级考试Python真题(四)
第四套试题1、以下选项中,不属于需求分析阶段的任务是:A.需求规格说明书评审B.确定软件系统的性能需求C.确定软件系统的功能需求D.制定软件集成测试计划正确答案: D2、关于数据流图(DFD)的描述,以下选项中正…...

LeetCode每周刷题总结2.20-2.26
本栏目记录本人每周写的力扣题的相关学习总结。 虽然开新的栏目都没有完成 70.爬楼梯 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 解题思路: 斐波那契数列递归 class Solution {…...

u盘里删除的文件可以恢复吗?分享解决方法
u盘里删除的文件可以恢复吗?不知道使用过U盘的你,是否遇到过这样的问题呢?其实正常情况下,在电脑中操作u盘,并删除相关的文件,删除的文件是不会经过电脑回收站的。想要找回就需要借助相关的恢复工具才能实现。下面小编给大家分享…...
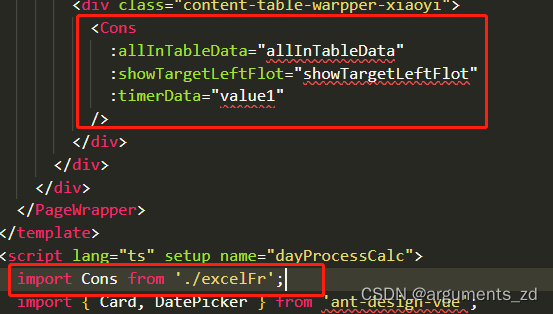
十、vben框架如何使用table来写报表
在项目开发的过程中,有很多特殊的table样式,有的时候后端会用帆软来写报表,但是有的特殊的报表后端就不能支持实现了,那么前端是如何实现的呢,今天我们就来讲讲。 先上效果图: 本次使用的tsx组件来写的报表…...

jQuery:入门
jQuery 入门 Date: January 19, 2023 目标: 能够说出什么是 jQuery 能够说出 jQuery 的优点 能够简单使用 jQuery 能够说出 DOM 对象和 jQuery 对象的区别 jQuery 概述 JavaScript 库 仓库: 可以把很多东西放到这个仓库里面。找东西只需要到仓库里…...

实例3:树莓派呼吸灯
实例3:树莓派呼吸灯 实验目的 通过背景知识学习,了解digital与analog的区别。通过GPIO对外部LED灯进行呼吸控制,熟悉PWM技术。 实验要求 通过python编程,用GPIO控制LED灯,使之亮度逐渐增大,随后减小&am…...

Lab4AI上线一键部署OpenClaw,附2分钟云养虾指南
Lab4AI上线一键部署OpenClaw,附2分钟云养虾指南 “养虾”这件事,最近很火。 在 AI 自动化工具高速发展的今天,OpenClaw 作为一款开源 AI 代理与自动化平台,正以其出色的灵活性和兼容性,成为许多人打造专属智能助手的优…...
对dreamlike风格影响)
Jimeng LoRA参数详解:LoRA权重精度(fp16/bf16)对dreamlike风格影响
Jimeng LoRA参数详解:LoRA权重精度(fp16/bf16)对dreamlike风格影响 1. 项目背景与测试环境 Jimeng(即梦)LoRA是一个专注于生成梦幻风格图像的轻量级模型,基于Z-Image-Turbo文生图底座构建。这个测试系统专…...

Oh My Zsh 使用指南:Zsh 终端配置与插件管理教程
carbon在 Linux 或 macOS 系统中,终端是开发者和运维人员每天都会使用的重要工具。 默认的 Bash 终端虽然功能完整,但在使用体验和效率方面还有很大的提升空间。 例如: 命令自动补全 终端主题美化 插件扩展 Git 快捷命令 因此很多开发者会…...

终极JUCE音频元数据编辑工具实战指南:高效管理音乐资产
终极JUCE音频元数据编辑工具实战指南:高效管理音乐资产 【免费下载链接】JUCE 项目地址: https://gitcode.com/gh_mirrors/juce/JUCE JUCE是一个功能强大的跨平台C应用框架,特别在音频处理领域表现卓越。本文将详细介绍如何利用JUCE框架中的音频…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...
