改进的 A*算法的路径规划(路径规划+代码+毕业设计)
引言
近年来,随着智能时代的到来,路径规划技术飞快发展,已经形成了一套较为成熟的理论体系。其经典规划算法包括 Dijkstra 算法、A算法、D算法、Field D算法等,然而传统的路径规划算法在复杂的场景的表现并不如人意,例如复杂的越野环境。针对越野环境规划问题以及规划算法的优劣性,选择改进 A算法来进行越野环境路径规划
通过越野栅格环境建模、通行方向变化惩罚、局部区域复杂度惩罚和路径平滑的方法对传统 A*算法进行改进,以满足复杂越野环境下,不同类型的智能车辆和不同任务的安全行驶、高效通行综合要求。
重要代码
###############构造地图################
#宽高W,H。
class Array2D:#初始化def __init__(self,w,h):self.w=wself.h=hself.data=[]self.data=[[0.0 for y in range(h)] for x in range(w)]#显示地图def showArray2D(self):for y in range(self.h):for x in range(self.w):print(self.data[x][y],end=' ')print("")#获得任意节点信息 ,__getitem__()魔法函数作用为当实例化对象map进行map[key]操作上自动调用。def __getitem__(self, item):return self.data[item]###############创建点类################
class Point:#初始化def __init__(self,x,y):self.x=xself.y=y#判断是否同一个点def __eq__(self, other):if self.x==other.x and self.y==other.y:return Truereturn False#打印点信息def __str__(self):return "x:"+str(self.x)+",y:"+str(self.y)##全部代码请联系---->qq1309399183<---------传统 A*算法
在启发式搜索算法中, A算法是其中最为典型的代表,它在全局路径规划算法中,具有快速、高效和准确的优点,因此在智能车辆和工业机器人的路径规划问题上得到了广泛的应用。针对规划路径的需求和任务的要求,许多学者对传统 A算法进行改进,例如:路径的长度、规划效率和拐点数等方面。(下图为传统A*算法流程)
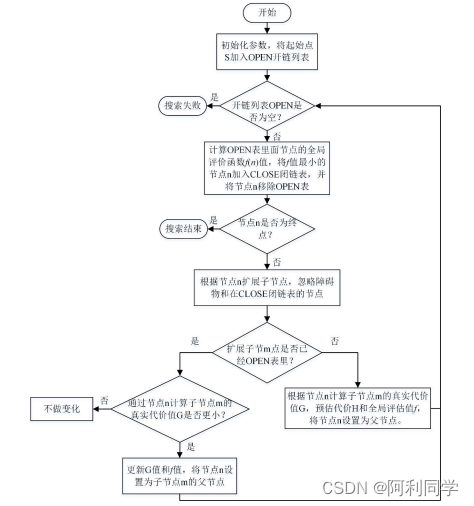
传统 A*算法缺点分析
虽然传统的 A算法在一些简单的场景具有一定的有效性,但是实际的用途中,环境复杂性对于算法实时的要求,传统的 A算法并无法满足要求。只有对传统算法的局限性进行深入了解分析才能更好的在传统方法之上进行更进一步的改进,因此本小节深入分析传统 A算法的局限性和不足,具体有:
(1)栅格地图建模的不足:
首先要意识到的是处理的是离散数据,而不是现实世界中的“连续”地形。采样的数字地形图像是真实地形的近似值,应该在一个理想的高分辨率采样。数字地形图像的分辨率越高,对真实地形的描述越逼真,寻径精度也越高。然而,在分辨率上存在一个上限,超过这个上限后,道路就不再更加精确,并且会不必要地增加寻径算法的运行时间。而且传统的建模方式只限定为可行驶区域和障碍物区域,然而
现实世界环境是及其复杂的,例如可行驶区域可区分为不同道路,沙地、草地、土质路面等等;障碍物也区分有树、行人、车辆建筑物等等。
(2)邻域节点选择不足:
为了找到从起始节点到目标节点的路径,我们必须定义一种选择后续节点的方式。我们可以从一个给定的位置移动到哪里?在现实世界中,一个人可以朝着喜欢的任何方向前进,但在数字地形图上,我们的选择更受限制。传统的 A算法中有两种常见的方法:4 个邻接和 8 个邻接。4 个邻接限制移动在北、南、西、东四64 个主要风向。8 邻接的移动更自由,因为它除了 4 邻接的方向外,还可以在东北、西北、西南和东南方向移动。
(3)算法无法自适应满足不同任务要求:
在不同的任务要求中,有的任务要保证路径的最短,则设计预估代价小于真实代价,但是效率低下;有的任务要保证效率的高效,设计预估代价大于真实代价,但是规划的路径不是最优。
(4)对于大地图算法计算效率不足:
对于现实的环境场景,可能寻找道路的搜索空间非常大,这意味着必须采取措施确保内存不会耗尽,或者搜索不会花费过多的时间运行。即使是一个相对较小的300 × 300 像素的地形图也有 9 万个节点的搜索空间。
越野环境下的 A*算法
障碍物模型:
传统的 A*算法的构建方式中最普遍应用的是栅格法,其基本的思路是把智能车辆的工作空间分割为尺寸一致的网格,并通过数据矩阵来记录环境数据。常规的栅格算法把物理环境严格区分为自由区域和障碍物区域,从而使得数值矩阵能够简化为 0-1 矩阵,0 为自由空间,1 为障碍物空间。如假设智能车的工作空间为
R C ,M 为数值矩阵,表示所有的环境信息,则常规的环境模型可以表示为。

很明显,常规的栅格模型是无法模拟出真实复杂的越野环境,因此本文研究越
野环境的真实场景,建立多层次栅格模型,将越野环境模型细分为障碍物模型,威
胁模型和道路模型,如图 所示。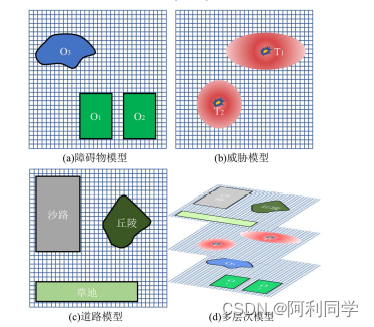
威胁模型

子节点优化选择策略
(1)子节点选择方式
为了找到从起始点到终点的路径,需定义一种可以选择后续节点的方式。在A*算法中两种常见的方法为 4-邻接(见图 5-7(a))和 8-邻接 (见图 5-7(b)),但考虑到在复杂越野环境上,我们希望智能车辆允许更多的自由运动来更好规避危险,因此本文选择 16-邻接(见图 5-7©)。如图 5-8 所示,4-邻接规划的路径具有很多的直角拐点且路径最长,其次是 8-邻接规划的路径,而 16-邻接规划的路径平滑、拐点数少、路径短,适合复杂越野环境智能车的需求。
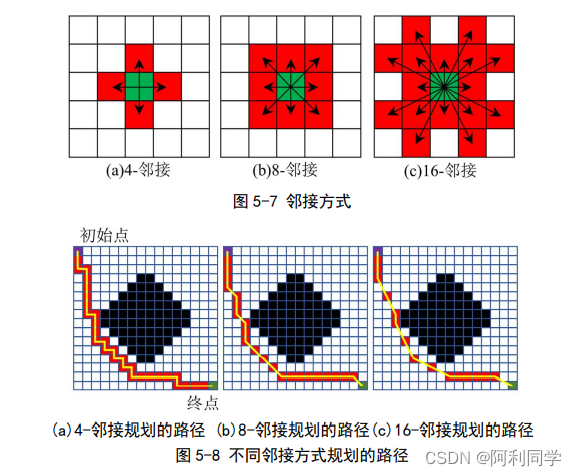
(2)优化子节点选择
传统 A*算法在子节点选取上,仅考察子节点周围是否为障碍物,而未考察子节点与障碍物位置的相关性,从而规划出路线存在斜着通过障碍物栅格顶点的问题,导致车辆可能与障碍物发生碰撞。因为本文中所构建环境模型具有更危险的威胁物存在,所以优化了子节点的选择规则。
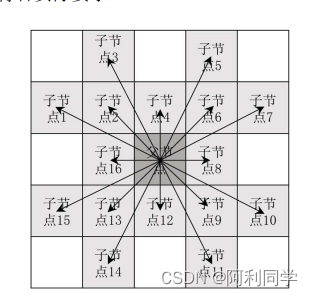
如图 5-9,为 16 个子节点分布图。本文结合越野环境栅格地图设计的子节点选择规则为:
**1:**若子节点 4 或子节点 12 具有威胁(在越野环境栅格地图中值1),则子节点 2、子节点 6、子节点 3、子节点 5 或子节点 13、子节点 9、子节点 14、子节点11 不作为预选点。
**2:**若子节点 16 或子节点 8 具有威胁,则子节点 2、子节点 13、子节点 15、
子节点 1 或子节点 6、子节点 9、子节点 10、子节点 7 不作为预选点。
**3:**均无具威胁,则不做处理。
优化子节点选择后,规划后的路径避开具有威胁栅格的顶点,避免智能车辆
代码部分
###############创建A-Star类############
class AStar:# 描述AStar算法中的节点数据class Node: #初始化def __init__(self, point, startPoint,endPoint, g=0,w=1,p=1):self.point = point # 自己的坐标self.father = None # 父节点self.g = g # g值,g值在用到的时候会重新算# 计算h值,采用曼哈顿距离#self.h = (abs(endPoint.x - point.x) + abs(endPoint.y - point.y)) * 10 #采用欧几里得距离#self.h = math.pow((math.pow((endPoint.x - point.x),2) + math.pow((endPoint.y - point.y),2)),0.5)*10#采用对角距离pp=(1-p)+0.2*math.exp((math.pow((math.pow((endPoint.x - point.x),2) + math.pow((endPoint.y - point.y),2)),0.5))/(math.pow((math.pow((endPoint.x - startPoint.x),2) + math.pow((endPoint.y - startPoint.y),2)),0.5)))Diagonal_step = min((endPoint.x - point.x),(endPoint.y - point.y))straight_step = (abs(endPoint.x - point.x) + abs(endPoint.y - point.y)) - 2*Diagonal_stepself.h =(straight_step + math.pow(2,0.5)*Diagonal_step)*10*pp#print(pp)#初始化A-startdef __init__(self, map2d, startPoint, endPoint, passTag=1.0):#map2d地图信息,startPoint起点, endPoint终点, passTag=1.0为不可行驶区域# 开启表self.openList = []# 关闭表self.closeList = []# 寻路地图self.map2d = map2d# 起点终点if isinstance(startPoint, Point) and isinstance(endPoint, Point):self.startPoint = startPointself.endPoint = endPointelse:self.startPoint = Point(*startPoint)self.endPoint = Point(*endPoint)# 不可行走标记self.passTag = passTagdef getMinNode(self):"""获得openlist中F值最小的节点:return: Node"""currentNode = self.openList[0]for node in self.openList:if node.g + node.h < currentNode.g + currentNode.h:currentNode = nodereturn currentNode#返回最小代价的点结果对比
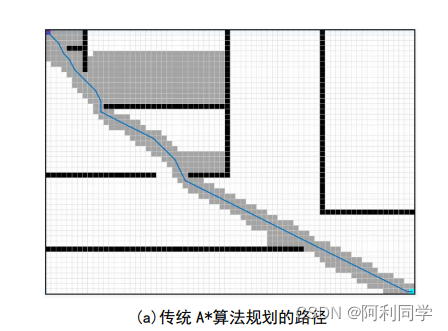
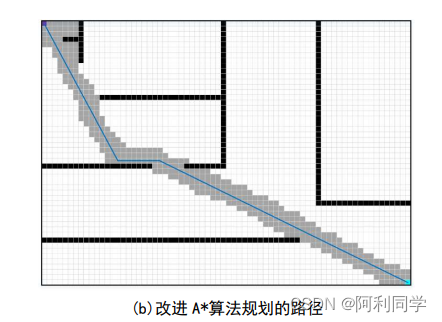
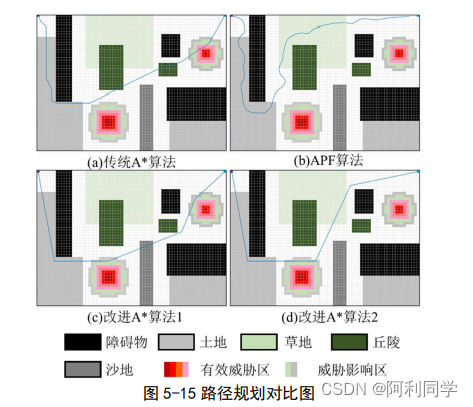
越野环境路径规划对比
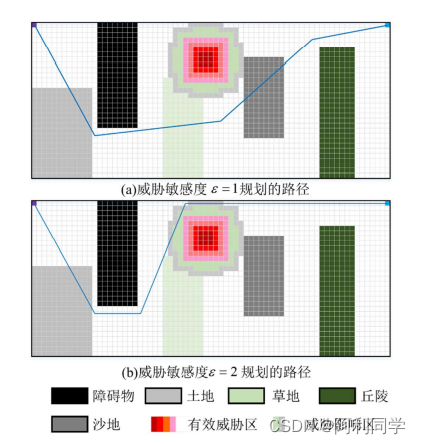
敏感度衡量对比
结论
本节针对越野场景路径规划问题,采用栅格法建立障碍物、威胁物和越野道路模型,模拟真实的越野环境场景。引入方向变化惩罚和局部区域复杂度惩罚来优化A算法,使算法规划出的路径更平滑,算法效率更高效。采用改进 Floyd 算法对路径进行双向平滑,并且进行了防碰撞处理,来确保规划出路径的安全可靠性。仿真结果表明,所改进的 A算法与传统算法相比较,效率提高了 30%,拐点数减少了
4 倍,所提算法能够在越野环境多重因素综合影响以及不同车辆性能和任务的要求下快速的规划出安全的路径。
全部代码可私信
相关文章:

改进的 A*算法的路径规划(路径规划+代码+毕业设计)
引言 近年来,随着智能时代的到来,路径规划技术飞快发展,已经形成了一套较为成熟的理论体系。其经典规划算法包括 Dijkstra 算法、A算法、D算法、Field D算法等,然而传统的路径规划算法在复杂的场景的表现并不如人意,例…...

Tina_Linux存储性能参考指南
OpenRemoved_Tina_Linux_存储性能_参考指南 1 概述 1.1 编写目的 介绍TinaLinux 存储性能的测试方法和历史数据,提供参考。 1.2 适用范围 Tina V3.0 及其后续版本。 1.3 相关人员 适用于TinaLinux 平台的客户及相关技术人员。 2 经验性能值 Flash 性能与实…...

NCRE计算机等级考试Python真题(四)
第四套试题1、以下选项中,不属于需求分析阶段的任务是:A.需求规格说明书评审B.确定软件系统的性能需求C.确定软件系统的功能需求D.制定软件集成测试计划正确答案: D2、关于数据流图(DFD)的描述,以下选项中正…...

LeetCode每周刷题总结2.20-2.26
本栏目记录本人每周写的力扣题的相关学习总结。 虽然开新的栏目都没有完成 70.爬楼梯 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 解题思路: 斐波那契数列递归 class Solution {…...

u盘里删除的文件可以恢复吗?分享解决方法
u盘里删除的文件可以恢复吗?不知道使用过U盘的你,是否遇到过这样的问题呢?其实正常情况下,在电脑中操作u盘,并删除相关的文件,删除的文件是不会经过电脑回收站的。想要找回就需要借助相关的恢复工具才能实现。下面小编给大家分享…...
十、vben框架如何使用table来写报表
在项目开发的过程中,有很多特殊的table样式,有的时候后端会用帆软来写报表,但是有的特殊的报表后端就不能支持实现了,那么前端是如何实现的呢,今天我们就来讲讲。 先上效果图: 本次使用的tsx组件来写的报表…...

jQuery:入门
jQuery 入门 Date: January 19, 2023 目标: 能够说出什么是 jQuery 能够说出 jQuery 的优点 能够简单使用 jQuery 能够说出 DOM 对象和 jQuery 对象的区别 jQuery 概述 JavaScript 库 仓库: 可以把很多东西放到这个仓库里面。找东西只需要到仓库里…...

实例3:树莓派呼吸灯
实例3:树莓派呼吸灯 实验目的 通过背景知识学习,了解digital与analog的区别。通过GPIO对外部LED灯进行呼吸控制,熟悉PWM技术。 实验要求 通过python编程,用GPIO控制LED灯,使之亮度逐渐增大,随后减小&am…...

android适配ipv6,请求慢?
先贴一篇我们经常能搜索到的解决方案: Android 在 4G 下访问 IPV6 慢的解决方案 文章很有参考意义,但也并不是所有请求慢的的原因! 本文是另一种原因,有兴趣就继续往下看一看. 使用的okhttp框架,模式支持ipv6和ipv4协议,但两种协议同时存在时…...
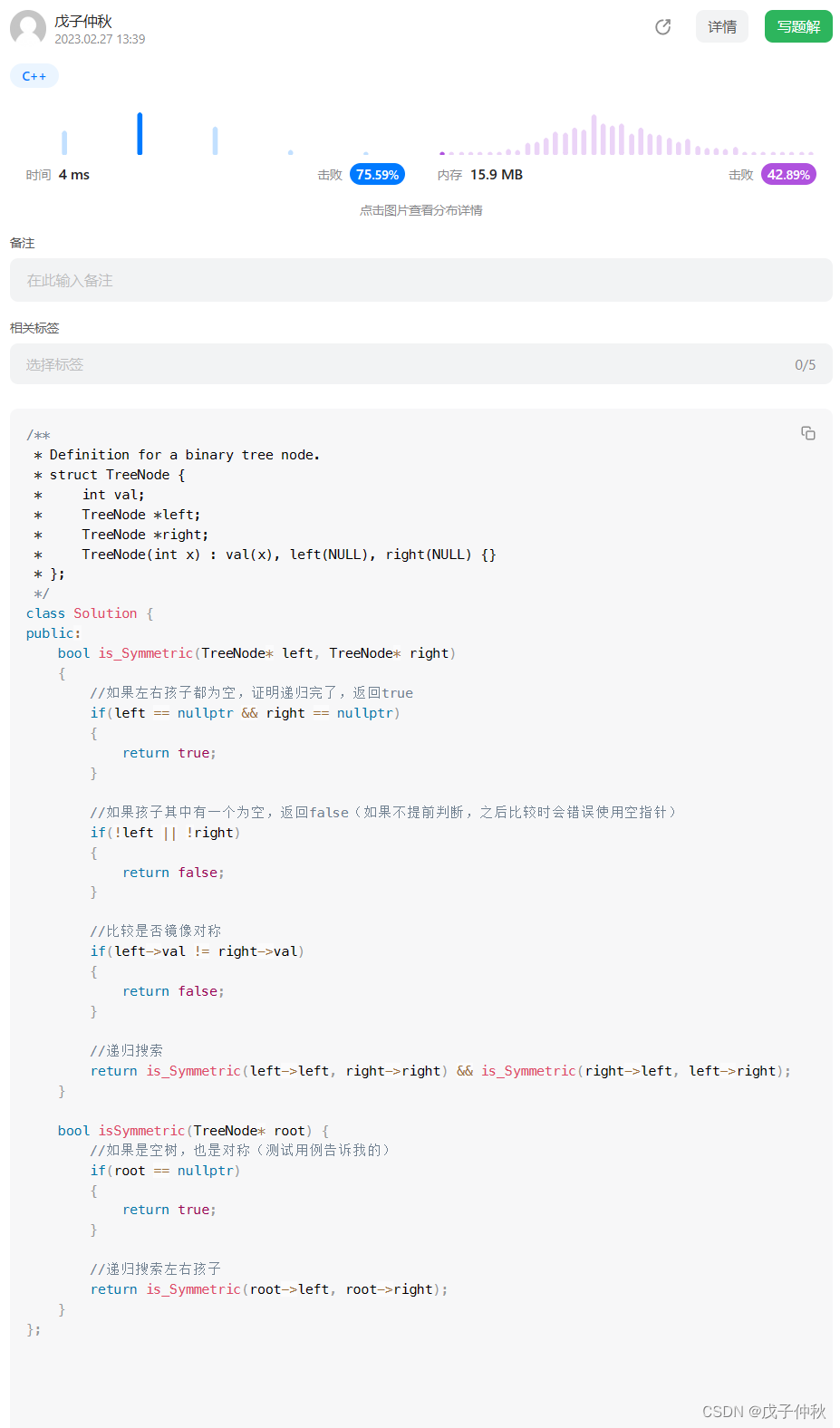
【LeetCode】剑指 Offer(10)
目录 题目:剑指 Offer 27. 二叉树的镜像 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 28. 对称的二叉树 - 力扣࿰…...
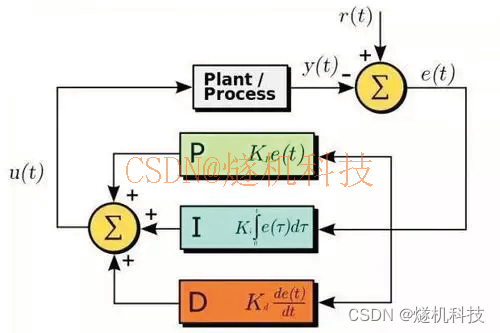
学校AI视频行为分析监测系统 opencv
学校AI视频行为分析监测系统通过pythonopencv网络模型AI视频分析技术,学校AI视频行为分析监测算法对学校区域人员打架行为识别、跌倒行为识别、翻墙识别、人员聚众识别、攀高识别、抽烟行为等进行智能识别预警。OpenCV的全称是Open Source Computer Vision Library&…...
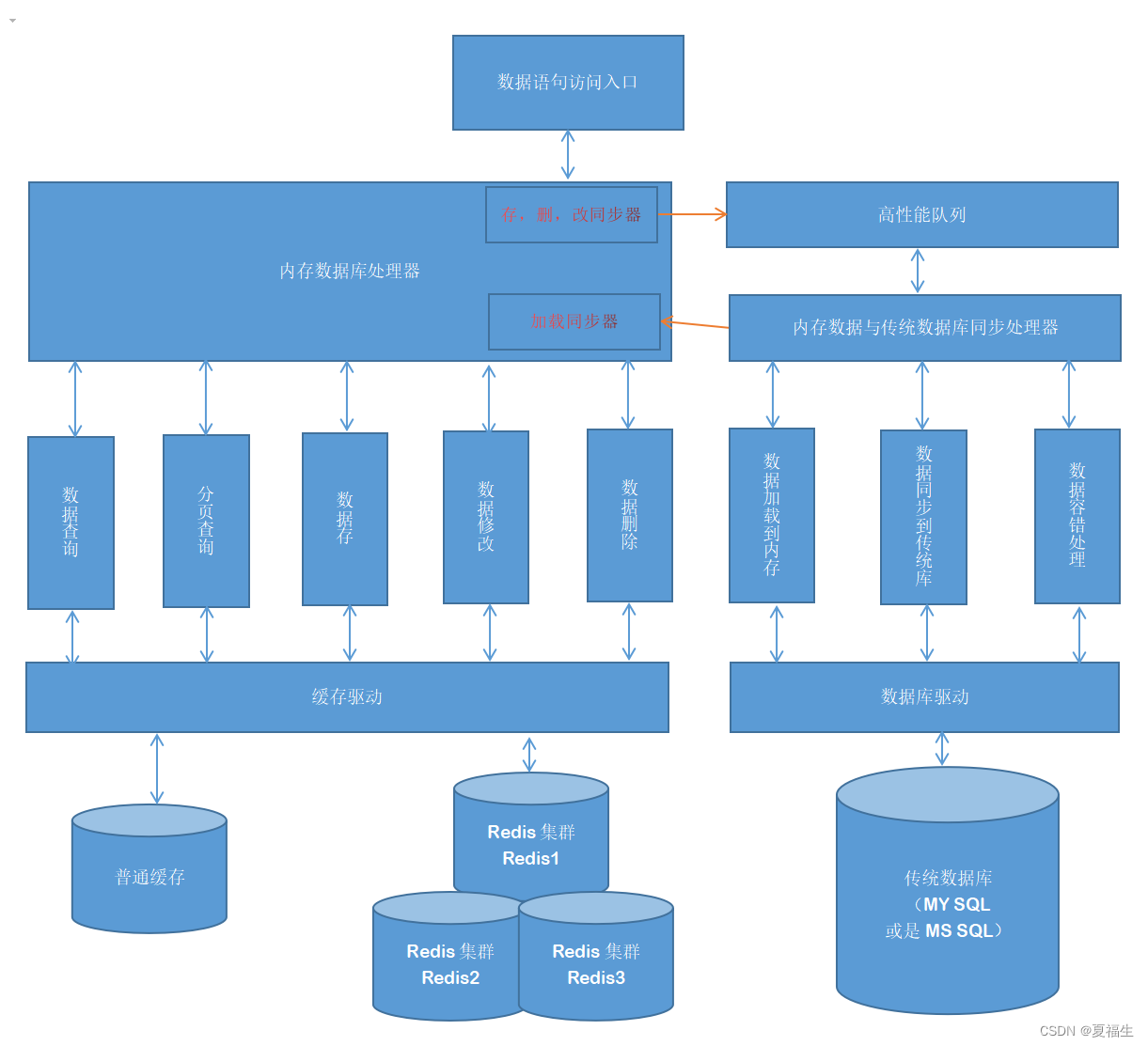
内存数据库的设计与实现(已在大型项目中应用)
一、概况 1、设计总图 组成,由Redis集群缓存,普通缓存,传统数据库,各类数据驱动 2、内存数据库的增删改查,分页查询 组成,由数据查询,分页查询,数据存储,数据修改,数据删除 3、内存数据库的驱动 组成,由驱动适配器,普通缓存驱动,Redis缓存驱动 4、内存数据库与…...

Linux基础命令-stat显示文件的状态信息
文章目录 stat 命令介绍 语法格式 基本参数 测试三个时间的变化过程 1)使用cat命令 2)使用echo命令 3)使用chmod命令 4)使用vim命令 参考实例 1)显示文件的状态信息 2)以简洁的形式显示状态信…...
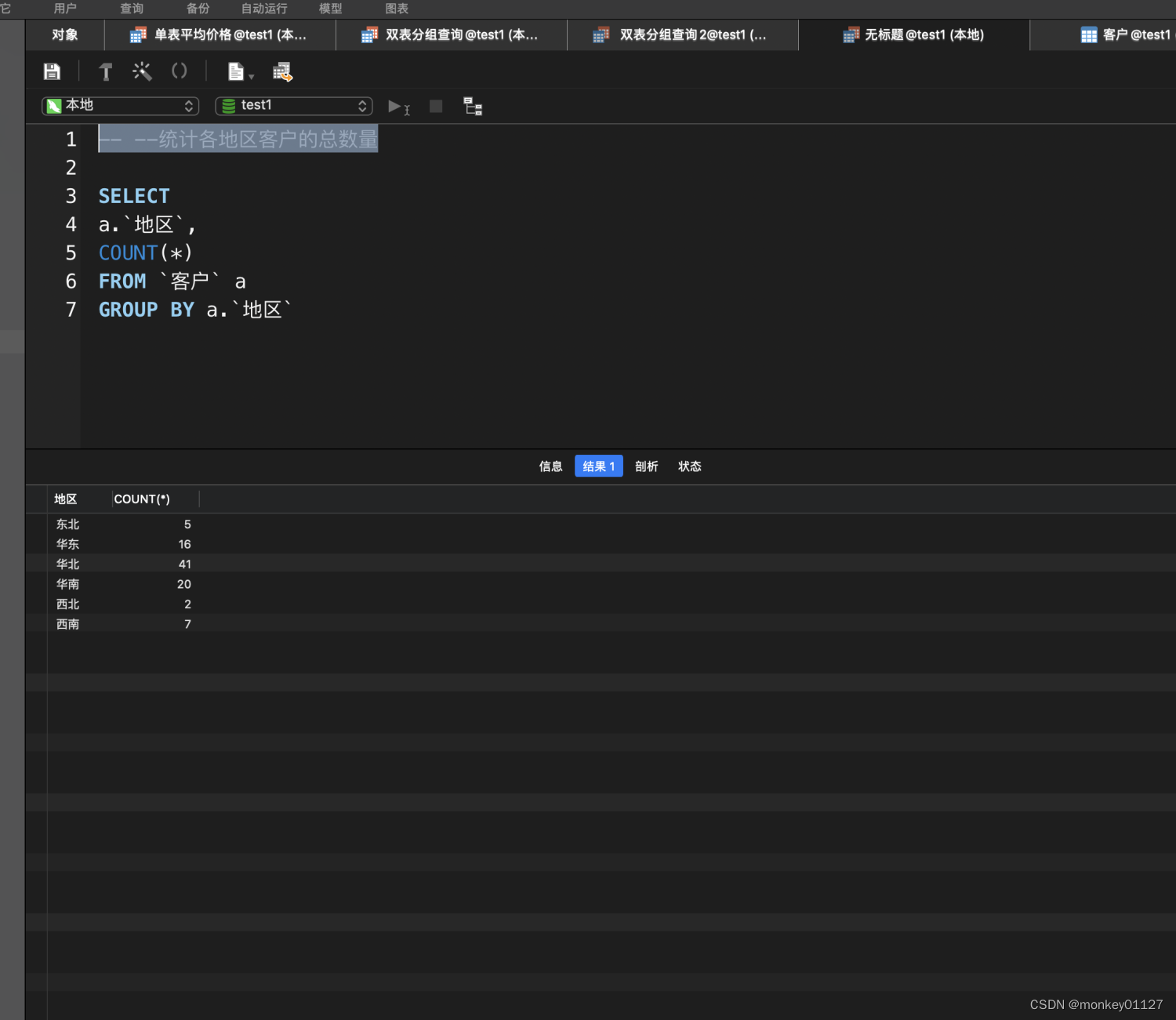
SQL入门DEMO
单表查询 ● --查询订购日期在1996年7月1日至1996年7月15日之间的订单的订购日期、订单ID、客户ID和雇员ID等字段的值 ● --查询供应商的ID、公司名称、地区、城市和电话字段的值。条件是“地区等于华北”并且“联系人头衔等于销售代表”。 –查询供应商的ID、公司名称、地…...

辉光管时钟学习制作及开源软硬件工程
文章目录前言开源地址辉光管项目介绍辉光管的工作条件硬件部分部分介绍充电电路驱动电路不足之处软件部分总结前言 作为一个电子人,一直想做一个辉光管时钟,算是大学的一个心愿,终于在快要毕业前做了一个,下面把软件和硬件的部分…...

动手学深度学习(第二版)学习笔记 第三章
第三章 线性神经网络 代码:d2l-zh/pytorch/chapter_linear-networks 3.1 线性回归 3.1. 线性回归 — 动手学深度学习 2.0.0 documentation 解析解 线性回归的解可以用一个公式简单地表达出来,这类解叫作解析解(analytical solution&…...
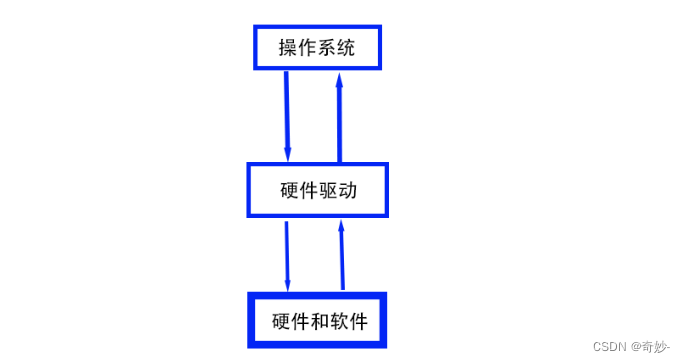
冯诺依曼体系结构与操作系统的概念及理解
一、 冯诺依曼体系结构1、概念2、内存的作用3、硬件原理解释软件行为二、操作系统的概念及基本作用1、概念2、设计操作系统的目的3、操作系统的主要作用4、什么是管理5、管理的目的6、操作系统如何为我们服务一、 冯诺依曼体系结构 我们常见的计算机,如笔记本。我们…...

【深度探讨】如何利用区块链改善公共服务
发表时间:2022年5月4日 信息来源:bsvblockchain.org BSV区块链协会全力支持符合企业和政府对于节能降耗和合法合规等相关要求的区块链生态系统。 然而,虽然监管机构负责其监管范围内的技术服务的性质、目的和影响,但他们并不是全…...

【打卡】图分析与节点嵌入
背景介绍 图(Graphs)是一种对物体(objects)和他们之间的关系(relationships)建模的数据结构,物体以结点(nodes)表示,关系以边(edges)…...
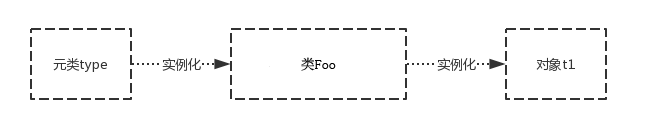
python元编程详解
什么是元编程 软件开发中很重要的一条原则就是“不要重复自己的工作(Don’t repeat youself)”,也就是说当我们需要复制粘贴代码时候,通常都需要寻找一个更加优雅的解决方案,在python中,这类问题常常会归类…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
