【Codeforces Round #853 (Div. 2)】C. Serval and Toxel‘s Arrays【题解】
题目
Toxel likes arrays. Before traveling to the Paldea region, Serval gave him an array aaa as a gift. This array has nnn pairwise distinct elements.
In order to get more arrays, Toxel performed mmm operations with the initial array. In the iii-th operation, he modified the pi-th element of the (i−1i−1i−1)-th array to viv_{i}vi, resulting in the iii-th array (the initial array a is numbered as 000). During modifications, Toxel guaranteed that the elements of each array are still pairwise distinct after each operation.
Finally, Toxel got m+1m+1m+1 arrays and denoted them as A0=a,A1,…,AmA_{0}=a,A_{1},…,A_{m}A0=a,A1,…,Am. For each pair (i,j)(0≤i<j≤m)(i,j) (0≤i<j≤m)(i,j)(0≤i<j≤m), Toxel defines its value as the number of distinct elements of the concatenation of AiA_{i}Ai and AjA_{j}Aj. Now Toxel wonders, what is the sum of the values of all pairs? Please help him to calculate the answer.
It is guaranteed that the sum of nnn and the sum of mmm over all test cases do not exceed 2⋅1052⋅10^{5}2⋅105.
思路
①初始化所有在原始数组中的数的数量为m+1m+1m+1。因为一共有m+1m+1m+1个数组,那么我一开始假定所有数组都与原始数组保持相同。
②对于第i(0≤i<m)i(0≤i<m)i(0≤i<m)个数组,也就是给出一个位置的修改,那么这个位置上原来的数对应的数量就要相应地减少m−im-im−i,因为在当前包括后面一共m−im-im−i个数组中这个位置上的数都要修改,并将其变成vvv,然后vvv的数量相应地增加m−im-im−i。这样,我们就统计出了这m+1m+1m+1个数组中所有不同的数分别出现的次数。
③现在统计这m+1m+1m+1个数组中不同的数分别对答案产生的贡献之和。设某个数的数量是cntcntcnt,那么含有这个数的cntcntcnt个数组与其它m+1−cntm+1-cntm+1−cnt个数组组合时这个数产生的贡献是cnt∗(m+1−cnt)cnt*(m+1-cnt)cnt∗(m+1−cnt);此外,含有这个数的cntcntcnt个数组两两组合时产生的Ccnt2=cnt∗(cnt−1)/2C^{2}_{cnt}=cnt*(cnt-1)/2Ccnt2=cnt∗(cnt−1)/2个组合分别产生了111的贡献。因此,答案就是:
ans=∑1n+m(cnt[i]∗(m+1−cnt[i])+cnt[i]∗(cnt[i]−1)/2)ans = \sum^{n+m}_{1}(cnt[i]*(m+1-cnt[i])+cnt[i]*(cnt[i]-1)/2)ans=∑1n+m(cnt[i]∗(m+1−cnt[i])+cnt[i]∗(cnt[i]−1)/2)。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn = 2e5+5;
ll n,m,a[maxn],cnt[maxn<<1];
void solve(){cin>>n>>m;memset(cnt,0,sizeof(cnt));for(ll i=1;i<=n;i++)cin>>a[i], cnt[a[i]] = m+1;for(ll i=0;i<m;i++){ll p,v;cin>>p>>v;cnt[a[p]] -= (m-i);a[p] = v;cnt[v] += (m-i);}ll ans = 0;for(ll i=1;i<=n+m;i++){if(cnt[i]==0)continue;ans += cnt[i]*(m+1-cnt[i]);ans += cnt[i]*(cnt[i]-1)/2;}cout<<ans<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);ll tests;cin>>tests;while(tests--){solve();}return 0;
}
相关文章:
】C. Serval and Toxel‘s Arrays【题解】)
【Codeforces Round #853 (Div. 2)】C. Serval and Toxel‘s Arrays【题解】
题目 Toxel likes arrays. Before traveling to the Paldea region, Serval gave him an array aaa as a gift. This array has nnn pairwise distinct elements. In order to get more arrays, Toxel performed mmm operations with the initial array. In the iii-th opera…...
100天精通Python(数据可视化篇)——第77天:数据可视化入门基础大全(万字总结+含常用图表动图展示)
文章目录1. 什么是数据可视化?2. 为什么会用数据可视化?3. 数据可视化的好处?4. 如何使用数据可视化?5. Python数据可视化常用工具1)Matplotlib绘图2)Seaborn绘图3)Bokeh绘图6. 常用图表介绍及其…...

PMP考前冲刺2.27 | 2023新征程,一举拿证
题目1-2:1.在产品开发过程中,项目发起人向项目团队推荐了一种新材料,新材料比现有的材料更便宜而且性能更好。如果团队采用新材料,不但有利于提升产品质量,而且可以显著降低成本。项目经理应该怎么办?A.采用新材料&am…...
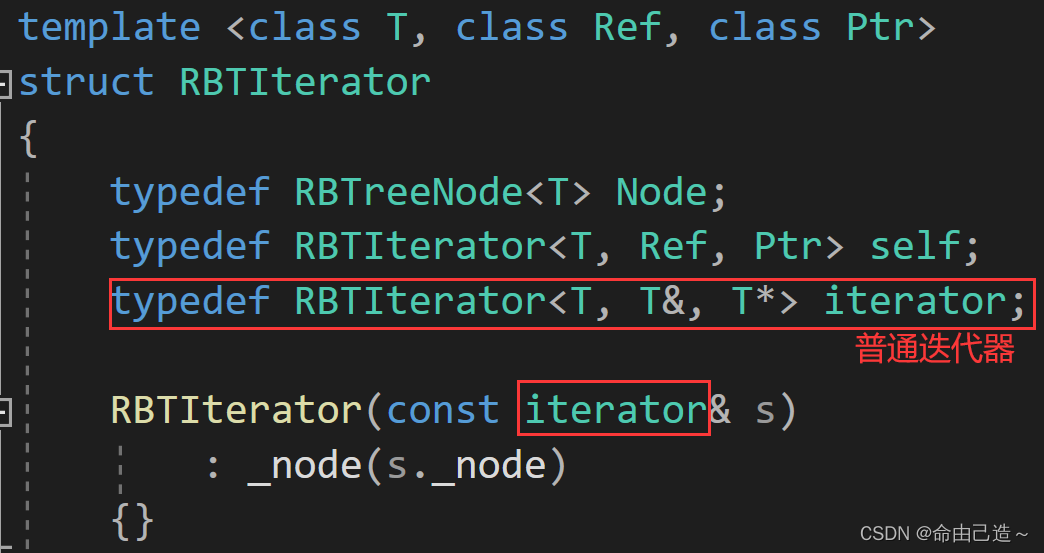
【C++】map和set的封装(红黑树)
map和set的封装一、介绍二、stl源码剖析三、仿函数获取数值四、红黑树的迭代器五、map的[]5.1 普通迭代器转const迭代器六、set源码七、map源码八、红黑树源码一、介绍 首先要知道map和set的底层都是用红黑树实现的 【数据结构】红黑树 set只需要一个key,但是map既…...
命令move)
【批处理脚本】-1.14-移动文件(夹)命令move
"><--点击返回「批处理BAT从入门到精通」总目录--> 共10页精讲(列举了所有move的用法,图文并茂,通俗易懂) 在从事“嵌入式软件开发”和“Autosar工具开发软件”过程中,经常会在其集成开发环境IDE(CodeWarrior,S32K DS,Davinci,EB Tresos,ETAS…)中,…...
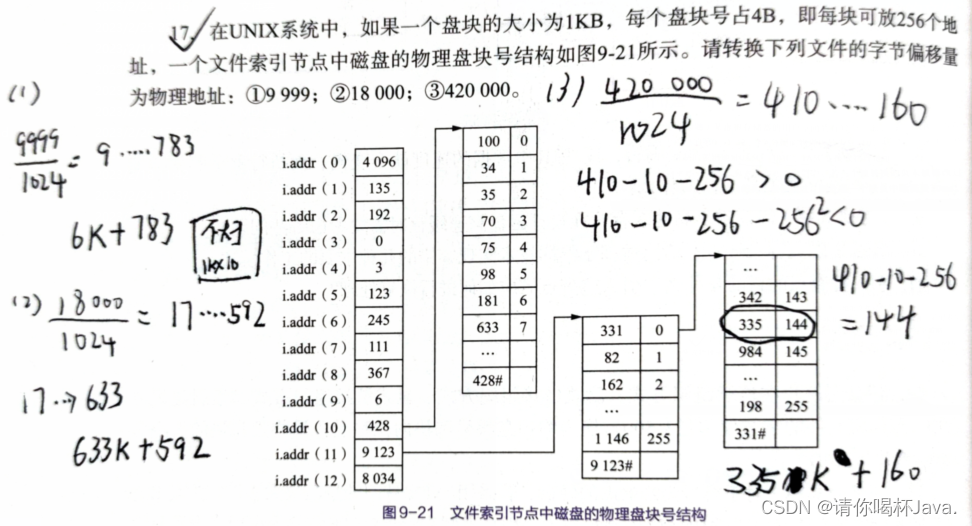
逻辑地址和物理地址转换
在操作系统的学习中,很多抵挡都会涉及虚拟地址转换为物理地址的计算,本篇就简单介绍一下在分页存储管理、分段存储管理、磁盘存储管理中涉及的地址转换问题。 虚拟地址与物理地址 编程一般只有可能和逻辑地址打交道,比如在 C 语言中&#x…...
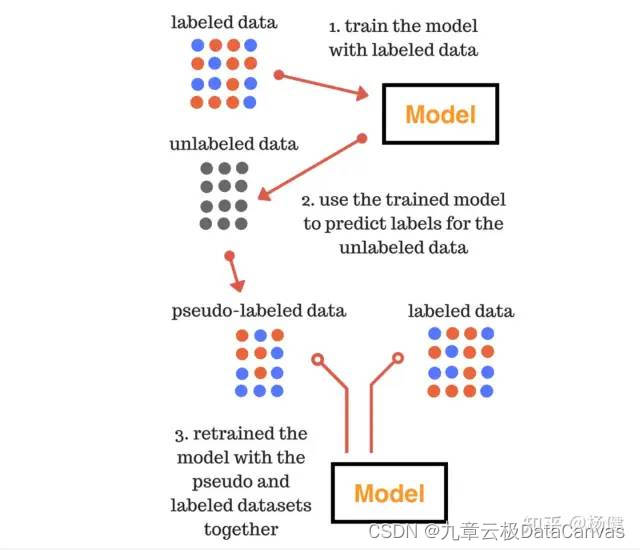
HyperGBM用4记组合拳提升AutoML模型泛化能力
本文作者:杨健,九章云极 DataCanvas 主任架构师 如何有效提高模型的泛化能力,始终是机器学习领域的重要课题。经过大量的实践证明比较有效的方式包括: 利用Early Stopping防止过拟合通过正则化降低模型的复杂度使用更多的训练数…...

P6软件中的前锋线设置
卷首语 所谓前锋线,是指从评估时刻的时标点出发,用点划线一次连接各项活动的实际进展位置所形成的的线段,其通常为折线。 关键路径法 前锋线比较法,是通过在进度计划中绘制实际进度前锋线以判断活动实际进度与计划进度的偏差&a…...

Spring Boot + Vue3 前后端分离 实战 wiki 知识库系统<二>---后端架构完善与接口开发
数据库准备: 在上一次Spring Boot Vue3 前后端分离 实战 wiki 知识库系统<一>---Spring Boot项目搭建已经将SpringBoot相关的配置环境给搭建好了,接下来则需要为咱们的项目创建一个数据库。 1、mysql的安装: 关于mysql的安装这里就…...
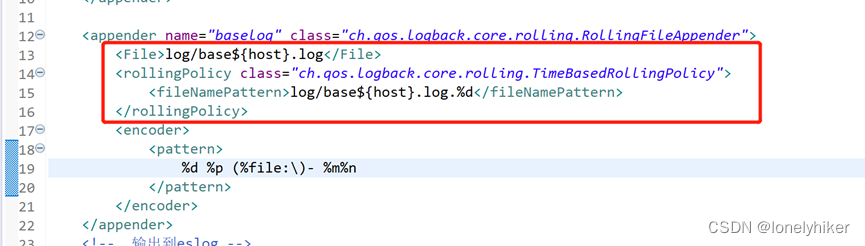
如何在logback.xml中自定义动态属性
原文地址:http://blog.jboost.cn/trick-logback-prop.html 当使用logback来记录Web应用的日志时,我们通过在logback.xml中配置appender来指定日志输出格式及输出文件路径,这在一台主机或一个文件系统上部署单个实例没有问题,但是…...
嵌入式系统硬件设计与实践(第一步下载eda软件)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 现实生活中,我们经常发现有的人定了很多的目标,但是到最后一个都没有实现。这听上去有点奇怪,但确实是实实在在…...
Portraiture4免费磨皮插件支持PS/LR
Portraiture 4免去了繁琐的手工劳动,选择性的屏蔽和由像素的平滑,以帮助您实现卓越的肖像润色。智能平滑,并删除不完善之处,同时保持皮肤的纹理和其他重要肖像的细节,如头发,眉毛,睫毛等。 一键…...

Python学习笔记202302
1、numpy.empty 作用:根据给定的维度和数值类型返回一个新的数组,其元素不进行初始化。 用法:numpy.empty(shape, dtypefloat, order‘C’) 2、logging.debug 作用:Python 的日志记录工具,这个模块为应用与库实现了灵…...

2023年大数据面试开胃菜
1、kafka的message包括哪些信息一个Kafka的Message由一个固定长度的header和一个变长的消息体body组成,header部分由一个字节的magic(文件格式)和四个字节的CRC32(用于判断body消息体是否正常)构成。当magic的值为1的时候,会在magic和crc32之间多一个字节…...

优雅的controller层设计
controller层设计 Controller 层逻辑 MVC架构下,我们的web工程结构会分为三层,自下而上是dao层,service层和controller层。controller层为控制层,主要处理外部请求。调用service层,一般情况下,contro…...

同步、通信、死锁
基础概念竞争资源引起两个问题死锁:因资源竞争陷入永远等待的状态饥饿:一个可运行程序由于其他进程总是优先于它,而被调用程序总是无限期地拖延而不能执行进程互斥:若干进程因相互争夺独占型资源而产生的竞争关系进程同步…...
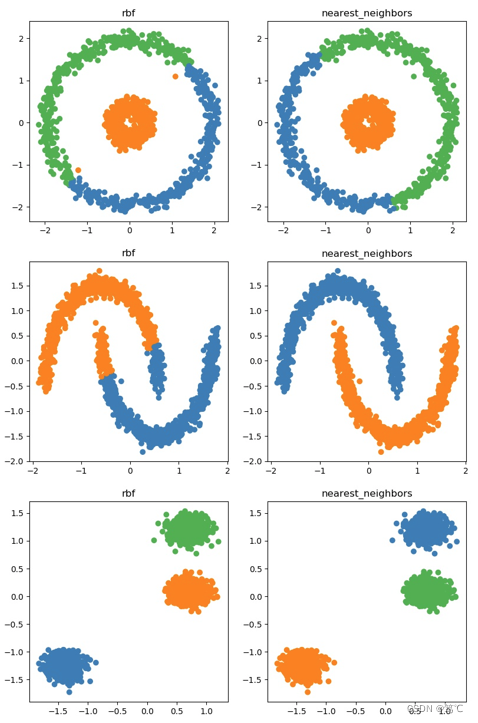
【聚类】谱聚类解读、代码示例
【聚类】谱聚类详解、代码示例 文章目录【聚类】谱聚类详解、代码示例1. 介绍2. 方法解读2.1 先验知识2.1.1 无向权重图2.1.2 拉普拉斯矩阵2.2 构建图(第一步)2.2.1 ϵ\epsilonϵ 邻近法2.2.2 k 近邻法2.2.3 全连接法2.3 切图(第二步…...
,简介)
最牛逼的垃圾回收期ZGC(1),简介
1丶什么是ZGC? ZGC是JDK 11中引入的一种可扩展的、低延迟的垃圾收集器。ZGC最主要的特点是:在非常短的时间内(一般不到10ms),就可以完成一次垃圾回收,而且这个时间是与堆的大小无关的。另外,ZGC支持非常大…...

微服务的Feign到底是什么
Feign是什么 分区是一种数据库优化技术,它可以将大表按照一定的规则分成多个小表,从而提高查询和维护的效率。在分区的过程中,数据库会将数据按照分区规则分配到不同的分区中,并且可以在分区中使用索引和其他优化技术来提高查询效…...

JavaScript 正则表达式
正则表达式(英语:Regular Expression,在代码中常简写为regex、regexp或RE)使用单个字符串来描述、匹配一系列符合某个句法规则的字符串搜索模式。搜索模式可用于文本搜索和文本替换。什么是正则表达式?正则表达式是由一…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
