「牛客网C」初学者入门训练BC156
🐶博主主页:@ᰔᩚ. 一怀明月ꦿ
❤️🔥专栏系列:线性代数,C初学者入门训练
🔥座右铭:“不要等到什么都没有了,才下定决心去做”
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
题目:BC156 牛牛的数组匹配
描述:
牛牛刚学会数组不久,他拿到两个数组 a 和 b,询问 b 的哪一段连续子数组之和与数组 a 之和最接近。 如果有多个子数组之和同样接近,输出起始点最靠左的数组。
输入描述:
第一行输入两个正整数 n 和 m ,表示数组 a 和 b 的长度。
第二第三行输入 n 个和 m 个正整数,表示数组中 a 和 b 的值。
输出描述:
输出子数组之和最接近 a 的子数组
示例1
输入:
2 6 30 39 15 29 42 1 44 1 输出: 29 42示例2
输入:
6 1 50 47 24 19 46 47 2 输出: 2解题思路:询问 b 的哪一段连续子数组之和与数组 a 之和最接近,我们可以先计算每一个b数组元素b[i]与数组 a 之和sum的差值绝对值,然后记录差值,和此时的坐标,然后分别计算b[i]+b[i+1],b[i]+b[i+1]+b[i+2],b[i]+b[i+1]+b[i+2]+...+b[m]和sum的差值绝对值,然后分别记录差值,和此时的坐标。最后按照起始和末尾坐标打印。
解题详细过程:
#include<stdio.h> int Abs(int sum1,int sum2) {if(sum1>sum2)return sum1-sum2;return sum2-sum1; } void Fun(int sum1,int b[],int m)//Fun这个函数就是完成“询问 b 的哪一段连续子数组之和与数组 a 之和最接近”这个功能。 {int i=0,j=0,S=0,E=0;//S就是记录起始的位置,E记录末尾的位置int sum2=0;int min=sum1;//min记录sum2和sum1的差值绝对值,但是初始化为a数组之和for(i=0;i<m;i++){sum2=b[i];for(j=i+1;j<=m;j++){if(Abs(sum1,sum2)<min){min=Abs(sum1,sum2);S=i;E=j;}sum2+=b[j];}}for(i=S;i<E;i++)//打印{printf("%d ",b[i]);}printf("\n"); } int main() {printf("请输入a数组的长度,b数组的长度\n");int n=0,m=0;scanf("%d %d",&n,&m);int a[n];int b[m];printf("请输入a数组\n");int i=0;int sum=0;//统计b数组的和for(i=0;i<n;i++){scanf("%d",&a[i]);sum+=a[i];}printf("请输入b数组\n");for(i=0;i<m;i++){scanf("%d",&b[i]);}Fun(sum,b,m);return 0; }关于这个Abs函数我想重点叙述一下
int Abs(int sum1,int sum2) {if(sum1>sum2)return sum1-sum2;return sum2-sum1;Abs就是absolute value(绝对值)缩写,这里计算两个数的差值的绝对值,但注意,因为有人就会想我直接把这两个数定义为无符号整形,再以无符号整形打印,不一样可以得到绝对值吗,如果这样想就错了,无符号整形型的数的二进制是没有符号位的,所以原码,反码,补码,转换是有所差异的,例如-1无符号数是一个很大的数,而不是1
🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸
相关文章:

「牛客网C」初学者入门训练BC156
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练 🔥座右铭:“不要等到什么都没有了,才下定决心去做” 🚀🚀🚀大家觉不错…...
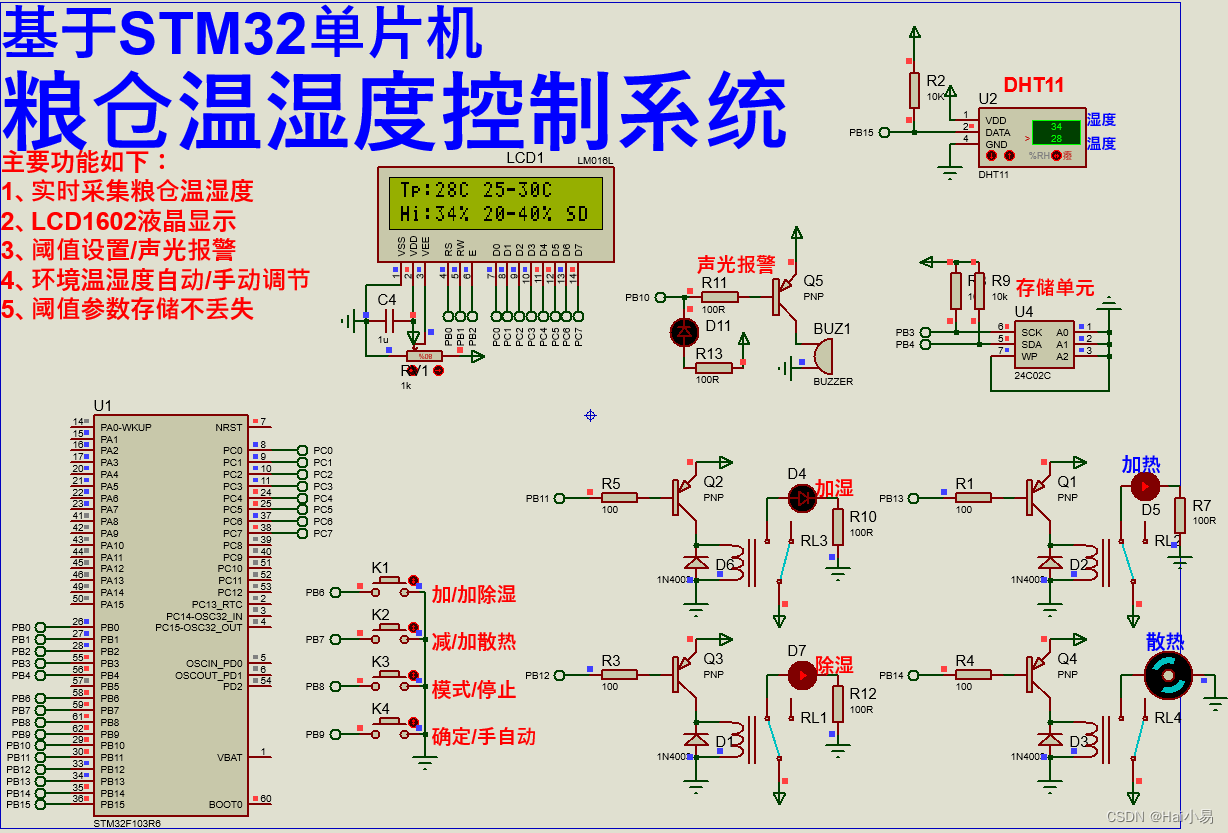
【Proteus仿真】【STM32单片机】粮仓温湿度控制系统设计
文章目录一、功能简介二、软件设计三、实验现象联系作者一、功能简介 本项目使用Proteus8仿真STM32单片机控制器,使用声光报警模块、LCD1602显示模块、DHT11温湿度模块、继电器模块、加热加湿除湿风扇等。 主要功能: 系统运行后,LCD1602显示…...

九年时间,倾情投入,JumpServer开源堡垒机v3.0正式发布
2023年2月27日,JumpServer开源堡垒机正式发布v3.0版本。在JumpServer开源堡垒机v3.0版本的设计过程中,我们始终秉持着“内外兼修”的原则,旨在进一步提升用户的使用体验,真正用心做好一款开源堡垒机。 在JumpServer v3.0版本中&…...

【ROS学习笔记5】服务通信
【ROS学习笔记5】服务通信 文章目录【ROS学习笔记5】服务通信前言一、服务通信的理论模型二、服务通信自定义srv三、服务通信自定义srv的Cpp实现四、服务通信自定义srv的Python实现五、Reference写在前面,本系列笔记参考的是AutoLabor的教程,具体项目地址…...
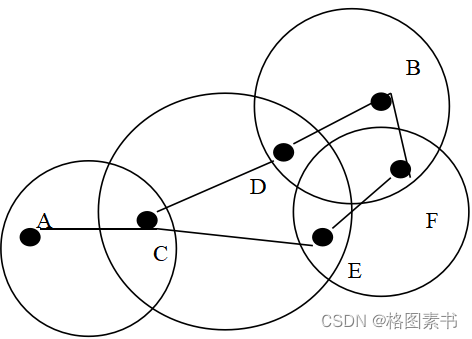
“华为杯”研究生数学建模竞赛2006年-【华为杯】A题:Ad Hoc 网络中的区域划分和资源分配问题(附获奖论文)
赛题描述 Ad Hoc网络是当前网络和通信技术研究的热点之一,对于诸如军队和在野外作业的大型公司和集团来说,Ad Hoc网络有着无需基站、无需特定交换和路由节点、随机组建、灵活接入、移动方便等特点,因而具有极大的吸引力。 在Ad Hoc网络中,节点之间的通信均通过无线传输来完…...

编写第一个JAVA程序,常见踩坑记录
编写第一个JAVA程序 预备环境 电脑需要安装JDK 及 配置环境变量打开cmd 输入java -version 能运行在说 创建工程 创建文件夹javaCode(随意叫…) 创建文件Hello.java 编写代码 public class Hello{public static void main(String[] args){System.out.print("hello wo…...

求职陷阱:Lazarus组织以日本瑞穗銀行等招聘信息为诱饵的攻击活动分析
概述 Lazarus组织是疑似具有东北亚背景的APT组织,奇安信威胁情报中心内部追踪编号为APT-Q-1,因2014年攻击索尼影业开始受到广泛关注,其攻击活动最早可追溯到2007年。该组织早期主要针对其他国家政府机构,以窃取敏感情报为目的&am…...

【C语言每日一题】判断字符串旋转结果(附加字符串左旋详解)
【C语言每日一题】—— 判断字符串旋转结果😎😎😎 目录 💡前言🌞: 💛字符串左旋题目💛 💪 解题思路的分享💪 😊题目源码的分享…...

SpringSecurity+JWT+Redis进行用户鉴权和接口权限的控制
系统的登录,都做些什么?用户访问登录页时:会发起一个获取图片验证码的请求,后端先生成一个uuid代表此次的验证码,接着生成 "ab?答案" 的表达式,将前面的内容转换成流生成图片,后面的答案则存储到…...

七大排序(Java)
目录 一、插入排序 1. 直接插入排序 2. 希尔排序 二、选择排序 1. 直接选择排序 2. 堆排序 三、交换排序 1. 冒泡排序 2. 快速排序 四、归并排序 五、总结 一、插入排序 1. 直接插入排序 抓一张牌,在有序的牌中,找到合适的位置并且插入。 时间…...

分享一些可以快速掌握python语法的小技巧
下面是我总结的一些有助于快速掌握 Python 语法的小技巧,欢迎一起交流。 注释:在代码中添加注释可以帮助你和其他人理解代码的目的和功能。在 Python 中,使用 # 符号来添加单行注释,使用三引号 """ 或 来添加多行…...
1.FFmpeg-音视频基础
专栏介绍基于最新的FFmpeg5.1.2版本讲解学习, 跟随博主一起学习ffmpeg: 本专栏学习流程为: FFmpeg安装、...
Parasoft的自动化测试平台到底强在哪?
在如今产品迭代如此之快的大背景下,软件测试这项工作越来越被大家所重视,但是通常情况下大家都是选择在产品上线前再去做测试,这个时候就会面临很多麻烦和挑战。首先,产品已经开发好之后,体量比较大,要从哪…...
FastDDS-0.简介
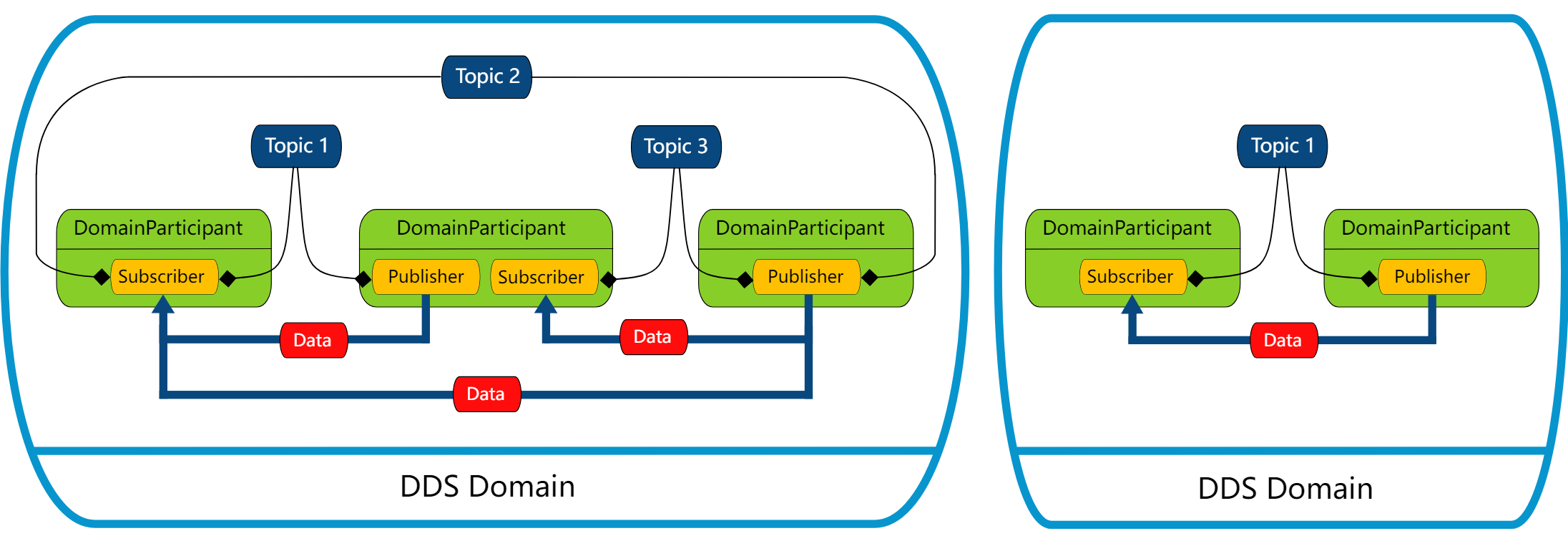
FastDDS简介 eProsima Fast DDS 是 DDS (Data Distribution Service) 协议的一个C语言实现版本,该协议由 Object Management Group (OMG) 组织定义。 eProsima Fast DDS 库既提供了一个应用编程接口(API),又提供了一种通信协议&a…...
Flutter入门进阶之旅 -开源Flutter项目
开源Flutter项目 该项目为纯flutter端项目,采用aar方式寄生在原生APP中,作为APP中的一个独立模块 在业务逻辑上做到与原生APP完全隔离,Flutter端开发者,可完全不用关注原生端的业务模块 两端开发彼此业务隔离,缩小了对…...
Opencv项目实战:21 美国ASL手势识别
0、项目介绍 首先,我可以保证在这里,你并不需要多么了解深的机器学习算法,我的初衷是通过本项目,激发大家学习机器学习的动力。选择这种手势原因是因为只有24个字母,你的电脑足以带的动,虽然我只训练A、B、…...

强化学习RL 01: Reinforcement Learning 基础
目录 RL理解要点 1. RL数学基础 1.1 Random Variable 随机变量 1.2 概率密度函数 Probability Density Function(PDF) 1.3 期望 Expectation 1.4 随机抽样 Random Sampling 2. RL术语 Terminologies 2.1 agent、state 和 action 2.2 策略 policy π 2.3 奖励 reward …...

C语言之练习题合集
💗 💗 博客:小怡同学 💗 💗 个人简介:编程小萌新 💗 💗 如果博客对大家有用的话,请点赞关注再收藏 🌞 文章目录leetcode 题号:728. 自除数leetcode 题号:238.…...
sublimeText3新建文件自动添加注释头
参考: https://github.com/shiyanhui/FileHeader/blob/master/README.rst https://packagecontrol.io/packages/FileHeader https://github.com/shiyanhui/FileHeader fileheader:https://codeload.github.com/shiyanhui/FileHeader/zip/refs/heads/m…...

AndroidStudio打包HBuilderX的H5+项目为安卓App【一次过,无任何异常报错】
目录 1.查看HBuilderX的版本号 2.下载Dcloud上对应的安卓SDK 3.下载完安卓SDK后,我们解压它,注意不要放在任何有中文组成的文件夹中【是否有中文决定于你鼠标单击上面路径后,第一张图还没鼠标单击,第二张已鼠标单击,…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
