第十四届蓝桥杯第三期官方模拟赛C\C++题解
文章目录
- A-填空题
- 题意
- 算法
- 参考代码(C++)
- B-填空题
- 题意
- 算法
- 参考代码(C++)
- C-填空题
- 题意
- 算法
- 参考代码(C++)
- D-填空题
- 题意
- 算法
- 参考代码(C++)
- E-填空题
- 题意
- 算法
- 参考代码(C++)
- F
- 题意
- 算法
- 参考代码(C++)
- G
- 题意
- 算法
- 参考代码(C++)
- H
- 题意
- 算法
- 参考代码(C++)
- I
- 题意
- 算法
- 参考代码(C++)
- J
- 题意
- 算法
- 参考代码(C++)
A-填空题
题意
请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。请将这个数的十进制形式作为答案提交。
算法
答案:2730。
模拟即可。
参考代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;bool check(int x) {while(x) {if(x % 16 >= 10 && x % 16 <= 15) ;else {return false;}x /= 16;}return true;
}int main() {for(int i = 2023; ; i ++) {if(check(i)) {cout << i << "\n";break;}}return 0;
}
B-填空题
题意
在 Excel 中,列的名称使用英文字母的组合。前 26 列用一个字母,依次为 A 到 Z,接下来 26*26 列使用两个字母的组合,依次为 AA 到 ZZ。请问第 2022 列的名称是什么?
算法
答案:BYT。
由于2022比较小,最多只需要三位就可以表示出来,因为三位可以表示的最大值为26326^3263远大于2022。这道题的原题是codefroces上的一道题,那题的数据量非常大,需要在普通的进制转换上增加几行代码,不过本题只需要暴力枚举即可。
参考代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int get(int x, int y, int z) {return x * 26 * 26 + y * 26 + z;
}string ans(int x, int y, int z) {string s;s += 'A' + x - 1;s += 'A' + y - 1;s += 'A' + z - 1;return s;
}int main() {int n = 2022;for(int i = 1; i <= 26; i ++)for(int j = 1; j <= 26; j ++)for(int k = 1; k <= 26; k ++)if(get(i, j, k) == n) {cout << ans(i, j, k) << "\n";return 0;}return 0;
}
C-填空题
题意
对于一个日期,我们可以计算出年份的各个数位上的数字之和,也可以分别计算月和日的各位数字之和。请问从 1900 年 1 月 1 日至 9999 年 12 月 31 日,总共有多少天,年份的数位数字之和等于月的数位数字之和加日的数位数字之和。
例如,2022年11月13日满足要求,因为 2+0+2+2=(1+1)+(1+3) 。请提交满足条件的日期的总数量。
算法
答案:43898。
枚举1900到9999中的每一年,对于一个特定的年份,我们枚举它的每一天即可,具体就是先枚举当前年的月份,再枚举当前月的天数,需要注意的是,如果当前枚举的年份是闰年,那当我们枚举的月份是2月时,对应的2月份天数是29天。
参考代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int days[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30};bool is_leap(int year) {return (year % 4 == 0 && year % 100 != 0) || (year % 400 == 0);
}int get(int x) {int res = 0;while(x) {res += x % 10;x /= 10;}return res;
}int work(int y, bool leap) {int cnt = 0;for(int i = 1; i <= 12; i ++) {int k = days[i];if(k == 2 && leap) k ++ ;for(int j = 1; j <= k; j ++) {if(get(y) == get(i) + get(k)) {cnt ++ ;}}}return cnt;
}int main() {int res = 0;for(int y = 1900; y <= 9999; y ++) {bool leapY = is_leap(y);res += work(y, leapY);}cout << res << "\n";return 0;
}
D-填空题
题意
小蓝有 30 个数,分别为:99, 22, 51, 63, 72, 61, 20, 88, 40, 21, 63, 30, 11, 18, 99, 12, 93, 16, 7, 53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77 。小蓝可以在这些数中取出两个序号不同的数,共有 30*29/2=435 种取法。请问这 435 种取法中,有多少种取法取出的两个数的乘积大于等于 2022 。
算法
答案:189。
枚举即可。
参考代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int nums[31] = {0, 99, 22, 51, 63, 72, 61, 20, 88, 40,21, 63, 30, 11, 18, 99, 12, 93, 16, 7, 53,64, 9, 28, 84, 34, 96, 52, 82, 51, 77};int main() {int res = 0;for(int i = 1; i <= 30; i ++)for(int j = i + 1; j <= 30; j ++) {if(nums[i] * nums[j] >= 2022) {res ++ ;}}cout << res << "\n";return 0;
}
E-填空题
题意
小蓝有一个 30 行 60 列的数字矩阵,矩阵中的每个数都是 0 或 1 。
110010000011111110101001001001101010111011011011101001111110
010000000001010001101100000010010110001111100010101100011110
001011101000100011111111111010000010010101010111001000010100
101100001101011101101011011001000110111111010000000110110000
010101100100010000111000100111100110001110111101010011001011
010011011010011110111101111001001001010111110001101000100011
101001011000110100001101011000000110110110100100110111101011
101111000000101000111001100010110000100110001001000101011001
001110111010001011110000001111100001010101001110011010101110
001010101000110001011111001010111111100110000011011111101010
011111100011001110100101001011110011000101011000100111001011
011010001101011110011011111010111110010100101000110111010110
001110000111100100101110001011101010001100010111110111011011
111100001000001100010110101100111001001111100100110000001101
001110010000000111011110000011000010101000111000000110101101
100100011101011111001101001010011111110010111101000010000111
110010100110101100001101111101010011000110101100000110001010
110101101100001110000100010001001010100010110100100001000011
100100000100001101010101001101000101101000000101111110001010
101101011010101000111110110000110100000010011111111100110010
101111000100000100011000010001011111001010010001010110001010
001010001110101010000100010011101001010101101101010111100101
001111110000101100010111111100000100101010000001011101100001
101011110010000010010110000100001010011111100011011000110010
011110010100011101100101111101000001011100001011010001110011
000101000101000010010010110111000010101111001101100110011100
100011100110011111000110011001111100001110110111001001000111
111011000110001000110111011001011110010010010110101000011111
011110011110110110011011001011010000100100101010110000010011
010011110011100101010101111010001001001111101111101110011101
如果从一个标为 1 的位置可以通过上下左右走到另一个标为 1 的位置,则称两个位置连通。与某一个标为 1 的位置连通的所有位置(包括自己)组成一个连通分块。请问矩阵中最大的连通分块有多大?
算法
答案:148。
flood-fill算法,本质是一个爆搜。
参考代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 35, M = 65;int n = 30, m = 60;
char g[N][M];int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};int dfs(int x, int y) {int cnt = 1;g[x][y] = '0';for(int d = 0; d < 4; d ++) {int a = x + dx[d], b = y + dy[d];if(a <= n && a >= 1 && b <= m && b >= 1 && g[a][b] == '1') {cnt += dfs(a, b);}}return cnt;
}int main() {int res = 0;for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++)cin >> g[i][j];for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++)if(g[i][j] == '1')res = max(res, dfs(i, j));cout << res << "\n";return 0;}
F
题意
给定一天是一周中的哪天,请问 n 天后是一周中的哪天?
输入第一行包含一个整数 w,表示给定的天是一周中的哪天,w 为 1 到 6 分别表示周一到周六,w 为 7 表示周日。第二行包含一个整数 n。
输出一行包含一个整数,表示 n 天后是一周中的哪天,1 到 6 分别表示周一到周六,7 表示周日。
对于所有评测用例,1 <= n <= 1000000。
算法
模拟即可。
参考代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int main() {int w, n;cin >> w >> n;while(n --) {w ++ ;if(w == 8) w = 1;}cout << w << "\n";return 0;
}
G
题意
小蓝负责一块区域的信号塔安装,整块区域是一个长方形区域,建立坐标轴后,西南角坐标为 (0, 0), 东南角坐标为 (W, 0), 西北角坐标为 (0, H), 东北角坐标为 (W, H)。其中 W, H 都是整数。
他在 n 个位置设置了信号塔,每个信号塔可以覆盖以自己为圆心,半径为 R 的圆形(包括边缘)。
为了对信号覆盖的情况进行检查,小蓝打算在区域内的所有横纵坐标为整数的点进行测试,检查信号状态。其中横坐标范围为 0 到 W,纵坐标范围为 0 到 H,总共测试 (W+1) * (H+1) 个点。
给定信号塔的位置,请问这 (W+1)*(H+1) 个点中有多少个点被信号覆盖。
输入第一行包含四个整数 W, H, n, R,相邻整数之间使用一个空格分隔。
接下来 n 行,每行包含两个整数 x, y,表示一个信号塔的坐标。信号塔可能重合,表示两个信号发射器装在了同一个位置。
输出一行包含一个整数,表示答案。
对于所有评测用例,1 <= W, H <= 100,1 <= n <= 100, 1 <= R <= 100, 0 <= x <= W, 0 <= y <= H。
算法
暴力枚举。判断一个点是否在一个圆内(包括圆上),只需要判断某点到圆的圆心的距离是否不大于圆的半径,由于计算机中开根号会导致精度丢失,所以我们转换为判断距离的平方是否不大于圆半径的平方即可。
参考代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>#define x first
#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 110;int w, h;
int n, R;
PII cs[N];int main() {cin >> w >> h >> n >> R;for(int i = 0; i < n; i ++) cin >> cs[i].x >> cs[i].y;int res = 0;for(int x = 0; x <= w; x ++)for(int y = 0; y <= h; y ++) {bool flag = false;for(int k = 0; k < n; k ++) {if((x - cs[k].x) * (x - cs[k].x) +(y - cs[k].y) * (y - cs[k].y) <= R * R) {flag = true;break;}}if(flag) res ++ ;}cout << res << "\n";return 0;
}
H
题意
小蓝有一个 n * m 大小的矩形水域,小蓝将这个水域划分为 n 行 m 列,行数从 1 到 n 标号,列数从 1 到 m 标号。每行和每列的宽度都是单位 1 。现在,这个水域长满了水草,小蓝要清理水草。每次,小蓝可以清理一块矩形的区域,从第 r1 行(含)到第 r2 行(含)的第 c1 列(含)到 c2 列(含)。经过一段时间清理后,请问还有多少地方没有被清理过。
输入第一行包含两个整数 n, m,用一个空格分隔。
第二行包含一个整数 t ,表示清理的次数。
接下来 t 行,每行四个整数 r1, c1, r2, c2,相邻整数之间用一个空格分隔,表示一次清理。请注意输入的顺序。
输出一行包含一个整数,表示没有被清理过的面积。
对于所有评测用例,1 <= r1 <= r2 <= n <= 100, 1 <= c1 <= c2 <= m <= 100, 0 <= t <= 100。
算法
暴力枚举所给出的区域内的点,将他们的状态标记为已经清理,不会超时,但是本题明显考察的是二维差分算法,而且二维差分相对来说更好写,选择使用二维差分。
参考代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110, M = 110;int n, m;
int g[N][M];void add(int x1, int y1, int x2, int y2, int c) {g[x1][y1] += c;g[x2 + 1][y1] -= c;g[x1][y2 + 1] -= c;g[x2 + 1][y2 + 1] += c;
}int main() {cin >> n >> m;int T;cin >> T;memset(g, 0, sizeof g);while(T -- ) {int l, r, d, u;cin >> l >> d >> r >> u; // markadd(l, d, r, u, 1);}for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++)g[i][j] += g[i - 1][j] + g[i][j - 1] - g[i - 1][j - 1];// for(int i = 1; i <= n; i ++) {
// for(int j = 1; j <= m; j ++)
// cout << g[i][j] << " ";
// cout << "\n";
// }int res = 0;for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++)if(!g[i][j])res ++ ;cout << res << "\n";return 0;
}
I
题意
小蓝准备在一个空旷的场地里面滑行,这个场地的高度不一,小蓝用一个 n 行 m 列的矩阵来表示场地,矩阵中的数值表示场地的高度。
如果小蓝在某个位置,而他上、下、左、右中有一个位置的高度(严格)低于当前的高度,小蓝就可以滑过去,滑动距离为 1 。
如果小蓝在某个位置,而他上、下、左、右中所有位置的高度都大于等于当前的高度,小蓝的滑行就结束了。
小蓝不能滑出矩阵所表示的场地。
小蓝可以任意选择一个位置开始滑行,请问小蓝最多能滑行多远距离。
输入第一行包含两个整数 n, m,用一个空格分隔。
接下来 n 行,每行包含 m 个整数,相邻整数之间用一个空格分隔,依次表示每个位置的高度。
输出一行包含一个整数,表示答案。
对于 30% 评测用例,1 <= n <= 20,1 <= m <= 20,0 <= 高度 <= 100。
对于所有评测用例,1 <= n <= 100,1 <= m <= 100,0 <= 高度 <= 10000。
算法
枚举起点,爆搜当前起点所对应的最长经过的点数,更新答案的最大值。这里需要吐槽一下官方,明明讲的是滑行长度,但是样例却是经过的点数,最终以样例为准。
参考代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110, M = 110;int n, m;
int g[N][M];
bool vis[N][N];int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};int dfs(int x, int y) {int dep = 0;for(int d = 0; d < 4; d ++) {int a = x + dx[d], b = y + dy[d];if(a >= 1 && a <= n && b >= 1 && b <= m && !vis[a][b] && g[x][y] > g[a][b]) {vis[a][b] = true;dep = max(dep, dfs(a, b) + 1);vis[a][b] = false;}}return dep;
}int main() {scanf("%d%d", &n, &m);int res = 0;for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++)scanf("%d", &g[i][j]);for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++) {memset(vis, 0, (n + 1) * (m + 1) * 4);vis[i][j] = true;res = max(res, dfs(i, j));vis[i][j] = false;}cout << res + 1 << "\n";return 0;
}
J
题意
小蓝有一个序列 a[1], a[2], …, a[n]。给定一个正整数 k,请问对于每一个 1 到 n 之间的序号 i,a[i-k], a[i-k+1], …, a[i+k] 这 2k+1 个数中的最小值是多少?当某个下标超过 1 到 n 的范围时,数不存在,求最小值时只取存在的那些值。
输入的第一行包含一整数 n。
第二行包含 n 个整数,分别表示 a[1], a[2], …, a[n]。
第三行包含一个整数 k 。
输出一行,包含 n 个整数,分别表示对于每个序号求得的最小值。
对于 30% 的评测用例,1 <= n <= 1000,1 <= a[i] <= 1000。
对于 50% 的评测用例,1 <= n <= 10000,1 <= a[i] <= 10000。
对于所有评测用例,1 <= n <= 1000000,1 <= a[i] <= 1000000。
算法
求解一个区间内最值的是一个非常经典的问题,自然对应着经典的写法,这里提供st表的示例代码,st表本质上是一个DP,算得上是求解这类问题的经典方法了,但是st比较死板,只能求解这类问题。如果想了解更多这类经典问题的解法,可以了解一下线段树。
参考代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;const int N = 1000010, M = 20;int n, k, t;
int q[N];
int f[N][M]; // min_valint query(int l, int r) {int len = log(r - l + 1) / log(2);int x = f[l][len], y = f[r - (1 << len) + 1][len];int res = 0;if(q[x] > q[y]) res = y;else res = x;return res;
}int main() {scanf("%d", &n);for(int i = 1; i <= n; i ++) scanf("%d", &q[i]);scanf("%d", &k);t = log(n) / log(2);for(int j = 0; j <= t; j ++) {for(int i = 1; i + (1 << j) - 1 <= n; i ++) {if(!j) f[i][j] = i;else {int l = f[i][j - 1], r = f[i + (1 << j - 1)][j - 1];if(q[l] > q[r]) f[i][j] = r;else f[i][j] = l;}}}int l, r;for(int i = 1; i <= n; i ++) {l = max(1, i - k), r = min(n, i + k);
// cout << l << " " << r << "\n";cout << q[query(l, r)] << " ";}cout << "\n";return 0;
}
相关文章:

第十四届蓝桥杯第三期官方模拟赛C\C++题解
文章目录A-填空题题意算法参考代码(C)B-填空题题意算法参考代码(C)C-填空题题意算法参考代码(C)D-填空题题意算法参考代码(C)E-填空题题意算法参考代码(C)F题…...

API接口安全
目前项目都是前后端分离或者有对外提供接口的需求,在这些情况下,就要考虑接口安全。 如果不重视接口安全,可能导致严重的危害,例如数据盗取,服务宕机等。 可能的安全问题: 1.明文密码被攻击者抓包看到 前端可对密码或…...
2023前端一面vue面试题合集
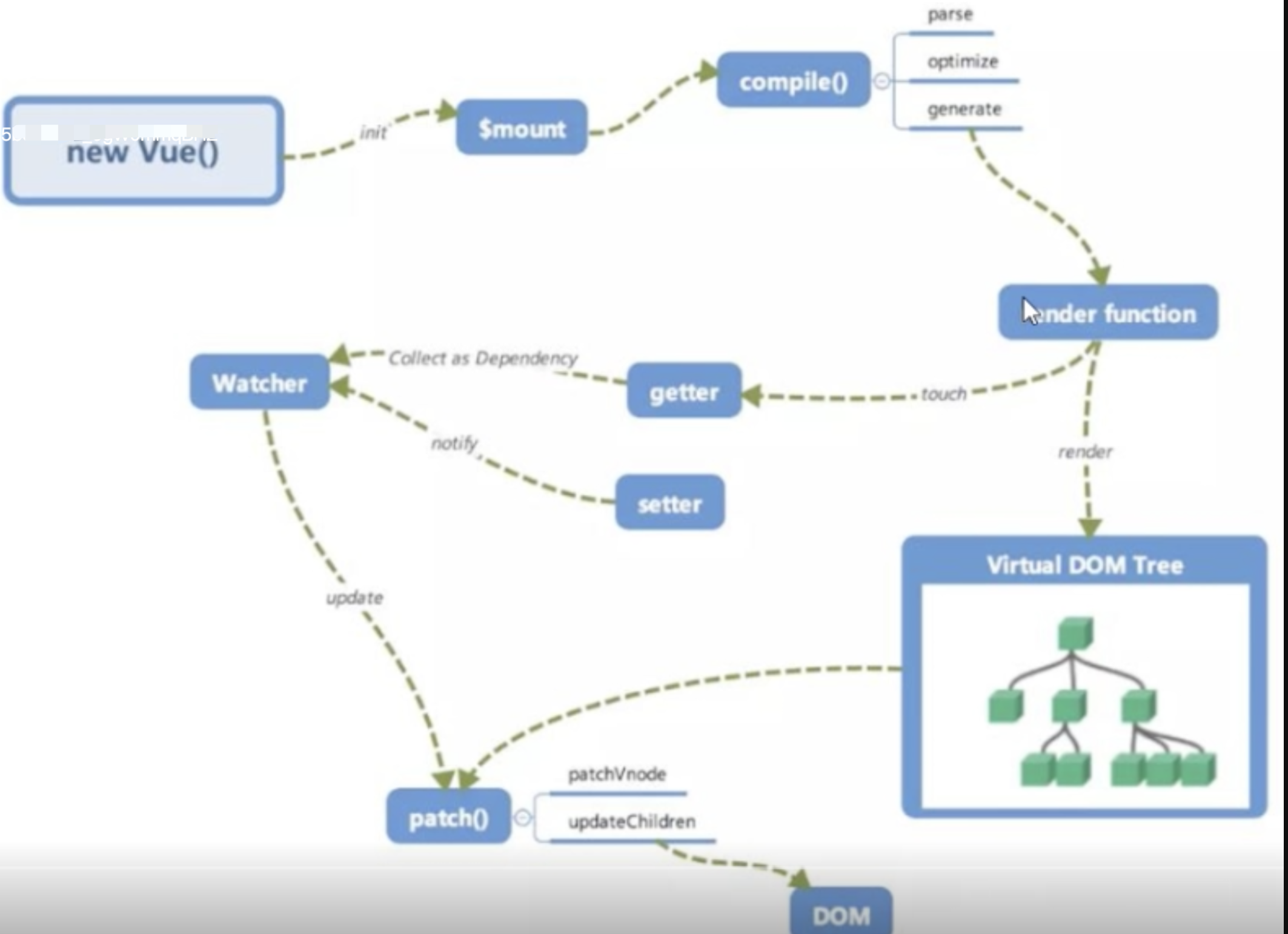
函数式组件优势和原理 函数组件的特点 函数式组件需要在声明组件是指定 functional:true不需要实例化,所以没有this,this通过render函数的第二个参数context来代替没有生命周期钩子函数,不能使用计算属性,watch不能通过$emit 对外暴露事件&…...

【Leetcode 剑指Offer】第 5 天 查找算法(中等)
查找算法剑指 Offer 04. 二维数组中的查找剑指 Offer 11. 旋转数组的最小数字剑指 Offer 50. 第一个只出现一次的字符Python字典基础哈希表(python中是dict())有序哈希表第一个中等,后两个简单题。剑指 Offer 04. 二维数组中的查找 题&#…...

薯条投放适合哪些笔记?小红书薯条投放的3种模式
随着小红书平台的种草推广模式兴盛,薯条投放这个词也渐渐进入大众的视野,今天就来给大家讲讲什么是薯条投放,以及薯条投放适合哪些笔记。一、什么是薯条投放?薯条是一款为小红书用户打造的笔记推广工具,用户可选择推广目标&#…...
记录第一个Python练习的过程
题目如下 编写一个名为collatz()的函数,它有一个名为number的参数。如果参数是偶数,那么collatz()就打印出number // 2,并返回该值。如果number是奇数,collatz()就打印并返回3 * number 1。 然后编写一个程序,让用户…...
【Python】3.3实现多线程
程序Program进程Process线程Thread为完成特定任务而用计算机语言编写的一组计算机能识别和执行的指令的集合。程序是指令、数据及其组织形式的描述,一段静态代码,静态对象。计算机中的程序关于某数据集合上的一次执行过程。进程是程序的实体,…...

在linux中使用lftp和sftp下载文件(夹)
一、首先确保你的系统中已经下载了lftp和sftp。 1.安装lftp sudo apt install lftp sudo apt install screen 2.安装sftp 在Linux系统中,一般RedHat系统默认已经安装了openssh-client和openssh-server,即默认已经集成了sftp服务,不需要重…...

Docker简介与用法
文章目录1、Docker简介1.1、Docker能解决什么问题1.2、什么是虚拟机技术1.2.1、虚拟机的缺点1.3、什么是容器1.3.1、容器与虚拟机比较1.4、分析 Docker 容器架构1.4.1、Docker客户端和服务器1.4.2、Docker 镜像(Image)1.4.3、Docker 容器(Container)1.4.4、Docker 仓库(reposit…...

基于海鸥算法改进的DELM分类-附代码
海鸥算法改进的深度极限学习机DELM的分类 文章目录海鸥算法改进的深度极限学习机DELM的分类1.ELM原理2.深度极限学习机(DELM)原理3.海鸥算法4.海鸥算法改进DELM5.实验结果6.参考文献7.Matlab代码1.ELM原理 ELM基础原理请参考:https://blog.c…...

linux基本功系列之mount命令实战
文章目录前言一. mount命令的介绍二. 语法格式及常用选项三. 参考案例3.1 将iso镜像挂载到/mnt上3.2 把某个分区挂载到/sdb1上3.3 用只读的形式把/dev/sdb2挂载到/sdb2上3.4 设置自动挂载总结前言 大家好,又见面了,我是沐风晓月,本文是专栏【…...
力扣Top100题之两数相加(Java解法)
0 题目描述 给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。 请你将两个数相加,并以相同形式返回一个表示和的链表。 你可以假设除了数字 0 之外,这两个数…...
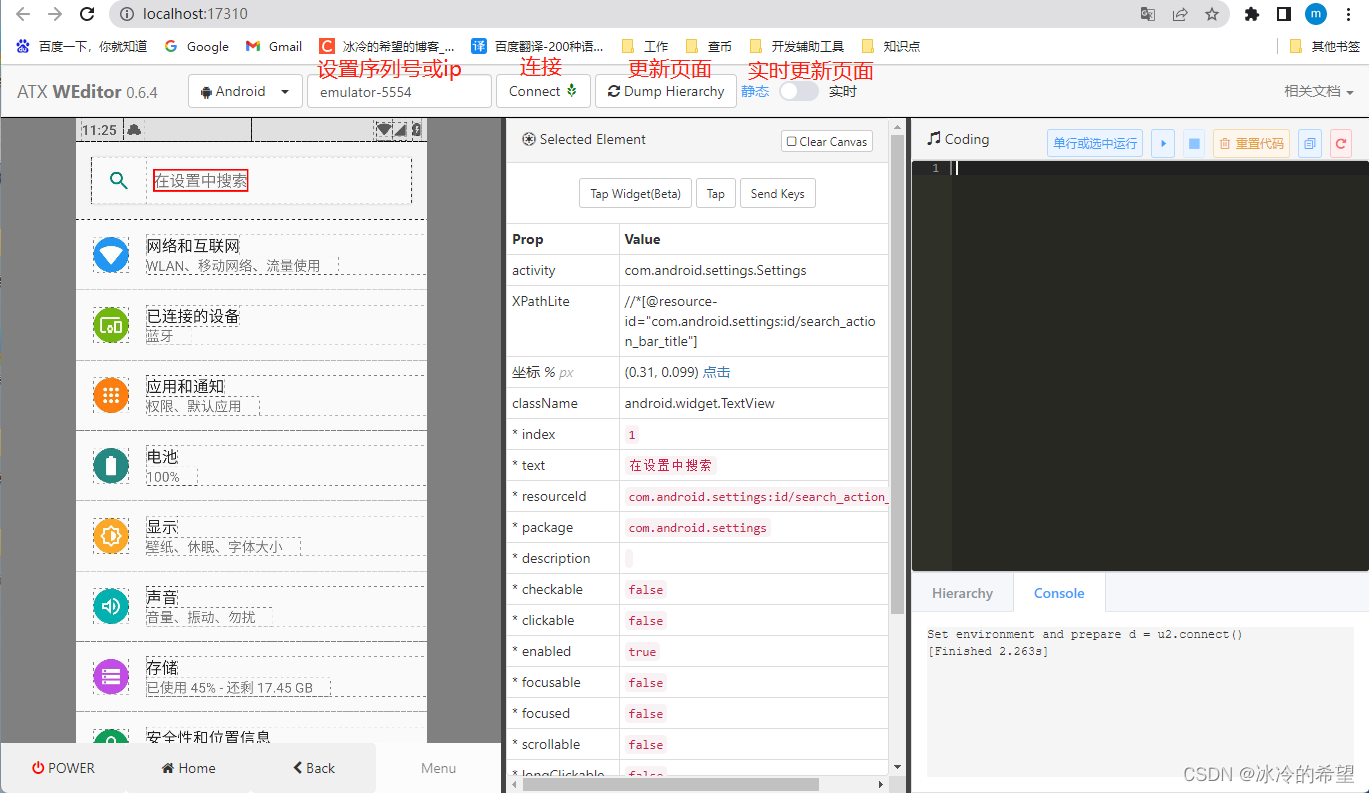
【测试】Python手机自动化测试库uiautomator2和weditor的详细使用
1.说明 我们之前在电脑操作手机进行自动化测试,基本上都是通过Appium的,这个工具确实强大,搭配谷歌官方的UiAutomator基本上可以完成各种测试,但缺点也很明显,配置环境太麻烦了,需要jdk、sdk等,…...

《NFL橄榄球》:旧金山49人·橄榄1号位
旧金山四九人(San Francisco 49ers,又译旧金山淘金者) 是美国全国橄榄球联盟球队。成立于1946年,最初作为全美橄榄球联合会(AAFC)的一员参加比赛,后于1950年与克利夫兰布朗一同加入由美国橄榄球联合会合并而成的NFL。现任主教练为…...
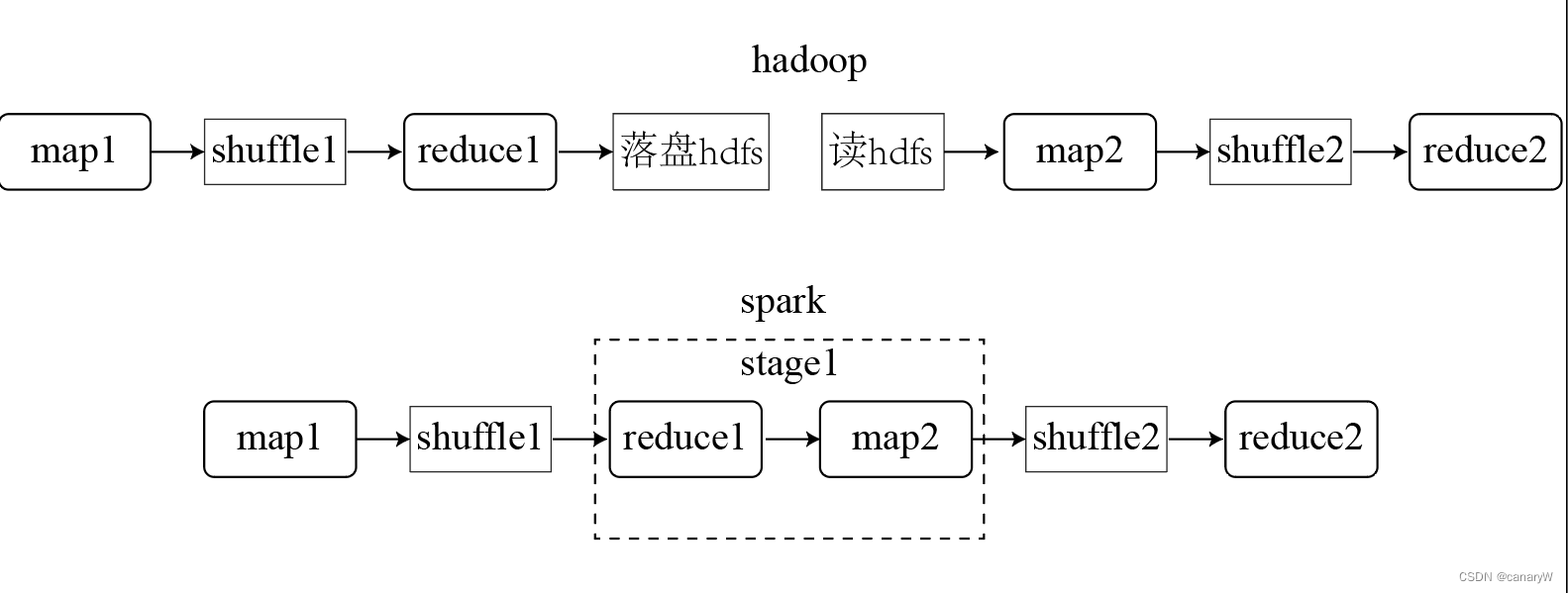
spark为什么比hadoop快
网上一堆人根本对计算框架一知半解就出来糊弄人,常见解答有: spark是基于内存计算,所以快。这跟废话似的,mr计算的时候不也是基于内存? mr shuffle落盘。这也是胡扯, spark shuffle不落盘? 实际…...

跨境人都在用的指纹浏览器到底有什么魔力?三分钟带你了解透彻
什么是指纹浏览器?这是东哥近期收到最多的粉丝私信咨询,指纹两个字大家都很熟悉,指纹浏览器就变得陌生起来。之前东哥也跟大家分享过很多次指纹浏览器的用法,鉴于还是很多人不认识这个好用的工具,东哥今天就来详细给大…...
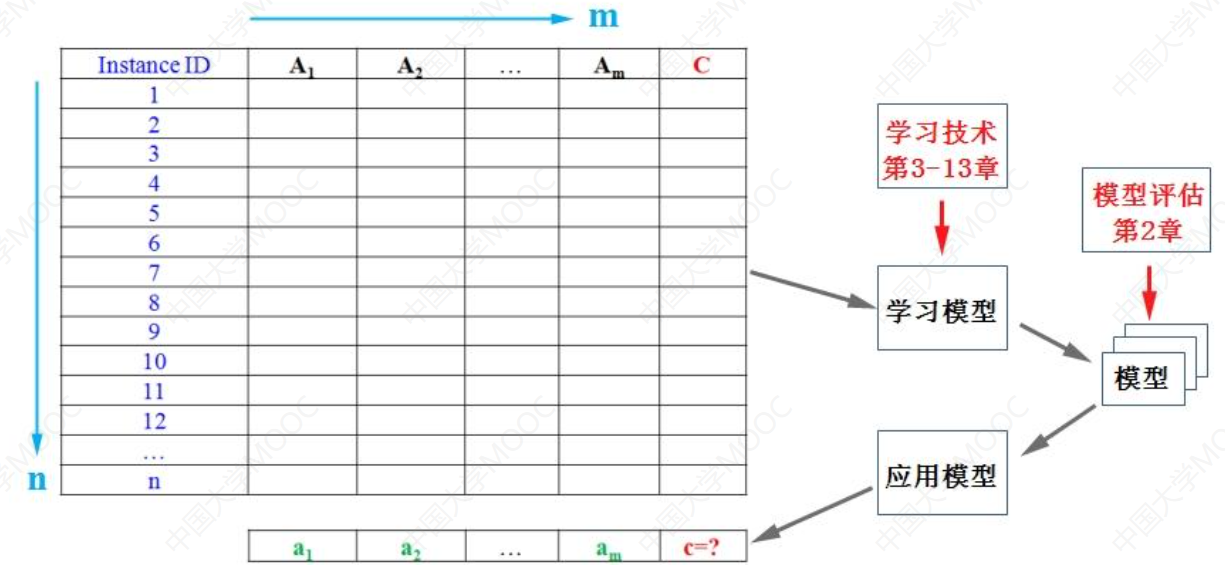
机器学习概述
机器学习是人工智能的核心研究领域之一,其研究动机是为了让计算机系统具有人的学习能力以便实现人工智能。目前被广泛采用的机器学习的定义是“利用经验来改善计算机系统自身的性能”。由于“经验在计算机系统中主要是以数据的形式存在的,因此机器学习需…...
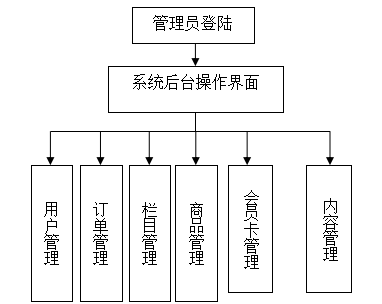
企业网站自动生成系统的设计和实现
技术:Java、JSP等摘要:随着Internet技术的发展,人们的日常生活已经离不开网络。未来社会人们的生活和工作将越来越依赖于数字技术的发展,越来越数字化、网络化、电子化、虚拟化。Internet的发展历程以及目前的应用状况和发展趋势&…...

sikuli+eclipse对于安卓app自动化测试的应用
Sikuli是什么? 下面是来自于官网的介绍:Sikuli is a visual technology to automate and test graphical user interfaces (GUI) using images (screenshots). Sikuli includes Sikuli Script, a visual scripting API for Jython, and Sikuli IDE, an …...
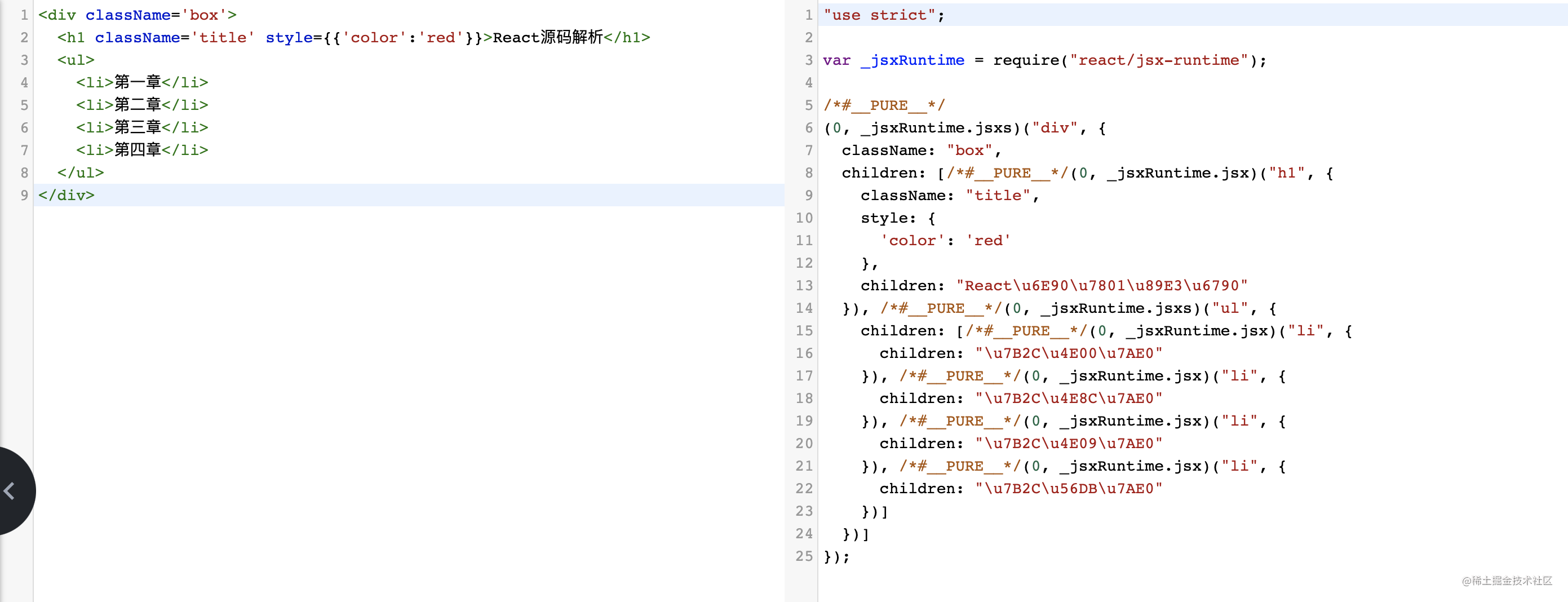
react源码分析:babel如何解析jsx
同作为MVVM框架,React相比于Vue来讲,上手更需要JavaScript功底深厚一些,本系列将阅读React相关源码,从jsx -> VDom -> RDOM等一些列的过程,将会在本系列中一一讲解 工欲善其事,必先利其器 经过多年的…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
