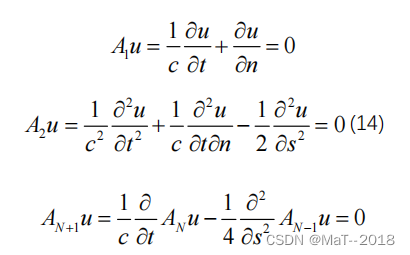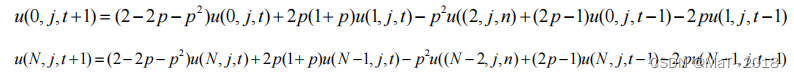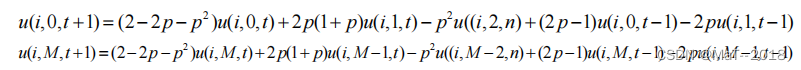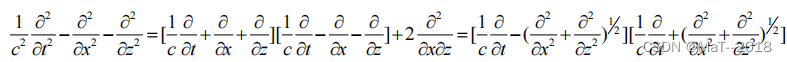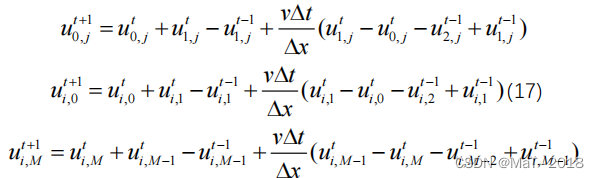正演(1): 二维声波正演模拟程序(中心差分)Python实现
目录
1、原理:
1)二维声波波动方程:
编辑
2)收敛条件(不是很明白)
3)雷克子波
4)二维空间衰减函数
5)边界吸收条件 (不是很明白。。)
2、编程实现
1)参数设置:
2)雷克子波及二维空间衰减函数
3)边界吸收条件
4)波动方程,迭代公式:
5)全部代码如下:
3、基于matlab的二维波动方程实现
波动方程数值解是波动方程正演、逆时偏移和全波形反演的核心技术之一。本文采用二阶有限差分对波动方程进行了离散,进而实现了对波动方程的数值求解,模拟出其在介质中的传播过程。
NumPy 通常与 SciPy(Scientific Python)和 Matplotlib(绘图库)一起使用, 这种组合广泛用于替代 MatLab,是一个强大的科学计算环境,有助于我们通过 Python 学习数据科学或者机器学习。
SciPy 包含的模块有最优化、线性代数、积分、插值、特殊函数、快速傅里叶变换、信号处理和图像处理、常微分方程求解和其他科学与工程中常用的计算。
Matplotlib 是 Python 编程语言及其数值数学扩展包 NumPy 的可视化操作界面。它为利用通用的图形用户界面工具包,如 Tkinter, wxPython, Qt 或 GTK+ 向应用程序嵌入式绘图提供了应用程序接口(API)。
本文代码部分才用了 NumPy和Matplotlib包。
1、原理:
1)二维声波波动方程:

其中u 为声压,f 为震源中心声压,x/z 为x/z 方向的采样点,t 为时间,v 为速度。
利用泰勒公式对进行展开得到:
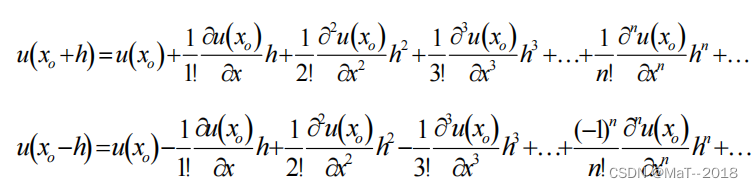
两式相减得:
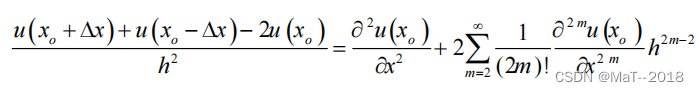
则有:
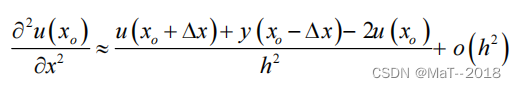
近似得二阶差分算子:
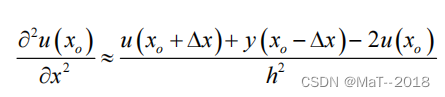
利用二阶中心差分算子对二阶导数进行离散:
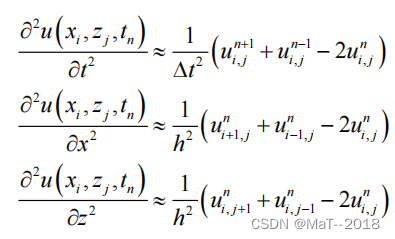
将上式代入声波方程得到二阶中心差分格式:
![]()
其空间和时间差分格式示意图如下图所示:
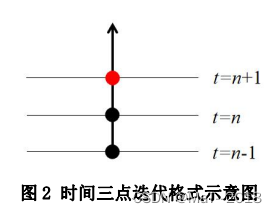
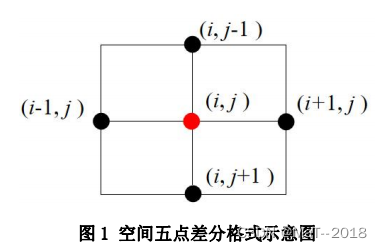
2)收敛条件(不是很明白)
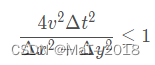
3)雷克子波
雷克子波是地震子波中的一种。由震源激发、经地下传播并被人们在地面或井中接收到的地震波通常是一个短的脉冲振动,称该振动为振动子波, 如下图所示。
公式为: f(t)=(1-2*(pi*f*t)^2)*exp(-(pi*f*t)^2) ,其中t 为时间,f 为主频。
4)二维空间衰减函数
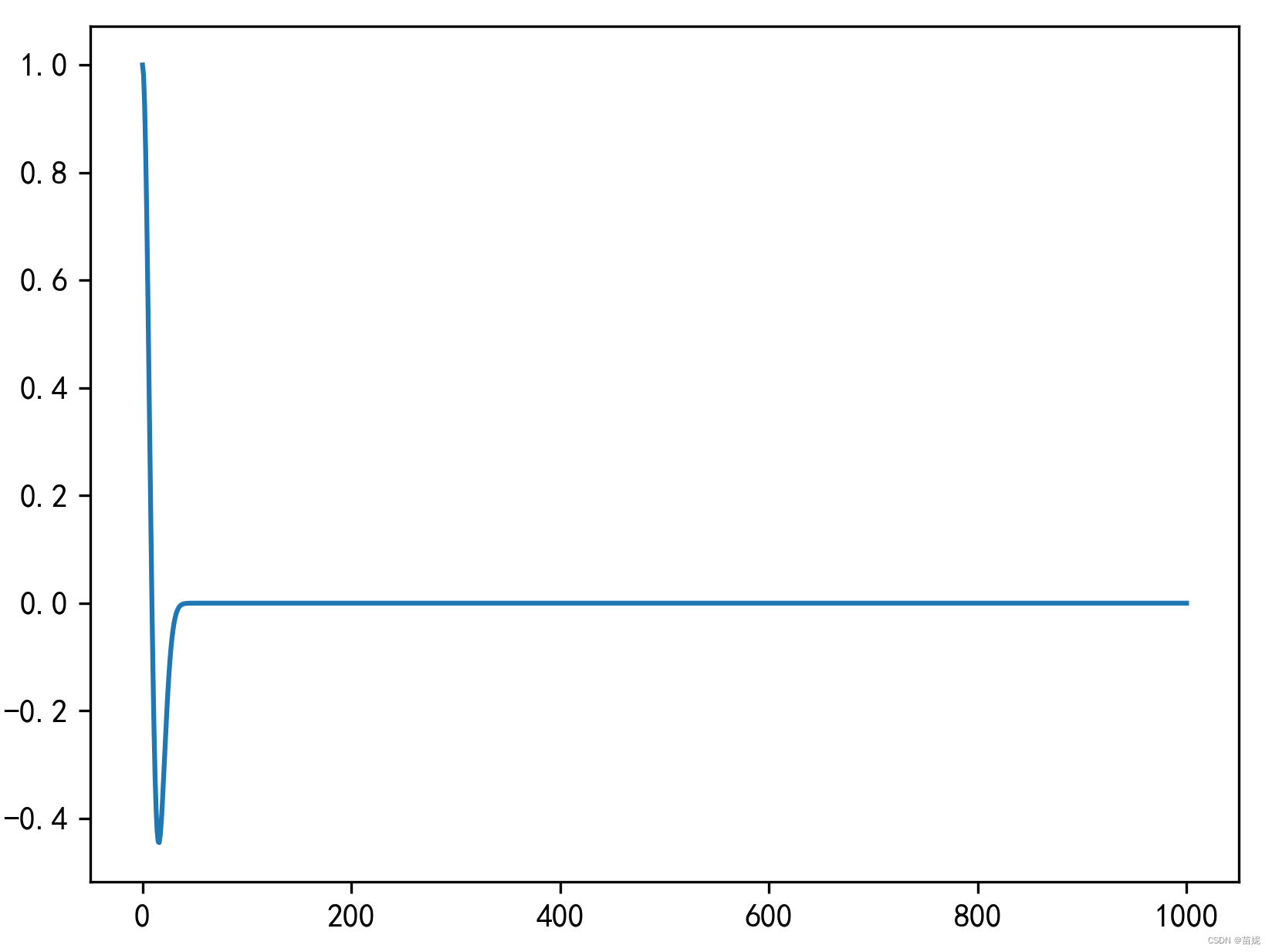
震源中心为1,不衰减,距离中心越远,衰减程度越大。
h_x_z = np.zeros((Nx+1,Nz+1)) #np.exp(-0.25 * ((x - Nx//2)**2 + (z - Nz//2)**2)) 二维空间衰减函数
h_x_z[Nx//2,Nz//2] = 1 # 在Nx//2,Nz//2处激发
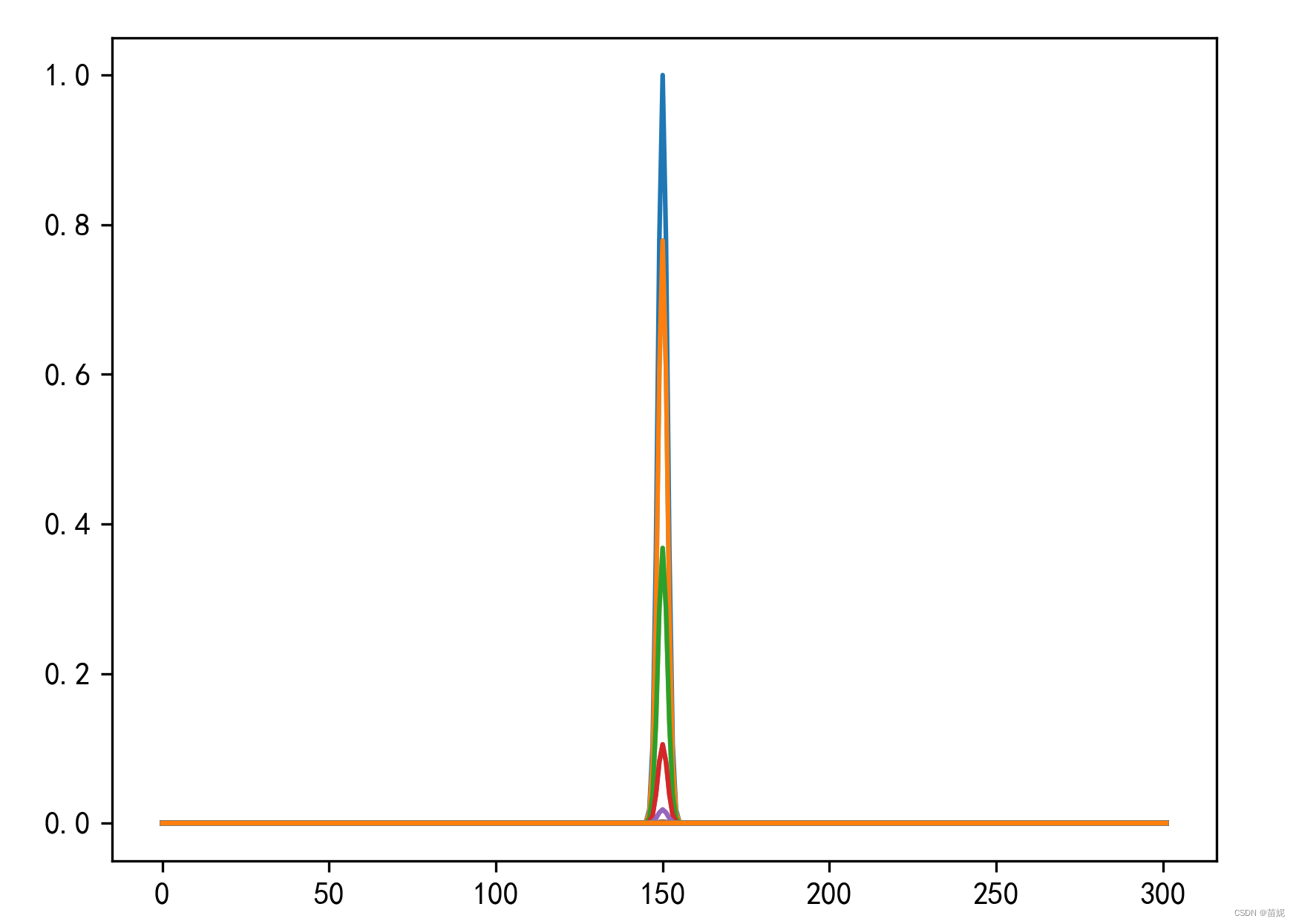
h_x_z = np.exp(-alpha ** 2 * ((x - Nx//2)**2 + (z - Nz//2)**2)) # 二维空间衰减函数下图显示的是h_x_z[150] 的曲线,整个的二维空间衰减系数h_x_z,以[150,150] 为中心(震源),向四周衰减。
5)边界吸收条件 (不是很明白。。)
作用:声波传播时是没有边界的,因此也不存在边界反射问题。但由于模拟正演时,观测范围有限,因此必然是有边界的,边界吸收条件就是尽可能的将能量吸收,将边界反射降到最低。(我的理解哈,欢迎讨论)以下是两种边界吸收条件。
Clayton-Engquist 单成波吸收边界条件: 最早是由 Clayton 等人发现并推广的, 其微分表达式为:
其中:n 为边界的外法线方向; s 边界的切线方向。
对上式进行离散得到上、下、左、右边界差分格式如下:
其中:N 、 M 为边界的网格数。
Reynolds 边界条件:对于二维声波波动方程,应用二维声波方的微分算子可以,得到:
对上式进行离散可得上下左右边界计算公式:
2、编程实现
1)参数设置:
- x/z方向长度1500m,x/z方向空间步长5m,每个方向的采样点数为301;
- 模拟时长1s,时间步长0.001s,时间采样数1000;
- 震源频率25Hz;
- 空间衰减因子0.5;
- 波速固定,任何位置都为3000m/s
- 震源位置在中心;初始声压为0。
# 区域大小
Nx = 301
Nz = 301
# 空间间隔
dx = h
dy = h# 时间采样数
Nt = 1000
# 时间步
dt = 1 / Nt# 速度模型
v = np.ones((Nx+1,Nz+1)) * 3000
u = np.zeros((Nt+1,Nx+1,Nz+1))
h = 5# 子波主频
fm = 25
# 空间衰减因子
alpha = 0.5# 迭代公式中的r
A = v **2 * dt ** 2 / h ** 2
C = v * dt / h
2)雷克子波及二维空间衰减函数
t = np.arange(0, Nt+1)
t0 = 0 # 延迟时间,相当于在t=t0时激发 ,震幅在t0时最大,相位也在此
s_t = (1 - 2 * (np.pi * fm * dt * (t - t0)) ** 2) * np.exp( - (np.pi * fm * dt * (t - t0)) ** 2)x = np.arange(0,Nx+1)
z = np.arange(0,Nz+1)
x,z = np.meshgrid(x,z)h_x_z = np.zeros((Nx+1,Nz+1)) #np.exp(-0.25 * ((x - Nx//2)**2 + (z - Nz//2)**2)) 二维空间衰减函数
h_x_z[Nx//2,Nz//2] = 1 # 在Nx//2,Nz//2处激发
h_x_z = np.exp(-alpha ** 2 * ((x - Nx//2)**2 + (z - Nz//2)**2)) # 二维空间衰减函数x0 = Nx // 2
z0 = Nz // 2
u0 = lambda r, s: 0.25*np.exp(-((r-x0)**2+(s-z0)**2))
JJ = np.arange(1,Nz)
II = np.arange(1,Nx)
II,JJ = np.meshgrid(II,JJ)
3)边界吸收条件
# 边界条件
ii = np.arange(Nx+1)
jj = np.arange(Nz+1)
# Clayton-Engquist-majda 二阶吸收边界条件
u[t+1, 0, jj] = (2 - 2 * C[ 0, jj] - C[ 0, jj] ** 2) * u[t, 0, jj] \+ 2 * C[ 1, jj] * (1 + C[ 1, jj]) * u[t, 1, jj] \- C[ 2, jj] ** 2 * u[t, 2, jj] \+ (2 * C[ 0, jj] - 1) * u[t - 1, 0, jj] \- 2 * C[ 1, jj] * u[t - 1, 1, jj]# 下部
u[t+1, -1, jj] = (2 - 2 * C[ -1, jj] - C[ -1, jj] ** 2) * u[t, -1, jj] \+ 2 * C[ -2, jj] * (1 + C[ -2, jj]) * u[t, -2, jj] \- C[ -3, jj] ** 2 * u[t, -3, jj] \+ (2 * C[ -1, jj] - 1) * u[t - 1, -1, jj] \- 2 * C[ -2, jj] * u[t - 1, -2, jj]# 左部
u[t+1, ii, 0] = (2 - 2 * C[ii, 0] - C[ii, 0] ** 2) * u[t, ii, 0] \+ 2 * C[ii, 1] * (1 + C[ii, 1]) * u[t, ii, 1] \- C[ii, 2] ** 2 * u[t, ii, 2] \+ (2 * C[ii, 0] - 1) * u[t - 1, ii, 0] \- 2 * C[ii, 1] * u[t - 1, ii, 1]
# 右部
u[t+1, ii, -1] = (2 - 2 * C[ii, -1] - C[ii, -1] ** 2) * u[t, ii, -1] \+ 2 * C[ii, -2] * (1 + C[ii, -2]) * u[t, ii, -2] \- C[ii, -3] ** 2 * u[t, ii, -3] \+ (2 * C[ii, -1] - 1) * u[t - 1, ii, -1] \- 2 * C[ii, -2] * u[t - 1, ii, -2]
#Reynolds 边界条件
u[t+1,ii, 0] = u[t,ii, 0] + u[t,ii, 1] - u[t-1,ii, 1] + C[ii, 1]*u[t,ii, 1] - C[ii, 0]*u[t,ii, 0] -C[ii, 2]*u[t-1,ii, 2] +C[ii, 1]*u[t-1,ii, 1]u[t+1,ii,-1] = u[t,ii,-1] + u[t,ii,-2] - u[t-1,ii,-2] + C[ii,-2]*u[t,ii,-2] - C[ii,-1]*u[t,ii,-1] -C[ii,-3]*u[t-1,ii,-3] +C[ii,-2]*u[t-1,ii,-2]u[t+1, 0,jj] = u[t, 0,jj] + u[t, 1,jj] - u[t-1, 1,jj] + C[ 1,jj]*u[t, 1,jj] - C[ 0,jj]*u[t, 0,jj] -C[ 2,jj]*u[t-1, 2,jj] +C[ 1,jj]*u[t-1, 1,jj]u[t+1,-1,jj] = u[t,-1,jj] + u[t,-2,jj] - u[t-1,-2,jj] + C[-2,jj]*u[t,-2,jj] - C[-1,jj]*u[t,-1,jj] -C[-3,jj]*u[t-1,-3,jj] +C[-1,jj]*u[t-1,-2,jj]
4)波动方程,迭代公式:
# 迭代公式
u[t+1,II,JJ] = s_t[t]*h_x_z[II,JJ]+A[II,JJ]*(u[t,II,JJ+1]+u[t,II,JJ-1]+u[t,II+1,JJ]+u[t,II-1,JJ])+(2-4*A[II,JJ])*u[t,II,JJ]-u[t-1,II,JJ]
5)全部代码如下:
import numpy as np
import imageio.v2 as imageio
import os
import pandas as pd
from matplotlib import pyplot as plt
# 解决中文问题
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = FalseNx = 301
Nz = 301
Nt = 1000
v = np.ones((Nx+1,Nz+1)) * 3000
h = 5
fm = 25
alpha = 0.5
dt = 1 / Nt
dx = h
dy = h
A = v **2 * dt ** 2 / h ** 2
C = v * dt / hr = np.max(v)*dt/h
assert r < 0.707,f'r should < 0.707, but is {r}'
u = np.zeros((Nt+1,Nx+1,Nz+1))t = np.arange(0, Nt+1)
t0 = 0 # 延迟时间,相当于在t=t0时激发 ,震幅在t0时最大,相位也在此
s_t = (1 - 2 * (np.pi * fm * dt * (t - t0)) ** 2) * np.exp( - (np.pi * fm * dt * (t - t0)) ** 2)plt.plot(s_t)
plt.show()x = np.arange(0,Nx+1)
z = np.arange(0,Nz+1)
x,z = np.meshgrid(x,z)
# print(((z - Nz//2)**2).shape)h_x_z = np.zeros((Nx+1,Nz+1)) #np.exp(-0.25 * ((x - Nx//2)**2 + (z - Nz//2)**2)) 二维空间衰减函数
h_x_z[Nx//2,Nz//2] = 1 # 在Nx//2,Nz//2处激发
h_x_z = np.exp(-alpha ** 2 * ((x - Nx//2)**2 + (z - Nz//2)**2)) # 二维空间衰减函数JJ = np.arange(1,Nz)
II = np.arange(1,Nx)
II,JJ = np.meshgrid(II,JJ)mode = 'c_e'
img_path = './2_order'
if not os.path.exists(img_path):os.makedirs(img_path)for t in range(2,Nt):print('\rstep {} / {}'.format(t ,Nt), end="")# 边界条件ii = np.arange(Nx+1)jj = np.arange(Nz+1)if mode == 'c_e':# Clayton-Engquist-majda 二阶吸收边界条件u[t+1, 0, jj] = (2 - 2 * C[ 0, jj] - C[ 0, jj] ** 2) * u[t, 0, jj] \+ 2 * C[ 1, jj] * (1 + C[ 1, jj]) * u[t, 1, jj] \- C[ 2, jj] ** 2 * u[t, 2, jj] \+ (2 * C[ 0, jj] - 1) * u[t - 1, 0, jj] \- 2 * C[ 1, jj] * u[t - 1, 1, jj]# 下部u[t+1, -1, jj] = (2 - 2 * C[ -1, jj] - C[ -1, jj] ** 2) * u[t, -1, jj] \+ 2 * C[ -2, jj] * (1 + C[ -2, jj]) * u[t, -2, jj] \- C[ -3, jj] ** 2 * u[t, -3, jj] \+ (2 * C[ -1, jj] - 1) * u[t - 1, -1, jj] \- 2 * C[ -2, jj] * u[t - 1, -2, jj]# 左部u[t+1, ii, 0] = (2 - 2 * C[ii, 0] - C[ii, 0] ** 2) * u[t, ii, 0] \+ 2 * C[ii, 1] * (1 + C[ii, 1]) * u[t, ii, 1] \- C[ii, 2] ** 2 * u[t, ii, 2] \+ (2 * C[ii, 0] - 1) * u[t - 1, ii, 0] \- 2 * C[ii, 1] * u[t - 1, ii, 1]# 右部u[t+1, ii, -1] = (2 - 2 * C[ii, -1] - C[ii, -1] ** 2) * u[t, ii, -1] \+ 2 * C[ii, -2] * (1 + C[ii, -2]) * u[t, ii, -2] \- C[ii, -3] ** 2 * u[t, ii, -3] \+ (2 * C[ii, -1] - 1) * u[t - 1, ii, -1] \- 2 * C[ii, -2] * u[t - 1, ii, -2]if mode == 're':#Reynolds 边界条件u[t+1,ii, 0] = u[t,ii, 0] + u[t,ii, 1] - u[t-1,ii, 1] + C[ii, 1]*u[t,ii, 1] - C[ii, 0]*u[t,ii, 0] -C[ii, 2]*u[t-1,ii, 2] +C[ii, 1]*u[t-1,ii, 1]u[t+1,ii,-1] = u[t,ii,-1] + u[t,ii,-2] - u[t-1,ii,-2] + C[ii,-2]*u[t,ii,-2] - C[ii,-1]*u[t,ii,-1] -C[ii,-3]*u[t-1,ii,-3] +C[ii,-2]*u[t-1,ii,-2]u[t+1, 0,jj] = u[t, 0,jj] + u[t, 1,jj] - u[t-1, 1,jj] + C[ 1,jj]*u[t, 1,jj] - C[ 0,jj]*u[t, 0,jj] -C[ 2,jj]*u[t-1, 2,jj] +C[ 1,jj]*u[t-1, 1,jj]u[t+1,-1,jj] = u[t,-1,jj] + u[t,-2,jj] - u[t-1,-2,jj] + C[-2,jj]*u[t,-2,jj] - C[-1,jj]*u[t,-1,jj] -C[-3,jj]*u[t-1,-3,jj] +C[-1,jj]*u[t-1,-2,jj]# 迭代公式u[t+1,II,JJ] = s_t[t]*h_x_z[II,JJ]*v[II, JJ]**2*dt**2+A[II,JJ]*(u[t,II,JJ+1]+u[t,II,JJ-1]+u[t,II+1,JJ]+u[t,II-1,JJ])+(2-4*A[II,JJ])*u[t,II,JJ]-u[t-1,II,JJ]plt.imshow(u[t], cmap='gray_r') # 'seismic' gray_r# plt.axis('off') # 隐藏坐标轴plt.colorbar()if t % 10 == 0:plt.savefig(os.path.join(img_path, str(t) + '.png'),bbox_inches="tight", # 去除坐标轴占用空间pad_inches=0.0) # 去除所有白边plt.pause(0.05)plt.cla()plt.clf() # 清除所有轴,但是窗口打开,这样它可以被重复使用
plt.close()# 保存gif
filenames=[]
for files in os.listdir(img_path ):if files.endswith('jpg') or files.endswith('jpeg') or files.endswith('png'):file=os.path.join(img_path ,files)filenames.append(file)images = []
for filename in filenames:images.append(imageio.imread(filename))imageio.mimsave(os.path.join(img_path, 'wave.gif'), images,duration=0.0001)
参考:
波动方程数值求解(一)_声波方程的解_MaT--2018的博客-CSDN博客
3、基于matlab的二维波动方程实现
close all
clear
clc% 此程序是有限差分法实现声波方程数值模拟%% 参数设置
delta_t = 0.001; % s
delta_s = 10; % 空间差分:delta_s = delta_x = delta_y (m)
nx = 800;
ny = 800;
nt = 1000;
fmain = 12.5;
%loop:按照10000s为一次大循环;slice代表每隔1000s做一个切片
loop_num = 3;
slice = 1000;
slice_index = 1;
%% 初始化
%震源
t = 1:nt;
t0 = 50;
s_t = (1-2*(pi*fmain*delta_t*(t-t0)).^2).*exp(-(pi*fmain*delta_t*(t-t0)).^2);%源
%一个loop代表向后计算10000s,目的是减少内存消耗
%间隔1000s保存一张切片
num_slice = nt*loop_num/slice;
U_loop(1:ny,1:nx,1:num_slice) = 0;
U_next_loop(1:ny,1:nx,1:2) = 0;
%初始化数组变量
w(1:ny,1:nx) = 0;
U(1:ny,1:nx,1:nt) = 0;
w(400,400) = 1;
V(1:ny,1:nx) = 2000;
A = V.^2*delta_t^2/delta_s^2;
B = V*delta_t/delta_s;%% 开始计算
JJ = 2:ny-1;
II = 2:nx-1;
start_time = clock;
for loop = 1:loop_numfprintf('Loop=%d\n',loop)for i_t = 2:nt-1if(loop>1)s_t(i_t) = 0;end%上边界U(1,II,i_t+1) = (2-2*B(1,II)-A(1,II)).*U(1,II,i_t)+2*B(1,II).*(1+B(1,II)).*U(2,II,i_t)...-A(1,II).*U(3,II,i_t)+(2*B(1,II)-1).*U(1,II,i_t-1)-2*B(1,II).*U(2,II,i_t-1);%下边界U(ny,II,i_t+1) = (2-2*B(ny,II)-A(ny,II)).*U(ny,II,i_t)+2*B(ny,II).*(1+B(ny,II)).*U(ny-1,II,i_t)...-A(ny,II).*U(ny-2,II,i_t)+(2*B(ny,II)-1).*U(ny,II,i_t-1)-2*B(1,II).*U(ny-1,II,i_t-1);%左边界U(JJ,1,i_t+1) = (2-2*B(JJ,1)-A(JJ,1)).*U(JJ,1,i_t)+2*B(JJ,1).*(1+B(JJ,1)).*U(JJ,1+1,i_t)...-A(JJ,1).*U(JJ,1+2,i_t)+(2*B(JJ,1)-1).*U(JJ,1,i_t-1)-2*B(JJ,1).*U(JJ,1+1,i_t-1);%右边界U(JJ,nx,i_t+1) = (2-2*B(JJ,nx)-A(JJ,nx)).*U(JJ,nx,i_t)+2*B(JJ,nx).*(1+B(JJ,nx)).*U(JJ,nx-1,i_t)...-A(JJ,nx).*U(JJ,nx-2,i_t)+(2*B(JJ,nx)-1).*U(JJ,nx,i_t-1)-2*B(JJ,nx).*U(JJ,nx-1,i_t-1);%递推公式U(JJ,II,i_t+1) = s_t(i_t).*w(JJ,II)+A(JJ,II).*(U(JJ,II+1,i_t)+U(JJ,II-1,i_t)+U(JJ+1,II,i_t)+U(JJ-1,II,i_t))+...(2-4*A(JJ,II)).*U(JJ,II,i_t)-U(JJ,II,i_t-1);if(mod(i_t,100)==0)run_time = etime(clock,start_time);fprintf('step=%d,total=%d,累计耗时%.2fs\n',i_t+(loop-1)*nt,nt*loop_num,run_time)U_loop(:,:,slice_index) = U(:,:,i_t);slice_index = slice_index +1;endend%处理四个角点KK = 1:nt;U(1,1,KK) = 1/2*(U(1,2,KK)+U(2,1,KK));U(1,nx,KK) = 1/2*(U(1,nx-1,KK)+U(2,nx,KK));U(ny,1,KK) = 1/2*(U(ny-1,1,KK)+U(ny,2,KK));U(ny,nx,KK) = 1/2*(U(ny-1,nx,KK)+U(ny,nx-1,KK));%% 为下一次loop做准备fprintf('step=%d,total=%d,累计耗时%.2fs\n',i_t+1+(loop-1)*nt,nt*loop_num,run_time)U_loop(:,:,slice_index) = U(:,:,nt);slice_index = slice_index +1;U_next_loop(:,:,1)=U(:,:,nt-1);U_next_loop(:,:,2)=U(:,:,nt);U(:,:,:) = 0;U(:,:,1) = U_next_loop(:,:,1);U(:,:,2) = U_next_loop(:,:,2);
end%% 制作动图
fmat=moviein(num_slice);
filename = 'FDM_4_homogenerous.gif';
for II = 1:num_slicepcolor(U_loop(:,:,II));shading interp;axis tight;set(gca,'yDir','reverse');str_title = ['FDM-4-homogenerous t=',num2str(delta_t*II*100),'s'];title(str_title)drawnow; %刷新屏幕F = getframe(gcf);%捕获图窗作为影片帧I = frame2im(F); %返回图像数据[I, map] = rgb2ind(I, 256); %将rgb转换成索引图像if II == 1imwrite(I,map, filename,'gif', 'Loopcount',inf,'DelayTime',0.1);elseimwrite(I,map, filename,'gif','WriteMode','append','DelayTime',0.1);endfmat(:,II)=getframe;
end
movie(fmat,10,5);
%% 绘图为gif
pcolor(U_loop(:,:,num_slice))
shading interp;
axis tight;
set(gca,'yDir','reverse');
str_title = ['FDM-4-homogenerous t=',num2str(delta_t*num_slice*100),'s'];
title(str_title)
colormap('Gray')
filename = [str_title,'.jpg'];
saveas(gcf,filename)%% 耗时
toc
相关文章:
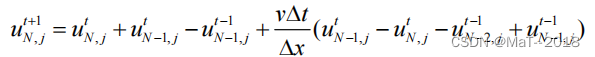
正演(1): 二维声波正演模拟程序(中心差分)Python实现
目录 1、原理: 1)二维声波波动方程: 编辑 2)收敛条件(不是很明白) 3)雷克子波 4)二维空间衰减函数 5)边界吸收条件 (不是很明白。。) 2、编程实现 1)参数设置&…...

珠海数据智能监控器+SaaS平台 轻松实现SMT生产管控
数据智能监控器 兼容市面上99%的SMT设备 直接读取设备生产数据与状态,如:计划产出、实际产出、累计产出、停机、节拍、线利用率、直通率、停产时间、工单状态、OEE…… 产品功能价值 ◎ OEE不达标报警,一手掌握生产效能 ◎ 首检/巡检/成…...

习题22对前面21节的归纳总结
笨方法学python --习题22 Vi---Rum 于 2021-01-12 14:16:10 发布 python 习题22 这节内容主要是归纳总结 ex1.py 第一次学习 1.print:打印 2.# :是注释的意思,井号右边的内容不再执行 3.end"":,在句子结尾加上这个就不会再换行…...

使用Vite快速构建前端React项目
一、Vite简介 Vite是一种面向现代浏览器的一个更轻、更快的前端构建工具,能够显著提升前端开发体验。除了Vite外,前端著名的构建工具还有Webpack和Gulp。目前,Vite已经发布了Vite3,Vite全新的插件架构、丝滑的开发体验,可以和Vue3完美结合。 相比Webpack和Gulp等构建工具…...

人工智能高等数学--人工智能需要的数学知识_微积分_线性代数_概率论_最优化---人工智能工作笔记0024
然后我们看一下人工智能中需要的数学知识 数学知识是重要的,对于理解人工智能底层原理来说很重要,但是工作中 工作中一般都不会涉及的自己写算法之类的,只是面试,或者理解底层原理的时候需要 然后看一下人工智能需要哪些数学知识 这里需要微积分 线性代数 概率论 最优化的知识…...
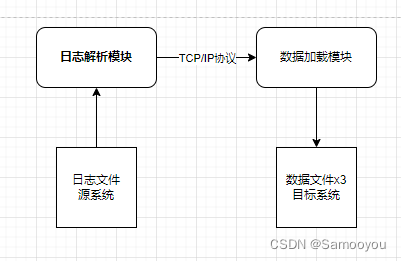
阿里大数据之路总结
一、数据采集 二、数据同步 2.1、数据同步方式: 数据同步的三种方式:直连方式、数据文件同步、数据库日志解析方式 关系型数据库的结构化数据:MYSQL、Oracle、DB2、SQL Server非关系型数据库的非结构化数据(数据库表形式存储&am…...
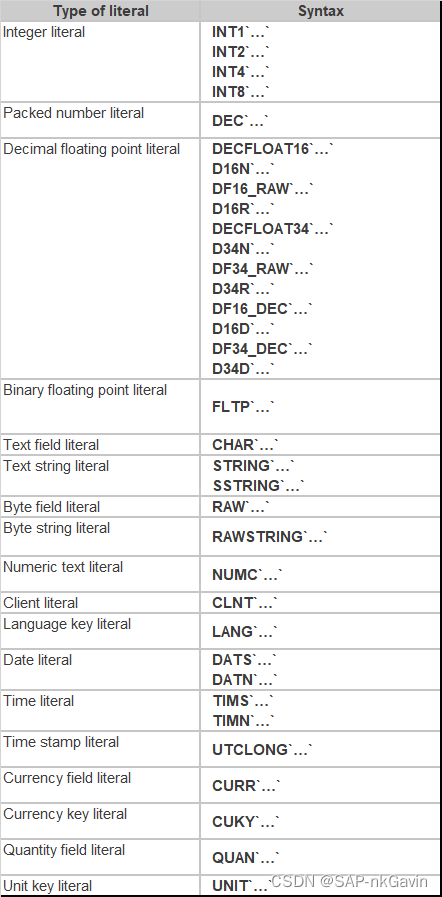
ABAP中Literals的用法(untyped literal vs. typed literal)
1. 什么是Literals ? Literals的字面意思即“文字”。其实,Literals就是在ABAP代码中直接指定的一个字符串,但注意哦,这个字符串并不意味着其类型一定是string哦。 要弄清这个概念,就要清楚ABAP对于Literals 的定义和处理方式。…...

tensorflow1.14.0安装教程
1首先电脑安装好Anaconda3(Anaconda介绍、安装及使用教程 - 知乎 (zhihu.com),) 蟒蛇 |全球最受欢迎的数据科学平台 (anaconda.com) 2打开Anaconda Prompt(本人更新win11后,主菜单不再显示,那么我们可以打…...

C++赋值运算符重载
赋值运算符重载 目录赋值运算符重载示例1:示例2:示例3:示例4:很巧妙的是,在编写这篇文章时(2023年2月27日),再加100天就是6月7日,恰好是今年高考的百日誓师! …...
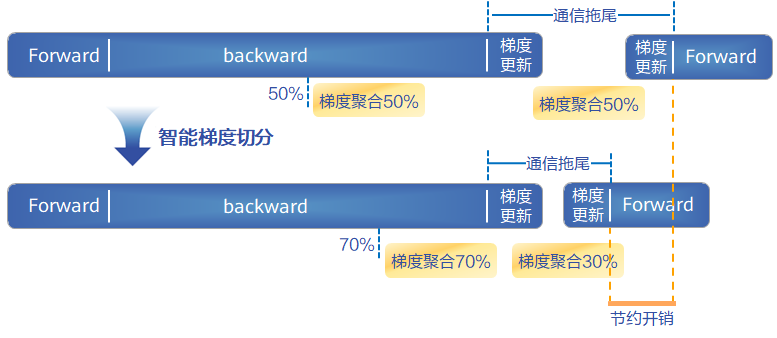
网络性能总不好?专家帮你来“看看”— CANN 6.0 黑科技 | 网络调优专家AOE,性能效率双提升
随着深度学习模型复杂度和数据集规模的增大,计算效率的提升成为不可忽视的问题。然而,算法网络的多样性、输入数据的不确定性以及硬件之间的差异性,使得网络调优耗费巨大成本,即使是经验丰富的专家,也需要耗费数天的时…...
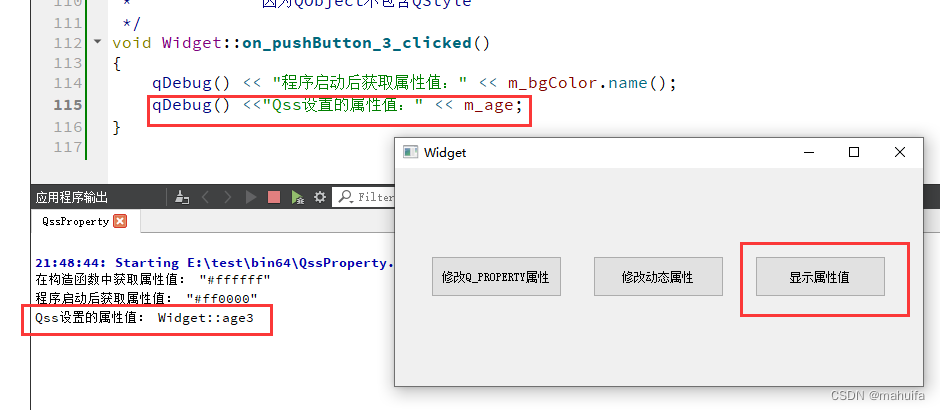
Qss自定义属性
QSS自定义属性 更多精彩内容👉个人内容分类汇总 👈👉QSS样式学习 👈文章目录QSS自定义属性[toc]前言一、实现效果二、使用方式1.QSS设置Q_PROPERTY属性样式2.QSS设置动态属性样式3.qproperty-<属性名称>语法14.qproperty-&…...
连接金蝶云星空,数据交互轻松搞定!丨三叠云
金蝶云星空 路径 拓展 >> 插件 功能简介 新增插件「金蝶云星空」。 用户可通过配置「金蝶云星空」插件,就可以实时获取「金蝶云星空」的数据,同时支持回填数据至金蝶系统内。 地图视图 路径 表单 >> 表单设计 功能简介 新增「地图视…...

JSX是什么,React为什么使用JSX,babel怎么转译JSX的
JSX是什么,React为什么使用JSX,babel怎么转译JSX的 在前端的框架中有两种“描述UI”的方案,一种是JSX语法,一种是模板语言。 其中React就是选择的JSX,Vue就是选择的模板语言。 JSX其实就是一个语法糖,在…...

从工地转行软件测试,拿下13k+年终奖是种什么体验?
最近,一则名为《我:毕业五年,存款5000。她:中传硕士,火锅店保洁》的视频走红网络,两位名校毕业生看似高开低走的就业经历,引起了很多人的共鸣。她们所传达的并不是所谓的躺平、摆烂,而是希望更多…...
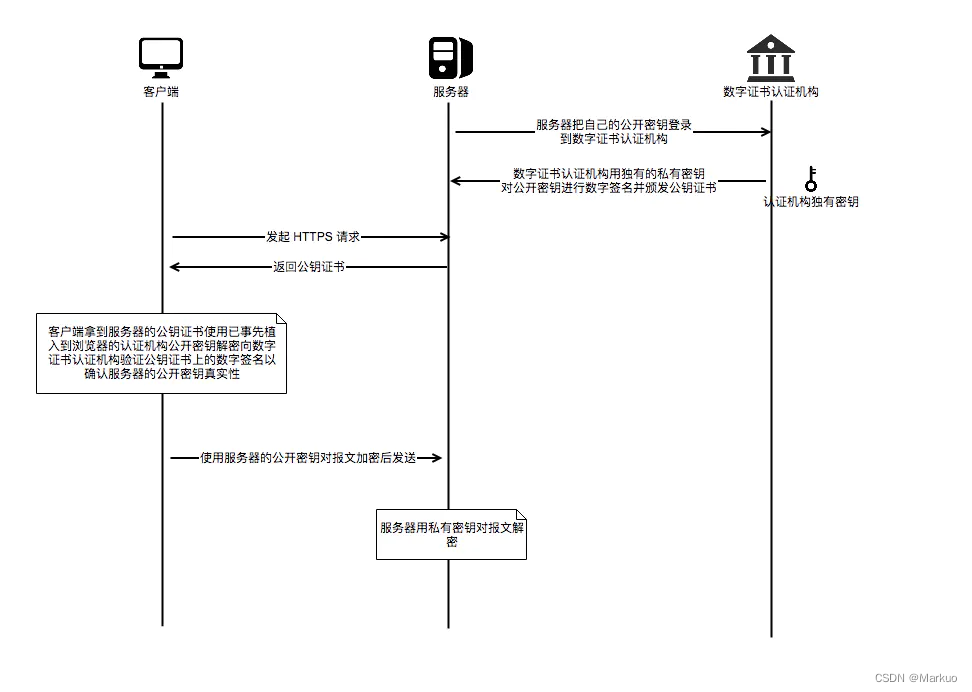
前端面试题 —— 计算机网络(二)
目录 一、POST和PUT请求的区别 二、GET方法URL长度限制的原因 三、页面有多张图片,HTTP是怎样的加载表现? 四、HTTP2的头部压缩算法是怎样的? 五、说一下HTTP 3.0 六、HTTP协议的性能怎么样? 七、数字证书是什么?…...

山东大学机器学习期末2022
接力:山东大学机器学习期末2021 本来是不想写的,因为不想回忆起考试时啥也不会的伤痛,没想到最后给分老师海底捞,心情好了一些,还是一块写完 备考建议:多看ppt,多看ppt,多看ppt 山东…...

FEBC2022|打造VR内容生态闭环 佳创视讯持续加码轻量化内容建设
2月24日,由陀螺科技主办的未来商业生态链接大会作为 2023 癸卯兔年开年率先召开的行业重要影响力盛会在深圳成功召开。今年大会云集了科技、软件、游戏、XR等元宇宙领域的世界500强、上市公司及行业独角兽企业,围绕游戏、元宇宙、XR、数字营销等多项热门…...

Redis常见的数据类型命令
文章目录Redis 常见的数据类型及命令一、常见的NoSQL二、Redis 简介三、key 键的一些操作命令四、Redis的五种基本数据结构1、String(字符串)介绍常用命令1.1 set/get1.2 append1.3 strlen1.4 setex1.5 mset/mget1.6 setrange/getrange1.7 setnx1.8 incr…...

Python3+Selenium3自动化测试-(准备)
最近在学习selenium自动化测试相关的内容,所以将实际准备情况做一记录, # 系统:win10(64位) # 浏览器:Chrome(67.0)、Firefox(61.0)、IE # python版本:3.6.5 # Selenium:3.13.0Selenium简介 Selenium是一…...

VUE的安装和创建
安装node.js 进入node官网进行下载,然后一直下一步。 测试是否安装成功: 命令提示窗下执行:npm -v 若出现版本号,则安装成功。 安装npm源: npm config set registry http://registry.npm.taobao.org 查看:…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...