【算法设计-分治】快速幂与龟速乘
文章目录
- 1. 快速幂
- 2. 龟速乘
- 3. 快速幂取模
- 4. 龟速乘取模
- 5. 快速幂取模优化
1. 快速幂
算法原理:
- 计算 311:
- 311 = (35)2 x 3
- 35 = (32)2 x 3
- 32 = 3 x 3
- 仅需计算 3 次,而非 11 次
- 计算 310:
- 310 = (35)2
- 35 = (32)2 x 3
- 32 = 3 x 3
- 仅需计算 3 次,而非 10 次
算法思路:
- 若指数是偶数,则将底数平方,指数除以 2。
- 若指数是奇数,则将底数平方,指数除以 2,再乘上底数。
算法代码:
typedef unsigned long long uLL;// 快速幂 a^b
uLL power (uLL a, uLL b){uLL r = 1;while (b != 0){if (b & 1) // (b % 2 == 1)r = r * a;b = b >> 1; // (b = b / 2)a = a * a;}return r;
}
举例:
- 初始值:a = 3,b = 11
- 第 1 轮:(11 % 2 == 1)r=1x3=3,b=5,a=32=9
- 第 2 轮:(5 % 2 == 1)r=3x32=33=27,b=2,a=(32)2=34=81
- 第 3 轮:(2 % 2 == 0)r 不变,b=1,a=(34)2=38
- 第 4 轮:(1 % 2 == 1)r=33x38=311,b=0,a=(38)2=316
- 得到 r = 33x38 = 311
2. 龟速乘
算法原理:将其中一个乘数分解成 2 的幂次相加。
12 x a = 23 x a + 21 x a
算法代码:
typedef unsigned long long uLL;// 龟速乘 a*b
uLL mul (uLL a, uLL b){uLL r = 0;while (b != 0){if (b & 1) // (b % 2 == 1)r = r + a;b = b >> 1; // (b = b / 2)a = a + a;}return r;
}
3. 快速幂取模
初等数论中有如下公式:
(a × b) % m = ((a % m) × (b % m)) % m
推广:
(a × b × c…) % m = ((a % m) × (b % m) × (c % m) × … ) % m
(ab) % m = (a × a × a…) % m = ((a % m) × (a % m) × (a % m) × … ) % m
算法代码:
typedef unsigned long long uLL;// 快速幂取模 (a^b) % p
uLL powerMod (uLL a, uLL b, uLL p){uLL r = 1;while (b != 0){if (b & 1) // (b % 2 == 1)r = (r * a) % p;b = b >> 1; // (b = b / 2)a = (a * a) % p;}return r;
}
4. 龟速乘取模
算法原理:(a × b) % m = ((a % m) × (b % m)) % m
算法代码:
// 龟速乘取模 (a*b) % p
uLL mulMod (uLL a, uLL b, uLL p){uLL r = 0;while (b != 0){if (b & 1) // (b % 2 == 1)r = (r + a) % p;b = b >> 1; // (b = b / 2)a = (a + a) % p;}return r;
}
5. 快速幂取模优化
算法原理:注意到快速幂取模算法中的相乘操作可能会超出数据范围,因此可以将相乘操作转化为龟速乘取模。
原理依然是此公式:(a × b) % m = ((a % m) × (b % m)) % m,其中((a % m) × (b % m))即为龟速乘取模。
算法思路:快速幂 + 龟速乘结合。
// 快速幂取模防止爆炸 (a^b) % p
uLL powerModBig (uLL a, uLL b, uLL p){uLL r = 1;while (b != 0){if (b & 1) // (b % 2 == 1)r = mulMod(a, b, p) % p;b = b >> 1; // (b = b / 2)a = mulMod(a, a, p) % p;}return r;
}
相关文章:

【算法设计-分治】快速幂与龟速乘
文章目录1. 快速幂2. 龟速乘3. 快速幂取模4. 龟速乘取模5. 快速幂取模优化1. 快速幂 算法原理: 计算 311: 311 (35)2 x 335 (32)2 x 332 3 x 3仅需计算 3 次,而非 11 次 计算 310: 310 (35)235 (32)2 x 332 3 x 3仅需计算…...

基于新一代kaldi项目的语音识别应用实例
本文是由郭理勇在第二届SH语音技术研讨会和第七届Kaldi技术交流会上对新一代kaldi项目在学术及“部署”两个方面报告的内容上的整理。如果有误,欢迎指正。 文字整理丨李泱泽 编辑丨语音小管家 喜报:新一代Kaldi团队三篇论文均被语音顶会ICASSP-2023接…...
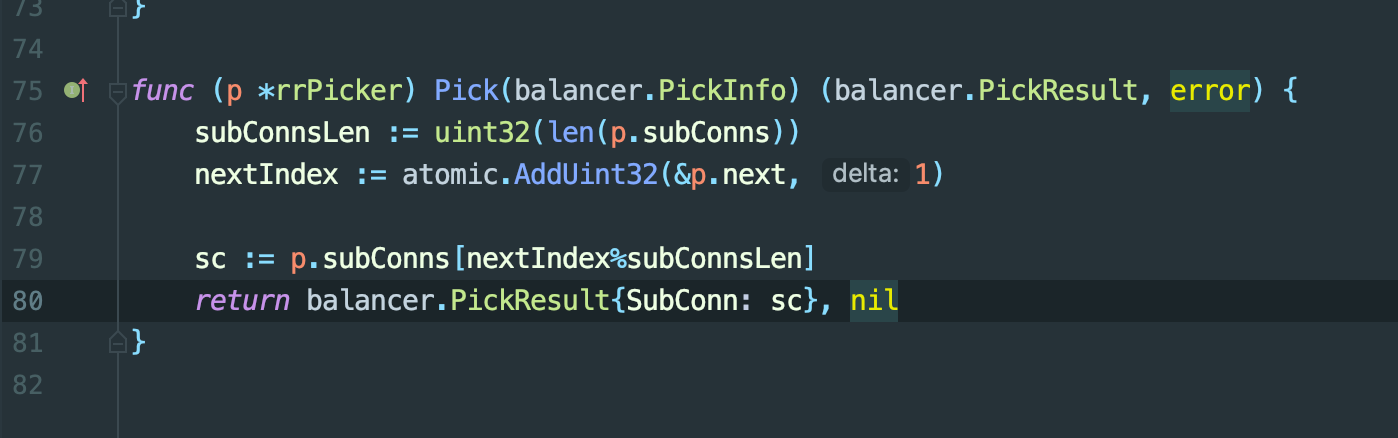
【GO】31.grpc 客户端负载均衡源码分析
这篇文章是记录自己查看客户端grpc负载均衡源码的过程,并没有太详细的讲解,参考价值不大,可以直接跳过,主要给自己看的。一.主要接口:Balancer Resolver1.Balancer定义Resolver定义具体位置为1.grpc源码对解析器(resol…...

PTA L1-058 6翻了(详解)
前言:内容包括:题目,代码实现,大致思路,代码解读 题目: “666”是一种网络用语,大概是表示某人很厉害、我们很佩服的意思。最近又衍生出另一个数字“9”,意思是“6翻了”࿰…...

【Origin科研绘图】如何快速绘制一个折线图 ||【前端特效】爱心篇 之 幸好有你 || 泰坦尼克号——乘客生存与否 预测 || PyCharm使用介绍
🎯作者主页:追光者♂ 🌸个人简介:在读计算机专业硕士研究生、CSDN-人工智能领域新星创作者🏆、2022年CSDN博客之星人工智能领域TOP4🌟、阿里云社区专家博主🏅 【无限进步,一起追光!】 🍎欢迎点赞👍 收藏⭐ 留言📝 🌿本篇,首先是:基于科研绘图工具O…...

一文解读电压放大器(电压放大器原理)
关于电压放大器的科普知识,之前讲过很多,今天为大家汇总一篇文章来详细的讲解电压放大器,希望大家对于电压放大器能有更清晰的认识。电压放大器是什么:电压放大器是一种常用的电子器件,它的主要作用是把输入信号的振幅…...
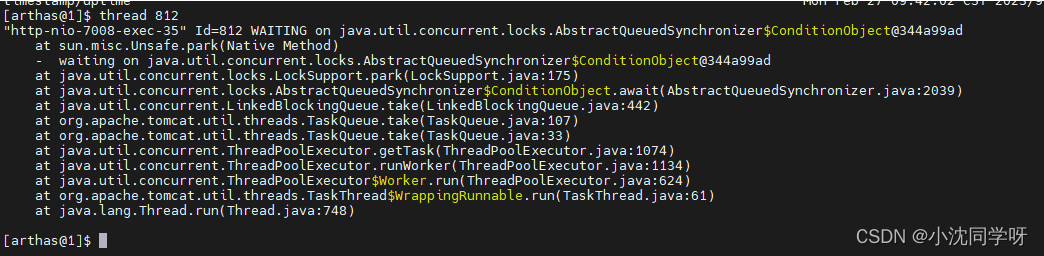
线上监控诊断神器arthas
目录 什么是arthas 常用命令列表 1、dashboard仪表盘 2、heapdump dumpJAVA堆栈快照 3、jvm 4、thread 5、memory 官方文档 安装使用 1、云安装arthas 2、获取需要监控进程ID 3、运行arthas 4、进入仪表盘 5、其他命令使用查看官方文档 什么是arthas arthas是阿…...

@Import注解的原理
此注解是springboot自动注入的关键注解,所以拿出来单独分析一下。 启动类的run方法跟进去最终找到refresh方法; 这里直接看这个org.springframework.context.support.AbstractApplicationContext#refresh方法即可,它下面有一个方法 invoke…...
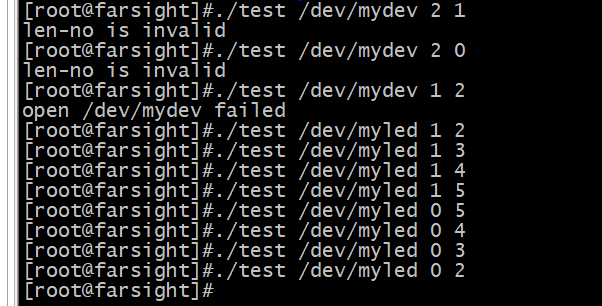
平台总线开发(id和设备树匹配)
目录 一、ID匹配之框架代码 二、ID匹配之led驱动 三、设备树匹配 四、设备树匹配之led驱动 五、一个编写驱动用的宏 一、ID匹配之框架代码 id匹配(可想象成八字匹配):一个驱动可以对应多个设备 ------优先级次低 注意事项…...

TS泛型,原来就这?
一、泛型是什么?有什么作用? 当我们定义一个变量不确定类型的时候有两种解决方式: 使用any 使用any定义时存在的问题:虽然知道传入值的类型但是无法获取函数返回值的类型;另外也失去了ts类型保护的优势 使用泛型 泛型…...
关于算法学习和刷题的建议
大家好,我是方圆。最近花时间学了学算法,应该算是我接触Java以来第一次真正的学习它,这篇帖子我会说一些我对算法学习的理解,当然这仅仅是浅浅的入算法的门,如果想深挖或者是有基础的人想提升自己,我觉得这…...
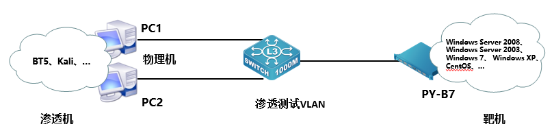
2023年“网络安全”赛项浙江省金华市选拔赛 任务书
2023年“网络安全”赛项浙江省金华市选拔赛 任务书 任务书 一、竞赛时间 共计3小时。 二、竞赛阶段 竞赛阶段 任务阶段 竞赛任务 竞赛时间 分值 第一阶段单兵模式系统渗透测试 任务一 Windows操作系统渗透测试 任务二 Linux操作系统渗透测试 任务三 网页渗透 任务四 Linux系统…...

http协议简介
http 1.简介 超文本传输协议(HTTP,HyperText Transfer Protocol)是互联网上应用最为广泛的一种网络协议。所有的WWW文件都必须遵守这个标准。设计HTTP最初的目的是为了提供一种发布和接收HTML页面的方法。1960年美国人Ted Nelson构思了一种通过计算机处…...

CSDN 第三十一期竞赛题解
第二次参加 总分77.5,主要是在最后一题数据有误,花费了巨量时间… 参加的另一次比赛最后一道题目也出现了一点问题,有点遗憾。 题解 T1:最优利润值 你在读的经营课程上,老师布置了一道作业。在一家公司的日常运营中&…...
)
EM_ASM系列宏定义(emscripten)
2.5 EM_ASM系列宏很多编译器支持在C/C代码直接嵌入汇编代码,Emscripten采用类似的方式,提供了一组以“EM_ASM”为前缀的宏,用于以内联的方式在C/C代码中直接嵌入JavaScript代码。2.5.1 EM_ASMEM_ASM使用很简单,只需要将欲执行的Ja…...

Batchnorm和Layernorm的区别
在深度学习训练中,我们经常会遇到这两个归一化操作,他们之间有什么区别呢?我们来简单介绍一下: BatchNorm: 在深度学习训练的时候我们的数据如果没有经过预处理,有可能会出现梯度消失或者梯度爆炸的情况&…...

高级前端面试题汇总
iframe 有那些优点和缺点? iframe 元素会创建包含另外一个文档的内联框架(即行内框架)。 优点: 用来加载速度较慢的内容(如广告)可以使脚本可以并行下载可以实现跨子域通信 缺点: iframe 会…...
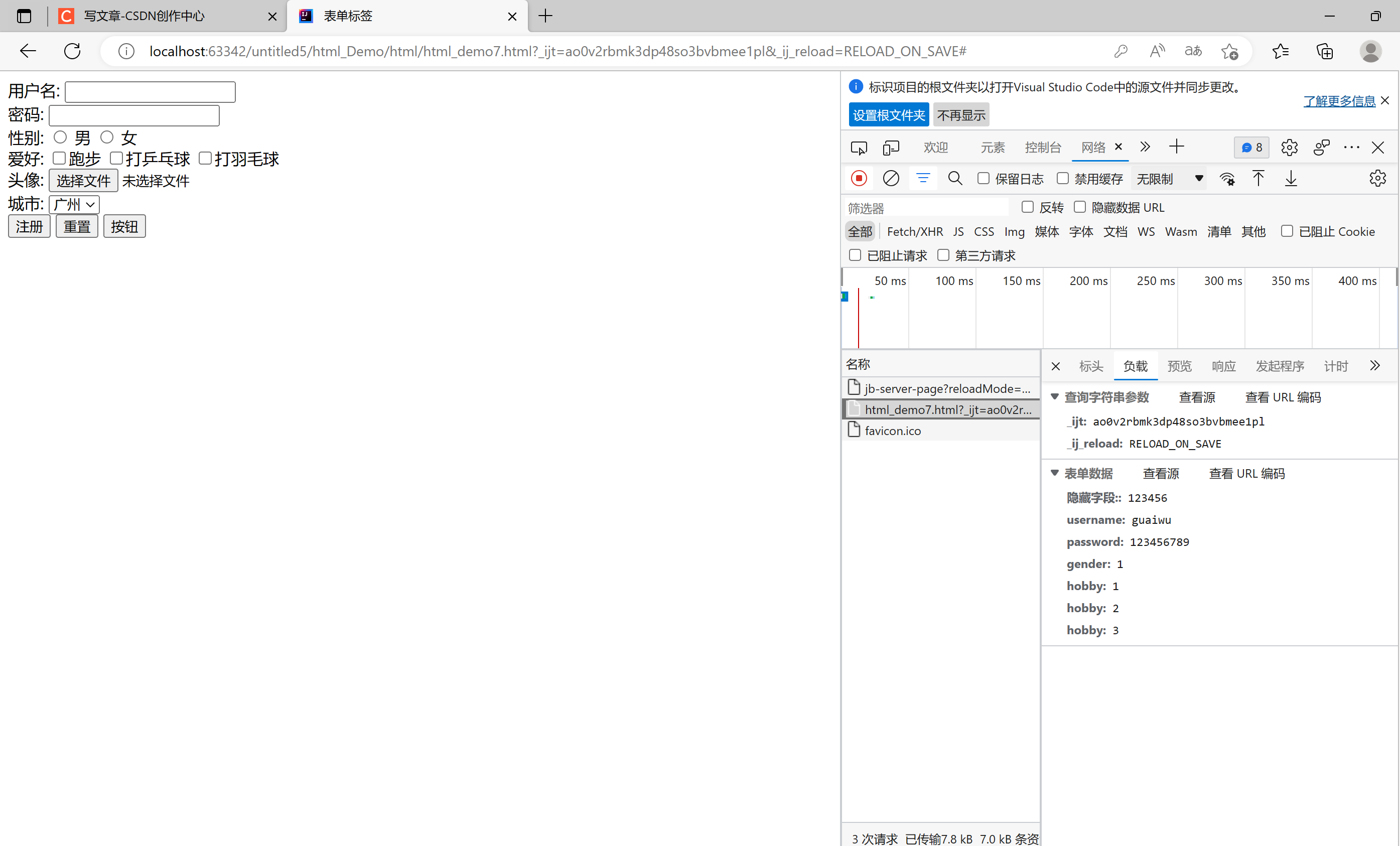
HTML#5表单标签
一. 表单标签介绍表单: 在网页中主要负责数据采集功能,使用<form>标签定义表单表单项: 不同类型的input元素, 下拉列表, 文本域<form> 定义表单<input> 定义表单项,通过typr属性控制输入形式<label> 为表单项定义标注<select> 定义下拉列表<o…...

ONNX可视化与编辑工具
ONNX可视化与编辑工具netrononnx-modifier在模型部署的过程中,需要使用到ONNX模型,下面给大家推荐两个ONNX可视化与编辑工具,其中,netron仅支持模型的可视化,onnx-modifier支持ONNX的可视化与编辑。 netron Netron是…...
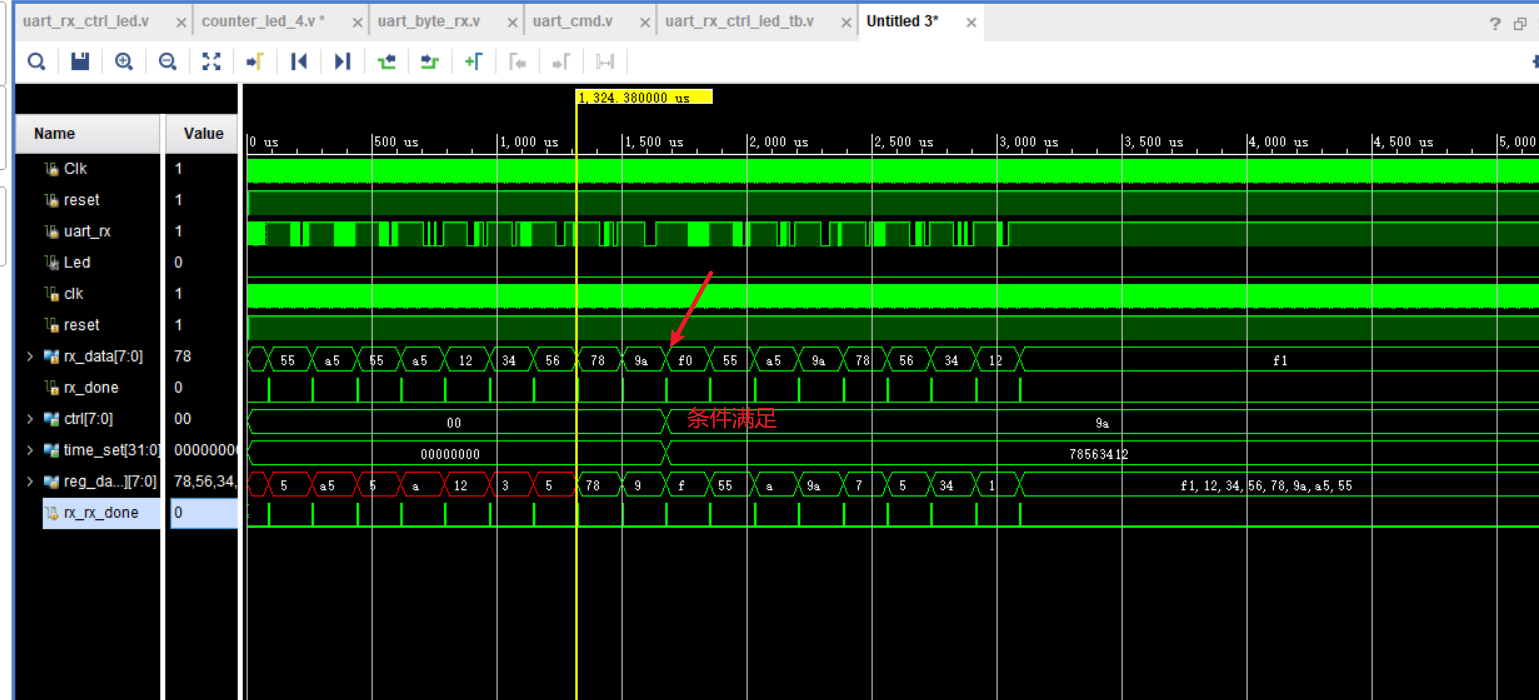
Verilog 学习第五节(串口接收部分)
小梅哥串口部分学习part2 串口通信接收原理串口通信接收程序设计与调试巧用位操作优化串口接收逻辑设计串口接收模块的项目应用案例串口通信接收原理 在采样的时候没有必要一直判断一个clk内全部都是高/低电平,如果采用直接对中间点进行判断的话,很有可能…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...

SpringCloud优势
目录 完善的微服务支持 高可用性和容错性 灵活的配置管理 强大的服务网关 分布式追踪能力 丰富的社区生态 易于与其他技术栈集成 完善的微服务支持 Spring Cloud 提供了一整套工具和组件来支持微服务架构的开发,包括服务注册与发现、负载均衡、断路器、配置管理等功能…...
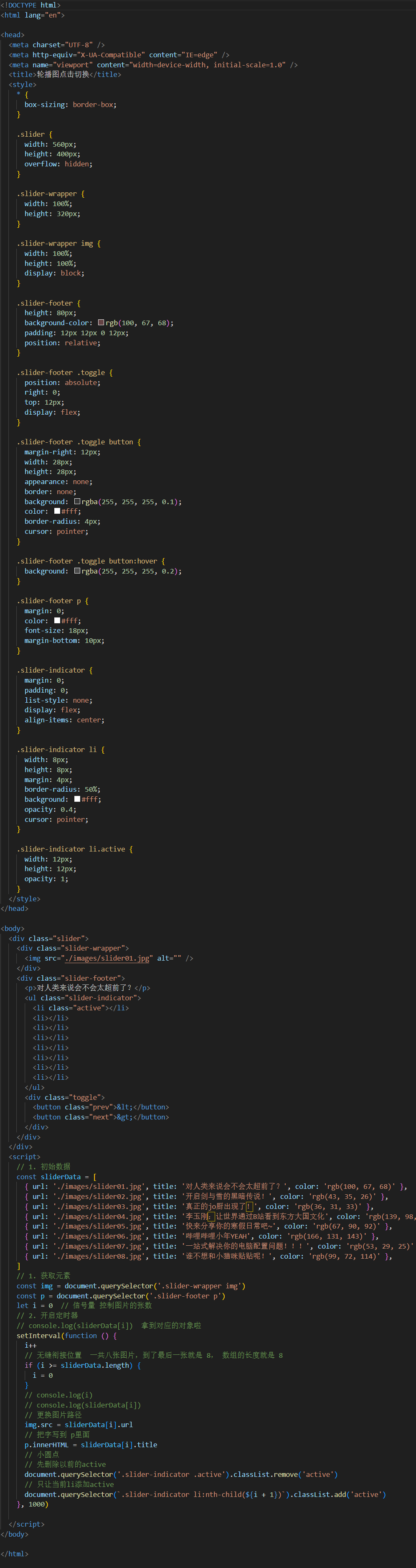
Web APIS Day01
1.声明变量const优先 那为什么一开始前面就不能用const呢,接下来看几个例子: 下面这张为什么可以用const呢?因为复杂数据的引用地址没变,数组还是数组,只是添加了个元素,本质没变,所以可以用con…...
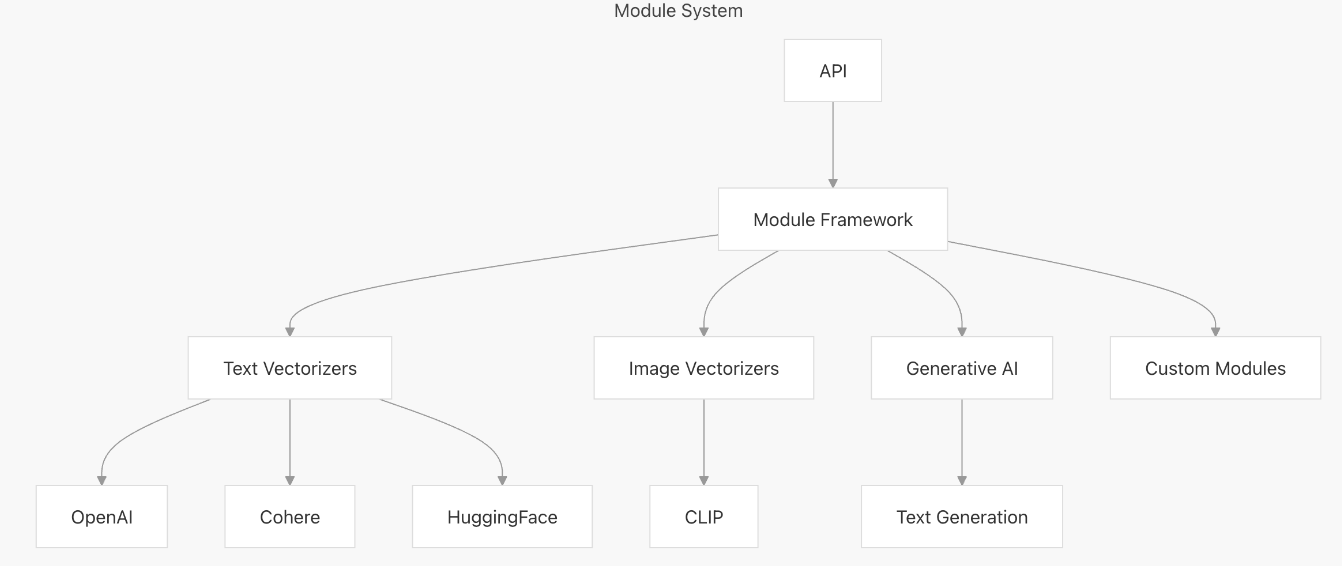
【向量库】Weaviate概述与架构解析
文章目录 一、什么是weaviate二、High-Level Architecture1. Core Components2. Storage Layer3. 组件交互流程 三、核心组件1. API Layer2. Schema Management3. Vector Indexing3.1. 查询原理3.2. 左侧:Search Process(搜索流程)3.3. 右侧&…...
