用欧拉路径判断图同构推出reverse合法性:1116T4
http://cplusoj.com/d/senior/p/SS231116D
假设我们要把 a a a 变成 b b b,我们在 a i a_i ai 和 a i + 1 a_{i+1} ai+1 之间连边, b b b 同理,则 a a a 能变成 b b b 的充要条件是两图 A , B A,B A,B 同构。
必要性显然,因为无论如何reverse都不会改变图的形态。我们现在要证明的是图的任意欧拉路径都可以通过reverse构造出来。
考虑第一个 a i ≠ b i a_i\neq b_i ai=bi 的位置 i i i,设 x = b i , y = b i − 1 = a i − 1 x=b_i,y=b_{i-1}=a_{i-1} x=bi,y=bi−1=ai−1。在图同构是必然存在一个 a k = x a_k=x ak=x,且 a k − 1 a_{k-1} ak−1 或 a k + 1 a_{k+1} ak+1 其中一个等于 y y y。(注意 A , B A,B A,B 同构)
如果 a k + 1 = y a_{k+1}=y ak+1=y,我们直接reverse即可。如果 a k − 1 = y a_{k-1}=y ak−1=y,我们只需要考虑 ( x , y ) (x,y) (x,y) 这条边在 A A A 中是不是桥就行。因为在 B B B 中一定不是桥(注意到 y y y 必然出现两次)
因为如果在 A A A 中是桥, B B B 中不是,说明 A , B A,B A,B 不同构,和我们的前提冲突。
如果在 A A A 中不是桥,说明对于这条边来说 A , B A,B A,B 同构,说明一定存在 i ≤ l ≤ k − 1 , r > k + 1 i\le l \le k-1,r>k+1 i≤l≤k−1,r>k+1 满足 a l = a r a_l=a_r al=ar。我们直接按 [ l , r ] [l,r] [l,r] reverse即可。因此一定可以构造
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>using namespace std;struct xorShift128Plus {unsigned long long k1, k2;unsigned long long gen() {register unsigned long long k3 = k1, k4 = k2;k1 = k4;k3 ^= k3 << 23;k2 = k3 ^ k4 ^ (k3 >> 17) ^ (k4 >> 26);return k2 + k4;}int gen(int w) {return gen()%w;}
}rnd;const int S=5000005;
#define pb push_back
#define fi first
#define se secondint n, a[S], t[S], k, i, tot;
bool b[S];
int ans[S];
vector<pair<int, int> >G[S]; void dfs(int x) {for(; t[x]<G[x].size(); ){auto p=G[x][t[x]]; ++t[x]; if(b[p.se]) continue; int y=p.fi; b[p.se]=1; dfs(y); }ans[++tot]=x;
}void cun(int x, int y) {G[x].pb({y, ++k}); G[y].pb({x, k});
}int main()
{freopen("life.in","r",stdin);freopen("life.out","w",stdout);#ifdef LOCALfreopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);#endifint t;scanf("%d%d",&n,&t);if(t==0) for(int i=1;i<=n;i++) scanf("%d",&a[i]);else{int ra;scanf("%d%llu%llu",&ra,&rnd.k1,&rnd.k2);for(int i=1;i<=n;i++) a[i]=rnd.gen(ra)+1;}// cun(n+1, a[1]); cun(n+2, a[n]); for(i=1; i<n; ++i) cun(a[i], a[i+1]); for(i=1; i<=n+2; ++i) {sort(G[i].begin(), G[i].end());
// reverse(G[i].begin(), G[i].end()); }dfs(a[1]); reverse(ans+1, ans+n+1); /*code here*/if(t==0){for(int i=1;i<=n;i++) printf("%d ",ans[i]);printf("\n");}else{int bse=1919839,p=1000000007;int mul=1,res=0;for(int i=1;i<=n;i++,mul=1ll*mul*bse%p) res=(res+1ll*ans[i]*mul%p)%p;printf("%d\n",res);}return 0;
}
相关文章:

用欧拉路径判断图同构推出reverse合法性:1116T4
http://cplusoj.com/d/senior/p/SS231116D 假设我们要把 a a a 变成 b b b,我们在 a i a_i ai 和 a i 1 a_{i1} ai1 之间连边, b b b 同理,则 a a a 能变成 b b b 的充要条件是两图 A , B A,B A,B 同构。 必要性显然࿰…...

高阶数据结构---树状数组
文章目录 楼兰图腾一个简单的整数问题 一个简单的整数问题2谜一样的牛 一、楼兰图腾OJ链接 二、一个简单的整数问题OJ链接 三、一个简单的整数问题2OJ链接 四、谜一样的牛OJ链接...

如何保护PayPal账户安全:防止多个PayPal账号关联?
PayPal是一家全球领先的在线支付平台,已经成为全球最受欢迎的在线支付工具之一,广泛应用于电子商务、跨境交易和个人之间的付款,很多跨境卖家的支付平台都会选择PayPal。PayPal支持全球多个国家和20多种货币在线支付,并且能即时收…...

关于 Spring :松耦合、可配置、IOC、AOP
关于 Spring :松耦合、可配置、IOC、AOP 文章目录 关于 Spring :松耦合、可配置、IOC、AOP一、关于 Spring1、概述2、Spring 的“松耦合”体现在哪3、Spring 的“可配置”体现在哪4、Spring 的 IOC 容器的主要作用5、Spring 的 AOP 容器的主要作用 一、关…...

pytorch tensor数据类型转换为python数据
一、item() input: x torch.tensor([1.0]) x.item()output: 1.0二、tolist() input: a torch.randn(2, 2) a.tolist() a[0,0].tolist()output: [[0.012766935862600803, 0.5415473580360413],[-0.08909505605697632, 0.7729271650314331]]0.012766935862600803...
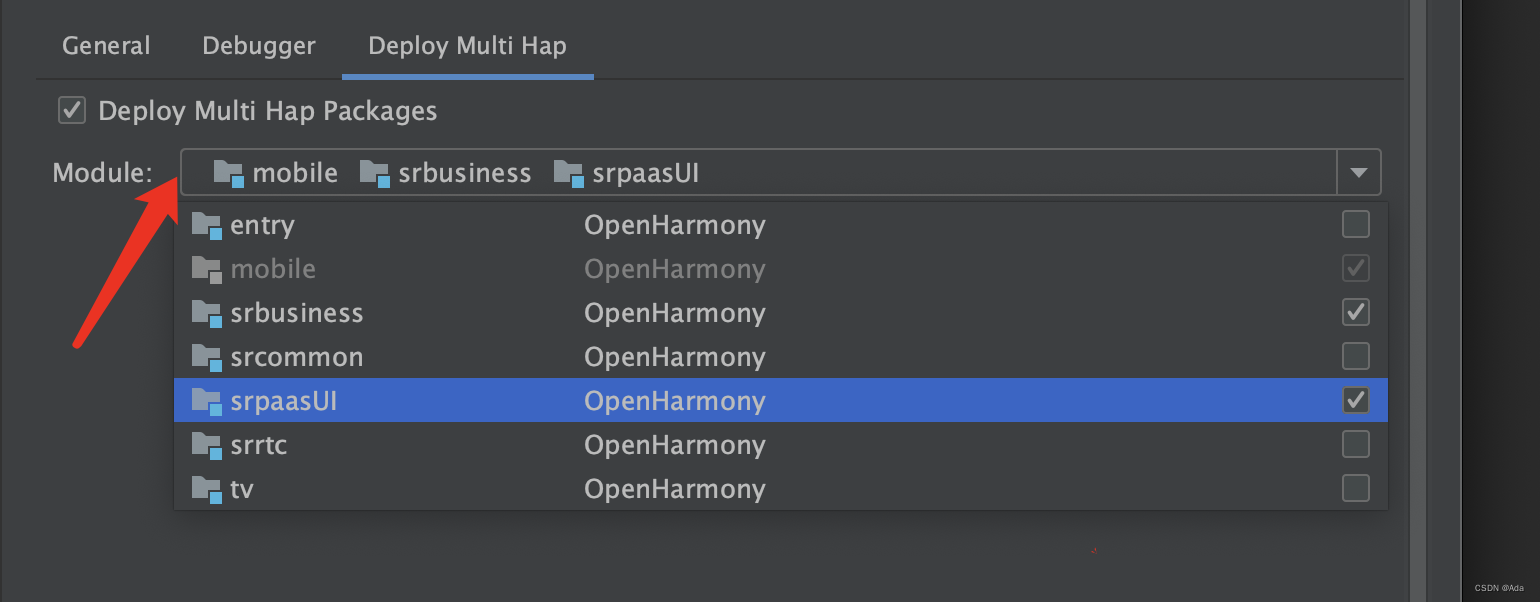
HarmonyOS开发:动态共享包的依赖问题
一、共享包的依赖方式 在需要依赖的模块包目录下oh-package.json5文件中添加依赖: "dependencies": {"ohos/srpaasUI": "file:../../srpaasUI","ohos/srbusiness": "file:../../feature/srbusiness"} 引入之后…...

中睿天下加入中关村华安关键信息基础设施安全保护联盟
近日,中睿天下正式加入中关村华安关键信息基础设施安全保护联盟,成为其会员单位。 中关村华安关键信息基础设施安全保护联盟是由北京市科学技术委员会、中关村科技园区管理委员会指导支持,经北京市民政局批准,于2023年8月正式注册…...

【c++STL算数仿函数,关系仿函数,逻辑仿函数】
文章目录 C STL中的算数、关系和逻辑仿函数1. 算数仿函数2. 关系仿函数3. 逻辑仿函数 C STL中的算数、关系和逻辑仿函数 STL(Standard Template Library)是C标准库的一部分,提供了许多强大的工具和功能,其中包括仿函数࿰…...
产品经理的能力模型是什么?
一个产品的成功需要团队成员利用自己的技能共同合作完成。作为团队的核心和产品的主导者,产品经理需要具备一定的能力模型,以更好地完成工作。下面从五个方面进行解答。 首先,产品经理需要具备需求分析的能力。需求是用户在特定场景下产生的欲…...

缓存和DB一致性
读操作,一般是先查询缓存,查询不到再查询数据库,最后回写进缓存。 写操作,究竟是先删除(更新)缓存,再更新数据库,还是先更新数据库,再删除(更新)缓存呢? 1、给缓存设置过期时间 适用…...

netty websockt之断连重试
断连重试有以下两点考虑: 1、连接异常,比如网络抖动导致连接失败; 2、连接过程中断开连接重试; 主要用到两个工具类: ChannelFutureListener监听ChannelFuture..isSuccess(); ChannelInboundHandlerAd…...

【Gateway】基于ruoyi-cloud-plus项目,gateway局部过滤器和过滤返回以及集成nacos
1.使用Gateway路由转发 1.1标题引入依赖 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-gateway</artifactId></dependency>1.2添加YML配置 spring:cloud:gateway:# 打印请求日志(自定义)…...

mysql -mmm
MMM(Master-Master replication manager for MvSQL,MySQL主主复制管理器) 是一套支持双主故障切换和双主日常管理的脚本程序。MMM 使用 Perl 语言开发,主要用来监控和管理 MySQL Master-Master (双主)复制&…...
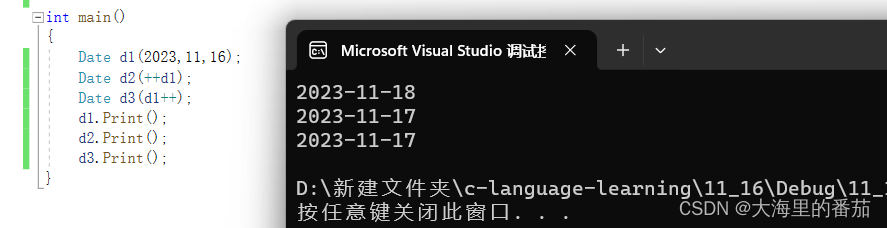
C++初阶 类和对象(下)
目录 一、拷贝构造函数 1.1 什么是拷贝构造函数? 1.2 为什么得是引用? 1.3 使用拷贝构造函数 1.4 拷贝构造函数有什么用? 二、运算符重载 2.1 什么是运算符重载? 2.2 尝试前须知 2.3 常见运算符重载 2.3.1运算符重载 …...
使用Postman进行压力测试
1.打开Postman新建测试接口 2.点击右边保存,选择一个文件集合,如果没有就创建,然后保存 就是这个东西,这里不便展示出来,压力测试需要在文件夹里面进行 3.选择要测试的接口,iterations 表示请求发起次数&a…...

AI视频检索丨历史视频标签化,助力重要事件高效溯源
随着科技的不断发展,安全监控已成为我们生活中不可或缺的一部分。当发生盗窃、人员走失、安全事故等重要事件时,常常需要通过查看视频回放了解事情经过,为解决问题提供证据或指明查找方向。但是,人工查看视频回放往往费时费力&…...

【前段基础入门之】=>CSS3新特性 响应式布局
文章目录 概念媒体查询媒体类型媒体特性媒体运算符 概念 所谓对响应式布局方案的理解,众说纷纭,核心点就是同一套代码在不同尺度屏幕下的布局呈现方式的不同 社区中有很多人分享,并列出了多种实现响应式布局的方案,比如【 rem&…...

【Java 进阶篇】JQuery 遍历:发现元素的魔法之旅
欢迎来到 JQuery 的奇妙世界,一个充满活力和灵感的地方。在这个世界里,我们将一起探讨 JQuery 的遍历功能,这是一个让你轻松发现和操作网页元素的神奇工具。无需太多前端经验,只要有一颗探险的心,你就能在 JQuery 遍历…...

合肥数字孪生赋能工业制造,加速推进制造业数字化转型
聚焦国家战略需求和先进制造业发展方向,加快数字化发展战略部署,数字孪生、工业互联网、工业物联网已被广泛认为是工业革命的新引擎。合肥数字孪生正在推动工业制造从制造转向智造。通过数字化建模和仿真的方式,优化设计、生产、质量管理、供…...
Linux发展史与环境安装
Linux发展史与环境安装 一、Linux发展史推动技术进步的基本模式理解操作系统的发展理解Linux操作系统的发展 一、Linux的环境安装 一、Linux发展史 Linux和window XX其实都是一样的,定位:操作系统,企业内部,要给用户提供“互联网…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
