数据结构-考研难点代码突破(C++实现树型查找 - B树插入与遍历,B+树基本概念)
数据结构(C++)[B树(B-树)插入与中序遍历,效率分析]、B+树、B*树、B树系列应用
文章目录
- 1. B树
- B树的插入与删除流程
- 2. B+树(MySQL)
- 3. B+树与B树对比
- 4. C++实现B树插入,中序遍历
1. B树
B树类似于二叉排序树,B树可以理解为多叉排序树。
B树和二叉排序树相类似,查找效率取决于树的高度。
因为二搜索树每个节点只能存一个数据。而B树每一个节点可以储存多个值(这些值在这个节点内部按照顺序排序)。
所以一般情况下,B树的高度小于搜索二叉树,效率高。
注意:如果B树的每个节点只保存一个数据,B树就退化为搜索二叉树
- 所以为了避免这种情况,规定除了根节点外,任意m叉树中每一个节点规定至少有[m/2]向上取整,个分叉,至少含有[m/2]-1个数据。
- 多叉树在插入后,高度退化为线性查找,所以规定m叉树任意一个节点的高度相同。
B树的定义:
B树,又称多路平衡查找树,B树中所有结点的孩子个数的最大值称为B树的阶,通常用m表示。一棵m阶B树或为空树,或为满足如下特性的m叉树:
- 树中每个结点至多有m棵子树,即至多含有m-1个关键字。
- 若根结点不是终端结点,则至少有两棵子树(绝对平衡)。
- 除根结点外的所有非叶结点至少有「m/2]棵子树,即至少含有[m/2]-1个关键字。
- 所有的叶结点都出现在同一层次上,并且不带信息(可以视为外部结点或类似于折半查找判定树的查找失败结点,实际上这些结点不存在,指向这些结点的指针为空)
- 每个非叶结点的结构为:(n,A0,K1,A1,K2,A2,… ,Kn,An)其中,Ki(1≤i≤n)为关键字,且Ki<Ki+1(1≤i≤n-1)。Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。n为结点中关键字的个数,满足ceil(m/2)-1≤n≤m-1。(关键字按照升序排列,同时保证A0<K1<A1<K2<A2)(多叉搜索树)
需要注意的是计算B树的高度不包括失败节点层
含有n个关键字的m阶B树
最小高度:每一个节点填满关键字,每一个节点放m-1个关键字n≤(m-1)(1+m+m^2+...+m^(h-1)),最小高度为logm(n+1)
最大高度:每一个节点储存最小关键字(分叉数最小),根节点最小有2个分叉,其他节点最小有m/2个分叉第一层最少有1个节点,第二次有两个,第三次有2(m/2),第四层有2(m/2)*(m/2)...第n层2(m/2)^(h-2)第n+1层是失败节点,最少有2(m/2)^(h-1)个节点。而n个关键字的B树一定有n+1个叶节点,失败节点所以n+1≥2(m/2)^(h-1),求解h即可得出最大高度。

B树的插入与删除流程
B树的插入:
连续插入key,在插入key后,若导致原结点关键字数超过上限。则从中间位置_([m/2])将其中的关键字分为两部分。
左部分包含的关键字放在原结点中,右部分包含的关键字放到新结点中,中间位置[m/2]的结点插入原结点的父结点
eg:三阶B树插入关键字(53, 139, 75, 49, 145, 36, 50, 47, 101)
节点最多保存2个关键字,最少保存1个关键字。根节点单独看
- 根节点最多可以保存2个关键字,为了简化插入操作,开辟三个关键字大小,当插入后发现已经满了时再进行分裂。同时多开辟一个空间也有助于在插入时进行排序。
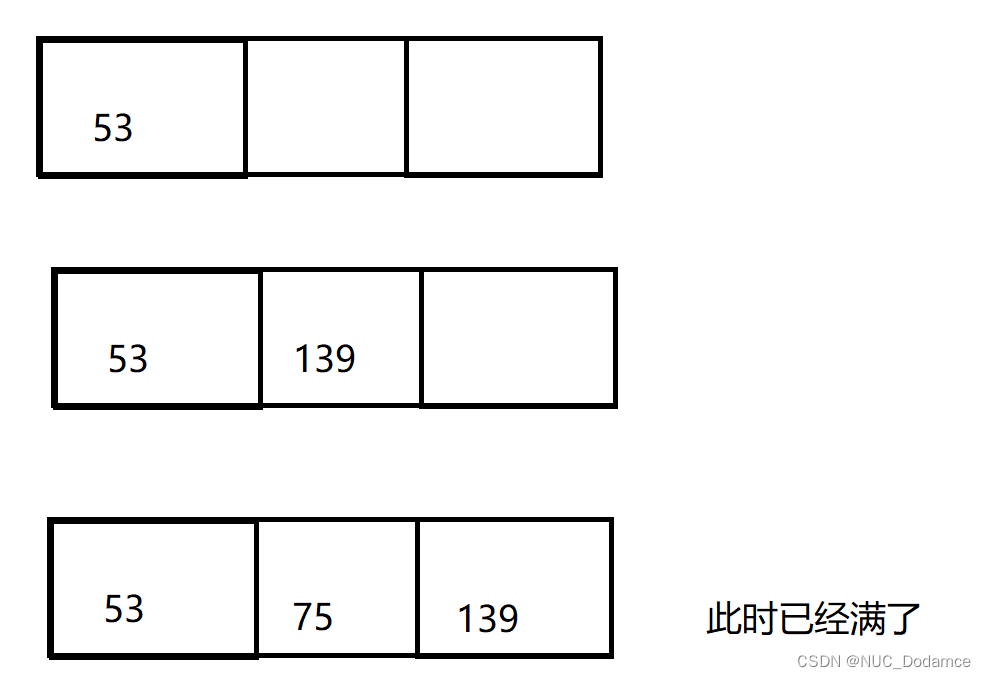
- 如果节点满了,分裂右边一半关键字个数的一般给兄弟节点。提取中位数给父亲,没有父亲就创建新的根节点
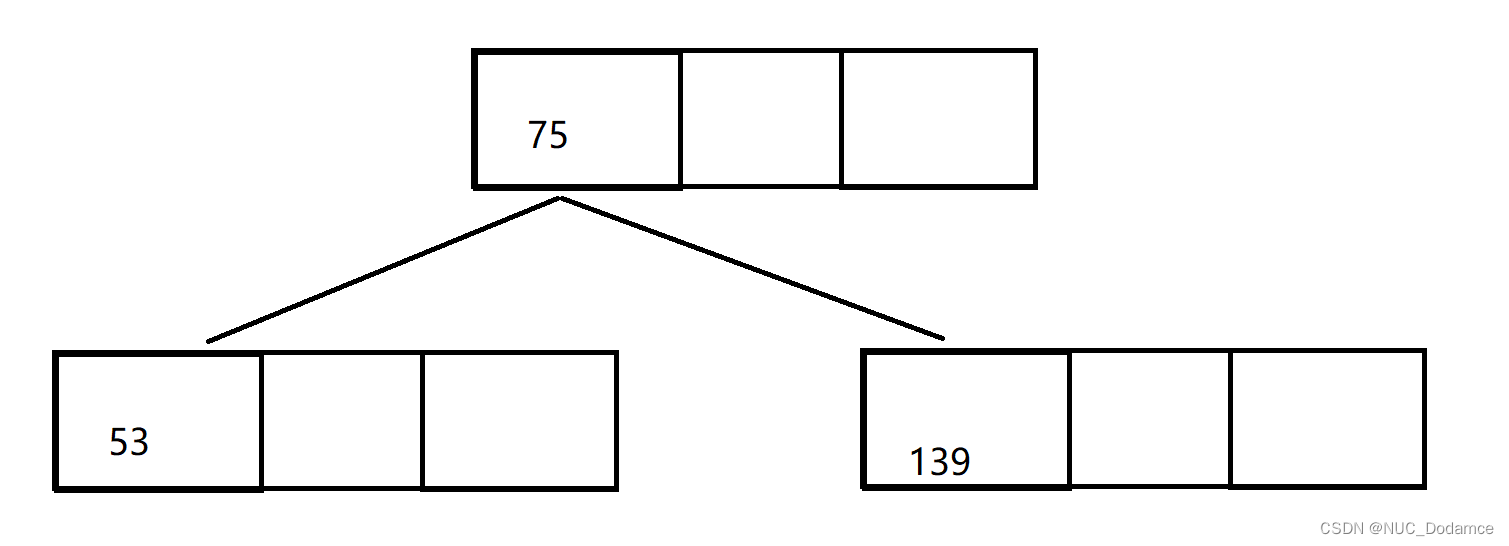
- 继续插入49等后续关键字。
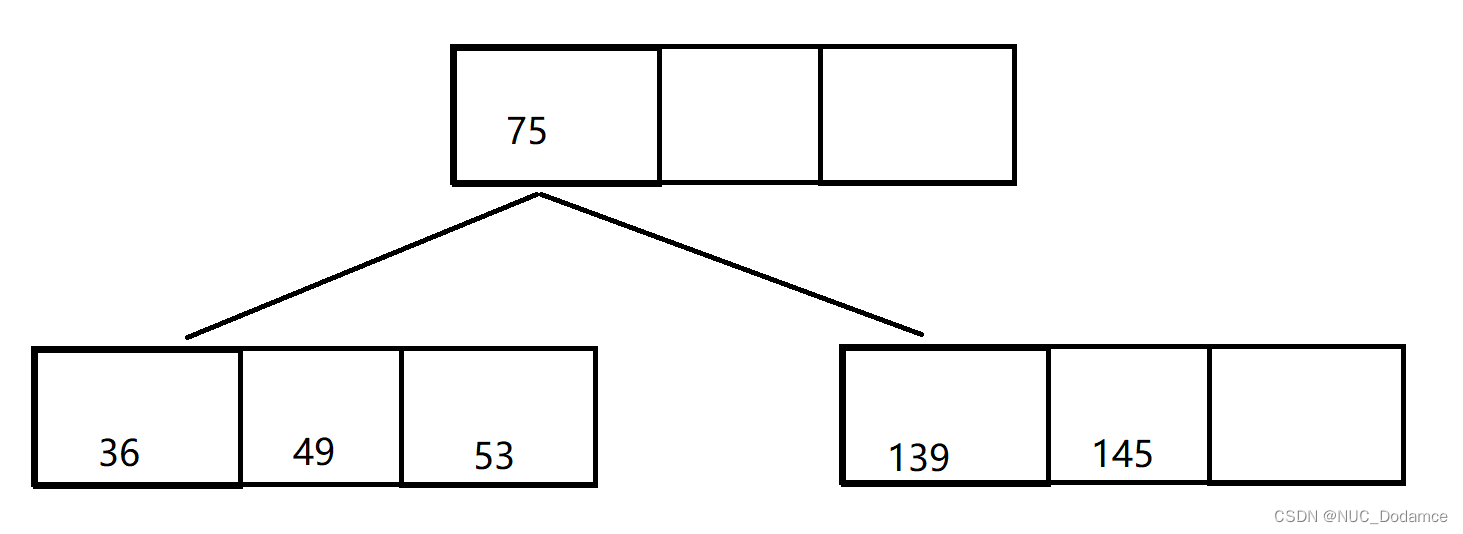
此时节点又满了,需要进行分裂。
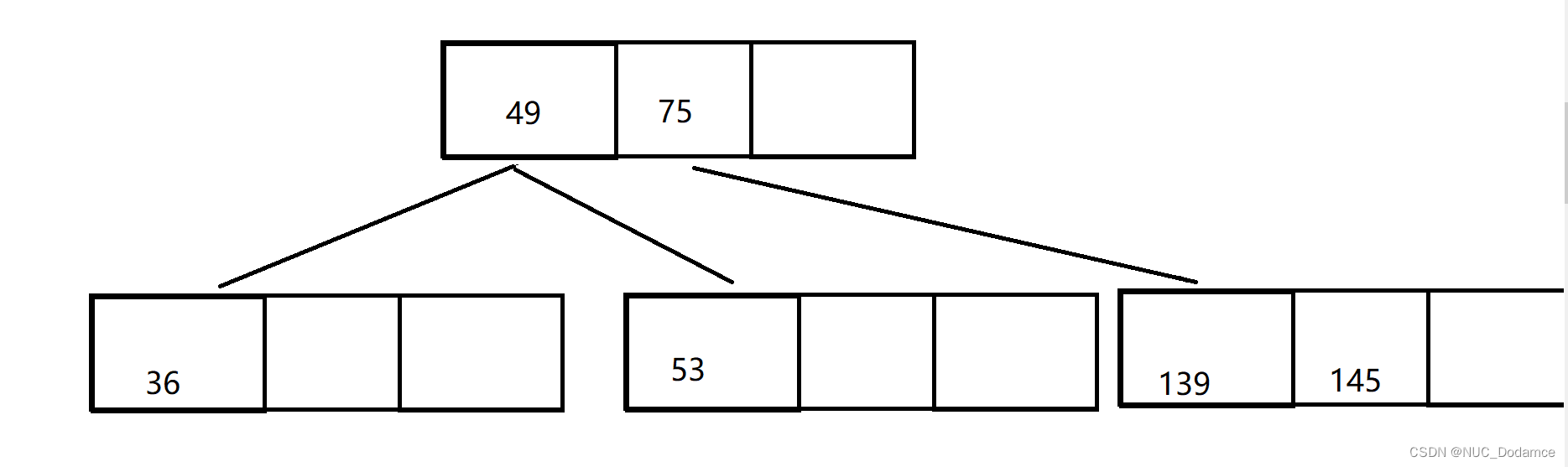
- 继续插入50和47这两个关键字。
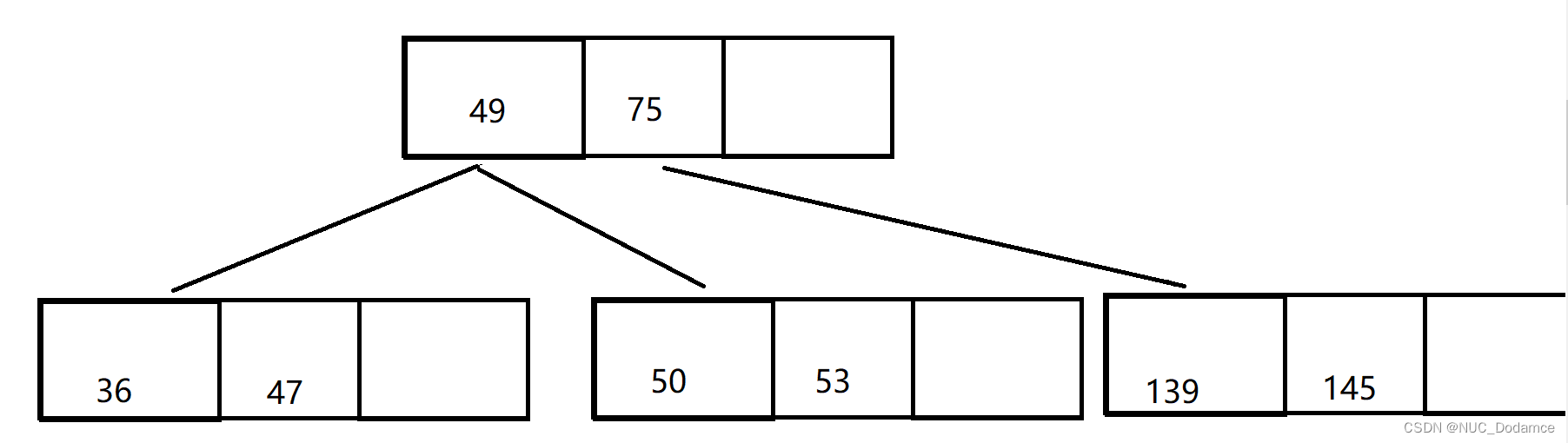
- 最后插入101,导致叶子节点满,需要进行分裂
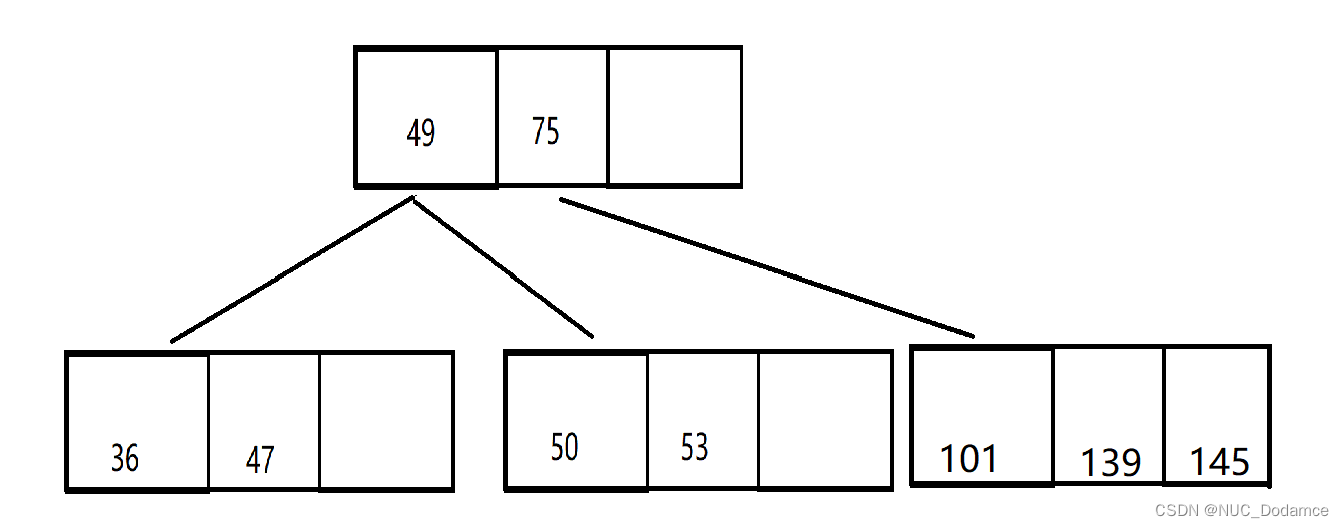
这次分裂会导致两次连续分裂
第一次分裂导致根节点满
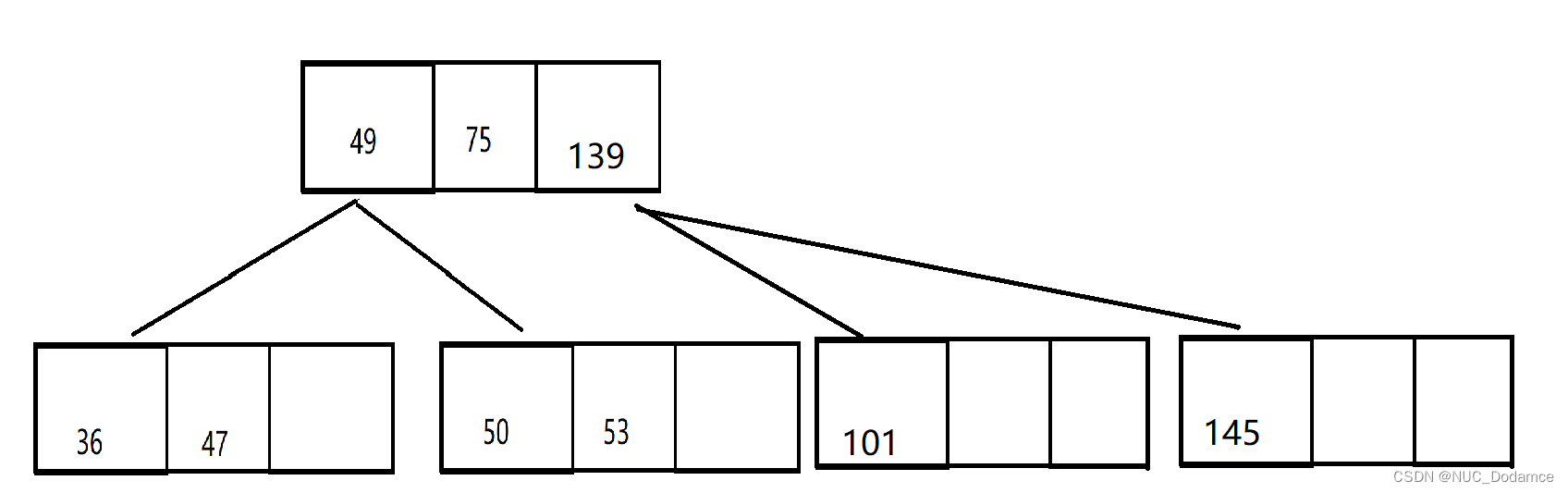
继续分裂根节点,产生新的根节点
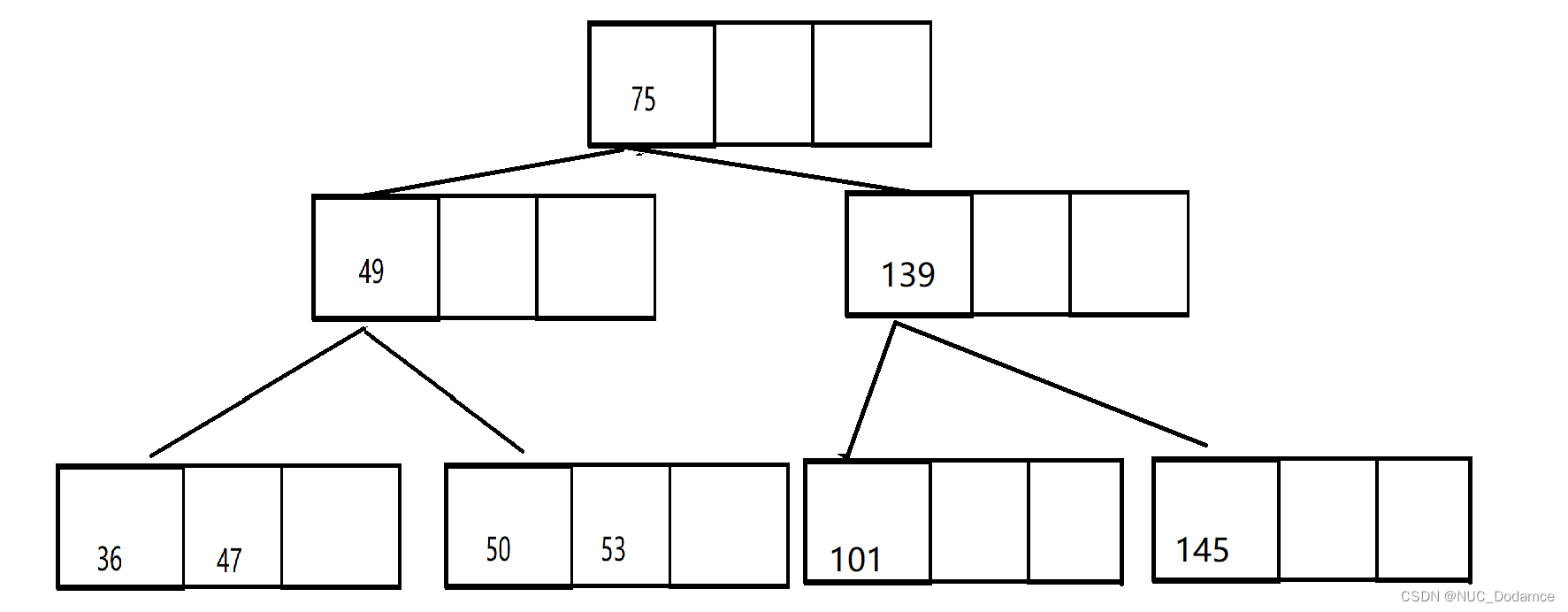
插入完毕
特点
- B树天然平衡,B树是先横向扩展,再竖直生长。所以B树天然平衡
- 新插入的节点一定在叶子插入,叶子节点没有孩子,不影响关键字和孩子的关系
- 叶子节点满了,分裂出一个兄弟,提取中位数,向父亲插入一个值和孩子
- 根节点分裂会增加一层
- 对于B树的每一个节点,这个节点的孩子个数比关键字个数多一个。
B树的删除:
-
若被删除关键字在终端节点,则直接删除该关键字(要注意节点关键字个数是否低于下限[m/2] -1)
-
若被删除关键字在非终端节点,则用直接前驱或直接后继来替代被删除的关键字。这样就转化为对终端节点的删除了。
直接前驱:当前关键字左侧指针所指子树中“最右下”的元素
特别注意:如果删除终端节点到下线,这是需要进行分类处理
-
这个节点的兄弟节点可以借出一个元素时:
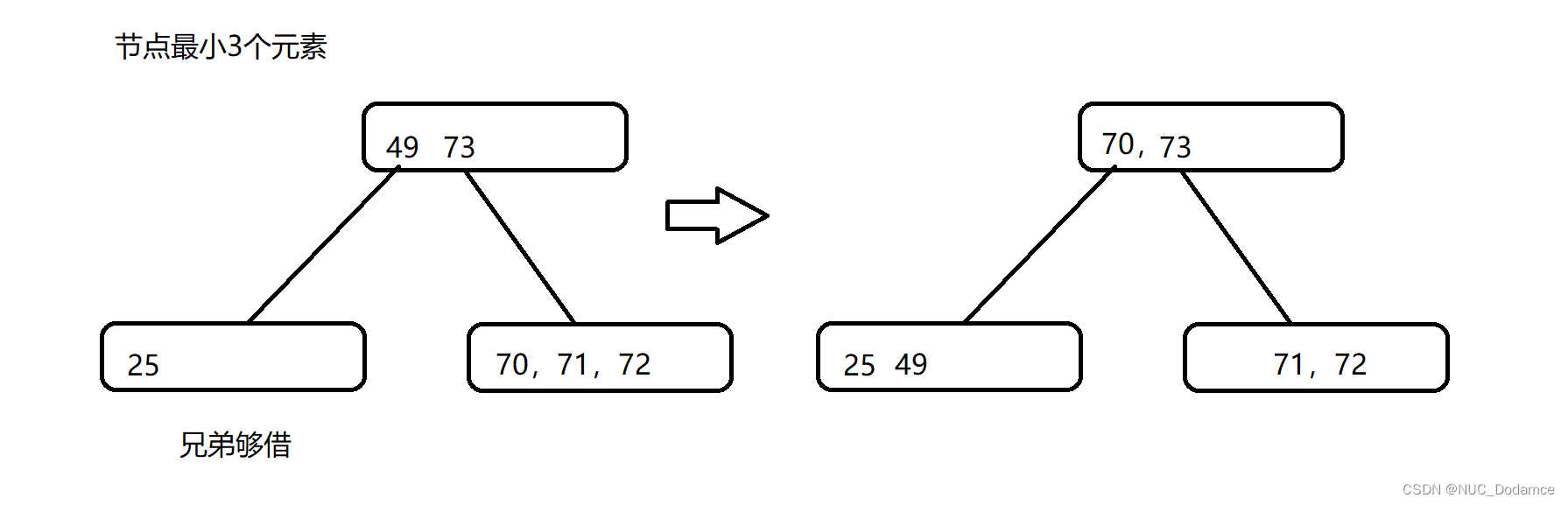

-
兄弟节点不够借用:这个节点和兄弟节点进行合并
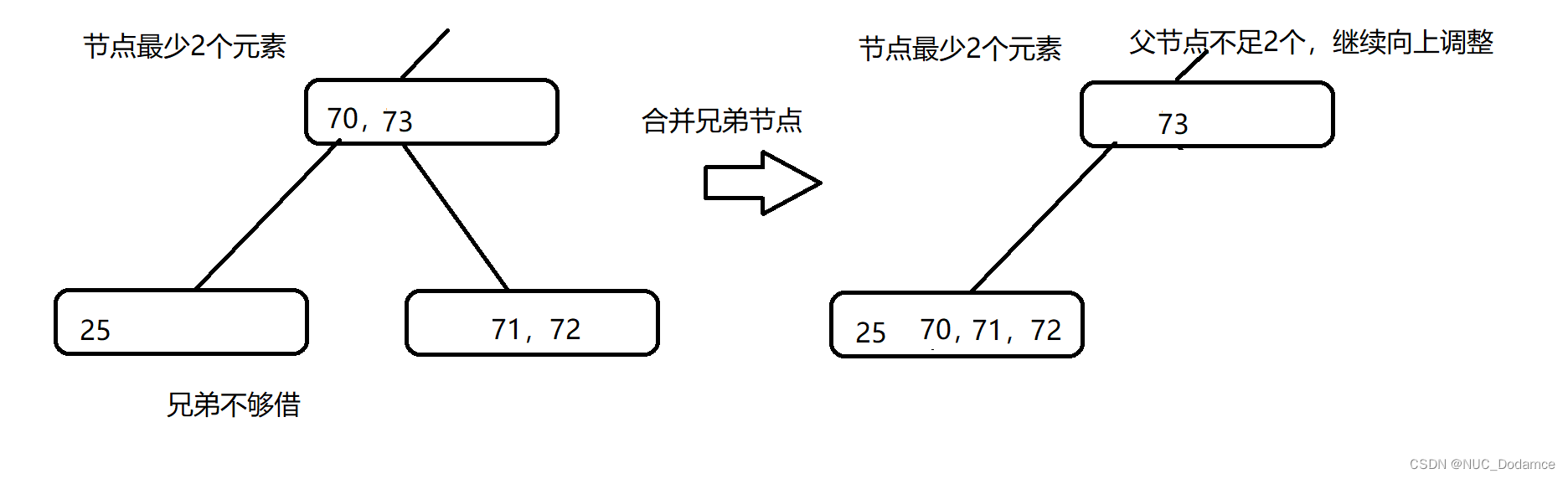
2. B+树(MySQL)
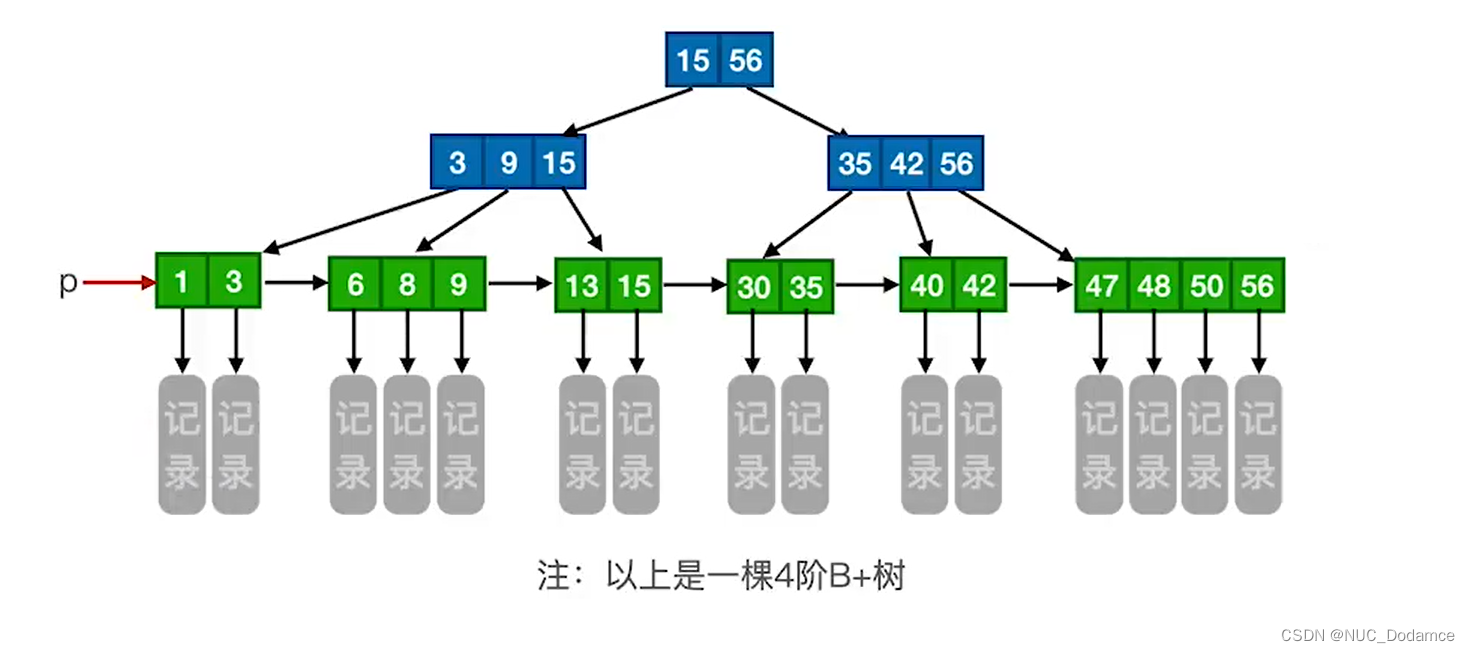
类似于分块查找,一棵m阶的B+树需满足下列条件:
-
每个分支结点最多有m棵子树(孩子结点)。
-
根结点不是叶子节点时至少有两棵子树,其他每个分支结点至少有[m/2]棵子树。
B+树绿色的节点称为叶子节点。蓝色节点(分支节点)又称为"索引"
-
结点的子树个数与关键字个数相等(B树节点两个分支,说明这个节点有三个关键字)
-
所有叶结点包含全部关键字及指向相应记录的指针,叶结点中将关键字按大小顺序排列,并且相邻叶结点按大小顺序相互链接起来。
-
分支节点只包括子节点关键字的最大值和指向子节点的指针。
3. B+树与B树对比
-
m阶B+树节点n个分叉对应n个关键字,m阶B树节点n个分叉对应n-1个关键字
-
m阶B树节点关键字个数范围[(m/2)-1,m-1](根节点[1,m-1])
m阶B+树节点关键字个数范围[m/2,m](根节点[1,m])
-
B+树中,叶节点包含全部关键字,非叶节点出现的关键字也会在叶子节点出现。
B树中,各个节点的关键字不会重复。
-
B+树中,叶结点包含信息,所有非叶结点仅起索引作用,非叶结点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针,不含有该关键字对应记录的存储地址。(查找元素需要一直找到叶节点)
B树的结点中都包含了关键字对应的记录的存储地址(如果中间节点找到了关键字元素,可以直接找到储存地址,无需到叶子节点上)
4. C++实现B树插入,中序遍历
#include <iostream>#include <vector>// order阶B树,节点最多order-1个元素,但是需要开辟order大小的空间,因为我是先插入后在判断扩容的
template <class ValueType, size_t order>
struct TreeNode
{std::vector<ValueType> _value; // 存放节点值std::vector<TreeNode<ValueType, order> *> _subs; // 存放节点的子树,空间大小为order+1TreeNode<ValueType, order> *_parent; // 父指针size_t _size; // 记录实际存储关键字个数TreeNode(){_value.resize(order);_subs.resize(order + 1);for (size_t i = 0; i < order; i++){_value[i] = ValueType();_subs[i] = nullptr;}_subs[order] = nullptr;_parent = nullptr;_size = 0;}
};template <class ValueType, size_t order>
class BTree
{typedef TreeNode<ValueType, order> TreeNode;private:TreeNode *_root = nullptr;public:BTree(const std::vector<ValueType> &vet){for (auto &val : vet){insert(val);}}BTree() = default;bool insert(const ValueType &value){if (_root == nullptr){_root = new TreeNode;_root->_value[0] = value;_root->_size += 1;return true;}else{// 找要插入的位置std::pair<TreeNode *, int> ret = _findPos(value);if (ret.second >= 0){// 不允许冗余return false;}TreeNode *cur = ret.first; // 要插入的节点int insert_value = value;TreeNode *child = nullptr;while (true){_insert(cur, insert_value, child);if (cur->_size == order){// 节点放满了需要分裂int mid = order / 2;TreeNode *node = new TreeNode; // node存放[mid+1,order-1]的数据size_t pos = 0;for (size_t i = mid + 1; i < order; i++){node->_value[pos] = cur->_value[i];node->_subs[pos] = cur->_subs[i];// 更新父节点if (cur->_subs[i] != nullptr){cur->_subs[i]->_parent = node;}pos += 1;// 将cur移出的位置清空cur->_value[i] = ValueType();cur->_subs[i] = nullptr;}// node节点中,新插入的值的孩子节点指针没处理node->_subs[order] = cur->_subs[order];if (cur->_subs[order] != nullptr){// 更新父节点cur->_subs[order]->_parent = node;}cur->_subs[order] = nullptr;node->_size = pos;cur->_size -= pos + 1; // cur还提取了一个值作为这两个节点父亲,下面的代码会操作ValueType midValue = cur->_value[mid];cur->_value[mid] = ValueType();if (cur->_parent == nullptr){// 新创建父节点,这个节点是cur和node的父亲_root = new TreeNode;_root->_value[0] = midValue;_root->_subs[0] = cur;_root->_subs[1] = node;_root->_size = 1;cur->_parent = _root;node->_parent = _root;break;}// 转划为向cur->_parent这个位置插入midValue问题,可以通过while循环解决insert_value = midValue;child = node;cur = cur->_parent;}else{// 节点没有插满,插入结束return true;}}}return true;}// 删除指定元素void erase(const ValueType &value){std::pair<TreeNode *, int> ret = _findPos(value);if (ret.second == -1){// 没有找到删除的元素return;}else{TreeNode *del = ret.first;if (!_isLeave(del)){// 如果删除的节点不是终端节点,转化为终端节点后在删除TreeNode *prev = del->_subs[ret.second]; // 找直接前继节点(左子树的最右节点)while (prev->_subs[ret.second + 1] != nullptr){prev = prev->_subs[ret.second + 1];}// 交换节点,转化为删除终端节点ValueType delValue = del->_value[ret.second];del->_value[ret.second] = prev->_value[prev->_size - 1];prev->_value[prev->_size - 1] = delValue;erase(delValue);}else{// 是终端节点,找其兄弟节点/*** @brief 考研对B树的代码不怎么考核,而删除的代码比较复杂,需要找这要删除这个节点的兄弟节点* 出于时间考虑,这里先空开。* 我认为删除节点操作需要找到删除节点的B树节点指针才行,这样才能准确的找到删除节点的兄弟B树节点的位置*/}}}void disPlayInorder(){_disPlay(_root);}private:bool _isLeave(TreeNode *node){bool ret = true;for (int i = 0; i < node->_size; i++){if (node->_subs[i] != nullptr){ret = false;break;}}return ret && node->_subs[node->_size] == nullptr;}void _disPlay(TreeNode *node){if (node == nullptr)return;for (size_t i = 0; i < node->_size; i++){_disPlay(node->_subs[i]);std::cout << node->_value[i] << " ";}// 最后剩余右子树_disPlay(node->_subs[node->_size]);}void _insert(TreeNode *node, int value, TreeNode *child){// 在数组中找value插入的位置,需要移动数组int endPos = node->_size - 1;while (endPos >= 0){if (value < node->_value[endPos]){// 挪动数据node->_value[endPos + 1] = node->_value[endPos];node->_subs[endPos + 2] = node->_subs[endPos + 1];endPos -= 1;}else{break;}}// endPos位置是第一个值小于value的位置,value要插入到其后边node->_value[endPos + 1] = value;node->_subs[endPos + 2] = child;if (child != nullptr){child->_parent = node;}node->_size += 1;}// 查找要插入的叶子节点以及数组下标std::pair<TreeNode *, int> _findPos(const ValueType &value){TreeNode *par = nullptr;TreeNode *cur = _root;while (cur != nullptr){int pos = 0; // 先从数组下标为0处开始while (pos < cur->_size){if (value < cur->_value[pos]){//_value[pos]左子树break;}else if (value > cur->_value[pos]){pos += 1;}else{return std::make_pair(cur, pos);}}par = cur;cur = cur->_subs[pos];}return std::make_pair(par, -1);}
};
#include "BTree.h"using namespace std;int main(int argc, char const *argv[])
{vector<int> ret = {2, 4, 1, 5, 7, 6, 0, 9, 3, 8};BTree<int, 5> tree(ret); // 5阶B树tree.disPlayInorder();// tree.erase(6);return 0;
}
代码仓库
相关文章:

数据结构-考研难点代码突破(C++实现树型查找 - B树插入与遍历,B+树基本概念)
数据结构(C)[B树(B-树)插入与中序遍历,效率分析]、B树、B*树、B树系列应用 文章目录1. B树B树的插入与删除流程2. B树(MySQL)3. B树与B树对比4. C实现B树插入,中序遍历1. B树 B树类…...
Python可视化界面编程入门
Python可视化界面编程入门具体实现代码如所示: (1)普通可视化界面编程代码入门: import sys from PyQt5.QtWidgets import QWidget,QApplication #导入两个类来进行程序界面编程if __name__"__main__":#创建一个Appl…...

基于Java+SpringBoot+Vue前后端分离书店购书系统设计与实现
博主介绍:✌全网粉丝3W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战✌ 博主作品:《微服务实战》专栏是本人的实战经验总结,《Spring家族及…...

Android:截屏/视频截图
需求描述 实现截取Android应用当前界面的功能,需包含界面中视频(此博客的参考代码以存储在设备本地的视频为例,未检验在线视频的情况)当前的播放帧截图。 调研准备 首先应用需要获取设备存储的读写权限,需要在Andro…...
leecode-C语言实现-28. 找出字符串中第一个匹配项的下标
一、题目给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。示例 1:输入:haystack …...

使用 Postman 实现 API 自动化测试
目录:导读 背景介绍 名词解析 使用说明 执行 API 测试 集成 CI 实现 API 自动化测试 写在最后 背景介绍 相信大部分开发人员和测试人员对 postman 都十分熟悉,对于开发人员和测试人员而言,使用 postman 来编写和保存测试用例会是一种比…...
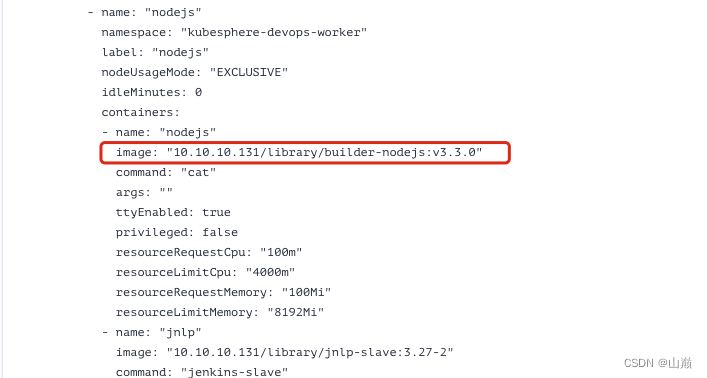
k8s环境jenkins发布vue项目指定nodejs版本
k8s环境jenkins发布vue项目指定nodejs版本1、背景2、分析3、解决方法3.1、 找到配置镜像位置3.2、 制作新镜像3.3、 推送镜像到私有仓库3.4、 修改配置文件1、背景 发布一个前端项目,它需要nodejs 16.9.0版本支持,而kubesphere 3.2.0集成的jenkins 的镜…...

我应该把毕业设计做到什么程度才能过关?
本篇博客包含了狗哥多年职业生涯对于软件项目的一丢丢理解,也讲述了对于大学生毕业设计的一些理解。如果你还是懵懵懂懂就要离开学校了,被老师告知不得不做出一套毕业设计的时候,希望你可以看到这篇博客,让你有点头绪,…...

力扣-合作过至少三次的演员和导演
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1050. 合作过至少三次的演员和导演二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运…...
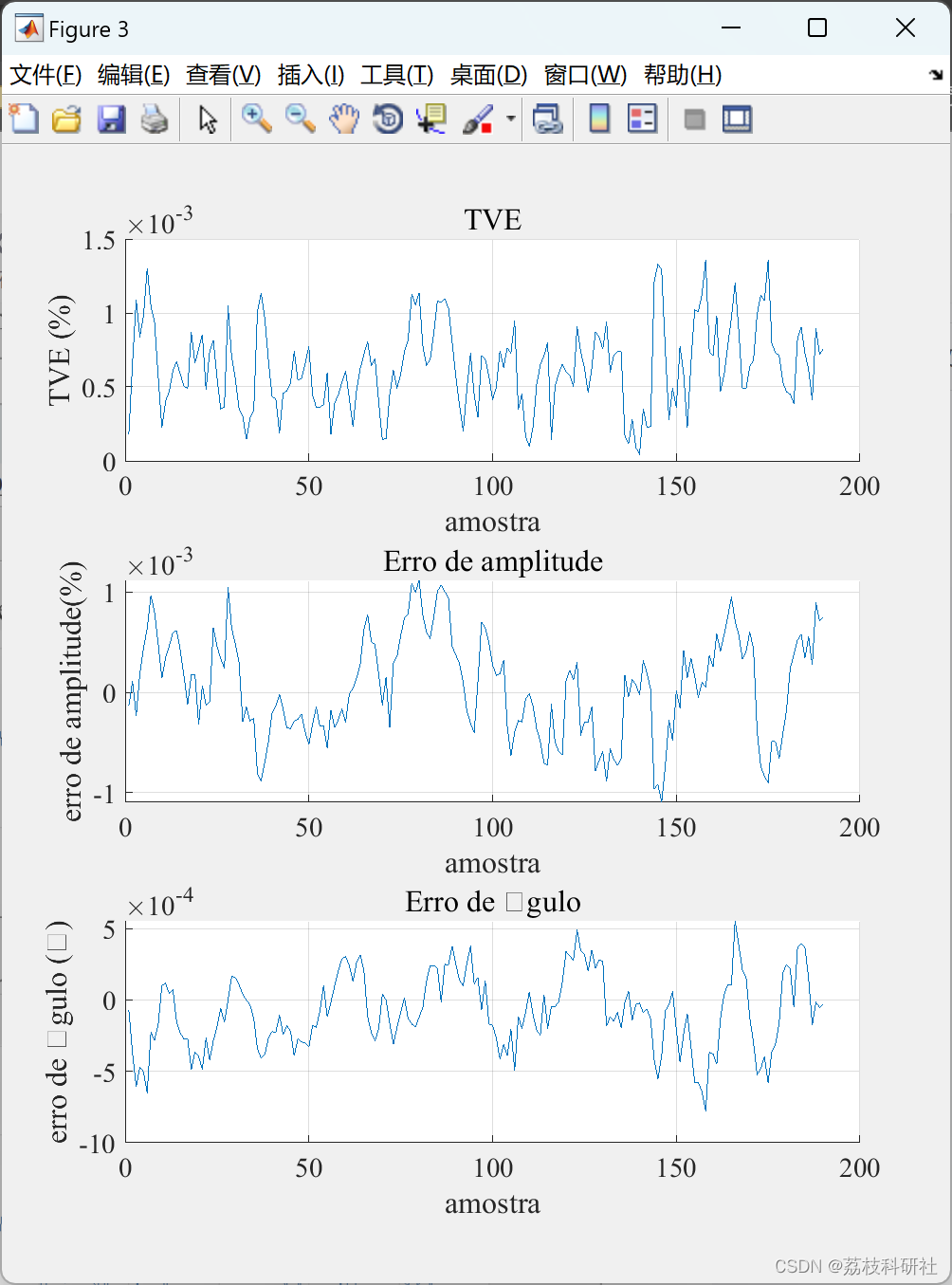
【 PMU】信号生成、采样、分割、估计器应用和误差计算(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...
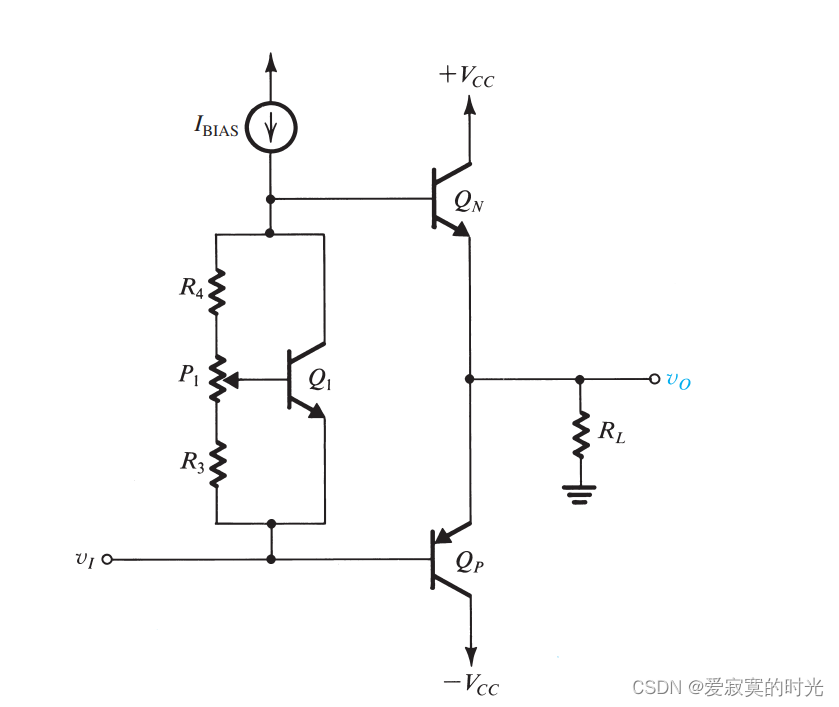
电子技术——AB类输出阶的偏置
电子技术——AB类输出阶的偏置 下面我们介绍两种AB类输出阶的偏置的方法。 使用二极管偏置 下图展示了电流源 III 加两个二极管的偏置方法: 因为输出阶需要大功率输出,因此输出推挽三极管可能是几何体积比较大的晶体管。对于二极管来说,并不…...
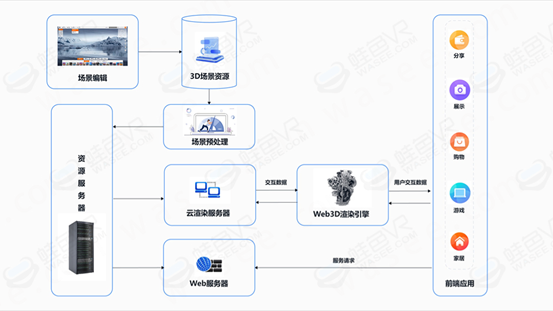
元宇宙营业厅,数字技术融合,赋能实体经济
在我国数字经济与虚拟服务市场规模扩大下,元宇宙营业厅强势来袭,从多场景、多内容,深耕高效协同的特色功能,基于多元化、灵活的交互体验,更大程度上解决线上业务办理抽象繁琐,线下业务办理的时空受限、业务…...

MySql面试精选—分库分表
目录 1、分库分表使用场景 2、常见的分库分表方案 3、常用的分库分表中间件...
Spring上下文生命周期
基于入口来分析 import org.springframework.context.annotation.AnnotationConfigApplicationContext; import org.springframework.context.annotation.ComponentScan; import org.springframework.context.annotation.Configuration;Configuration ComponentScan public cl…...

GitHub 标星 15w,如何用 Python 实现所有算法?
学会了 Python 基础知识,想进阶一下,那就来点算法吧!毕竟编程语言只是工具,结构算法才是灵魂。 新手如何入门 Python 算法? 几位印度小哥在 GitHub 上建了一个各种 Python 算法的新手入门大全。从原理到代码…...
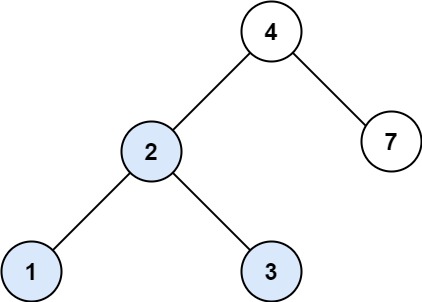
LeetCode 700. 二叉搜索树中的搜索
LeetCode 700. 二叉搜索树中的搜索 难度:easy\color{Green}{easy}easy 难度:middle\color{orange}{middle}middle 难度:hard\color{red}{hard}hard 题目描述 给定二叉搜索树(BST)的根节点 rootrootroot 和一个整数值…...
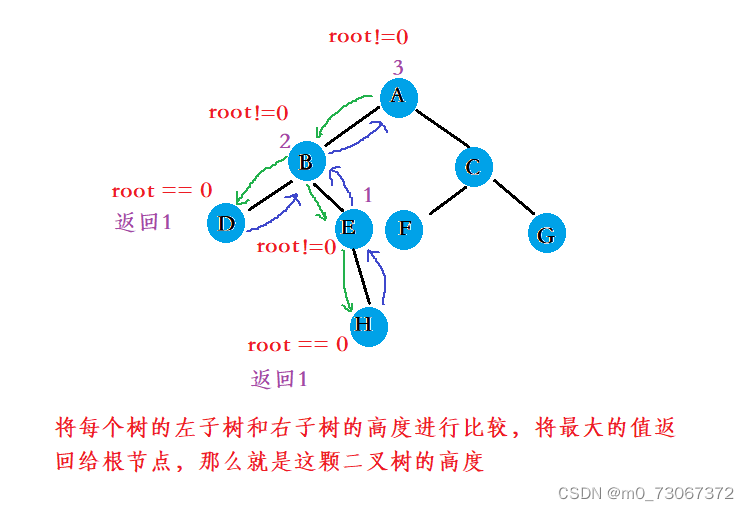
【数据结构】树与二叉树
目录 1、树的概念及结构 1.1、概念 1、树的特点 2、树与非树 1.2、概念 (重要) 1.3、树的表示形式 2、二叉树(重点) 2.1、概念 2.2、二叉树的特点 2.3、两种特殊的二叉树 1、满二叉树 2、完全二叉树 2.4、二叉树的性…...
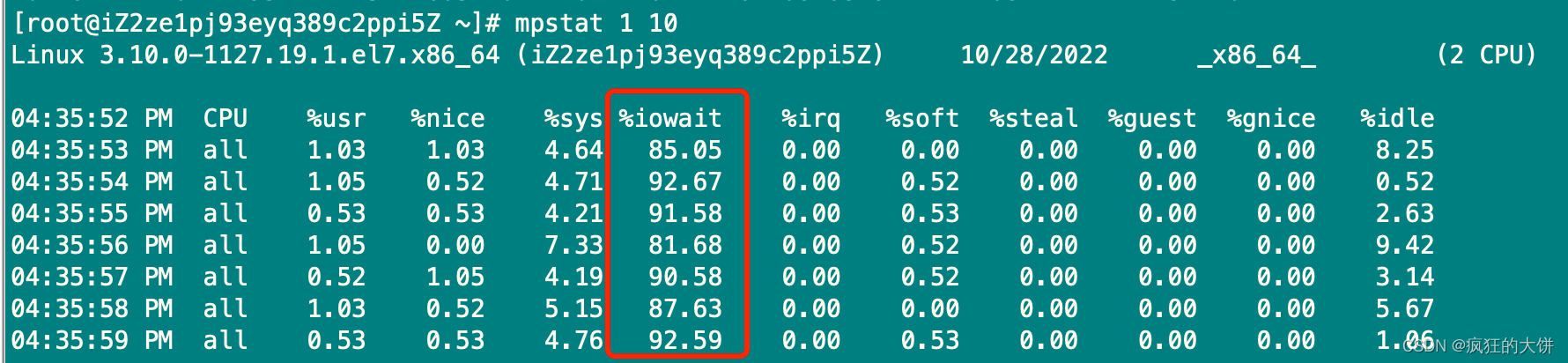
Stress压力工具的部署及使用
Stress压力工具的部署及使用 下载地址:wget https://fossies.org/linux/privat/old/stress-1.0.5.tar.gz 1.部署 进入目录执行./autogen.sh [rootiZ2ze1pj93eyq389c2ppi5Z stress-1.0.5]# ./autogen.sh ps:如果执行过程中缺包,安装对应的…...

[蓝桥杯 2020 省 AB3] 乘法表
题目描述九九乘法表是学习乘法时必须要掌握的。在不同进制数下,需要不同的乘法表。例如, 四进制下的乘法表如下所示:1*11 2*12 2*210 3*13 3*212 3*321请注意,乘法表中两个数相乘的顺序必须为样例中所示的顺序,不能随意交换两个乘…...

Python基础知识
基础知识 基础知识包括输入输出、变量、数据类型、表达式、运算符这5个方面。 1.输入输出 Python有很多函数,后面我们会细讲,但这里先将两个最基本的函数:输入和输出。 输出函数print(),在前面我们已经用过了,语法…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
