最优传输问题和Sinkhorn
最优传输问题
假设有M堆土,每堆土的大小是ama_mam,有N个坑,每个坑的大小是bnb_nbn,把单位土从土堆m运送到坑n的代价是c(m,n)c(m,n)c(m,n),如何找到一种运输方法填满坑,并且代价最小,这就是最优传输问题(optimal transport (OT) problem)。
假设有两个概率分布,类似上面的情况,如何以最小的成本将一种概率分布转换为另一种概率分布,这也是最优传输问题。这个最小的成本可以作为度量两个概率分布的距离,被称为Wasserstein距离,或者推土机距离(Earth Mover’s Distance(EMD))。
在离散的情况下,假设r,c\mathbf r, \mathbf cr,c是两个概率向量,也就是所有元素求和为1的向量。1d\mathbf 1_d1d是维度为ddd所有元素为1的向量。
运输多面体(transport polytope )U(r,c)U(\mathbf r,\mathbf c)U(r,c)被定义为:
U(r,c):={P∈R+d×d∣P1d=r,P⊤1d=c}U(\mathbf r,\mathbf c) := \{ \mathbf P \in \mathbb R^{d \times d}_+ | \mathbf P \mathbf 1_d = \mathbf r, \mathbf P^\top \mathbf 1_d = \mathbf c\} U(r,c):={P∈R+d×d∣P1d=r,P⊤1d=c}
给定一个费用矩阵M∈Rd×d\mathbf M \in \mathbb R^{d \times d}M∈Rd×d,r\mathbf rr到c\mathbf cc的最优传输距离被定义为:
dM(r,c):=minP∈U(r,c)<P,M>=∑i=1d∑j=1dPijMijd_{\mathbf M}(\mathbf r, \mathbf c) := \min_{\mathbf P \in U(\mathbf r,\mathbf c)}<\mathbf P, \mathbf M> = \sum_{i=1}^d \sum_{j=1}^d \mathbf{P}_{ij} \mathbf{M}_{ij} dM(r,c):=P∈U(r,c)min<P,M>=i=1∑dj=1∑dPijMij对于一般的矩阵M\mathbf MM,目前提出的最佳算法在最坏情况下的复杂度是 O(d3logd)O(d^3 \log d)O(d3logd)。在实践中复杂度也被证明是超立方的。
Sinkhorn距离
为上面的最优传输问题加上熵正则化:
dMλ(r,c)=minP∈U(r,c)∑i,jPijMij−1λh(P)h(P)=−∑i,jPijlogPijd_\mathbf{M}^\lambda(\mathbf{r}, \mathbf{c}) = \min_{\mathbf P\in U(\mathbf{r}, \mathbf{c})}\, \sum_{i,j} \mathbf P_{ij} \mathbf M_{ij} - \frac{1}{\lambda}h(\mathbf P)\\ h(\mathbf P) = -\sum_{i,j}\mathbf P_{ij}\log \mathbf P_{ij} dMλ(r,c)=P∈U(r,c)mini,j∑PijMij−λ1h(P)h(P)=−i,j∑PijlogPij dMλ(r,c)d_\mathbf{M}^\lambda(\mathbf{r}, \mathbf{c})dMλ(r,c)被称为dual-Sinkhorn divergence,h(P)h(\mathbf P)h(P)是香浓熵(Shannon entropy)。
当λ→0\lambda\rightarrow0λ→0时,上面问题的解是Pij=ricj\mathbf P_{ij}=\mathbf r_i \mathbf c_jPij=ricj;当λ→∞\lambda\rightarrow\inftyλ→∞时,回到了原始的最优输运问题。
香浓熵要求分配更加均匀, 参数λ\lambdaλ权衡了按花费分配和平分。
加上熵正则的最优传输问题变得更好计算了,因为解变得平滑。
Sinkhorn定理被用来寻找熵正则化最优输运问题的解。
参考资料
Wiki Sinkhorn’s theorem
Notes on Optimal Transport
http://alexhwilliams.info/itsneuronalblog/2020/10/09/optimal-transport/
https://zipjiang.github.io/2020/11/23/sinkhorn’s-theorem-,-sinkhorn-algorithm-and-applications.html
相关文章:

最优传输问题和Sinkhorn
最优传输问题 假设有M堆土,每堆土的大小是ama_mam,有N个坑,每个坑的大小是bnb_nbn,把单位土从土堆m运送到坑n的代价是c(m,n)c(m,n)c(m,n),如何找到一种运输方法填满坑,并且代价最小,这就是…...

Netty核心组件EventLoop源码解析
源码解析目标 分析最核心组件EventLoop在Netty运行过程中所参与的事情,以及具体实现 源码解析 依然用netty包example下Echo目录下的案例代码,单我们写一个NettyServer时候,第一句话就是 EventLoopGroup bossGroup new NioEventLoopGroup(…...

排障命令-汇总
目录 日志查询 1. grep 2. zgrep cpu 1. top 内存 1. free tcp相关 1. netstat 2. ulimit 3. lsof jvm常用 1. jps 2. jinfo 3. jstack 4. jmap 5. jstat 进制转换 1. 十进制转16进制 日志查询 1. grep 定义:(global regular expression) 命令用于查…...

python+pytest接口自动化(4)-requests发送get请求
python中用于请求http接口的有自带的urllib和第三方库requests,但 urllib 写法稍微有点繁琐,所以在进行接口自动化测试过程中,一般使用更为简洁且功能强大的 requests 库。下面我们使用 requests 库发送get请求。requests库简介requests 库中…...

开源电子书工具Calibre 6.3 发布
Calibre 开源项目是 Calibre 官方出的电子书管理工具。它可以查看,转换,编辑和分类所有主流格式的电子书。Calibre 是个跨平台软件,可以在 Linux、Windows 和 macOS 上运行。Calibre 6.3 正式发布,此次更新内容如下:新…...

C++ STL:适配器 Adapter
文章目录1、容器适配器1.1、stack1.2、queue1.3、priority_queue2、迭代器适配器2.1、插入迭代器2.2、反向迭代器2.3、流迭代器3、函数适配器3.1、* bindbind 使用方法bind 简化原理3.2、mem_fn适配器就是接口,对容器、迭代器、算法进行包装,但其实质还是…...

防抖和节流
防抖和节流的区别?防抖:触发高频事件后n 秒内 函数只会执行一次,如果n秒内 高频事件在在次触发,则会重新计算节流:高频事件触发,但在n 秒内 只会执行一次,所以节流会稀释函数的执行频率下面就是…...

vue3 微信扫码登录及获取个人信息实现的三种方法
一、流程: 微信提供的扫码方式有两种,分别是: 跳转二维码扫描页面 内嵌式二维码根据文档我们可以知道关于扫码授权的模式整体流程为: 1. 第三方发起微信授权登录请求,微信用户允许授权第三方应用后,微信会拉起应用或重定向到第三方网站&…...

Java8 新特性强大的Stream API
一、Stream API 说明 Java8中有两大最为重要的改变。第一个是 Lambda 表达式;另外一个则是 Stream API。 Stream API ( java.util.stream) 把真正的函数式编程风格引入到Java中。这是目前为止对Java类库最好的补充,因为Stream API可以极大提供Ja…...
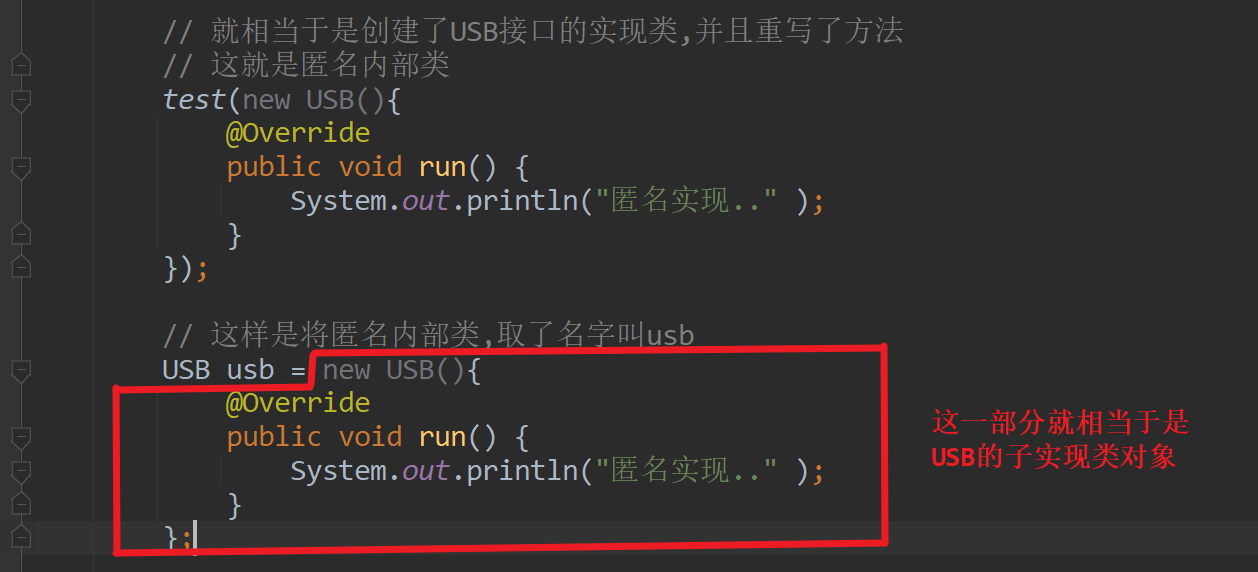
day22_IO
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、作业 二、缓冲流 三、字符流 四、缓冲字符流 五、匿名内部类 零、 复习昨日 File: 通过路径代表一个文件或目录 方法: 创建型,查找类,判断类,其他 IO …...
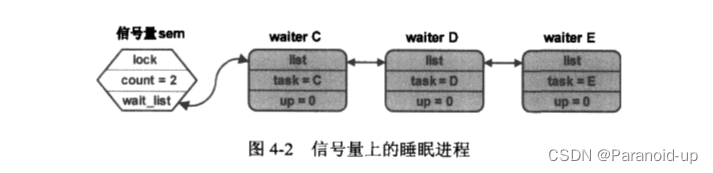
第三十八章 linux-并发解决方法二(信号量)
第三十八章 linux-并发解决方法二(信号量) 文章目录第三十八章 linux-并发解决方法二(信号量)信号量的定义DOWN操作UP操作相对于自旋锁,信号量的最大特点是允许调用它的线程进入睡眠状态这意味着试图获得某一信号的进程…...
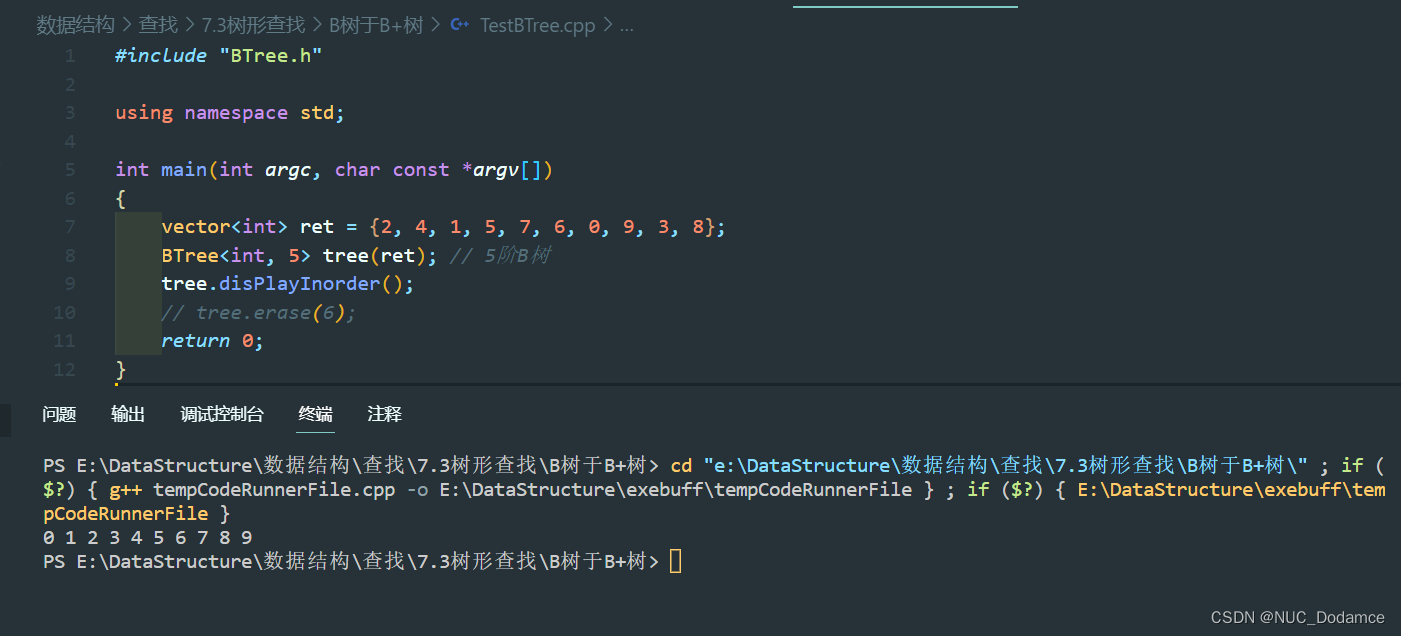
数据结构-考研难点代码突破(C++实现树型查找 - B树插入与遍历,B+树基本概念)
数据结构(C)[B树(B-树)插入与中序遍历,效率分析]、B树、B*树、B树系列应用 文章目录1. B树B树的插入与删除流程2. B树(MySQL)3. B树与B树对比4. C实现B树插入,中序遍历1. B树 B树类…...
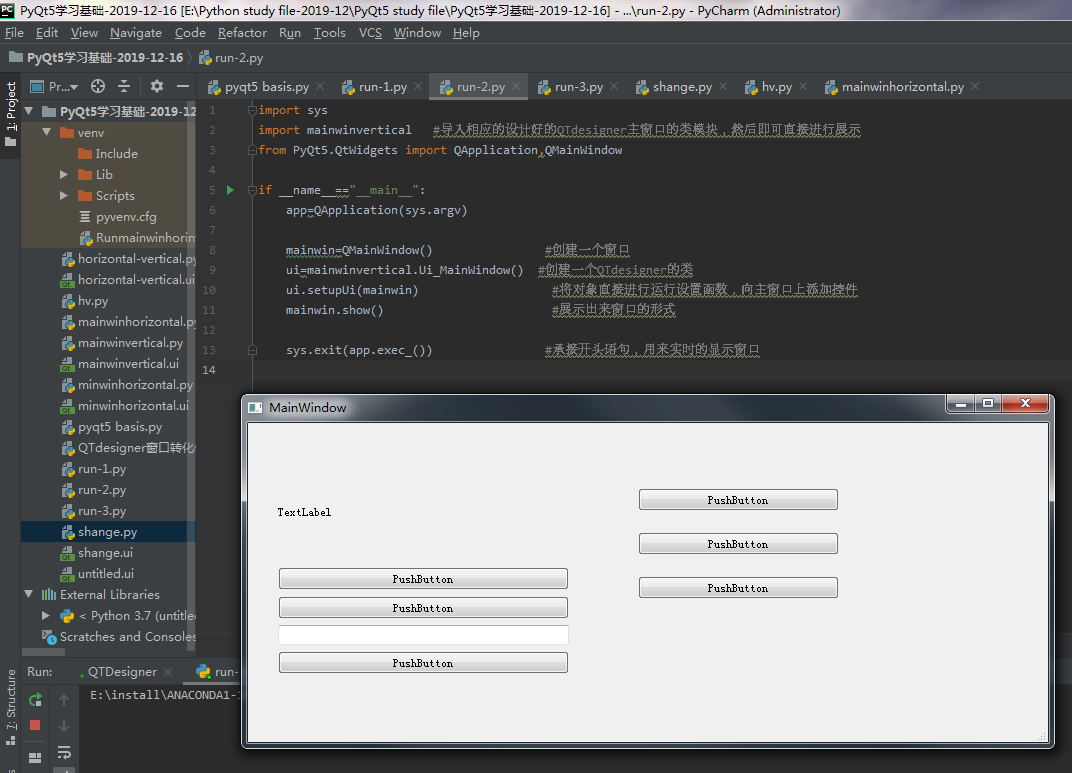
Python可视化界面编程入门
Python可视化界面编程入门具体实现代码如所示: (1)普通可视化界面编程代码入门: import sys from PyQt5.QtWidgets import QWidget,QApplication #导入两个类来进行程序界面编程if __name__"__main__":#创建一个Appl…...

基于Java+SpringBoot+Vue前后端分离书店购书系统设计与实现
博主介绍:✌全网粉丝3W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战✌ 博主作品:《微服务实战》专栏是本人的实战经验总结,《Spring家族及…...

Android:截屏/视频截图
需求描述 实现截取Android应用当前界面的功能,需包含界面中视频(此博客的参考代码以存储在设备本地的视频为例,未检验在线视频的情况)当前的播放帧截图。 调研准备 首先应用需要获取设备存储的读写权限,需要在Andro…...
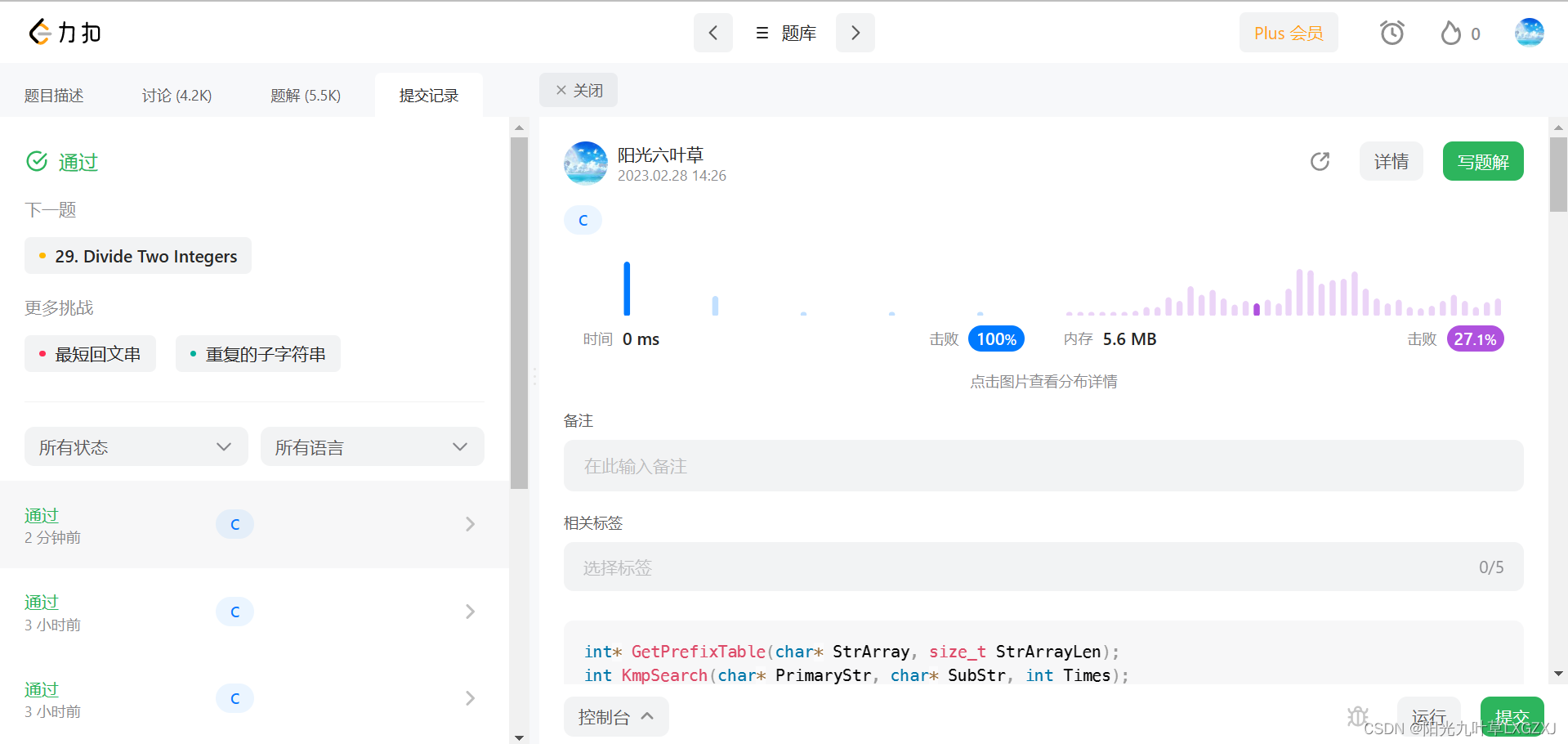
leecode-C语言实现-28. 找出字符串中第一个匹配项的下标
一、题目给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。示例 1:输入:haystack …...

使用 Postman 实现 API 自动化测试
目录:导读 背景介绍 名词解析 使用说明 执行 API 测试 集成 CI 实现 API 自动化测试 写在最后 背景介绍 相信大部分开发人员和测试人员对 postman 都十分熟悉,对于开发人员和测试人员而言,使用 postman 来编写和保存测试用例会是一种比…...
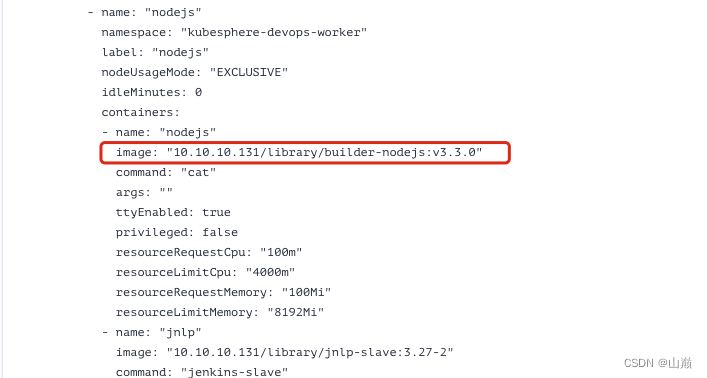
k8s环境jenkins发布vue项目指定nodejs版本
k8s环境jenkins发布vue项目指定nodejs版本1、背景2、分析3、解决方法3.1、 找到配置镜像位置3.2、 制作新镜像3.3、 推送镜像到私有仓库3.4、 修改配置文件1、背景 发布一个前端项目,它需要nodejs 16.9.0版本支持,而kubesphere 3.2.0集成的jenkins 的镜…...

我应该把毕业设计做到什么程度才能过关?
本篇博客包含了狗哥多年职业生涯对于软件项目的一丢丢理解,也讲述了对于大学生毕业设计的一些理解。如果你还是懵懵懂懂就要离开学校了,被老师告知不得不做出一套毕业设计的时候,希望你可以看到这篇博客,让你有点头绪,…...

力扣-合作过至少三次的演员和导演
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1050. 合作过至少三次的演员和导演二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
