算法训练营 day58 动态规划 判断子序列 不同的子序列
算法训练营 day58 动态规划 判断子序列 不同的子序列
判断子序列
392. 判断子序列 - 力扣(LeetCode)
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:
如果有大量输入的 S,称作 S1, S2, … , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
-
确定dp数组(dp table)以及下标的含义
dp[i][j]表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。注意这里是判断s是否为t的子序列。即t的长度是大于等于s的。
-
确定递推公式
在确定递推公式的时候,首先要考虑如下两种操作,整理如下:
-
if (s[i - 1] == t[j - 1])- t中找到了一个字符在s中也出现了
-
if (s[i - 1] != t[j - 1])- 相当于t要删除元素,继续匹配
if (s[i - 1] == t[j - 1]),那么dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符,相同子序列长度自然要在dp[i-1][j-1]的基础上加1(如果不理解,在回看一下dp[i][j]的定义)if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前元素t[j - 1]删除,那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了,即:dp[i][j] = dp[i][j - 1];
-
dp数组如何初始化
从递推公式可以看出
dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],所以dp[0][0]和dp[i][0]是一定要初始化的。这里大家已经可以发现,在定义
dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:

如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t,初始化就比较麻烦了。
dp[i][0] 表示以下标i-1为结尾的字符串,与空字符串的相同子序列长度,所以为0. dp[0][j]同理。
- 确定遍历顺序
同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],那么遍历顺序也应该是从上到下,从左到右
如图所示:

- 举例推导dp数组
以示例一为例,输入:s = “abc”, t = “ahbgdc”,dp状态转移图如下:

dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度,所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明:s与t的最长相同子序列就是s,那么s 就是 t 的子序列。
图中dp[s.size()][t.size()] = 3, 而s.size() 也为3。所以s是t 的子序列,返回true。
class Solution {public boolean isSubsequence(String s, String t) {int[][] dp = new int[s.length()+1][t.length()+1];char[] number1 = s.toCharArray();char[] number2 = t.toCharArray();for (int i = 1; i <= number1.length; i++) {for (int j = 1; j <=number2.length; j++) {if (number1[i-1]==number2[j-1]) dp[i][j] = dp[i-1][j-1]+1;else dp[i][j] = dp[i][j-1];System.out.print(dp[i][j]);}System.out.println();}return dp[number1.length][number2.length]==s.length();}
}
不同的子序列
115. 不同的子序列 - 力扣(LeetCode)
给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,“ACE” 是 “ABCDE” 的一个子序列,而 “AEC” 不是)
题目数据保证答案符合 32 位带符号整数范围。
- 确定dp数组(dp table)以及下标的含义
·dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
-
确定递推公式
这一类问题,基本是要分析两种情况
-
s[i - 1] 与 t[j - 1]相等 -
s[i - 1] 与 t[j - 1]不相等当
s[i - 1] 与 t[j - 1]相等时,dp[i][j]可以有两部分组成。一部分是用s[i - 1]来匹配,那么个数为
dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母,所以只需要dp[i-1][j-1]。一部分是不用
s[i - 1]来匹配,个数为dp[i - 1][j]。当
s[i - 1]与t[j - 1]相等时,dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];当
s[i - 1]与t[j - 1]不相等时,dp[i][j]只有一部分组成,不用s[i - 1]来匹配(就是模拟在s中删除这个元素),即:dp[i - 1][j]所以递推公式为:
dp[i][j] = dp[i - 1][j];
-
dp数组如何初始化
从递推公式
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]是从上方和左上方推导而来,如图:,那么dp[i][0]和dp[0][j]是一定要初始化的。

每次当初始化的时候,都要回顾一下dp[i][j]的定义,不要凭感觉初始化。
dp[i][0]表示什么呢?
dp[i][0] 表示:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。
那么dp[i][0]一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数就是1。
再来看dp[0][j],dp[0][j]:空字符串s可以随便删除元素,出现以j-1为结尾的字符串t的个数。
那么dp[0][j]一定都是0,s如论如何也变成不了t。
- 确定遍历顺序
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。

所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
- 举例推导dp数组
以s:“baegg”,t:"bag"为例,推导dp数组状态如下:

如果写出来的代码怎么改都通过不了,不妨把dp数组打印出来,看一看,是不是这样的。
class Solution {public int numDistinct(String s, String t) {char[] number1 = s.toCharArray();char[] number2 = t.toCharArray();int[][] dp = new int[number1.length+1][number2.length+1];for (int i = 0; i <=number1.length; i++) {dp[i][0]=1;}for (int i = 1; i <=number1.length ; i++) {for (int j = 1; j <=number2.length ; j++) {if (number1[i-1]==number2[j-1]) dp[i][j]=dp[i-1][j-1]+dp[i-1][j];else dp[i][j] = dp[i-1][j];}}return dp[number1.length][number2.length];}
}相关文章:

算法训练营 day58 动态规划 判断子序列 不同的子序列
算法训练营 day58 动态规划 判断子序列 不同的子序列 判断子序列 392. 判断子序列 - 力扣(LeetCode) 给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而…...

优思学院|DFMEA是全球制造业的必修课!
DFMEA(Design Failure Mode and Effects Analysis)是一种分析技术,在产品设计的早期阶段识别和解决潜在的失效问题。它通过分析设计的各个方面,识别潜在的失效模式和影响,并提出相应的改进措施,以减少失效的…...

【Day02数据结构 空间复杂度】
最近太忙了都好久没有更新博客了,太难了,抽空水一篇文章,大佬们多多支持. 上篇:时间复杂度分析 目录 前言 一、空间复杂度概念? 二、实例展示 三、.有复杂度要求的算法题练习 1.题目链接:力扣--消失的数字 2.题目链接:力扣--旋转数组 总结: 1…...

多数据库管理工具哪家强?ChatGPT点评,第一位并不是Navicat
SQL逐渐成为职场必备的编程语言,相信大家都不陌生。SQL是一种结构化查询语言,是用于数据库之间通信的编程语言。每个数据库都有着自己独特的访问规则,但大体上是遵循SQL标准。 因此,辗转于不同的数据库之间,开发者或D…...
)
UnityShader常用函数(UnityShader内置函数、CG和GLSL内置函数等)
空间变换函数函数名描述float4 UnityWorldToClipPos(float3 pos )把世界坐标空间中某一点pos变换到齐次裁剪空间float4 UnityViewToClipPos(float3 pos )把观察坐标空间中某一点pos变换到齐次裁剪空间float3 UnityObjectToViewPos(float3 pos或float4 pos)模型局部空间坐标系中…...

Springboot自定义注解-1
注解用于修饰其他的注解(纪委:管干部的干部) ① Retention:定义注解的保留策略 Retention(RetentionPolicy.SOURCE) //注解仅存在于源码中,在class字节码文件中不包含 Retention(RetentionPolicy.CLASS) …...
)
经纬度标定及大地坐标系相关概念(一)
经纬度标定及大地坐标系相关概念(一)一、背景二、经纬度的概念三、大地坐标系四、大地坐标系的分类五、各类坐标系介绍5.1 我国地理坐标系5.1.1 北京54坐标系5.1.2 1980西安坐标系5.1.3 2000国家大地坐标系5.2 世界大地坐标系5.1.1 WGS84坐标系5.3 加密坐…...
synchronized关键字原理
synchronized原理 1、基本特点 基于锁策略,可以知道synchronized具有以下特性: 1.开始时候是乐观锁,如果锁冲突频繁就转换为悲观锁 2.开始是轻量级锁,如果锁持有的时间较长,就转换成重量级锁 3.实现轻量级锁的时候…...

面试被问死怎么办?学会这四招,通过的机率提升30%
软件工程师面试很难,难到什么程度呢?有一句话可以来形容: 面试造飞机,上班拧螺丝 没错,面试的时候各种问你原理、机制,而这些在实际工作中却很难用到。于是乎,很多工程师面试的时候就非常害怕…...
Android TV UI开发常用知识
导入依赖 Google官方为Android TV的UI开发提供了一系列的规范组件,在leanback的依赖库中,这里介绍一些常用的组件,使用前需要导入leanback库。 implementation androidx.leanback:leanback:$version常用的页面 这些Fragment有设计好的样式&…...
Xshell 下载及安装
文章目录下载安装连接服务器Xshell 是一个强大的安全终端模拟软件,它支持SSH1, SSH2, 以及Microsoft Windows 平台的TELNET 协议。Xshell 通过互联网到远程主机的安全连接以及它创新性的设计和特色帮助用户在复杂的网络环境中享受他们的工作。 Xshell可以在Windows界…...
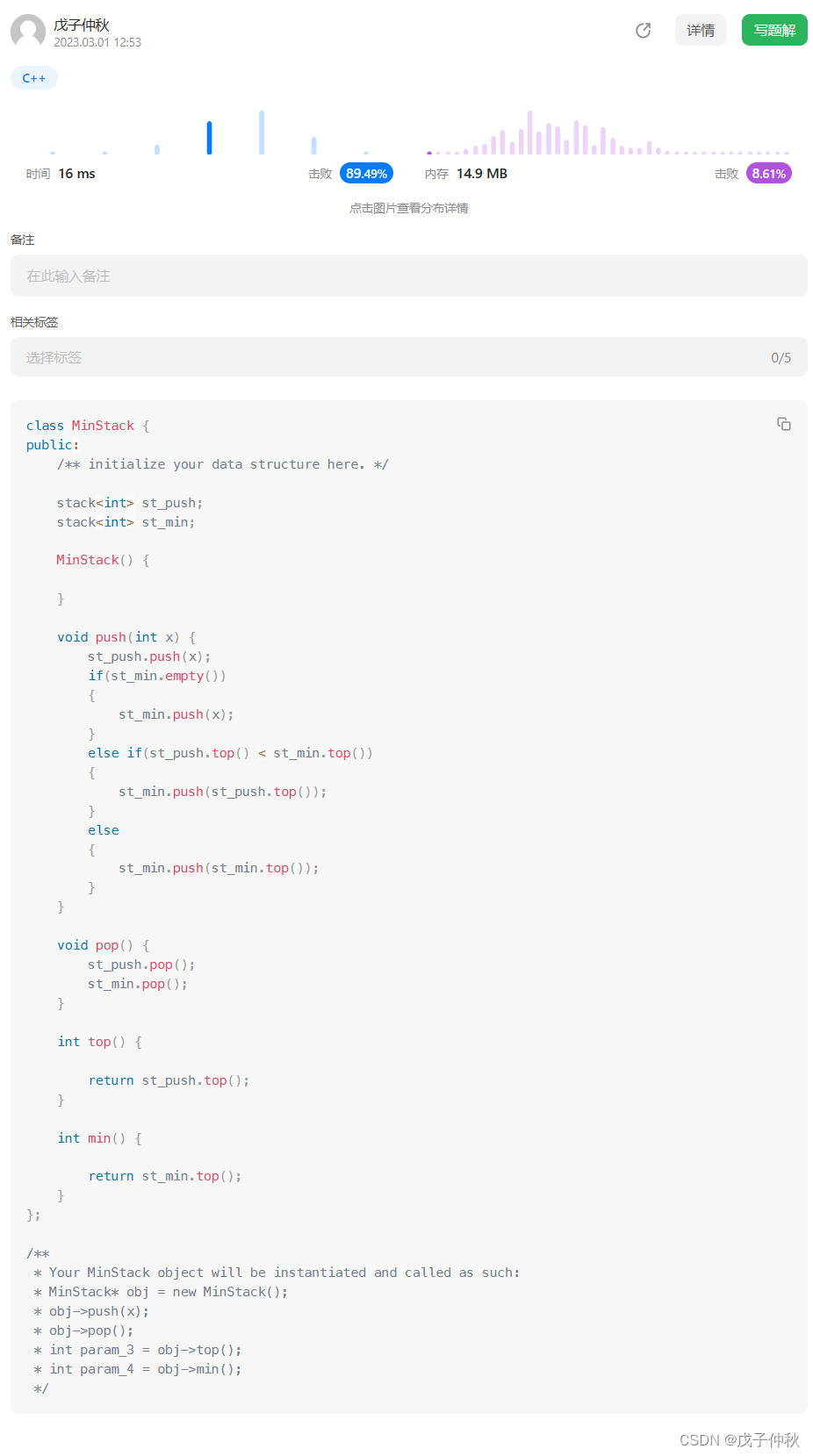
【LeetCode】剑指 Offer(12)
目录 题目:剑指 Offer 30. 包含min函数的栈 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer 30. 包含m…...

vue在history模式下打包部署问题解决
引言 项目使用的模板是element-template,由于业务需要,我将路由的hash模式更改为了history模式,然后在打包部署项目时就出现了问题 个人发现是资源的访问路径有问题,在部署之后发现每次访问的js资源路径前都会自动携带上我路由的…...

Java中常见性能优化策略的总结
文章目录1. 代码优化2. 数据库层面优化SQL调优架构层面的调优连接池调优3. 网络优化4. 缓存缓存分类使用场景选型考虑什么时候更新缓存?如何保障更新的可靠性和实时性?缓存是否会满,缓存满了怎么办?缓存是否允许丢失?丢…...

c++日志库log4cplus使用
项目中需要打印log,方便程序调试和问题定位分析。C实现的log4cplus日志库是一种易于使用的C 日志记录API,可提供线程安全,灵活且任意粒度的日志管理和配置控制。 下面介绍一下在linux中安装log4cplus库过程 下载地址:https://gi…...
什么是接口测试,我们如何实现接口测试?
1. 什么是接口测试 顾名思义,接口测试是对系统或组件之间的接口进行测试,主要是校验数据的交换,传递和控制管理过程,以及相互逻辑依赖关系。其中接口协议分为HTTP,WebService,Dubbo,Thrift,Socket等类型,测试类型又主…...
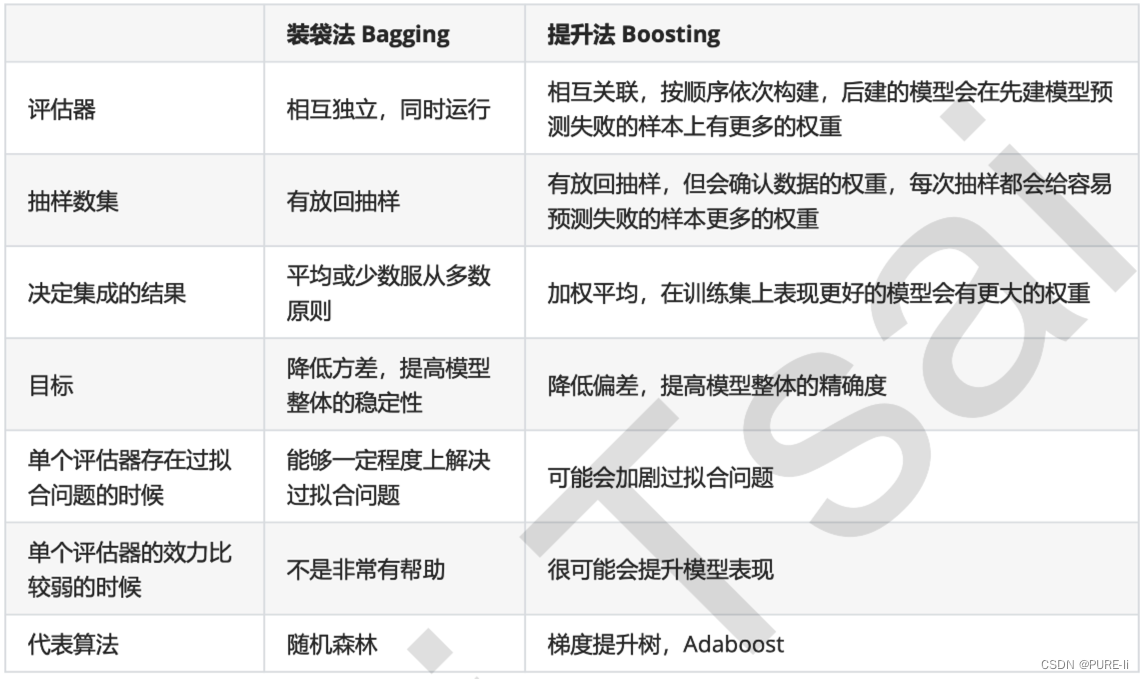
随机森林在sklearn中的实现
目录 一.集成算法 二.sklearn中的集成算法模块ensemble 三.RandomForestClassifier(随机森林分类器) 四.重要参数 1.基评估器参数 2.随机森林参数 五.重要属性和接口 六.Bagging的另一个必要条件 七.RandomForestRegressor(随机森林回归器) 八.机器学习中调参的基本思…...

[论文总结] 深度学习在农业领域应用论文笔记11
深度学习在农业上的应用笔记11 最近发表的相关论文数量不多,质量普遍也不尽如人意,尤其是《Computers and Electronics in Agriculture》这个期刊。这些论文的方法都很简单,只是强行将深度学习应用于某个问题上,而没有考虑到农业…...

Android 9.0 SystemUI 状态栏屏蔽弹出的悬浮式通知
1.概述 在9.0的系统ROM产品定制化开发中,在systemui的状态栏中,会在有闹钟 wifi连接等特殊弹窗通知的时候,会在接收到系统通知时,弹窗悬浮式弹窗通知,然后过几秒中, 就消失了,所以像这样的悬浮式通知,在有些产品中是不需要的,要求屏蔽掉,这就需要按照悬浮式流程来分析…...
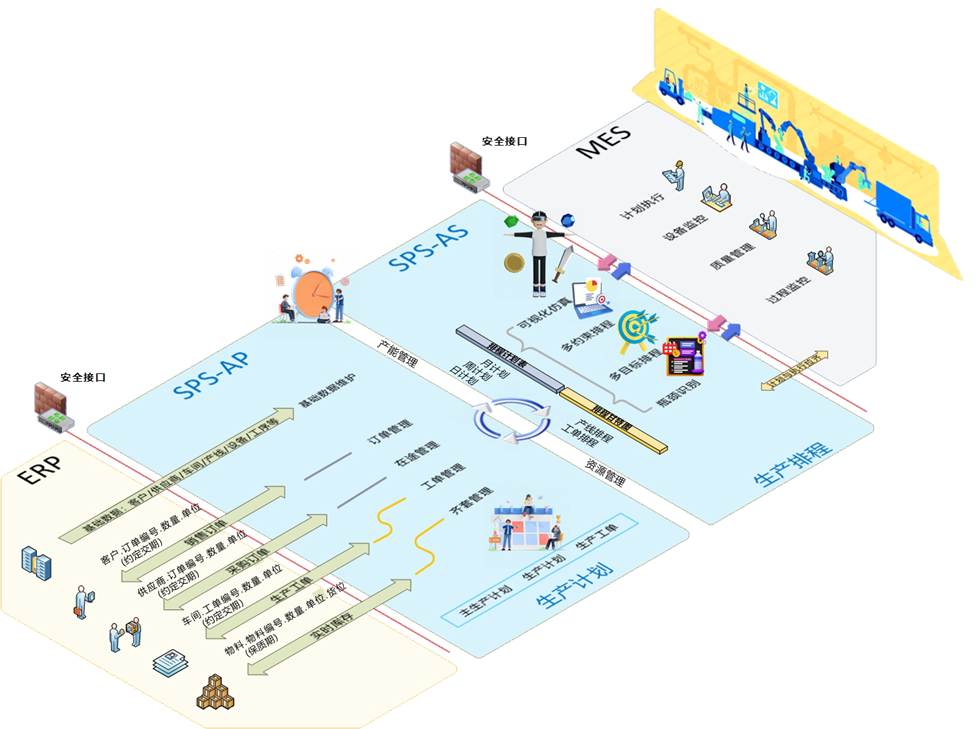
商简智能计划与排程SPS在纺织行业中的应用
企业背景 某织造、染色及后整理一体化工艺的纺织面料企业,主要从事户外功能运动服装、内衣、泳衣、汽车内饰等面料的研发和销售,年产值在20亿左右,是迪卡侬运动面料最优质供应商之一。 纺织行业特点 印染具有典型的流程行业特性,…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
