植物大战 二叉搜索树——C++
这里是目录标题
- 二叉排序树的概念
- 模拟二叉搜索树
- 定义节点类
- insert非递归
- Find
- erase(重点)
- 析构函数
- 拷贝构造(深拷贝)
- 赋值构造
- 递归
- FindR
- InsertR
- 二叉搜索树的应用
- k模型
- KV模型
二叉排序树的概念
单纯的二叉树存储数据没有太大的作用。
搜索二叉树作用很大。
搜索二叉树的一般都是用来查找。也可以用来排序,所以也叫做二叉排序树。
叫做二叉排序树的原因是因为他中序遍历是有序的。
因为中序的任何一颗子树,都要先走左子树,根,再走右子树。
搜索树因为数据不能冗余,所以也可以用来在插入的时候去重。
因为左子树<根<右子树,所以走中序出来,就是排序好的结果。
搜索二叉树要满足:
任意一颗子树都要满足,左子树的值小于根,右子树的值大于根。
优点:查找速度非常快。查找一个值,最多查找高度次,但是它的查找速度是O(n)。因为它有可能是单边树。所以后面会有一个平衡搜索二叉树,不如AVL树,红黑树。
但是我们要从搜索二叉树学起。
模拟二叉搜索树
搜索树的模板参数喜欢用k。k表示关键词的意思,因为喜欢搜索。
定义节点类
需要先定一个节点类。
template<class K>
struct BSTNode
{BSTNode<K>* _pLeft;BSTNode<K>* _pRight;K _key;
};
然后开始写二叉树的增删查改。
insert非递归
原则上插入不能有相同的数据插入。
搜索二叉树的插入顺序会影响效率。一般有序的话会影响。
为了能够找到cur的上一个结点,所以需要再定义个parent的节点。
template <class K>
class BSTree
{typedef BSTreeNode Node;//名字优化
public:bool Insert(const K& key){//如果根节点为空if (_root == nullptr){//new的时候直接可以填值。_root = new Node(key);return bool;}//否则开始Node* cur = _root;Node* parent = nullptr;while (cur){//如果在左边if (key > cur->_key){parent = cur;cur = cur->_right;}//如果在右边else if(key < cur->_key){parent = cur;cur = cur->_left;}//不允许数据冗余else{return false;}}//循环结束,new一个空间.cur = new Node(key);//不知道链接到父亲的左边和右边。//这时候就需要再比较一次if (key > parent->_key){parent->_right = cur;}else{parent->_left = cur;}return true;}
private:Node* _root = nullptr;//根节点
};
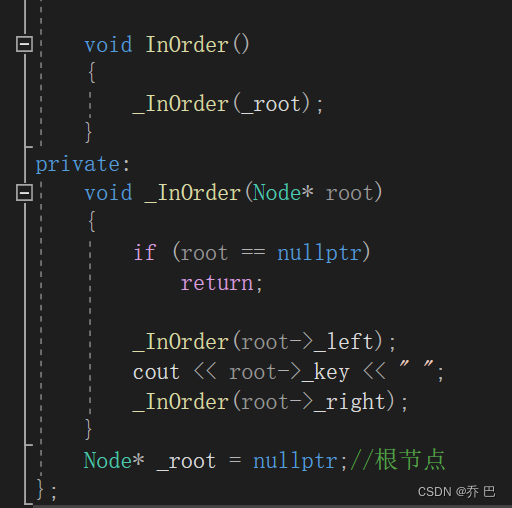
C++的根节点是私有的,封装了。所以没办法访问。
可以提供函数。也可以套一层。用_InOrder。
然后把_InOrder函数设为私有。
这样就不用传参了。
Find
查找值更简单。
bool Find(const K& key){Node* cur = _root;while(cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}
erase(重点)
搜索树前面的问题都不算问题,最大的问题在于删除数据。删除数据是一个非常麻烦的事情。
1.删叶子节点最好删。
2.删只有一个孩子的也挺好删。只有一个孩子的话,托付给父亲就行,和Linux的托孤有点相似。
总结:没有孩子或者只有一个孩子的时候可以直接删除。
3.不好删的是:
假如有两个孩子则不好删。
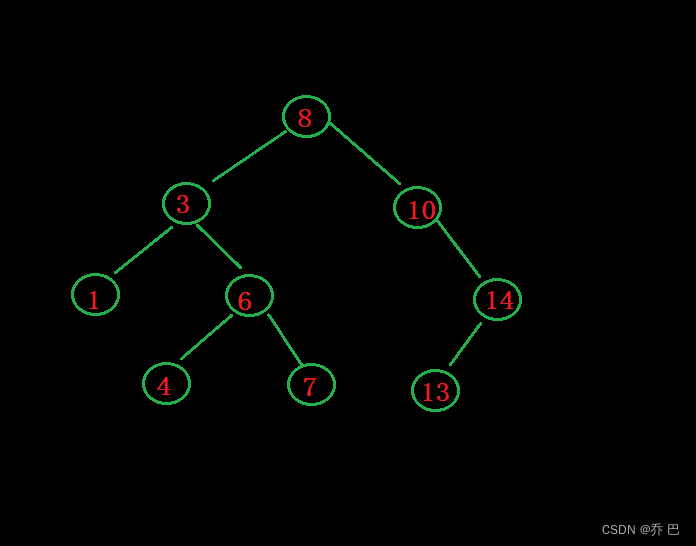
比如删除3。3有两个孩子。3的父亲8管不了两个孩子,因为8右子树也有孩子。
这时候需要用替换法删除。
替换法删除:
找谁替换呢?
找左子树的最大值结点。或者右子树的最小值结点。
为什么?
因为一棵搜索二叉树,最左边就是最小的值。最右边是最大的值。
关键理解:左子树的最大值结点做父亲可以满足比左子树的任意一个结点的值都大,同时随便拿出左子树的任意一个结点都比右子树小。
理解了上面的。有人找出了规律。
重点:
分三种情况
1.假如删除的节点的左子树为空(包括两个节点都为空的情况)。
2.假如删除的节点的右子树为空。(要注意假如是根节点的情况)
3.假如删除的节点的左右子树都不为空(替换法删除)。
具体遇到的bug需要根据实际图来解决。上面的三种情况只是个大概。
//非递归删除erasebool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while(cur){if(key > cur->_key){parent = cur;cur = cur->_right;}else if(key < cur->_key) {parent = cur;cur = cur->_left;}else{//一个孩子 假如 左为空if(cur->_left == nullptr){if(cur == _root){_root = cur->_right;}else{if(cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}//假如右为空else if(cur->_right == nullptr){if(cur == _root){_root = cur->_left;}else{if(cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}//两个孩子都不为空else{//右子树最小节点替代Node* minParent = cur;Node* minRight = cur->_right;while(minRight->_left){minParent = minRight;minRight = minRight->_left;}swap(minRight->_key, cur->_key);if(minParent->_left == minRight){minParent->_left = minRight->_right;}else{minParent->_right = minRight->_right;}delete minRight;}return true;}}return false;}
析构函数
因为没有参数,无法调用析构函数递归,所以需要套一层进行递归。
private:
void DestortTree(Node* root)
{if(root == nullptr)return;DestoryTree(root->_left);DestoryTree(root->_right);delete root;
}
public:
~BSTree()
{DestoryTree(_root);_root = nullptr;
}
拷贝构造(深拷贝)
注意:只要有了拷贝构造就不会再生成默认的构造函数了,所以为了写拷贝构造函数,需要先写一个构造函数。
这时候就要显式写一个构造函数。或者可以用C++11的关键字default来强制生成默认构造
BSTree() = default;
假如我们不写拷贝构造函数,会默认生成构造函数进行浅拷贝。
为了保证树的形状,只能用前序遍历(根 左子树 右子树)递归拷贝。
private:
Node* CopyTree(Node* root)
{if(root == nullptr)return nullptr;Node* copyNode = new Node(root->key);copyNode->_left = CopyTree(root->_left);copyNode->_right = CopyTree(root->_right);return copyNode;
}
public:
BSTree(const BSTree<K>& t)
{_root = CopyTree(t._root);
}
赋值构造
// t1 = t2
BSTree<K>& operator=(BSTree<K> t)
{swap(_root, t._root);return *this;
}
递归
FindR
返回下表的原因是因为要修改,但是这个树不需要修改,修改会破坏掉结构。所以返回bool值就ok。
C++类只要走递归一般都要套一层。不套一层一般都无法走递归。
InsertR
bool InsertR(const K& key){return _InsertR(_root, key);}bool _InsertR(Node*& root, const K& key){if(root == nullptr){root = new Node(key);return true;}if(root->_key < key)return _InsertR(root->_right, key);else if(root->_key > key)return _InsertR(root->_left, key);elsereturn false;}
二叉搜索树的应用
k模型
k模型只有key作为关键码,结构中只需要存储key杰克,关键码即为需要搜索到的值,比如给一个单词word,检查该单词是否拼写正确。
实质:就是判断K在不在这个系统中
K模型也可以用来去重+排序,
KV模型
KV模型的每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。
1、比如英汉词典中的英文和中文的对应关系,构成了<word,chinese> 的键值对
2、统计单词出现的次数,<word, count>的关系就是一个键值对。
再比如高铁刷身份证进站。
相关文章:

植物大战 二叉搜索树——C++
这里是目录标题二叉排序树的概念模拟二叉搜索树定义节点类insert非递归Finderase(重点)析构函数拷贝构造(深拷贝)赋值构造递归FindRInsertR二叉搜索树的应用k模型KV模型二叉排序树的概念 单纯的二叉树存储数据没有太大的作用。 搜索二叉树作用很大。 搜索二叉树的一般都是用…...

[MatLab]矩阵运算和程序结构
一、矩阵 1.定义 矩阵以[ ]包含,以空格表示数据分隔,以;表示换行。 A [1 2 3 4 5 6] B 1:2:9 %1-9中的数,中间是步长(不能缺省) C repmat(B,3,2) %将B横向重复2次,纵向重复2次 D ones(2,4) …...

【Leedcode】栈和队列必备的面试题(第四期)
【Leedcode】栈和队列必备的面试题(第四期) 文章目录【Leedcode】栈和队列必备的面试题(第四期)一、题目二、思路图解1.声明结构体2.循环链表开辟动态结构体空间3.向循环队列插入一个元素4.循环队列中删除一个元素5. 从队首获取元…...
Windows Server 2016搭建文件服务器
1:进入系统在服务器管理器仪表盘中添加角色和功能。 2:下一步。 3:继续下一步。 4:下一步。 5:勾选Web服务器(IIS) 6:添加功能。 7:下一步。 8:下一步。 9:下一步。 10&a…...
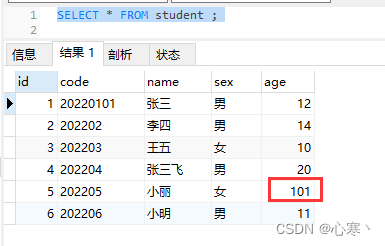
零基础学SQL(十一、视图)
目录 前置建表 一、什么是视图 二、为什么使用视图 三、视图的规则和限制 四、视图的增删改查 五、视图数据的更新 前置建表 CREATE TABLE student (id int NOT NULL AUTO_INCREMENT COMMENT 主键,code varchar(255) NOT NULL COMMENT 学号,name varchar(255) DEFAULT NUL…...
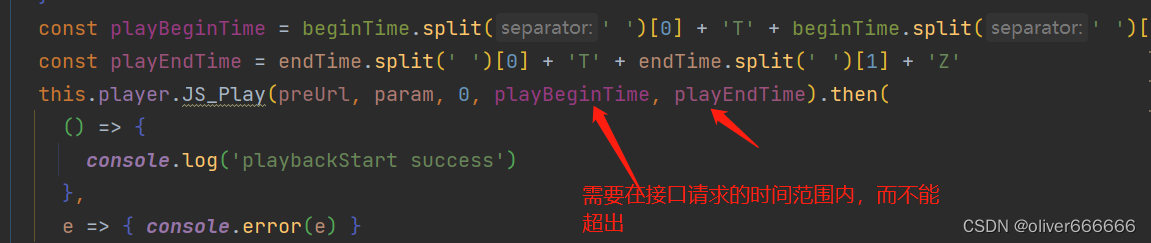
web,h5海康视频接入监控视频流记录三(后台node取流)
前端vue,接入ws视频播放 云台控制 ,回放预览,都是需要调对应的海康接口。相当于,点击时,请求后台写好的接口,接口再去请求海康的接口 调用云台控制是,操作一次,不会自己停止&#x…...

网络安全从入门到精通:30天速成教程到底有多狠?你能坚持下来么?
毫无疑问,网络安全是当下最具潜力的编程方向之一。对于许多未曾涉足计算机编程的领域「小白」来说,深入地掌握网络安全看似是一件十分困难的事。至于一个月能不能学会网络安全,这个要看个人,对于时间管理不是很高的,肯…...

世界上最流行的编程语言,用户数超过Python,Java,JavaScript,C的总和!
世界上最流行的编程语言是什么? Python? Java? JavaScript? C?都不是,是Excel!外媒估计,全球有12亿人使用微软的Office套件,其中估计有7.5亿人使用Excel!可是Excel不就是能写点儿公式&#x…...

杂谈:created中两次数据修改,会触发几次页面更新?
面试题:created生命周期中两次修改数据,会触发几次页面更新? 一、同步的 先举个简单的同步的例子: new Vue({el: "#app",template: <div><div>{{count}}</div></div>,data() {return {count…...

原生JS实现拖拽排序
拖拽(这两个字看了几遍已经不认识了) 说到拖拽,应用场景不可谓不多。无论是打开电脑还是手机,第一眼望去的界面都是可拖拽的,靠拖拽实现APP或者应用的重新布局,或者拖拽文件进行操作文件。 先看效果图&am…...

Coredump-N: corrupted double-linked list
文章目录 问题安装debuginfo之后分析参数确定确定代码逻辑解决问题 今天碰到一例: #0 0xf7f43129 in __kernel_vsyscall () #1 0xf6942b16 in raise () from /lib/libc.so.6 #2 0xf6928e64 in abort () from /lib/libc.so.6 #3 0xf6986e8c in __libc_message () from /lib/li…...

5个好用的视频素材网站
推荐五个高质量视频素材网站,免费、可商用,赶紧收藏起来! 1、菜鸟图库 视频素材下载_mp4视频大全 - 菜鸟图库 网站素材非常丰富,有平面、UI、电商、办公、视频、音频等相关素材,视频素材质量很高,全部都是…...

使用码匠连接一切|二
目录 Elasticsearch Oracle ClickHouse DynamoDB CouchDB 关于码匠 作为一款面向开发者的低代码平台,码匠提供了丰富的数据连接能力,能帮助用户快速、轻松地连接和集成多种数据源,包括关系型数据库、非关系型数据库、API 等。平台提供了…...

3.1.1 表的相关设计
文章目录1.表中实体与实体对应的关系2.实际案例分析3.表的实际创建4.总结1.表中实体与实体对应的关系 一对多 如一个班级对应多名学生,一个客户拥有多个订单等这种类型表的建表要遵循主外键关系原则,即在从表创建一个字段,此字段作为外键指向…...
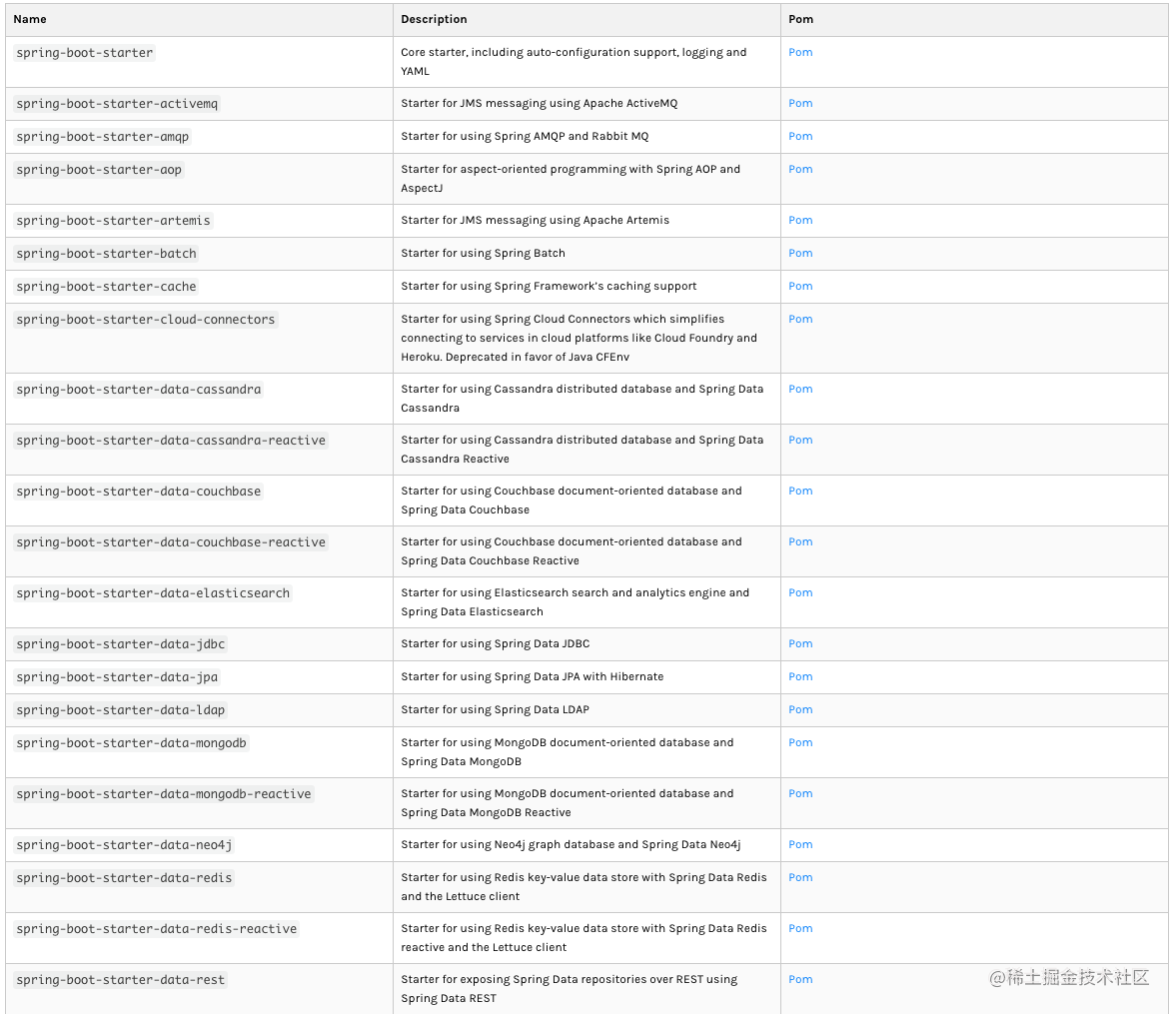
Vue3 企业级项目实战:认识 Spring Boot
Vue3 企业级项目实战 - 程序员十三 - 掘金小册Vue3 Element Plus Spring Boot 企业级项目开发,升职加薪,快人一步。。「Vue3 企业级项目实战」由程序员十三撰写,2744人购买https://s.juejin.cn/ds/S2RkR9F/ 越来越流行的 Spring Boot Spr…...
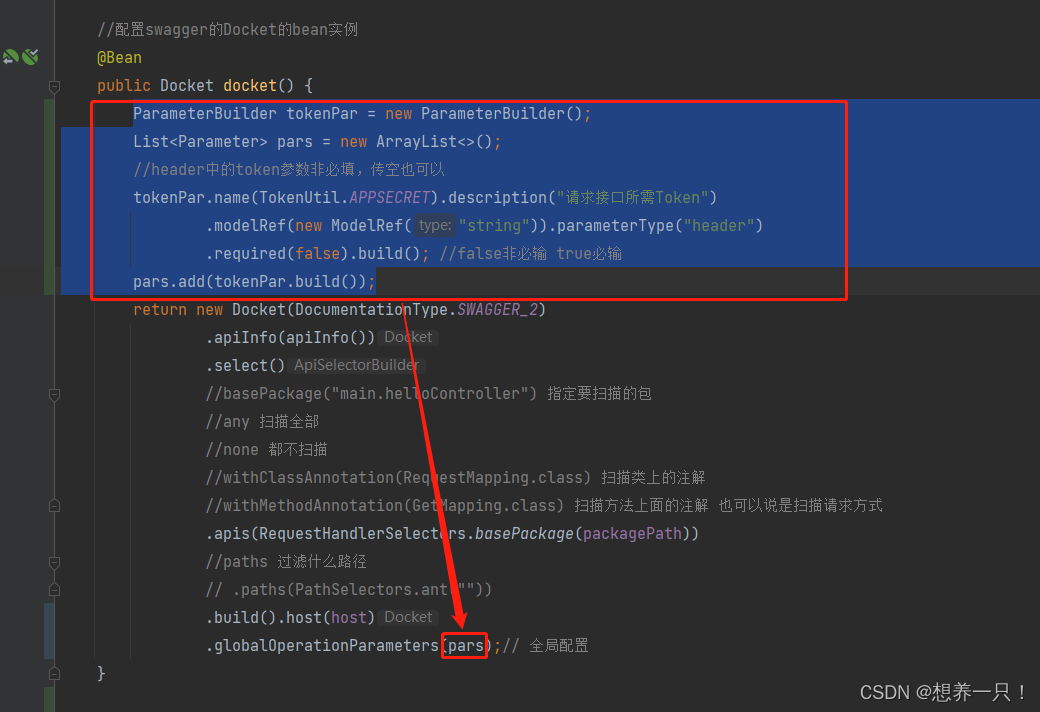
Swagger2实现配置Header请求头
效果 实现 大家使用swagger肯定知道在代码中会写一个 SwaggerConfig 配置类,如果没有这个类swagger指定也用不起来,所以在swagger中配置请求头也是在这个 SwaggerConfig 中操作。 1、要实现配置请求头在配置swagger的Docket的bean实例中添加一个 globa…...
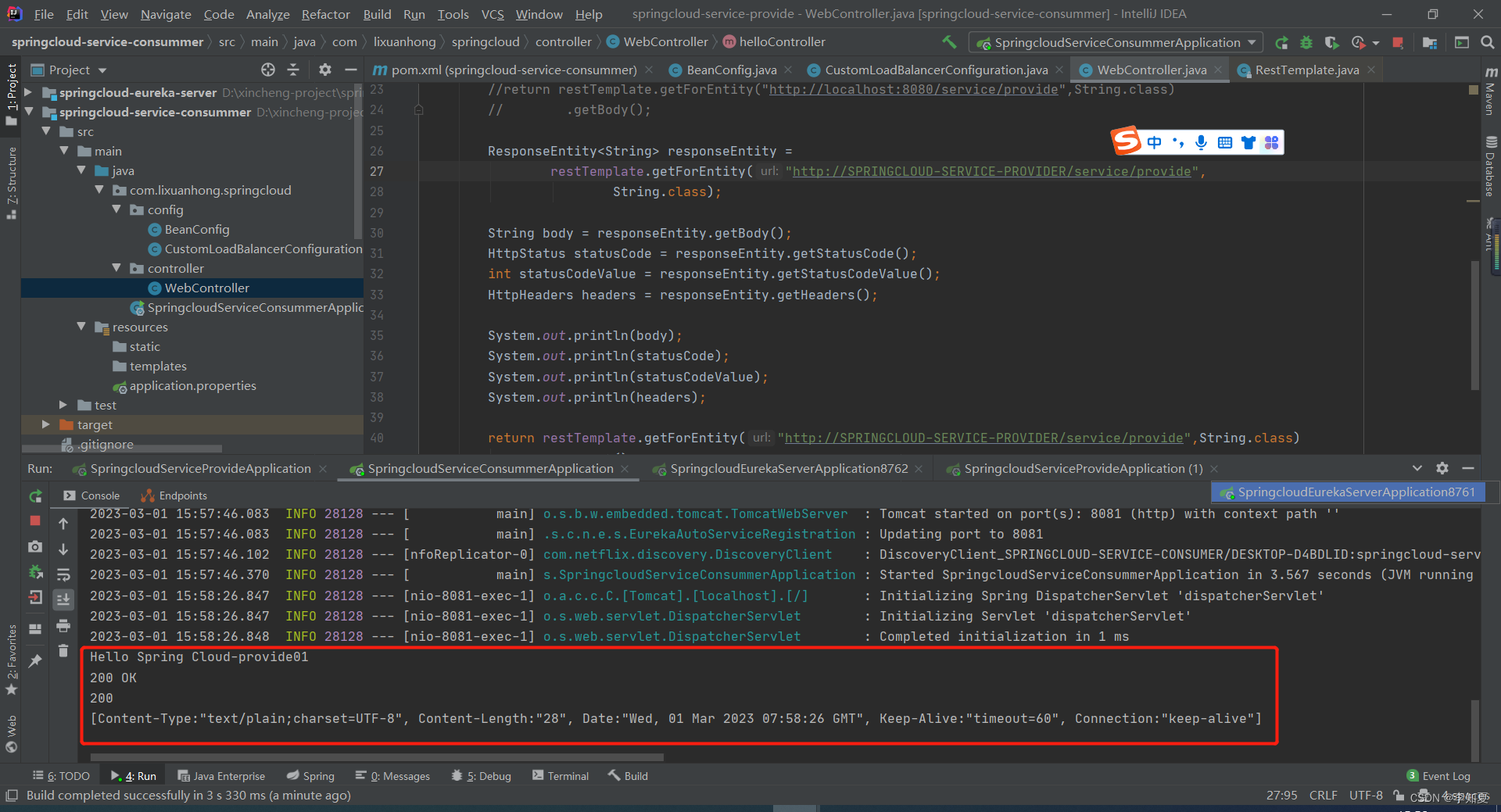
4-1 SpringCloud快速开发入门:RestTemplate类详细解读
RestTemplate类详细解读 RestTemplate 的 GET 请求 Get 请求可以有两种方式: 第一种:getForEntity 该方法返回一个 ResponseEntity对象,ResponseEntity是 Spring 对 HTTP 请求响应的封装,包括了几个重要的元素,比如响…...
【IDEA】【工具】幸福感UP!开发常用的工具 插件/网站/软件
IDEA 插件 CodeGlance Pro —— 代码地图 CodeGlance是一款非常好用的代码地图插件,可以在代码编辑区的右侧生成一个竖向可拖动的代码缩略区,可以快速定位代码的同时,并且提供放大镜功能。 使用:可以通过Settings—>Other Settings—&g…...

【蓝桥杯集训·每日一题】AcWing 1562. 微博转发
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴宽搜BFS一、题目 1、原题链接 1562. 微博转发 2、题目描述 微博被称为中文版的 Twitter。 微博上的用户既可能有很多关注者,也可能关注很多其他用户。 因此&am…...
[busybox] busybox生成一个最精简rootfs(下)
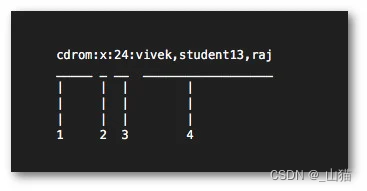
书接上回:[busybox] busybox生成一个最精简rootfs(上) 本篇介绍几个rootfs中用到的“不是那么重要的”几个文件。 9 /etc/shadow 和 /etc/passwd 曾经,/etc/passwd 文件用于存储独立 Linux 系统中的所有登录信息。 后来,由于以下原因&…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
