机器学习之K-means原理详解、公式推导、简单实例(python实现,sklearn调包)
目录
- 1. 聚类原理
- 1.1. 无监督与聚类
- 1.2. K均值算法
- 2. 公式推导
- 2.1. 距离
- 2.2. 最小平方误差
- 3. 实例
- 3.1. python实现
- 3.2. sklearn实现
- 4. 运行(可直接食用)
1. 聚类原理
1.1. 无监督与聚类
在这部分我今天主要介绍K均值聚类算法,在这之前我想提一下“无监督学习”和“聚类”。
无监督学习是指训练样本的标记信息是未知的,目标是通过对无标记训练样本的学习来揭示数据的内在性质和规律的学习。
在 sklearn 官网首页中,非常贴心的将任务分为了分类,回归,聚类三类,以此我们可以看出聚类的重要性。实际上聚类就是把训练集中的样本划分为通常不相交的几个子集,每个子集称为一个簇,每个簇对应的名字聚类事先是不知道的,需要靠使用者来把握命名。
优点
简单有效
缺点
对于K均值算法来说,最明显的缺点有很多:一开始定中心点数量需要人为定;中心点选取初始样本是随机选的。很多K均值优化算法都是从这几个方面入手改进的。
1.2. K均值算法
对于K均值算法,西瓜书的伪代码其实已经说的很明白了:

简单的说就是三步:
- 选择初始中心点,最基本的方法是从数据集中选择样本。初始化后,K-means由其他两个步骤之间的循环组成。
- 将每个样本指定给其最近的中心。
- 通过获取分配给每个先前中心的所有样本的平均值来创建新的中心。计算新旧质心之间的差值,算法重复最后两个步骤,直到该值小于阈值。
一般来说,中心点不会是已经存在的点,一般都是算出来的虚构的点。
提一下 对于高维数据,我们知道存在维度诅咒这一说法,所以在很多时候聚类往往会跟PCA之类的降维算法搭配。在降维算法中 TSNE 因为能将数据降维至2-3维,非常适合可视化,而且降维效率也高,所以也很常用。
2. 公式推导
2.1. 距离
简单的说,对于每个簇来说,簇内相似度高,簇外相似度低(高内距,低耦合)。那么衡量距离的方法有哪些?
- 曼哈顿距离
- 欧式距离
- 闵可夫斯基距离 distmk(xi,xj)=(∑u=1n∣xiu−xju∣p)1pdist_mk(x_i,x_j)=(\sum_{u=1}^n|{x_{iu}-x_{ju}|^p})^{\frac{1}{p}}distmk(xi,xj)=(∑u=1n∣xiu−xju∣p)p1
- 余弦相似度 cos(θ)=∑i=1n(xi×yi)∑i=1n(xi)2×∑i=1n(yi)2cos(\theta)=\frac{\sum_{i=1}^n(x_i\times y_i)}{\sqrt{\sum^n_{i=1}{(x_i)^2}} \times \sqrt{\sum^n_{i=1}{(y_i)^2}}}cos(θ)=∑i=1n(xi)2×∑i=1n(yi)2∑i=1n(xi×yi)
- 等等
注:p=1,闵可夫斯基距离为曼哈顿距离;p=2,闵可夫斯基距离为欧氏距离。
2.2. 最小平方误差
说白了就是每个簇内每个点到中心点的距离的和最小。
E=∑i=1k∑x∈Ci∣∣x−μi∣∣22E = \sum^k_{i=1}{\sum_{x\in C_i}{||x-\mu_i||_2^2}} E=i=1∑kx∈Ci∑∣∣x−μi∣∣22
μi\mu_iμi就是中心点,数学公式表示就是
μi=1∣Ci∣∑x∈Cix\mu_i=\frac{1}{|C_i|}\sum_{x\in C_i}{x} μi=∣Ci∣1x∈Ci∑x
3. 实例
西瓜数据集4.0为例
密度,含糖率
0.697,0.46
0.774,0.376
0.634,0.264
0.608,0.318
0.556,0.215
0.403,0.237
0.481,0.149
0.437,0.211
0.666,0.091
0.243,0.267
0.245,0.057
0.343,0.099
0.639,0.161
0.657,0.198
0.36,0.37
0.593,0.042
0.719,0.103
0.359,0.188
0.339,0.241
0.282,0.257
0.748,0.232
0.714,0.346
0.483,0.312
0.478,0.437
0.525,0.369
0.751,0.489
0.532,0.472
0.473,0.376
0.725,0.445
0.446,0.459
3.1. python实现
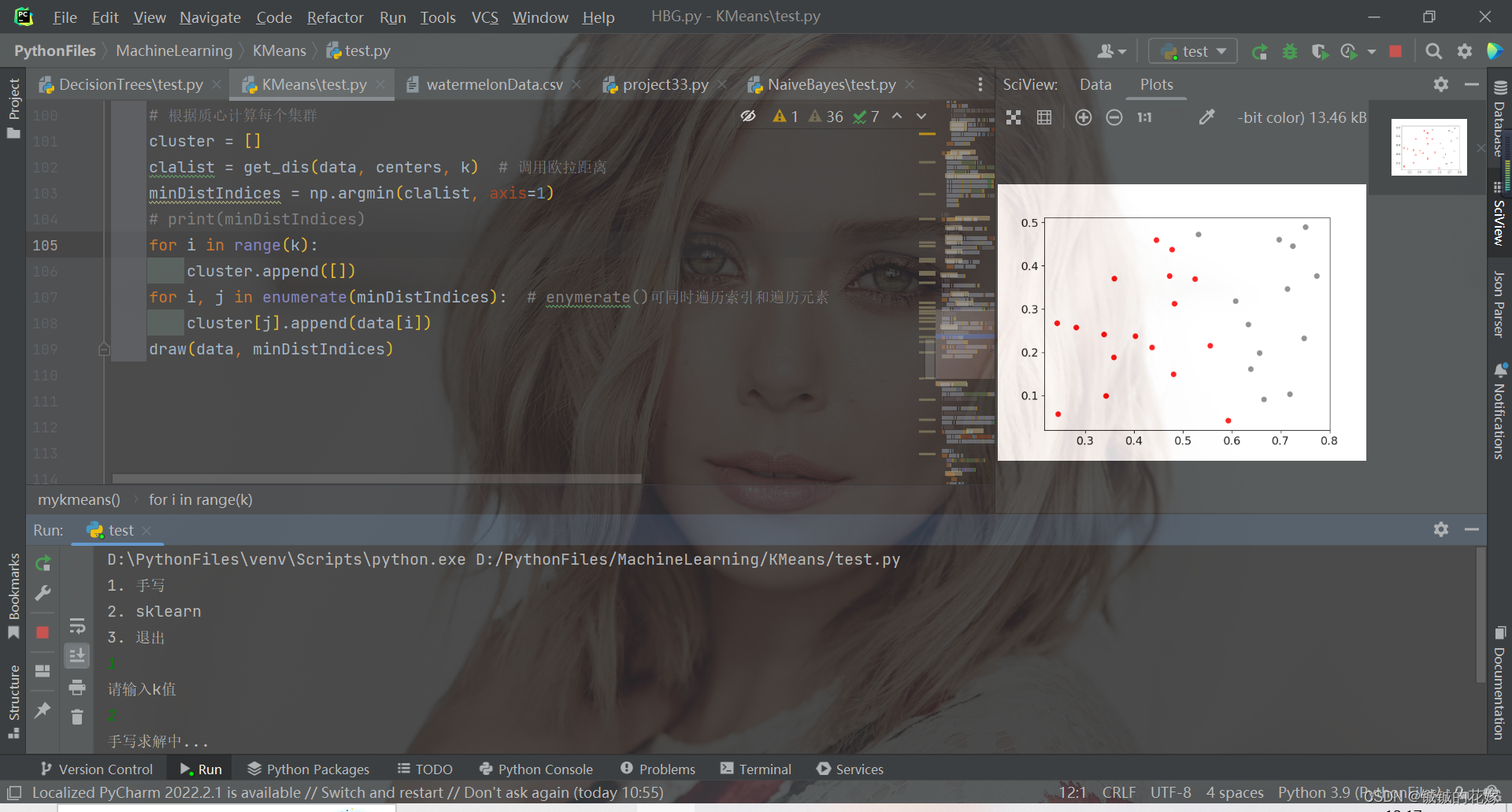
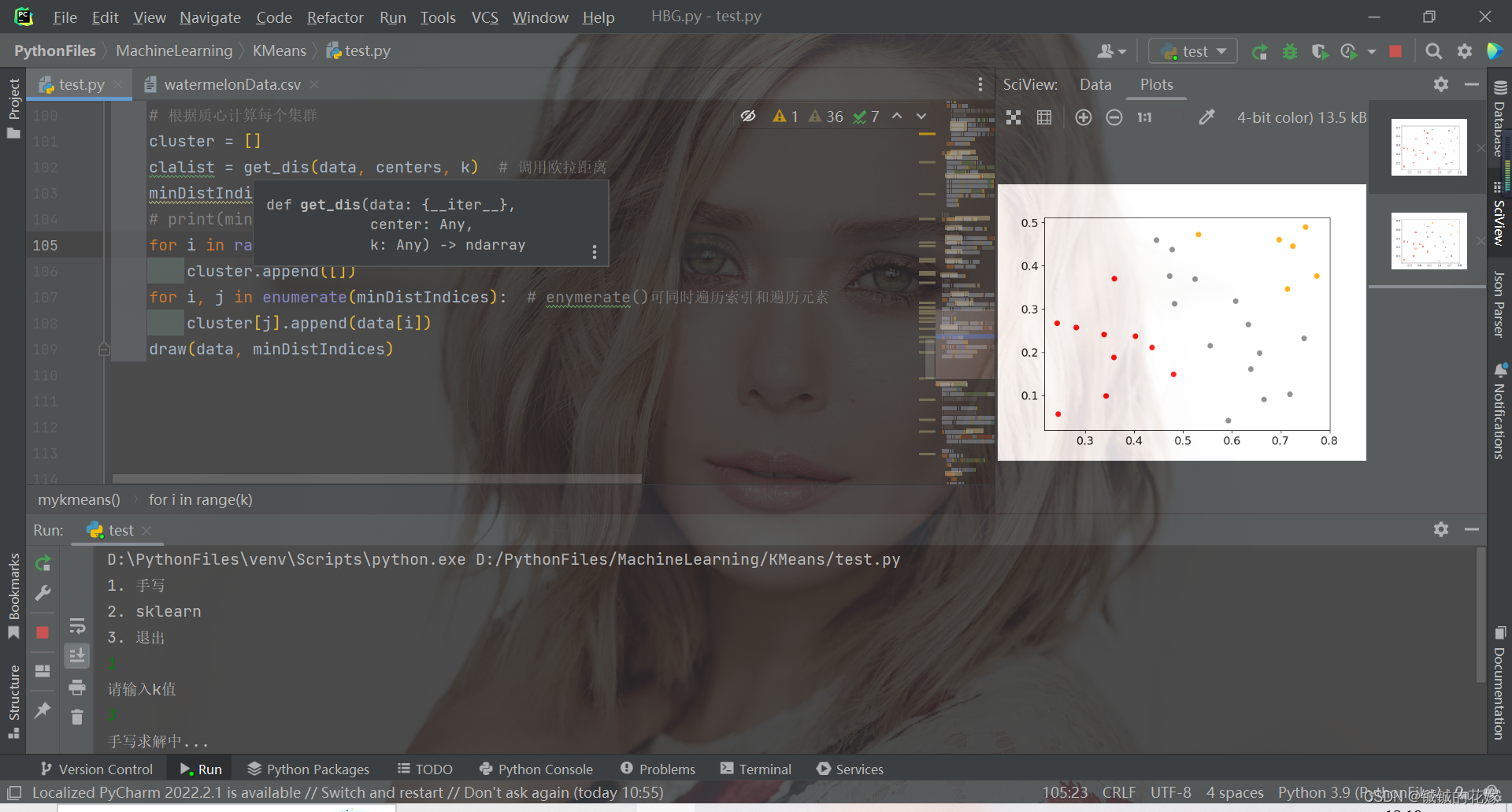
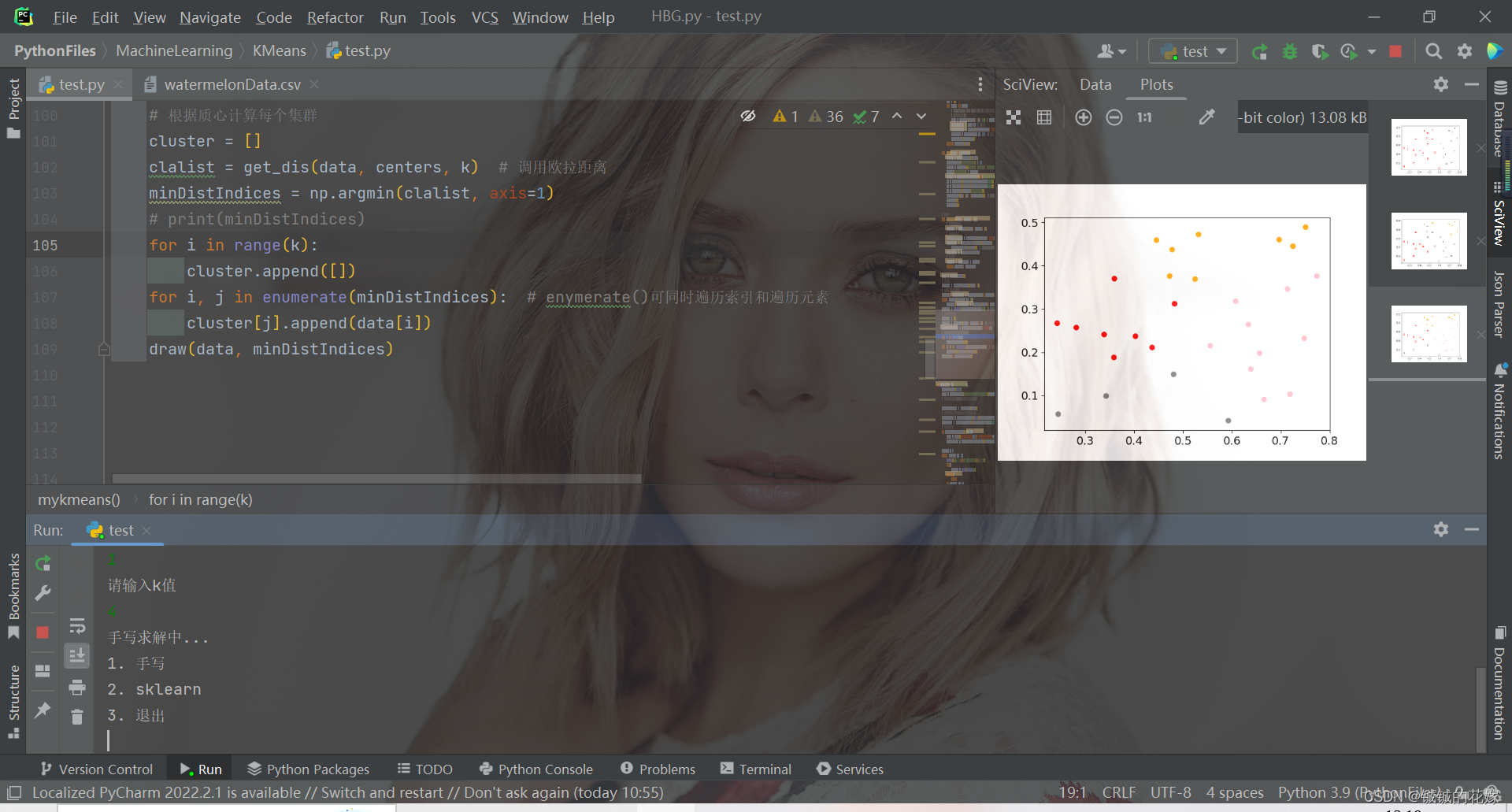
def mykmeans(data, k):# 计算距离def get_dis(data, center, k):ret = []for point in data:# np.tile(a, (2, 1))就是把a先沿x轴复制1倍,即没有复制,仍然是[0, 1, 2]。 再把结果沿y方向复制2倍得到array([[0, 1, 2], [0, 1, 2]])# k个中心点,所以有k行diff = np.tile(point, (k, 1)) - centersquaredDiff = diff ** 2 # 平方squaredDist = np.sum(squaredDiff, axis=1) # 和 (axis=1表示行)distance = squaredDist ** 0.5 # 开根号ret.append(distance)return np.array(ret)def draw(data, cluster):D_data = pd.DataFrame(data)plt.rcParams["font.size"] = 14colors = np.array(["red", "gray", "orange", "pink", "blue", "green"])D_data["cluster"] = clusterD_data = D_data.sort_values(by="cluster")xx = np.array(D_data[D_data.columns[0]]) # 取前两个维度可视化yy = np.array(D_data[D_data.columns[1]])cc = np.array(D_data["cluster"])plt.scatter(xx, yy, c=colors[cc]) # c=colors[cc]plt.show()plt.close()# 计算质心def classify(data, center, k):# 计算样本到质心的距离clalist = get_dis(data, center, k)# 分组并计算新的质心minDistIndices = np.argmin(clalist, axis=1) # axis=1 表示求出每行的最小值的下标newCenter = pd.DataFrame(data).groupby(minDistIndices).mean() # DataFramte(dataSet)对DataSet分组,groupby(min)按照min进行统计分类,mean()对分类结果求均值newCenter = newCenter.values# 计算变化量changed = newCenter - centerreturn changed, newCenterdata = data.tolist()# 随机取质心centers = random.sample(data, k)# 更新质心 直到变化量全为0changed, newCenters = classify(data, centers, k)while np.any(changed != 0):changed, newCenters = classify(data, newCenters, k)centers = sorted(newCenters.tolist()) # tolist()将矩阵转换成列表 sorted()排序# 根据质心计算每个集群cluster = []clalist = get_dis(data, centers, k) # 调用欧拉距离minDistIndices = np.argmin(clalist, axis=1)print(minDistIndices)for i in range(k):cluster.append([])for i, j in enumerate(minDistIndices): # enymerate()可同时遍历索引和遍历元素cluster[j].append(data[i])draw(data, minDistIndices)3.2. sklearn实现
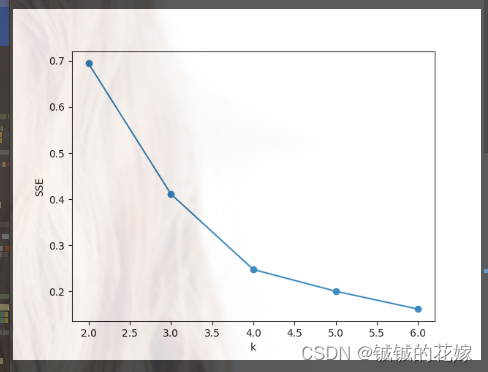
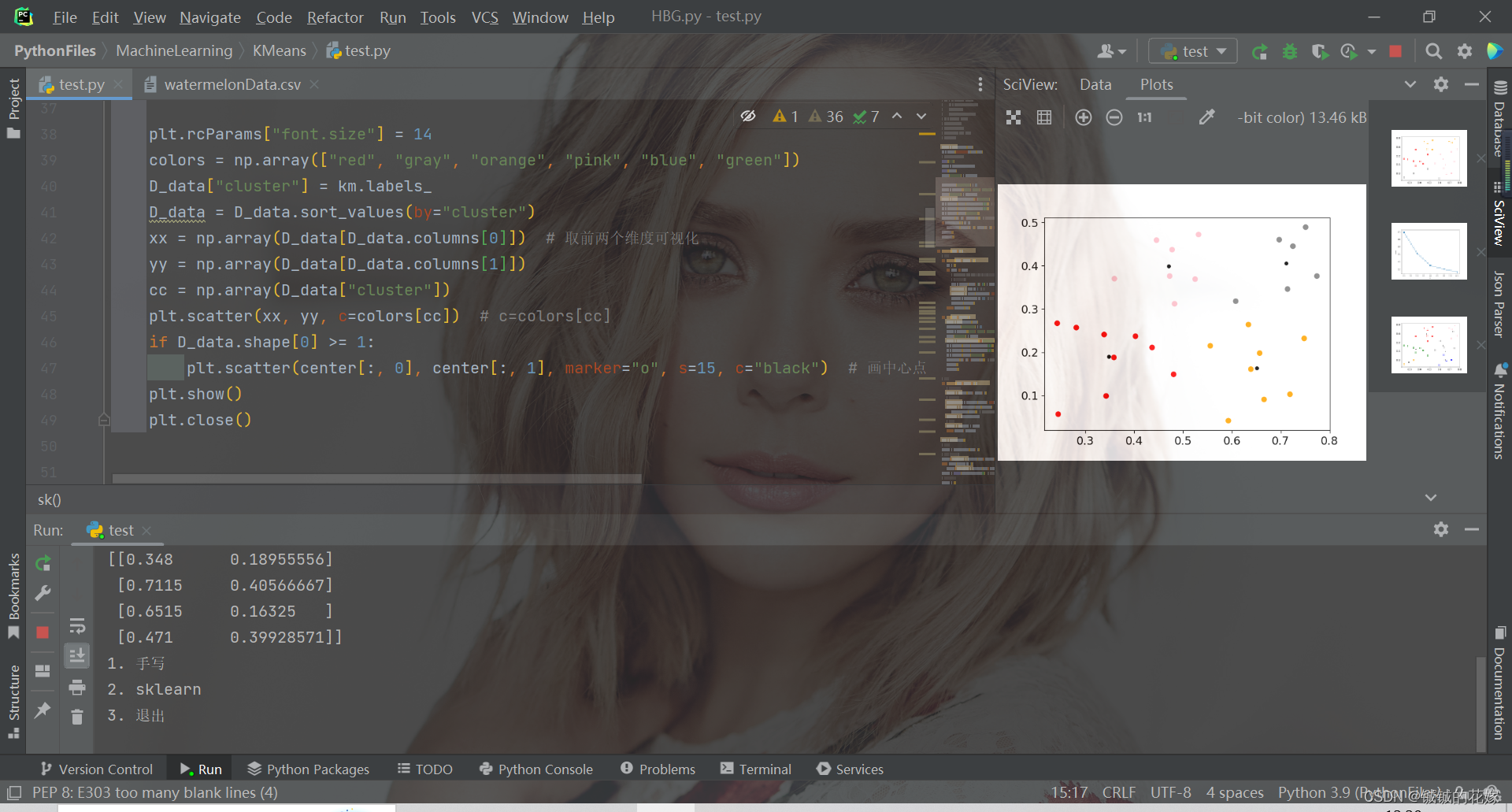
def sk(data, k):# # 肘部法取k值# data = np.array(data)# SSE = []# right = min(7, data.shape[0])# for k in range(2, right):# km = KMeans(n_clusters=k)# km.fit(data)# SSE.append(km.inertia_)# xx = range(2, right)# plt.xlabel("k")# plt.ylabel("SSE")# plt.plot(xx, SSE, "o-")# plt.show()D_data = pd.DataFrame(data)km = KMeans(n_clusters=k).fit(data)# print(km.labels_)print("质心")center = km.cluster_centers_print(center)D_data["cluster"] = km.labels_plt.rcParams["font.size"] = 14colors = np.array(["red", "gray", "orange", "pink", "blue", "green"])D_data["cluster"] = km.labels_D_data = D_data.sort_values(by="cluster")xx = np.array(D_data[D_data.columns[0]]) # 取前两个维度可视化yy = np.array(D_data[D_data.columns[1]])cc = np.array(D_data["cluster"])plt.scatter(xx, yy, c=colors[cc]) # c=colors[cc]if D_data.shape[0] >= 1:plt.scatter(center[:, 0], center[:, 1], marker="o", s=15, c="black") # 画中心点plt.show()plt.close()4. 运行(可直接食用)
import random
from collections import Counter
import numpy as np
import pandas as pd
import warnings
from matplotlib import pyplot as plt
from sklearn.cluster import KMeans
from sklearn.manifold import TSNEwarnings.filterwarnings("ignore")def sk(data, k):# # 肘部法取k值# data = np.array(data)# SSE = []# right = min(7, data.shape[0])# for k in range(2, right):# km = KMeans(n_clusters=k)# km.fit(data)# SSE.append(km.inertia_)# xx = range(2, right)# plt.xlabel("k")# plt.ylabel("SSE")# plt.plot(xx, SSE, "o-")# plt.show()D_data = pd.DataFrame(data)km = KMeans(n_clusters=k).fit(data)# print(km.labels_)print("质心")center = km.cluster_centers_print(center)D_data["cluster"] = km.labels_plt.rcParams["font.size"] = 14colors = np.array(["red", "gray", "orange", "pink", "blue", "green"])D_data["cluster"] = km.labels_D_data = D_data.sort_values(by="cluster")xx = np.array(D_data[D_data.columns[0]]) # 取前两个维度可视化yy = np.array(D_data[D_data.columns[1]])cc = np.array(D_data["cluster"])plt.scatter(xx, yy, c=colors[cc]) # c=colors[cc]if D_data.shape[0] >= 1:plt.scatter(center[:, 0], center[:, 1], marker="o", s=15, c="black") # 画中心点plt.show()plt.close()def mykmeans(data, k):# 计算距离def get_dis(data, center, k):ret = []for point in data:# np.tile(a, (2, 1))就是把a先沿x轴复制1倍,即没有复制,仍然是[0, 1, 2]。 再把结果沿y方向复制2倍得到array([[0, 1, 2], [0, 1, 2]])# k个中心点,所以有k行diff = np.tile(point, (k, 1)) - centersquaredDiff = diff ** 2 # 平方squaredDist = np.sum(squaredDiff, axis=1) # 和 (axis=1表示行)distance = squaredDist ** 0.5 # 开根号ret.append(distance)return np.array(ret)def draw(data, cluster):D_data = pd.DataFrame(data)plt.rcParams["font.size"] = 14colors = np.array(["red", "gray", "orange", "pink", "blue", "green"])D_data["cluster"] = clusterD_data = D_data.sort_values(by="cluster")xx = np.array(D_data[D_data.columns[0]]) # 取前两个维度可视化yy = np.array(D_data[D_data.columns[1]])cc = np.array(D_data["cluster"])plt.scatter(xx, yy, c=colors[cc]) # c=colors[cc]plt.show()plt.close()# 计算质心def classify(data, center, k):# 计算样本到质心的距离clalist = get_dis(data, center, k)# 分组并计算新的质心minDistIndices = np.argmin(clalist, axis=1) # axis=1 表示求出每行的最小值的下标newCenter = pd.DataFrame(data).groupby(minDistIndices).mean() # DataFramte(dataSet)对DataSet分组,groupby(min)按照min进行统计分类,mean()对分类结果求均值newCenter = newCenter.values# 计算变化量changed = newCenter - centerreturn changed, newCenterdata = data.tolist()# 随机取质心centers = random.sample(data, k)# 更新质心 直到变化量全为0changed, newCenters = classify(data, centers, k)while np.any(changed != 0):changed, newCenters = classify(data, newCenters, k)centers = sorted(newCenters.tolist()) # tolist()将矩阵转换成列表 sorted()排序# 根据质心计算每个集群cluster = []clalist = get_dis(data, centers, k) # 调用欧拉距离minDistIndices = np.argmin(clalist, axis=1)# print(minDistIndices)for i in range(k):cluster.append([])for i, j in enumerate(minDistIndices): # enymerate()可同时遍历索引和遍历元素cluster[j].append(data[i])draw(data, minDistIndices)if __name__ == '__main__':random.seed(1129)data = pd.read_csv("watermelonData.csv").sample(frac=1, random_state=1129)# 因为西瓜数据集每列都是0到1的,所以这里就不进行标准化了data_shuffled = np.array(data)# 划分训练集测试集,感觉不太需要测试集,直接把比例拉到1data_train = data_shuffled[:int(data_shuffled.shape[0]*1), :]data_test = data_shuffled[data_train.shape[0]:, :]# 维度上去了就降维if data_train.shape[1]>10:tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=5000, method='exact', random_state=0)data_train = tsne.fit_transform(data_train)choice = 0while choice != 3:print("1. 手写\n2. sklearn\n3. 退出")try:choice = int(input())except:breakif choice == 1:print("请输入k值")try:k = int(input())except:breakprint("手写求解中...")# 参考:https://blog.csdn.net/qq_43741312/article/details/97128745# 主要是发现了很多np和pd在计算的时候的用法mykmeans(data_train, k)elif choice == 2:print("请输入k值")try:k = int(input())except:breakprint('sklearn yyds')sk(data_train, k)else:print("退出成功")choice = 3break参考:
吴恩达《机器学习》
sklearn官网
《百面机器学习》
相关文章:

机器学习之K-means原理详解、公式推导、简单实例(python实现,sklearn调包)
目录1. 聚类原理1.1. 无监督与聚类1.2. K均值算法2. 公式推导2.1. 距离2.2. 最小平方误差3. 实例3.1. python实现3.2. sklearn实现4. 运行(可直接食用)1. 聚类原理 1.1. 无监督与聚类 在这部分我今天主要介绍K均值聚类算法,在这之前我想提一…...

OBS 进阶 一个从自定义对话框中 传参到插件的例子
目录 一、自定义对话框,传参综合例子 1、自定义对话框 1)自定义对话框类...
在Linux和Windows上编译datax-web-ui源码
记录:375场景:在CentOS 7.9操作系统上,使用apache-maven-3.8.7安装编译datax-web-ui源码。在Windows上操作系统上,使用apache-maven-3.8.7编译datax-web-ui源码。版本:JDK 1.8 node-v14.17.3 npm-6.14.13datax-web-ui开…...

React组件生命周期管理
组件生命,就是组件在不同阶段提供对应的钩子函数,来处理逻辑操作。比如初始化阶段,我们需要初始化组件相关的状态和变量。组件销毁阶段时,我们需要把一些数据结构销毁来节约内存。 React组件生命周期 React组件生命周期分为三个阶段:挂载阶段【Mount】、更新阶段【Updat…...

Linux:全志H3图像codec使用笔记
1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. 图像 codec 概述 图像编解码器(codec) 包含 Encoder 和 Decoder 两部分功能。我们用下列分别说明 Encoder 和 Decoder 的工作方式。 ----------…...

【Python小游戏】通过这款专为程序员设计的《极限车神》小游戏,你的打字速度可以赢过专业录入员,这个秘密98%的人都不知道哦~(爆赞)
导语 哈喽,我是你们的木木子👸! 今天小编要为大家介绍一款小编自己用代码码出来的赛车风格的打字小游戏 取名暂定为《🚗极限车神🚗》打字小游戏。 这款Pygame小游戏在玩法上可以说十分创新,不仅能游戏还…...
Springboot扩展点之BeanPostProcessor
前言 Springboot(Spring)的扩展点其实有很多,但是都有一个共同点,都是围绕着Bean和BeanFactory(容器)展开的,其实这也很好理解,Spring的核心是控制反转、依赖注入、面向切面编程&…...

Fluent Python 笔记 第 3 章 字典和集合
3.1 泛映射类型 只有可散列 的数据类型才能用作这些映射里的键 字典构造方法: >>> a dict(one1, two2, three3) >>> b {one: 1, two: 2, three: 3} >>> c dict(zip([one, two, three], [1, 2, 3])) >>> d dict([(two, 2…...
大型物流运输管理系统源码 TMS源码
大型物流运输管理系统源码 TMS是一套适用于物流公司的物流运输管理系统,涵盖物流公司内部从订单->提货->运单->配车->点到->预约->签收->回单->代收货款的全链条管理系统。 菜单功能 一、运营管理 1、订单管理:用于客户意向订…...
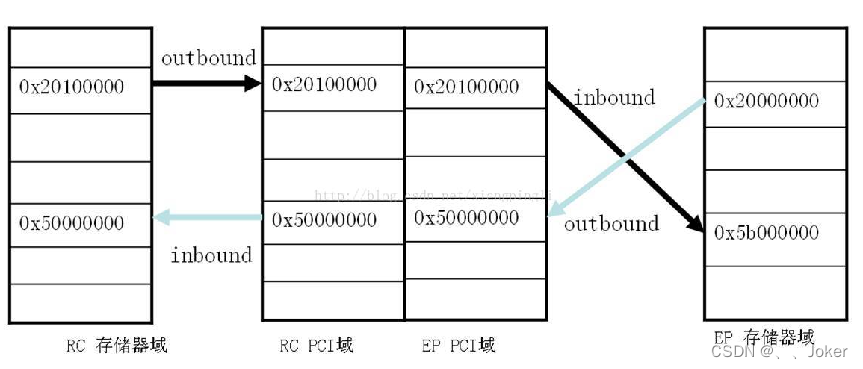
PCIE总线
PCIE总线记录描述PCI分类与速度PCIE连接拓扑与角色PCIE接口定义PCIE数据传输方式与中断在PCIE中有两种数据传输方式:PCIE中断:PCIE协议栈与工作流程PCIE地址空间分类实例分析PCIE两种访问方式描述 PCI-Express(peripheral component interconnect expre…...

Android IO 框架 Okio 的实现原理,如何检测超时?
本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。 前言 大家好,我是小彭。 在上一篇文章里,我们聊到了 Square 开源的 I/O 框架 Okio 的三个优势:精简且全面的 API、基于共享的缓冲区设计以…...

简单介绍反射
1.定义Java的反射机制是在运行状态中,对于任意一个类,都知道这个类的所有属性和方法;对于任意一个对象,都能调用它的任意方法和属性,既然能拿到,我们就可以修改部分类型信息;这种动态获取信息的…...

PyTorch学习笔记:nn.MSELoss——MSE损失
PyTorch学习笔记:nn.MSELoss——MSE损失 torch.nn.MSELoss(size_average None,reduce None,reduction mean)功能:创建一个平方误差(MSE)损失函数,又称为L2损失: l(x,y)L{l1,…,lN}T,ln(xn−yn)2l(x,y)L…...
apache和nginx的TLS1.0和TLS1.1禁用处理方案
1、TLS1.0和TLS1.1是什么? TLS协议其实就是网络安全传输层协议,用于在两个通信应用程序之间提供保密性和数据完整性,TLS 1. 0 和TLS 1. 1 是分别是96 年和 06 年发布的老版协议。 2、为什么要禁用TLS1.0和TLS1.1传输协议 TLS1.0和TLS1.1协…...
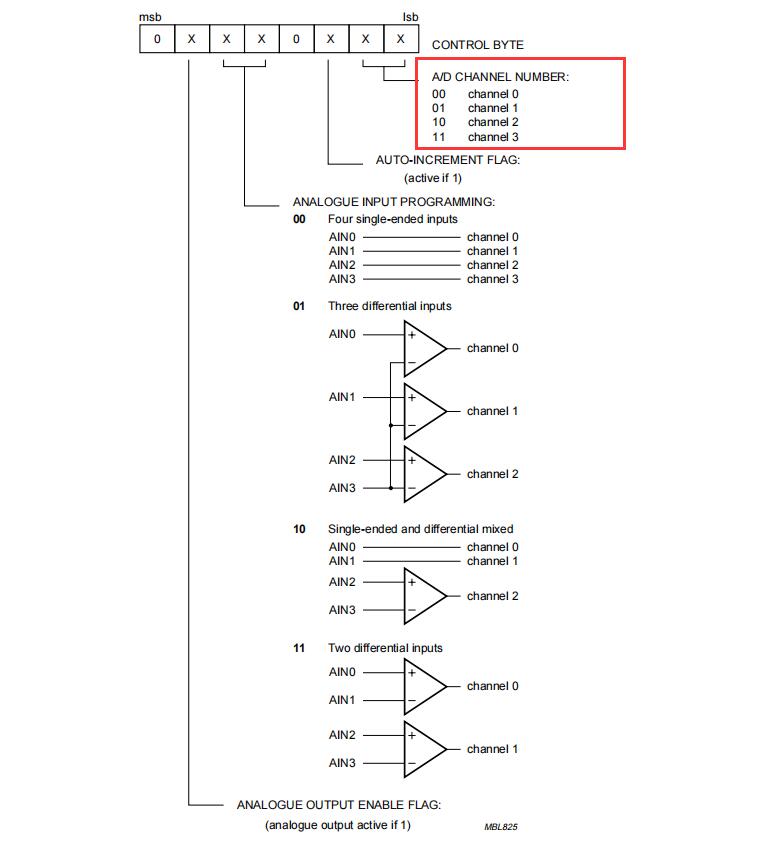
K_A12_002 基于STM32等单片机采集光敏电阻传感器参数串口与OLED0.96双显示
K_A12_002 基于STM32等单片机采集光敏电阻传感器参数串口与OLED0.96双显示一、资源说明二、基本参数参数引脚说明三、驱动说明IIC地址/采集通道选择/时序对应程序:四、部分代码说明1、接线引脚定义1.1、STC89C52RC光敏电阻传感器模块1.2、STM32F103C8T6光敏电阻传感器模块五、基…...

《机器学习》学习笔记
第 2 章 模型评估与选择 2.1 经验误差与过拟合 精度:精度1-错误率。如果在 mmm 个样本中有 aaa 个样本分类错误,则错误率 Ea/mEa/mEa/m,精度 1−a/m1-a/m1−a/m。误差:一般我们把学习器的实际预测输出与样本的真实输出之间的差…...
前端卷算法系列(一)
前端卷算法系列(一) 两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同…...

【机器学习】聚类算法(理论)
聚类算法(理论) 目录一、概论1、聚类算法的分类2、欧氏空间的引入二、K-Means算法1、算法思路2、算法总结三、DBSCAN算法1、相关概念2、算法思路3、算法总结四、实战部分一、概论 聚类分析,即聚类(Clustering)…...
Docker-用Jenkins发版Java项目-(1)Docke安装Jenkins
文章目录前言环境背景操作流程docker安装及jenkins软件安装jenkins配置登录配置安装插件及创建账号前言 学海无涯,旅“途”漫漫,“途”中小记,如有错误,敬请指出,在此拜谢! 最近新购得了M2的MAC,…...
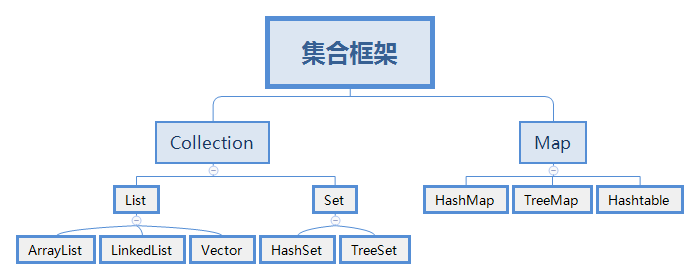
java集合框架内容整理
主要内容集合框架体系ArrayListLinkedListHashSetTreeSetLinkedHashSet内部比较器和外部比较器哈希表的原理List集合List集合的主要实现类有ArrayList和LinkedList,分别是数据结构中顺序表和链表的实现。另外还包括栈和队列的实现类:Deque和Queue。• Li…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
