AcWing算法提高课-3.1.2信使
宣传一下算法提高课整理 <—
CSDN个人主页:更好的阅读体验 <—

题目传送门点这里
题目描述
战争时期,前线有 nnn 个哨所,每个哨所可能会与其他若干个哨所之间有通信联系。
信使负责在哨所之间传递信息,当然,这是要花费一定时间的(以天为单位)。
指挥部设在第一个哨所。
当指挥部下达一个命令后,指挥部就派出若干个信使向与指挥部相连的哨所送信。
当一个哨所接到信后,这个哨所内的信使们也以同样的方式向其他哨所送信。信在一个哨所内停留的时间可以忽略不计。
直至所有 nnn 个哨所全部接到命令后,送信才算成功。
因为准备充足,每个哨所内都安排了足够的信使(如果一个哨所与其他 k 个哨所有通信联系的话,这个哨所内至少会配备 kkk 个信使)。
现在总指挥请你编一个程序,计算出完成整个送信过程最短需要多少时间。
输入格式
第 111 行有两个整数 nnn 和 mmm,中间用 111 个空格隔开,分别表示有 nnn 个哨所和 mmm 条通信线路。
第 222 至 m+1m+1m+1 行:每行三个整数 i、j、ki、j、ki、j、k,中间用 111 个空格隔开,表示第 iii 个和第 jjj 个哨所之间存在 双向 通信线路,且这条线路要花费 kkk 天。
输出格式
一个整数,表示完成整个送信过程的最短时间。
如果不是所有的哨所都能收到信,就输出-1。
数据范围
1≤n≤100,1≤n≤100,1≤n≤100,
1≤m≤200,1≤m≤200,1≤m≤200,
1≤k≤10001≤k≤10001≤k≤1000
样例输入
4 4
1 2 4
2 3 7
2 4 1
3 4 6
样例输出
11
题目化简:
给定一个 nnn 个点 mmm 条边的无向图,求编号为1的点与其他点之间最短距离的最大值。
思路
这道题因为数据范围极小,为了节约代码长度,可以采用Floyd算法。
在求出任意两点间最短距离之后,遍历dist[1][i],求出最大值。
Dijkstra算法与Floyd类似,代码部分也给出了朴素Dijkstra和堆优化Dijkstra的代码。
算法时间复杂度
如果采用Floyd算法,那么时间复杂度是O(n3)O(n^3)O(n3);
朴素Dijkstra算法:O(n2)O(n^2)O(n2), 但是代码较长;
堆优化Dijkstra算法:O(mlogn)O(m \log n)O(mlogn),同样的代码较长
AC Code
C++(Floyd)C++ (Floyd)C++(Floyd)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110, inf = 1e9;int n, m;
int d[N][N];void init()
{for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )if (i == j) d[i][j] = 0;else d[i][j] = inf;
}void floyd()
{for (int k = 1; k <= n; k ++ )for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}int main()
{cin >> n >> m;init();while (m -- ){int a, b, c;cin >> a >> b >> c;d[a][b] = min(d[a][b], c);d[b][a] = min(d[b][a], c);}floyd();int res = 0;for (int i = 2; i <= n; i ++ )res = max(res, d[1][i]);if (res == inf) puts("-1");else printf("%d\n", res);return 0;
}
C++(朴素Dijkstra)C++ (朴素Dijkstra)C++(朴素Dijkstra)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110;int n, m;
int g[N][N];
int dist[N];
bool st[N];int dijkstra()
{int res = 0;memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 1; i <= n; i ++ ){int t = -1;for (int j = 1; j <= n; j ++ )if (!st[j] &&(t == -1 || dist[t] > dist[j]))t = j;st[t] = true;res = max(res, dist[t]);for (int j = 1; j <= n; j ++ )dist[j] = min(dist[j], dist[t] + g[t][j]);}return res == 0x3f3f3f3f ? -1 : res;
}
int main()
{memset(g, 0x3f, sizeof g);scanf("%d%d", &n, &m);while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = g[b][a] = min(g[a][b], c);}cout << dijkstra() << endl;return 0;
}
C++(堆优化Dijkstra)C++ (堆优化Dijkstra)C++(堆优化Dijkstra)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>#define x first
#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 110, M = N << 2;int n, m;
int h[N], e[M], w[M], ne[M], idx;
int dist[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra()
{int res = 0, cnt = 0;memset(dist, 0x3f, sizeof dist);dist[1] = 0;priority_queue<PII, vector<PII>, greater<>> heap;heap.push({0, 1});while (!heap.empty()){PII u = heap.top();heap.pop();if (st[u.y]) continue;st[u.y] = true;res = max(res, u.x);cnt ++ ;for (int i = h[u.y]; ~i; i = ne[i]){int j = e[i];if (dist[j] > dist[u.y] + w[i]){dist[j] = dist[u.y] + w[i];heap.push({dist[j], j});}}}return cnt == n ? res : -1;
}
int main()
{memset(h, -1, sizeof h);scanf("%d%d", &n, &m);while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c), add(b, a, c);}cout << dijkstra() << endl;return 0;
}

最后,如果觉得对您有帮助的话,点个赞再走吧!
相关文章:

AcWing算法提高课-3.1.2信使
宣传一下算法提高课整理 <— CSDN个人主页:更好的阅读体验 <— 题目传送门点这里 题目描述 战争时期,前线有 nnn 个哨所,每个哨所可能会与其他若干个哨所之间有通信联系。 信使负责在哨所之间传递信息,当然,…...

Paddle OCR Win 11下的安装和简单使用教程
Paddle OCR Win 11下的安装和简单使用教程 对于中文的识别,可以考虑直接使用Paddle OCR,识别准确率和部署都相对比较方便。 环境搭建 目前PaddlePaddle 发布到v2.4,先下载paddlepaddle,再下载paddleocr。根据自己设备操作系统进…...

杂谈:数组index问题和对象key问题
面试题一: var arr [1, 2, 3, 4] 问:arr[1] ?; arr[1] ?答:arr[1] 2; arr[1] 2 这里可以再分为两个问题: 1、数组赋值 var arr [1, 2, 3, 4]arr[1] 10; // 数字场景 arr[10] 1; // 字符串场景 arr[a] 1; // 字符串…...
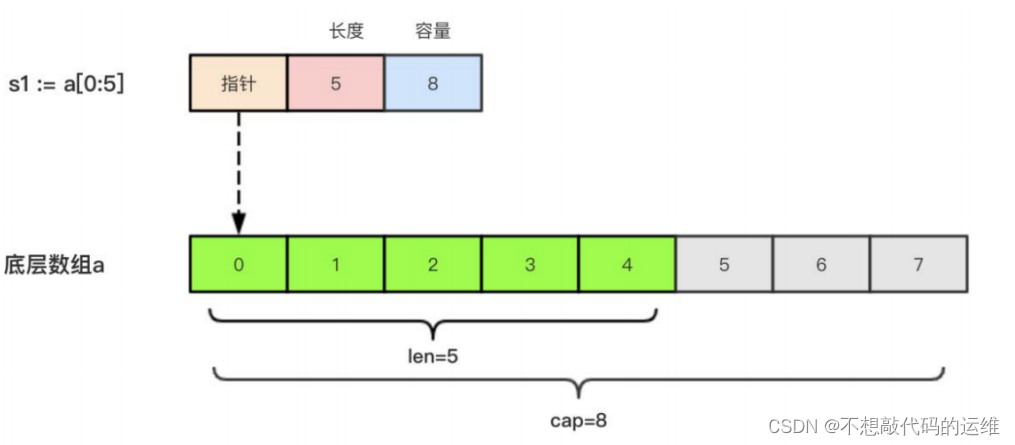
三天Golang快速入门—Slice切片
三天Golang快速入门—Slice切片Slice切片切片原理切片遍历append函数操作切片append添加append追加多个切片中删除元素切片合并string和slice的联系Slice切片 切片原理 由三个部分构成,指针、长度、容量指针:指向slice第一个元素对应的数组元素的地址长…...
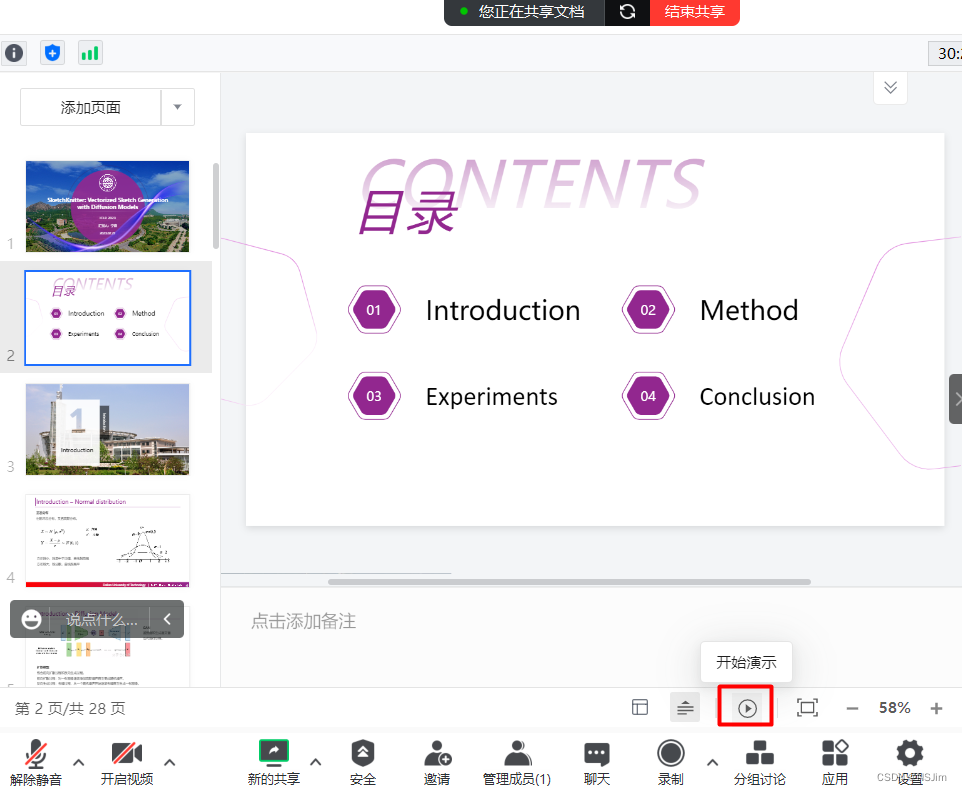
腾讯会议演示者视图/演讲者视图
前言 使用腾讯会议共享PPT时,腾讯会议支持共享用户使用演示者视图/演讲者视图,而会议其他成员可以看到正常的放映视图。下面以Win10系统和Office为例,介绍使用步骤。值得一提的是,该方法同时适用于单显示屏和多显示屏。 腾讯会议…...
【C++】类与对象(一)
文章目录1、面向过程和面向对象初步认识2、类的引入3、类的定义4、类的访问限定符5、类的作用域6、类的实例化7、计算类对象的大小8、this指针9、 C语言和C实现Stack的对比1、面向过程和面向对象初步认识 C语言是面向过程的,关注的是过程,分析出求解问题…...

JavaScript基本语法
本文提到的绝大多数语法都是与Java不同的语法,相同的就不会赘述了.JavaScript的三种引入方式内部js<body><script>alert(hello);</script> </body>行内js<body><div onclick"alert(hello)">这是一个div 点击一下试试</div>…...

OpenCV4.x图像处理实例-道路车辆检测(基于背景消减法)
通过背景消减进行道路车辆检测 文章目录 通过背景消减进行道路车辆检测1、车辆检测思路介绍2、BackgroundSubtractorMOG23、车辆检测实现在本文中,将介绍如何使用简单但有效的背景-前景减法方法执行车辆检测等任务。本文将使用 OpenCV 中使用背景-前景减法和轮廓检测,以及如何…...
pwnlab通关流程
pwnlab通关 关于文件包含,环境变量劫持的一个靶场 信息收集 靶机ip:192.168.112.133 开放端口 根据开放的端口信息决定从80web端口入手 目录信息 在images和upload路径存在目录遍历,config.php被渲染无法查看,upload.php需…...

面向过程与面向对象的区别与联系
目录 什么是面向过程 什么是面向对象 区别 各自的优缺点 什么是面向过程 面向过程是一种以事件为中心的编程思想,编程的时候把解决问题的步骤分析出来,然后用函数把这些步骤实现,在一步一步的具体步骤中再按顺序调用函数。 什么是面向对…...
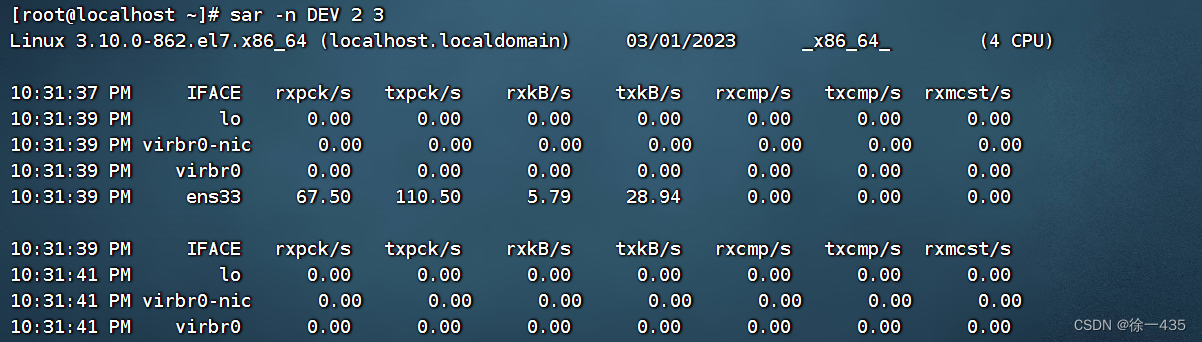
主机状态(查看资源占用情况、查看网络占用情况)
1. 查看资源占用情况 【1】可以通过top命令查看cpu、内存的使用情况,类似windows的任务管理器 默认5s刷新一次 语法:top 可 Ctrl c 退出 2.磁盘信息监控 【1】使用df命令,查看磁盘信息占用情况 语法:df [ -h ] 以更加人性化…...
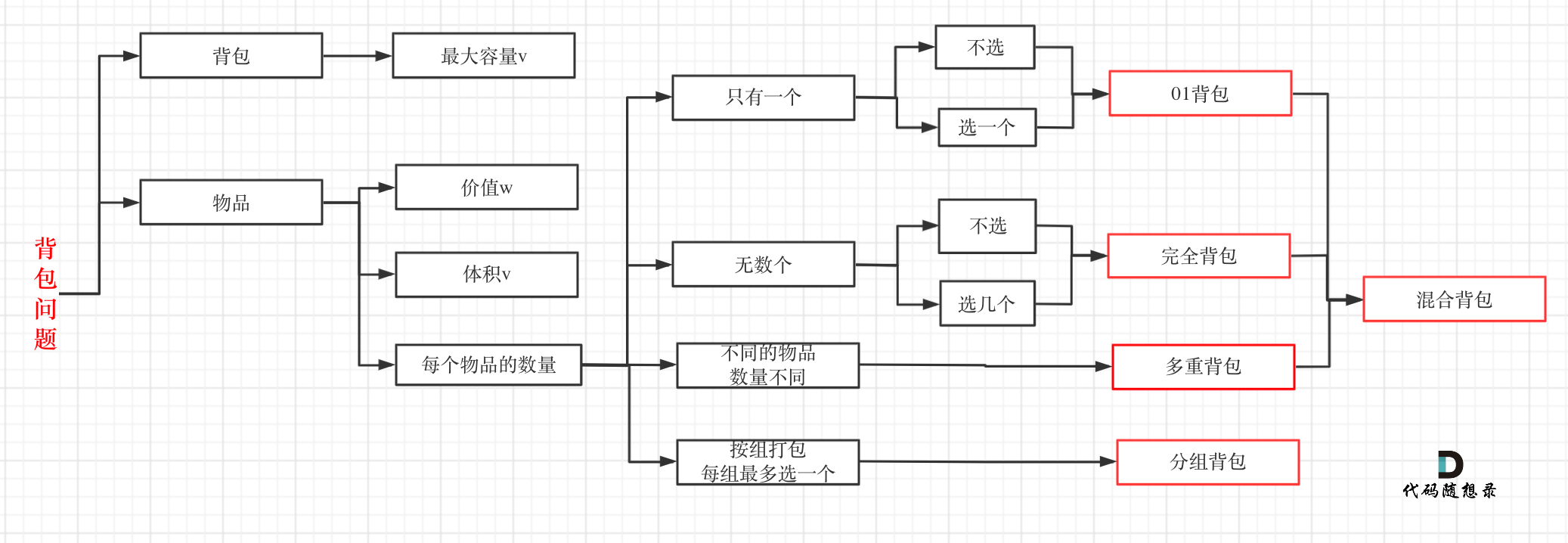
代码随想录算法训练营第四十一天 | 01背包问题-二维数组滚动数组,416. 分割等和子集
一、参考资料01背包问题 二维 https://programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.html 视频讲解:https://www.bilibili.com/video/BV1cg411g7Y6 01背包问题 一维 https://programmercarl.com/%E8%83%8C%E5…...

VMware NSX 4.1 发布 - 网络安全虚拟化平台
请访问原文链接:VMware NSX 4 - 网络安全虚拟化平台,查看最新版。原创作品,转载请保留出处。 作者主页:www.sysin.org VMware NSX 提供了一个敏捷式软件定义基础架构,用来构建云原生应用程序环境。NSX 专注于为具有异…...

计算理论 复杂度预备知识
文章目录计算理论 复杂度预备知识符号递归表达式求解通项公式主方法Akra-Bazzi 定理计算理论 复杂度预备知识 符号 f(n)o(g(n))f(n)o(g(n))f(n)o(g(n)) :∃c\exists c∃c ,当 nnn 足够大时, f(n)<cg(n)f(n)\lt cg(n)f(n)<cg(n) &#…...
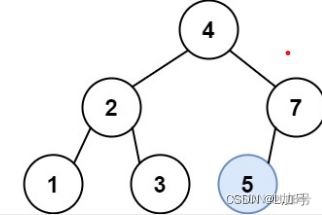
二叉树——二叉搜索树中的插入操作
二叉搜索树中的插入操作 链接 给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。 注意,…...

C# if break,if continue,if return的区别和使用
故事部分: 现在你肚子饿了,想要去: 1.吃个三菜一汤。 2.吃个蛋糕。 3.喝个奶茶。 结果,你吃饭的时候,吃到一个虫子。 你会有几种做法? 1.把有虫子这道菜拿走,继续吃下一道菜 。 2.算了ÿ…...

力扣-第二高的薪水
大家好,我是空空star,本篇带大家了解一道中等的力扣sql练习题。 文章目录前言一、题目:176. 第二高的薪水二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他总结…...
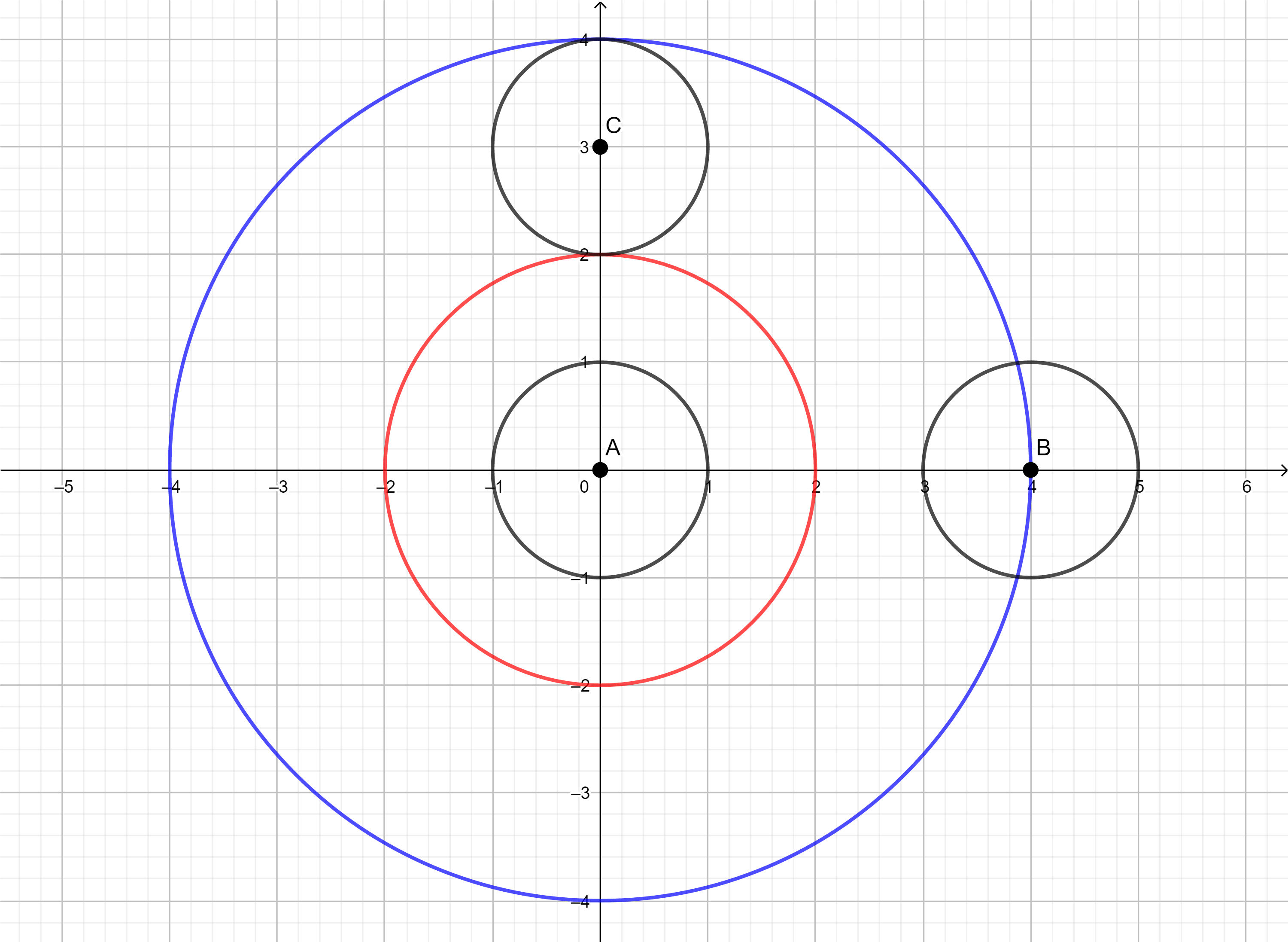
I - 太阳轰炸(组合数学Cnk n固定)
2023河南省赛组队训练赛(二) - Virtual Judge (vjudge.net) 背景:阿塔尼斯,达拉姆的大主教,在艾尔又一次沦陷之后指挥着星灵的最后一艘方舟舰:亚顿之矛。作为艾尔星灵数千年来的智慧结晶,亚顿之…...
centos安装gitlab
更新系统 sudo yum -y update安装所需要的包 sudo yum -y install epel-release curl vim policycoreutils-python如果要安装并使用本地Postfix服务器发送通知,请安装Postfix,这里就不安装了: sudo yum -y install postfix安装后启动并启用…...
)
【洛谷 P1093】[NOIP2007 普及组] 奖学金 题解(结构体排序)
[NOIP2007 普及组] 奖学金 题目描述 某小学最近得到了一笔赞助,打算拿出其中一部分为学习成绩优秀的前 555 名学生发奖学金。期末,每个学生都有 333 门课的成绩:语文、数学、英语。先按总分从高到低排序,如果两个同学总分相同,再…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
