【华为OD题库-055】金字塔/微商-java
题目
微商模式比较典型,下级每赚100元就要上交15元,给出每个级别的收入,求出金字塔尖上的人收入。
输入描述
第一行输入N,表示有N个代理商上下级关系
接下来输入N行,每行三个数:代理商代号 上级代理商代号 代理商赚的钱
输出描述
输出一行,两个以空格分隔的整数,含义如下: 金字塔顶代理商 最终的钱数
示例1:
输入
3
1 0 223
2 0 323
3 2 1203
输出
0 105
说明
2的最终收入等于323+1203/10015=323+ 180
0的最终收入等于(323+ 180 + 223)/10015= 105
示例2:
输入
4
1 0 100
2 0 200
3 0 300
4 0 200
输出
0 120
思路
题目未说明0一定就是顶级代理商,代理商之间的层级关系和编号大小无任何 关系。
使用两个map存放信息:
Map<Integer, List< Integer>> proxyBusiness 存放代理商关系,key存代理商id,val存下线集合
Map<Integer,Integer> pricesMap=new HashMap<>() 存每个代理商自己赚的钱
首先我们需要找到顶级代理商,在所有代理商中,如果该代理商自己没有赚钱,那么就是顶级代理商因为题目明确说了,只能输出一行,且每行三个数的含义是:代理商代号 上级代理商代号 代理商赚的钱),如果顶级代理商要赚钱,假定其编号是4,那么其输入格式必然是:4 ? x,没有上级代理商,所以无法处理?号输入什么。因此,本文解题逻辑就是输入中不会输入顶级代理商自己赚的钱。
如果要处理含顶级代理商自己赚的钱的信息,可以假想输入是:4 4 x的格式,此时判断顶级代理商的逻辑可以考虑成:将输入第一列放入子代理商集合,输入第二列放入父代理商集合。遍历所有父代理商,如果其没有出现在子代理商的集合中,那么其是顶级代理商。然后设计dfs递归函数:dfs(root),root代表传入的代理商编号,返回的值代表该代理商能够赚的钱
如果root没有子代理商,那么返回其自己赚的钱即可
如果有子代理商,遍历其所有子代理商,累加子代理商赚的钱sum
最后返回该代理商自己赚的钱+sum/100*50即可
题解
package hwod;import java.util.*;public class MicroBusiness {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = Integer.parseInt(sc.nextLine());int[][] nums = new int[n][3];for (int i = 0; i < n; i++) {nums[i] = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();}int[] res = microBusiness(nums);System.out.println(res[0] + " " + res[1]);}private static Map<Integer, List<Integer>> proxyBusiness = new HashMap<>(); //存关系private static Map<Integer,Integer> pricesMap=new HashMap<>(); //每个代理商赚的钱private static int[] microBusiness(int[][] nums) {Set<Integer> set = new HashSet<>();//存放有哪些代理商for (int i = 0; i < nums.length; i++) {List<Integer> oldChild = proxyBusiness.getOrDefault(nums[i][1], new ArrayList<>());oldChild.add(nums[i][0]);proxyBusiness.put(nums[i][1], oldChild);pricesMap.put(nums[i][0], nums[i][2]);set.add(nums[i][1]);set.add(nums[i][0]);}int root = -1;//寻找顶级代理商,自己不赚钱的代理商for (Integer proxy : set) {if (!pricesMap.containsKey(proxy)) {root = proxy;break;}}int res=dfs(root);return new int[]{root,res};}private static int dfs(int root) {if(!proxyBusiness.containsKey(root)) return pricesMap.getOrDefault(root,0);List<Integer> subList = proxyBusiness.get(root);int sum = 0;for (int i = 0; i < subList.size(); i++) {Integer sub = subList.get(i);sum += dfs(sub);}return pricesMap.getOrDefault(root,0)+sum / 100 * 15;}
}推荐
如果你对本系列的其他题目感兴趣,可以参考华为OD机试真题及题解(JAVA),查看当前专栏更新的所有题目。
相关文章:

【华为OD题库-055】金字塔/微商-java
题目 微商模式比较典型,下级每赚100元就要上交15元,给出每个级别的收入,求出金字塔尖上的人收入。 输入描述 第一行输入N,表示有N个代理商上下级关系 接下来输入N行,每行三个数:代理商代号 上级代理商代号 代理商赚的钱…...
OpenVINO异步Stable Diffusion推理优化方案
文章目录 Stable Diffusion 推理优化背景技术讲解:异步优化方案思路:异步推理优化原理OpenVINO异步推理Python API同步和异步实现方式对比 oneflow分布式调度优化优势:实现思路 总结: Stable Diffusion 推理优化 背景 2022年&…...

51单片机的智能加湿器控制系统【含proteus仿真+程序+报告+原理图】
1、主要功能 该系统由AT89C51单片机LCD1602显示模块DHT11湿度传感器模块继电器等模块构成。主要适用于智能自动加湿器、湿度保持、湿度控制等相似项目。 可实现基本功能: 1、LCD1602液晶屏实时显示湿度信息 2、DHT11采集湿度 3、按键可以调节适宜人体湿度的阈值范围࿰…...
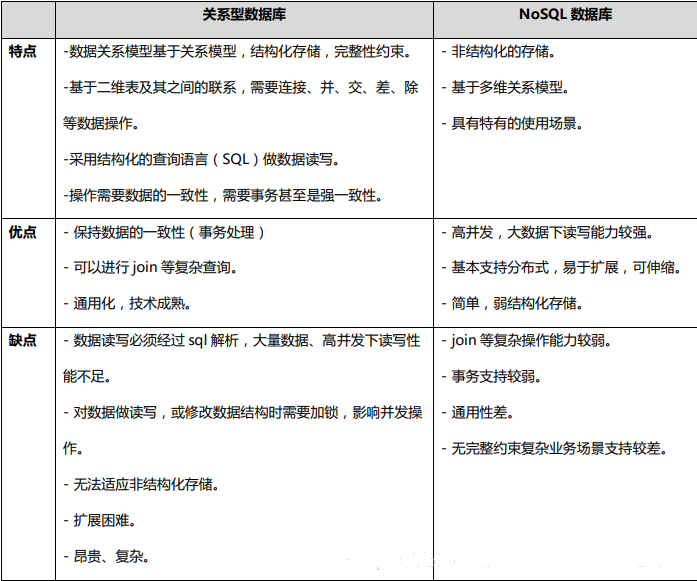
NoSql非关系型数据库
前言:Nosql not only sql,意即“不仅仅是sql”,泛指非关系型数据库。这些类型的数据存储不需要固定的模式(当然也有固定的模式),无需多余的操作就可以横向扩展。NoSql数据库中的数据是使用聚合模型来进行处…...
抖音集团面试挂在2面,复盘后,决定二战.....
先说下我基本情况,本科不是计算机专业,现在是学通信,然后做图像处理,可能面试官看我不是科班出身没有问太多计算机相关的问题,因为第一次找工作,字节的游戏专场又是最早开始的,就投递了…...

每个.NET开发都应掌握的C#处理文件系统I/O知识点
上篇文章讲述了C#多线程知识点,本文将介绍C#处理文件的知识点。在.NET开发领域,文件系统I/O是一个至关重要的主题,尤其是在处理文件、目录和数据存储方面。C#作为.NET平台的主要编程语言,提供了丰富而强大的文件系统I/O功能&#…...

vue3 中使用 sse 最佳实践,封装工具
工具 // 接受参数 export interface SSEChatParams {url: string,// sse 连接onmessage: (event: MessageEvent) > void,// 处理消息的函数onopen: () > void,// 建立连接触发的事件finallyHandler: () > void,// 相当于 try_finally 中的 finally 部分,不…...

OpenCV快速入门【完结】:总目录——初窥计算机视觉
文章目录 前言目录1. OpenCV快速入门:初探2. OpenCV快速入门:像素操作和图像变换3. OpenCV快速入门:绘制图形、图像金字塔和感兴趣区域4. OpenCV快速入门:图像滤波与边缘检测5. OpenCV快速入门:图像形态学操作6. OpenC…...
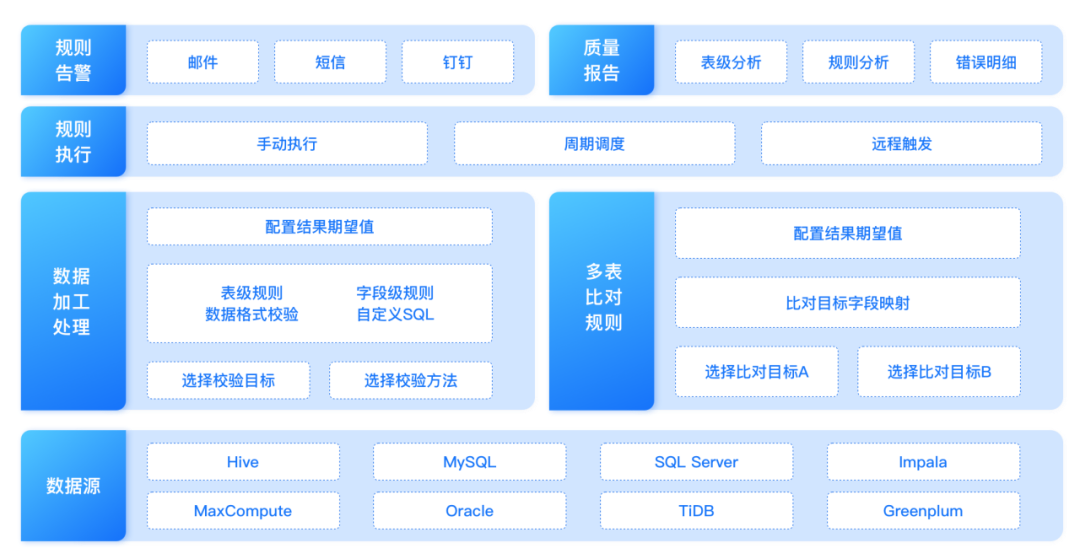
车企数据治理实践案例,实现数据生产、消费的闭环链路 | 数字化标杆
随着业务飞速发展,某汽车制造企业业务系统数量、复杂度和数据量都在呈几何级数的上涨,这就对于企业IT能力和IT架构模式的要求越来越高。加之企业大力发展数字化营销、新能源车等业务,希望通过持续优化客户体验,创造可持续发展的数…...
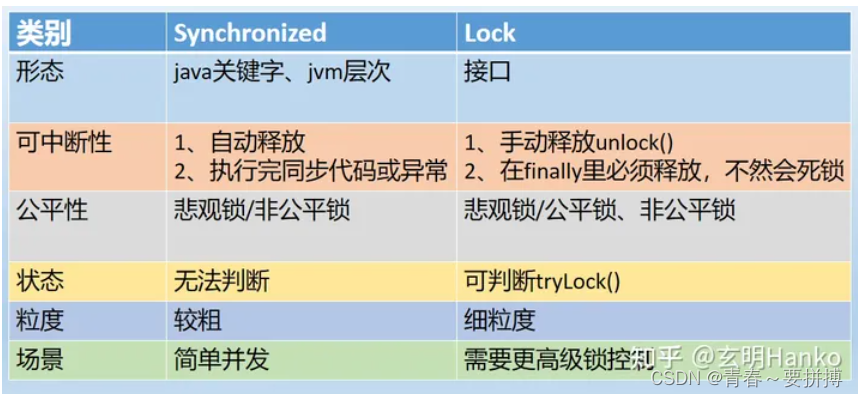
深入学习锁--Lock各种使用方法
一、什么是Lock Lock是一个接口,通常所说的可重入锁是指Lock的一个实现子类ReentrantLock 二、Lock实现步骤: ①创建锁对象Lock lock new ReentrantLock(); ②加锁lock.lock(); ③释放锁lock.unlock(); import java.util.concurrent.locks.Lock; import java.util…...
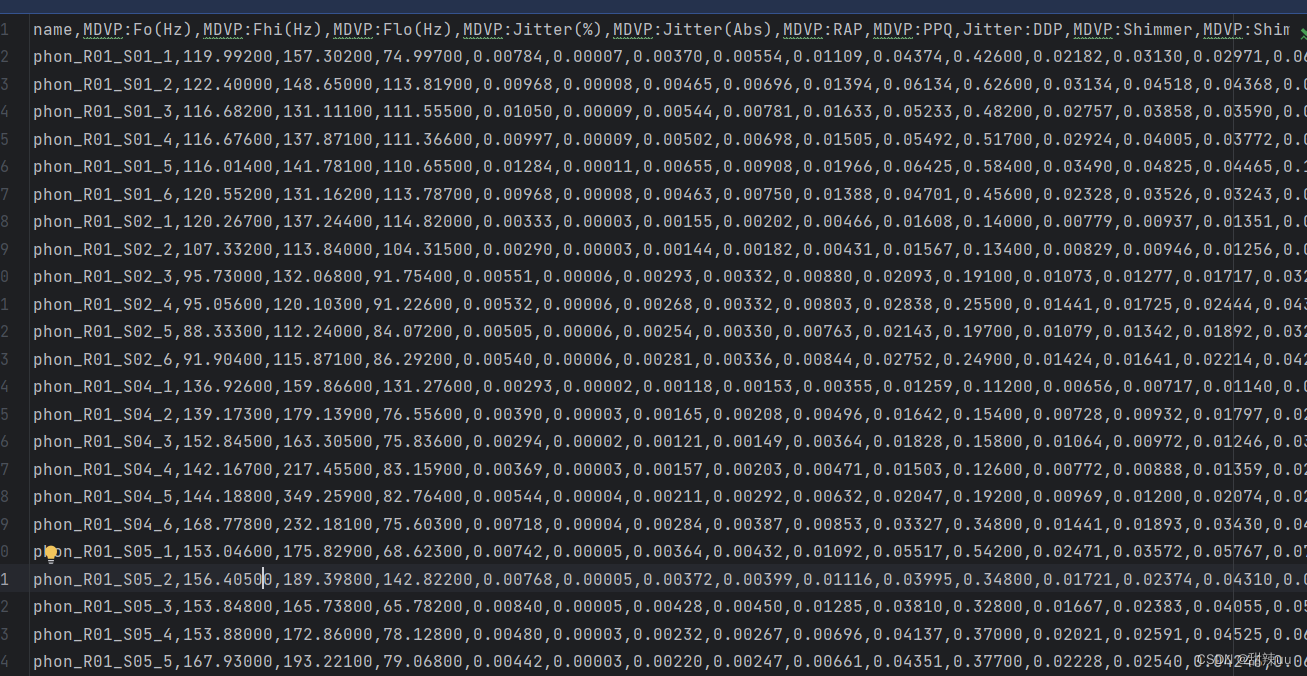
计算机毕设:基于机器学习的生物医学语音检测识别 附完整代码数据可直接运行
项目视频讲解: 基于机器学习的生物医学语音检测识别 完整代码数据可直接运行_哔哩哔哩_bilibili 运行效果图: 数据展示: 完整代码: #导入python的 numpy matplotlib pandas库 import pandas as pd import numpy as np import matplotlib.pyplot as plt #绘图 import se…...

VMware安装Ubuntu系统(Server端,Desktop端步骤一样)
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...
Navicat 与 华为云 GaussDB 合作再升级,赋能 GaussDB 分布式数据库
2023 年第三季度,Navicat 首次支持了华为云 GaussDB 主备版数据库。经过双方团队进一步的深化合作,Navicat 完成了 GaussDB 分布式的研发适配工作,赋能 GaussDB 全域数据库产品。 GaussDB 数据库分为主备版和分布式版两种模式。主备版适用于…...
【Docker】从零开始:13.Docker安装tomcat
Docker】从零开始:13.Docker安装Tomcat 下载Tomcat镜像启动Tomcat镜像新版本Tomcat修改访问Tomact首页 下载Tomcat镜像 [rootdocker ~]# docker pull tomcat Using default tag: latest latest: Pulling from library/tomcat 0e29546d541c: Pull complete 9b829c7…...
:Java 动态脚本)
风控规则引擎(一):Java 动态脚本
风控规则引擎(一):Java 动态脚本 日常场景 共享单车会根据微信分或者芝麻分来判断是否交押金汽车租赁公司也会根据微信分或者芝麻分来判断是否交押金在一些外卖 APP 都会提供根据你的信用等级来发放贷款产品金融 APP 中会根据很复杂规则来判…...

第五十六天|583. 两个字符串的删除操作 72. 编辑距离
583. 两个字符串的删除操作 可以求出最大子序列然后用字符串长度去减,也可以用删除的思路,如下: class Solution { public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size()1,vector<int…...

java中Lists.newArrayList和new ArrayList的详细区别?
下面是对Lists.newArrayList()和new ArrayList<>()的详细区别进行举例说明: 创建具有初始数据的列表: java Copy code import com.google.common.collect.Lists; List<String> list1 Lists.newArrayList("apple", "banana…...
从图片或PDF文件识别表格提取内容的简单库img2table
img2table是一个基于OpenCV 图像处理的用于 PDF 和图像的表识别和提取 Python库。由于其设计基于神经网络的解决方案,提供了一种实用且更轻便的替代方案,尤其是在 CPU 上使用时。 该库的特点: 识别图像和PDF文件中的表格,包括在表…...

CSV文件中使用insert 函数在指定列循环插入不同数据
文章目录 一、系统、工具要求二、需求三、代码实现:四、核心代码解读五、逐行更改某一列数据六:实现在文件的末尾增加指定内容列 一、系统、工具要求 pandaspythoncsv Windows 系统 二、需求 我有两个文件: 文件一:subject_ma…...
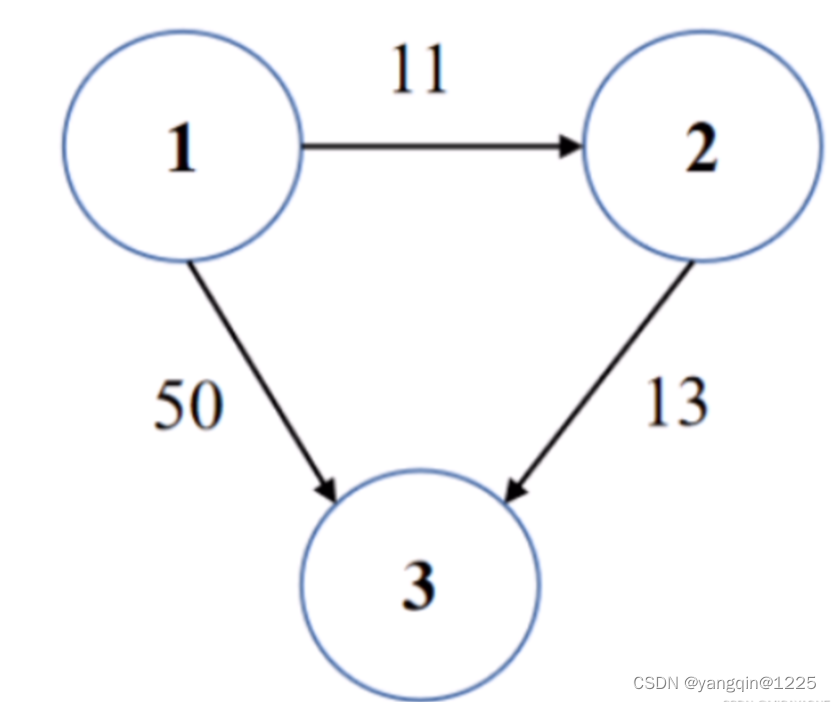
【华为OD题库-064】最小传输时延I-java
题目 某通信网络中有N个网络结点,用1到N进行标识。网络通过一个有向无环图.表示,其中图的边的值表示结点之间的消息传递时延。 现给定相连节点之间的时延列表times[]{u,v, w),其中u表示源结点,v表示目的结点࿰…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
